Bir jinsli chiziqli TENGLAMALAR TIZIMI
Bir hil tizim chiziqli tenglamalar shakl tizimi deb ataladi
Bu holatda bu aniq 
, chunki bu determinantlardagi ustunlardan birining barcha elementlari nolga teng.
Noma'lumlar formulalar bo'yicha topilganligi sababli 
, keyin D ≠ 0 bo'lganda, tizim yagona nol yechimga ega x = y = z= 0. Biroq, ko'p masalalarda qiziqarli savol bir hil tizim noldan boshqa yechimlar.
Teorema. Chiziqli tizim uchun bir jinsli tenglamalar nolga teng bo'lmagan yechimga ega bo'lsa, D ≠ 0 bo'lishi zarur va etarli.
Demak, agar determinant D ≠ 0 bo'lsa, u holda tizim yagona yechimga ega. Agar D ≠ 0 bo'lsa, u holda chiziqli bir jinsli tenglamalar tizimi cheksiz ko'p echimlarga ega.
Misollar.
Matritsaning xos vektorlari va xos qiymatlari
Kvadrat matritsa berilsin 
, X– balandligi matritsaning tartibiga to‘g‘ri keladigan ba’zi matritsa-ustun A. .
Ko'pgina masalalarda biz tenglamani ko'rib chiqishimiz kerak X
bu erda l - ma'lum bir raqam. Har qanday l uchun bu tenglama nol yechimga ega ekanligi aniq.
Bu tenglama nolga teng bo'lmagan yechimlarga ega bo'lgan l soni deyiladi xos qiymat matritsalar A, A X chunki bunday l deyiladi xos vektor matritsalar A.
Matritsaning xos vektorini topamiz A. Chunki E∙X = X, keyin matritsa tenglamasini quyidagicha qayta yozish mumkin 
yoki 
. Kengaytirilgan shaklda bu tenglama chiziqli tenglamalar tizimi sifatida qayta yozilishi mumkin. Haqiqatan ham 
.
Va shuning uchun 
Shunday qilib, biz koordinatalarni aniqlash uchun bir hil chiziqli tenglamalar tizimini oldik x 1, x 2, x 3 vektor X. Tizim nolga teng bo'lmagan yechimlarga ega bo'lishi uchun tizimning determinanti nolga teng bo'lishi zarur va etarli, ya'ni.
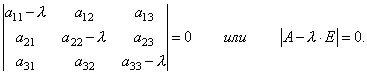
Bu l uchun 3-darajali tenglama. Bu deyiladi xarakterli tenglama matritsalar A va l ning xos qiymatlarini aniqlashga xizmat qiladi.
Har bir xos qiymat l xos vektorga mos keladi X, uning koordinatalari tizimdan l ning mos keladigan qiymatida aniqlanadi.
Misollar.
VEKTOR ALGEBRA. VEKTOR TUSHUNCHASI
Fizikaning turli bo'limlarini o'rganayotganda ularning son qiymatlarini ko'rsatish orqali to'liq aniqlanadigan miqdorlar mavjud, masalan, uzunlik, maydon, massa, harorat va boshqalar. Bunday miqdorlar skalyar deyiladi. Biroq, ularga qo'shimcha ravishda kattaliklar ham mavjud bo'lib, ularni aniqlash uchun sonli qiymatdan tashqari, ularning fazodagi yo'nalishini ham bilish kerak, masalan, tanaga ta'sir qiluvchi kuch, harakat tezligi va tezlanishi. kosmosda harakat qilganda tanasi, kuchlanish magnit maydon kosmosning ma'lum bir nuqtasida va boshqalar. Bunday kattaliklar vektor kattaliklar deyiladi.
Keling, qat'iy ta'rifni kiritaylik.
Yo'naltirilgan segment Uchlariga nisbatan qaysi biri birinchi, qaysi biri ikkinchi ekanligi ma'lum bo'lgan segmentni chaqiraylik.
Vektor ma'lum uzunlikka ega bo'lgan yo'naltirilgan segment deb ataladi, ya'ni. Bu ma'lum uzunlikdagi segment bo'lib, uni cheklovchi nuqtalardan biri boshi, ikkinchisi esa oxiri sifatida olinadi. Agar A- vektorning boshlanishi, B uning oxiri, keyin vektor qo'shimcha ravishda belgi bilan belgilanadi, vektor ko'pincha bitta harf bilan belgilanadi; Rasmda vektor segment bilan, yo'nalishi esa o'q bilan ko'rsatilgan.
Modul yoki uzunligi Vektor uni aniqlaydigan yo'naltirilgan segmentning uzunligi deb ataladi. || bilan belgilanadi yoki ||.
Biz, shuningdek, vektor sifatida boshlanishi va oxiri bir-biriga mos keladigan nol vektorni ham kiritamiz. Belgilangan. Nol vektor o'ziga xos yo'nalishga ega emas va uning moduli nolga teng ||=0.
Vektorlar deyiladi kollinear, agar ular bir chiziqda yoki parallel chiziqlarda joylashgan bo'lsa. Bundan tashqari, agar va vektorlari bir xil yo'nalishda bo'lsa, biz yozamiz , qarama-qarshi.
Xuddi shu tekislikka parallel bo'lgan to'g'ri chiziqlarda joylashgan vektorlar deyiladi koplanar.
Ikki vektor deyiladi teng, agar ular kollinear bo'lsa, bir xil yo'nalishga ega va uzunligi teng. Bunday holda ular yozadilar.
Vektorlar tengligining ta'rifidan kelib chiqadiki, vektorni fazoning istalgan nuqtasida o'ziga parallel ravishda ko'chirish mumkin.
Masalan.
VEKTORLARDA CHIZIQLI AMALIYATLAR
- Vektorni raqamga ko'paytirish.
Vektor va l sonining ko'paytmasi yangi vektor bo'lib, shundayki:
Vektor va l sonining ko'paytmasi bilan belgilanadi.
Masalan, vektor bilan bir xil yo'nalishda yo'naltirilgan va uzunligi vektorning yarmiga teng vektor mavjud.
Kiritilgan operatsiya quyidagilarga ega xususiyatlari:
- Vektor qo'shilishi.
Ikki ixtiyoriy vektor bo'lsin va bo'lsin. Keling, ixtiyoriy bir nuqtani olaylik O va vektorni tuzing. Shundan keyin nuqtadan A vektorni chetga surib qo'yamiz. Birinchi vektorning boshini ikkinchi vektorning oxiri bilan bog'lovchi vektor deyiladi miqdori bu vektorlardan va belgilanadi
.
Vektor qo'shishning tuzilgan ta'rifi deyiladi parallelogramma qoidasi, chunki vektorlarning bir xil yig'indisini quyidagicha olish mumkin. Keling, nuqtadan keyinga qoldiraylik O vektorlar va . Keling, bu vektorlarga parallelogramm quramiz OABC. Chunki vektorlar, keyin vektor, ya'ni cho'qqidan chizilgan parallelogrammaning diagonali O, vektorlar yig'indisi bo'lishi aniq.
Quyidagilarni tekshirish oson vektor qo'shish xossalari.
- Vektor farqi.
Uzunligi teng va qarama-qarshi yo'naltirilgan berilgan vektorga kollinear vektor deyiladi qarama-qarshi vektor uchun vektor va bilan belgilanadi. Qarama-qarshi vektor vektorni l = –1 soniga ko'paytirish natijasi sifatida qaralishi mumkin: .
Ta'rif 9.3. Vektor X chaqirdi xos vektor matritsalar A, agar shunday raqam mavjud bo'lsa λ, tenglik amal qiladi: A X= λ X, ya'ni murojaat qilish natijasi X matritsa tomonidan belgilangan chiziqli transformatsiya A, bu vektorni songa ko'paytirish λ . Raqamning o'zi λ chaqirdi xos qiymat matritsalar A.
Formulalarga almashtirish (9.3) x` j = lx j, xos vektorning koordinatalarini aniqlash uchun tenglamalar tizimini olamiz:
. (9.5)
Bu chiziqli bir jinsli sistema faqat uning asosiy determinanti 0 (Kramer qoidasi) bo'lsagina notrivial yechimga ega bo'ladi. Ushbu shartni quyidagi shaklda yozish orqali:
xos qiymatlarni aniqlash uchun tenglamani olamiz λ , chaqirildi xarakterli tenglama. Qisqacha aytganda, uni quyidagicha ifodalash mumkin:
| A - lE | = 0, (9.6)
chunki uning chap tomonida matritsaning determinanti mavjud A-lE. Polinom nisbiy l | A - lE| chaqirdi xarakterli polinom matritsalar A.
Xarakteristik polinomning xossalari:
1) Chiziqli transformatsiyaning xarakterli ko'phadlari bazis tanlashga bog'liq emas. Isbot. 
(qarang (9.4)), lekin 
demak, . Shunday qilib, bu asosni tanlashga bog'liq emas. Bu shuni anglatadiki | A-lE| yangi asosga o'tishda o'zgarmaydi.
2) Agar matritsa A chiziqli transformatsiya hisoblanadi simmetrik(bular. va ij =a ji), u holda (9.6) xarakteristik tenglamaning barcha ildizlari haqiqiy sonlardir.
Xususiy qiymatlar va xos vektorlarning xususiyatlari:
1) Agar siz xos vektorlardan asos tanlasangiz x 1, x 2, x 3 , xos qiymatlarga mos keladi l 1, l 2, l 3 matritsalar A, u holda bu asosda chiziqli transformatsiya A diagonal shakldagi matritsaga ega:
(9.7) Bu xossaning isboti xos vektorlarning ta’rifidan kelib chiqadi.
2) Agar transformatsiyaning xos qiymatlari bo'lsa A har xil bo'lsa, ularning tegishli xos vektorlari chiziqli mustaqil bo'ladi.
3) Agar matritsaning xarakteristik polinomi A uchtasi bor turli xil ildizlar, keyin qandaydir asosda matritsa A diagonal ko'rinishga ega.
Keling, matritsaning xos qiymatlari va xos vektorlarini topamiz. xarakterli tenglama: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7 λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
Har bir topilgan qiymatga mos keladigan xos vektorlarning koordinatalarini topamiz λ. (9.5) dan kelib chiqadiki, agar X (1) ={x 1 , x 2 , x 3) – mos keladigan xos vektor λ 1 = -2, keyin
- kooperativ, ammo noaniq tizim. Uning yechimi shaklda yozilishi mumkin X (1)
={a,0,-a), bu erda a har qanday raqam. Xususan, shuni talab qilsak | x (1)
|=1, X (1)
=
Tizimga almashtirish (9.5) λ 2 =3, ikkinchi xos vektorning koordinatalarini aniqlash sistemasini olamiz - x (2) ={y 1 , y 2 , y 3}:
, qayerda X (2)
={b,-b,b) yoki, taqdim | x (2)
|=1, x (2)
= 
Uchun λ 3 = 6 xos vektorni toping x (3) ={z 1 , z 2 , z 3}:
, x (3)
={c,2c, c) yoki normallashtirilgan versiyada
x (3) = 
Shuni ta'kidlash mumkin X (1) X (2)
= ab–ab= 0, x (1) x (3)
= ac-ac= 0, x (2) x (3)
= miloddan avvalgi- 2miloddan avvalgi + miloddan avvalgi= 0. Shunday qilib, bu matritsaning xos vektorlari juft ortogonaldir.
10-ma'ruza.
Kvadrat shakllar va ularning simmetrik matritsalar bilan aloqasi. Simmetrik matritsaning xos vektorlari va xos qiymatlari. Kvadrat shaklni kanonik shaklga keltirish.
Ta'rif 10.1.Kvadrat shakli haqiqiy o'zgaruvchilar x 1, x 2,…, x n bu oʻzgaruvchilarda birinchi darajali erkin had va hadlarni oʻz ichiga olmagan ikkinchi darajali koʻphad deyiladi.
Kvadrat shakllarga misollar:
(n = 2),
(n = 3). (10.1)
Oxirgi ma'ruzada berilgan simmetrik matritsaning ta'rifini eslaylik:
Ta'rif 10.2. Kvadrat matritsa deyiladi simmetrik, agar , ya'ni asosiy diagonalga nisbatan simmetrik bo'lgan matritsa elementlari teng bo'lsa.
Simmetrik matritsaning xos qiymatlari va xos vektorlarining xossalari:
1) Simmetrik matritsaning barcha xos qiymatlari haqiqiydir.
Isbot (uchun n = 2).
Matritsa bo'lsin A shaklga ega: 
. Xarakteristik tenglama tuzamiz:
(10.2) Diskriminantni topamiz:
Shuning uchun tenglama faqat haqiqiy ildizlarga ega.
2) Xususiy vektorlar simmetrik matritsalar ortogonaldir.
Isbot (uchun n= 2).
Xususiy vektorlarning koordinatalari va tenglamalarni qanoatlantirishi kerak.
www.sayt topishga imkon beradi. Sayt hisob-kitoblarni amalga oshiradi. Bir necha soniya ichida server to'g'ri echimni beradi. Matritsa uchun xarakteristik tenglama bo'ladi algebraik ifoda, determinantni hisoblash qoidasi bilan topiladi matritsalar matritsalar, asosiy diagonal bo'ylab diagonal elementlar va o'zgaruvchining qiymatlarida farqlar bo'ladi. Hisoblashda matritsa uchun xarakterli tenglama onlayn, har bir element matritsalar mos keladigan boshqa elementlar bilan ko'paytiriladi matritsalar. Rejimda toping onlayn faqat kvadrat uchun mumkin matritsalar. Topish operatsiyasi matritsa uchun xarakterli tenglama onlayn elementlar ko'paytmasining algebraik yig'indisini hisoblashga qisqartiradi matritsalar determinantni topish natijasida matritsalar, faqat aniqlash maqsadida matritsa uchun xarakterli tenglama onlayn. Bu operatsiya nazariyasida alohida o‘rin tutadi matritsalar, ildizlar yordamida xos qiymatlar va vektorlarni topishga imkon beradi. Topish vazifasi matritsa uchun xarakterli tenglama onlayn ko'paytiruvchi elementlardan iborat matritsalar keyin bu mahsulotlarni ma'lum bir qoida bo'yicha jamlash. www.sayt topadi matritsa uchun xarakteristik tenglama rejimida berilgan o'lcham onlayn. Hisoblash matritsa uchun xarakterli tenglama onlayn uning o'lchamini hisobga olgan holda, bu determinantni hisoblash qoidasiga ko'ra topilgan raqamli yoki ramziy koeffitsientli ko'phadni topishdir. matritsalar- mos elementlarning mahsuloti yig'indisi sifatida matritsalar, faqat aniqlash maqsadida matritsa uchun xarakterli tenglama onlayn. Kvadrat uchun o'zgaruvchiga nisbatan ko'phadni topish matritsalar, ta'rif sifatida matritsa uchun xarakteristik tenglama, nazariy jihatdan keng tarqalgan matritsalar. Ko'phadning ildizlarining ma'nosi matritsa uchun xarakterli tenglama onlayn uchun xos vektorlar va xos qiymatlarni aniqlash uchun ishlatiladi matritsalar. Bundan tashqari, agar determinant bo'lsa matritsalar u holda nolga teng bo'ladi matritsaning xarakteristik tenglamasi teskarisidan farqli o'laroq, hali ham mavjud bo'ladi matritsalar. Hisoblash uchun matritsa uchun xarakteristik tenglama yoki bir vaqtning o'zida bir nechtasini toping matritsalarning xarakteristik tenglamalari, siz ko'p vaqt va kuch sarflashingiz kerak, bizning serverimiz bir necha soniya ichida topadi matritsa uchun xarakterli tenglama onlayn. Bu holda, topish uchun javob matritsa uchun xarakterli tenglama onlayn topishda raqamlar bo'lsa ham, to'g'ri va etarli aniqlik bilan bo'ladi matritsa uchun xarakterli tenglama onlayn mantiqsiz bo'ladi. Saytda www.sayt elementlarda belgilar kiritishga ruxsat beriladi matritsalar, ya'ni matritsa uchun xarakterli tenglama onlayn hisoblashda umumiy ramziy shaklda ifodalanishi mumkin matritsaning xarakteristik tenglamasi onlayn. Topish masalasini yechishda olingan javobni tekshirish foydalidir matritsa uchun xarakterli tenglama onlayn saytdan foydalanish www.sayt. Polinomni hisoblash operatsiyasini bajarishda - matritsaning xarakteristik tenglamasi, bu muammoni hal qilishda ehtiyotkor va o'ta diqqatli bo'lishingiz kerak. O'z navbatida, bizning saytimiz mavzu bo'yicha qaroringizni tekshirishga yordam beradi matritsaning xarakterli tenglamasi onlayn. Agar hal qilingan muammolarni uzoq vaqt tekshirishga vaqtingiz bo'lmasa, unda www.sayt topish va hisoblashda tekshirish uchun qulay vosita bo'lishi shubhasiz matritsa uchun xarakterli tenglama onlayn.
Kvadrat matritsaning xos vektori berilgan matritsaga ko'paytirilganda kollinear vektor hosil bo'ladi. Oddiy so'zlar bilan aytganda, matritsani xos vektor bilan ko'paytirishda, ikkinchisi bir xil bo'lib qoladi, lekin ma'lum bir songa ko'paytiriladi.
Ta'rif
Xususiy vektor nolga teng bo'lmagan V vektor bo'lib, u M kvadrat matritsaga ko'paytirilganda o'zini qandaydir l soniga ortib boradi. Algebraik yozuvda u quyidagicha ko'rinadi:
M × V = l × V,
bu yerda l - M matritsaning xos qiymati.
Keling, ko'rib chiqaylik raqamli misol. Yozib olish qulayligi uchun matritsadagi raqamlar nuqtali vergul bilan ajratiladi. Keling, matritsaga ega bo'lamiz:
- M = 0; 4;
- 6; 10.
Uni ustun vektoriga ko'paytiramiz:
- V = -2;
Matritsani ustun vektoriga ko'paytirsak, biz ustun vektorini ham olamiz. Qattiq matematik til 2 × 2 matritsani ustun vektoriga ko'paytirish formulasi quyidagicha ko'rinadi:
- M × V = M11 × V11 + M12 × V21;
- M21 × V11 + M22 × V21.
M11 birinchi qator va birinchi ustunda joylashgan M matritsasining elementini, M22 esa ikkinchi qator va ikkinchi ustunda joylashgan elementni bildiradi. Bizning matritsamiz uchun bu elementlar M11 = 0, M12 = 4, M21 = 6, M22 10 ga teng. Ustun vektori uchun bu qiymatlar V11 = –2, V21 = 1 ga teng. Ushbu formulaga muvofiq, kvadrat matritsaning vektor bo'yicha ko'paytmasining quyidagi natijasini olamiz:
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
Qulaylik uchun ustun vektorini qatorga yozamiz. Shunday qilib, kvadrat matritsani vektorga (-2; 1) ko'paytirdik, natijada vektor (4; -2) hosil bo'ldi. Shubhasiz, bu bir xil vektor l = -2 ga ko'paytiriladi. Lambda ichida Ushbu holatda matritsaning xos qiymatini bildiradi.
Matritsaning xos vektori bu kollinear vektor, ya'ni matritsaga ko'paytirilganda fazodagi o'rnini o'zgartirmaydigan ob'ekt. Vektor algebrasida kollinearlik tushunchasi geometriyadagi parallellik atamasiga o'xshaydi. Geometrik talqinda kollinear vektorlar turli uzunlikdagi parallel yo'naltirilgan segmentlardir. Evklid davridan beri biz bir chiziqda unga parallel cheksiz sonli chiziqlar borligini bilamiz, shuning uchun har bir matritsaning cheksiz sonli xos vektorlari bor deb taxmin qilish mantiqan to'g'ri keladi.
Oldingi misoldan ko'rinib turibdiki, xos vektorlar (-8; 4) va (16; -8) va (32, -16) bo'lishi mumkin. Bularning barchasi l = -2 xos qiymatga mos keladigan kollinear vektorlardir. Asl matritsani ushbu vektorlarga ko'paytirganda, biz hali ham asl nusxadan 2 marta farq qiladigan vektorga ega bo'lamiz. Shuning uchun xos vektorni topish masalalarini yechishda faqat chiziqli mustaqil vektor ob'ektlarni topish kerak bo'ladi. Ko'pincha, n × n matritsa uchun n ta sonli xos vektorlar mavjud. Bizning kalkulyatorimiz ikkinchi tartibli kvadrat matritsalarni tahlil qilish uchun mo'ljallangan, shuning uchun deyarli har doim natija ikkita xos vektorni topadi, ular bir-biriga to'g'ri keladigan holatlar bundan mustasno.
Yuqoridagi misolda biz dastlabki matritsaning xos vektorini oldindan bilib oldik va lambda sonini aniq belgilab oldik. Biroq, amalda hamma narsa aksincha sodir bo'ladi: birinchi navbatda xos qiymatlar va faqat keyin xos vektorlar topiladi.
Yechim algoritmi
Keling, M matritsasini yana ko'rib chiqamiz va uning ikkala xos vektorini topishga harakat qilamiz. Shunday qilib, matritsa quyidagicha ko'rinadi:
- M = 0; 4;
- 6; 10.
Avval biz l ning xos qiymatini aniqlashimiz kerak, bu quyidagi matritsaning determinantini hisoblashni talab qiladi:
- (0 - l); 4;
- 6; (10 − l).
Ushbu matritsa asosiy diagonaldagi elementlardan noma'lum l ni ayirish yo'li bilan olinadi. Determinant standart formula yordamida aniqlanadi:
- detA = M11 × M21 - M12 × M22
- detA = (0 - l) × (10 - l) - 24
Bizning vektorimiz nolga teng bo'lmasligi kerakligi sababli, hosil bo'lgan tenglamani chiziqli bog'liq deb qabul qilamiz va detA determinantimizni nolga tenglashtiramiz.
(0 - l) × (10 - l) - 24 = 0
Qavslarni ochamiz va matritsaning xarakteristik tenglamasini olamiz:
l 2 - 10l - 24 = 0
Bu standart kvadrat tenglama, bu diskriminant orqali hal qilinishi kerak.
D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196
Diskriminantning ildizi sqrt(D) = 14, shuning uchun l1 = -2, l2 = 12. Endi har bir lambda qiymati uchun xos vektorni topishimiz kerak. l = -2 uchun tizim koeffitsientlarini ifodalaymiz.
- M - l × E = 2; 4;
- 6; 12.
Bu formulada E identifikatsiya matritsasi hisoblanadi. Olingan matritsaga asoslanib, chiziqli tenglamalar tizimini yaratamiz:
2x + 4y = 6x + 12y,
bu yerda x va y xos vektor elementlari.
Keling, chapdagi barcha X ni va o'ngdagi barcha Y ni to'playmiz. Shubhasiz - 4x = 8y. Ifodani - 4 ga bo'ling va x = -2y ni oling. Endi biz noma'lumlarning har qanday qiymatlarini olib, matritsaning birinchi xos vektorini aniqlashimiz mumkin (chiziqli bog'liq xos vektorlarning cheksizligini eslang). y = 1, keyin x = –2 ni olaylik. Shuning uchun birinchi xos vektor V1 = (–2; 1) ga o'xshaydi. Maqolaning boshiga qayting. Aynan shu vektor ob'ekti bo'lib, biz xos vektor tushunchasini ko'rsatish uchun matritsani ko'paytirdik.
Endi l = 12 uchun xos vektorni topamiz.
- M - l × E = -12; 4
- 6; -2.
Bir xil chiziqli tenglamalar tizimini tuzamiz;
- -12x + 4y = 6x - 2y
- -18x = -6y
- 3x = y.
Endi biz x = 1 ni olamiz, shuning uchun y = 3. Shunday qilib, ikkinchi xos vektor V2 = (1; 3) ga o'xshaydi. Asl matritsani berilgan vektorga ko'paytirishda natija har doim bir xil vektor 12 ga ko'paytiriladi. Bu erda yechim algoritmi tugaydi. Endi siz matritsaning xos vektorini qo'lda qanday aniqlashni bilasiz.
- aniqlovchi;
- iz, ya'ni asosiy diagonaldagi elementlar yig'indisi;
- daraja, ya'ni chiziqli mustaqil satrlar/ustunlarning maksimal soni.
Dastur yuqoridagi algoritmga muvofiq ishlaydi, yechim jarayonini imkon qadar qisqartiradi. Shuni ta'kidlash kerakki, dasturda lambda "c" harfi bilan belgilanadi. Keling, raqamli misolni ko'rib chiqaylik.
Dastur qanday ishlashiga misol
Keling, quyidagi matritsa uchun xos vektorlarni aniqlashga harakat qilaylik:
- M = 5; 13;
- 4; 14.
Keling, ushbu qiymatlarni kalkulyatorning katakchalariga kiritamiz va javobni quyidagi shaklda olamiz:
- Matritsa darajasi: 2;
- Matritsa determinanti: 18;
- Matritsa izi: 19;
- Xususiy vektorni hisoblash: c 2 - 19.00c + 18.00 (xarakteristik tenglama);
- Eigenvektorni hisoblash: 18 (birinchi lambda qiymati);
- Eigenvektorni hisoblash: 1 (ikkinchi lambda qiymati);
- 1-vektor uchun tenglamalar tizimi: -13x1 + 13y1 = 4x1 − 4y1;
- 2-vektor uchun tenglamalar tizimi: 4x1 + 13y1 = 4x1 + 13y1;
- Xususiy vektor 1: (1; 1);
- 2 xos vektor: (-3,25; 1).
Shunday qilib, biz ikkita chiziqli mustaqil xususiy vektorni oldik.
Xulosa
Chiziqli algebra va analitik geometriya har qanday birinchi kurs muhandislik mutaxassisligi uchun standart fanlardir. Vektorlar va matritsalarning ko'pligi dahshatli va bunday noqulay hisob-kitoblarda xato qilish oson. Bizning dasturimiz talabalarga o'z hisoblarini tekshirish yoki xos vektorni topish masalasini avtomatik ravishda hal qilish imkonini beradi. Bizning katalogimizda boshqa chiziqli algebra kalkulyatorlari mavjud.
