Un número que representa un decimal. Notación decimal de un número fraccionario

En este tutorial veremos cada una de estas operaciones por separado.

Contenido de la lección

Sumar decimales

Como sabemos, una fracción decimal tiene una parte entera y una parte fraccionaria. Al sumar decimales, las partes enteras y fraccionarias se suman por separado.

Por ejemplo, sumemos las fracciones decimales 3,2 y 5,3. Es más conveniente sumar fracciones decimales en una columna.

Primero escribamos estas dos fracciones en una columna, con las partes enteras necesariamente debajo de los números enteros y las fracciones debajo de las fracciones. En la escuela este requisito se llama "coma debajo de coma".

Escribamos las fracciones en una columna de modo que la coma quede debajo de la coma:

Empezamos a sumar las partes fraccionarias: 2 + 3 = 5. Escribimos el cinco en la parte fraccionaria de nuestra respuesta:

Ahora sumamos las partes enteras: 3 + 5 = 8. Escribimos un ocho en la parte entera de nuestra respuesta:

Ahora separamos la parte entera de la fraccionaria con una coma. Para hacer esto, volvemos a seguir la regla. "coma debajo de coma":

Recibimos una respuesta de 8,5. Entonces la expresión 3,2 + 5,3 es igual a 8,5

De hecho, no todo es tan sencillo como parece a primera vista. Aquí también hay trampas, de las que hablaremos ahora.

Lugares en decimales

Las fracciones decimales, al igual que los números ordinarios, tienen sus propios dígitos. Estos son lugares de décimas, lugares de centésimas, lugares de milésimas. En este caso, los dígitos comienzan después del punto decimal.

El primer dígito después del punto decimal es responsable del lugar de las décimas, el segundo dígito después del punto decimal de las centésimas y el tercer dígito después del punto decimal de las milésimas.

Los lugares en fracciones decimales contienen algunos información útil. Específicamente, te dicen cuántas décimas, centésimas y milésimas hay en un decimal.

Por ejemplo, considere la fracción decimal 0,345.

La posición donde se ubica el tres se llama décimo lugar

La posición donde se ubica el cuatro se llama lugar de las centésimas

La posición donde se ubica el cinco se llama milésimo lugar

Miremos este dibujo. Vemos que hay un tres en el lugar de las décimas. Esto nos dice que hay tres décimas en la fracción decimal 0,345.

Si sumamos las fracciones, obtenemos la fracción decimal original 0,345

Se puede ver que al principio recibimos la respuesta, pero la convertimos a una fracción decimal y obtuvimos 0,345.

Al sumar fracciones decimales, se siguen los mismos principios y reglas que al sumar números ordinarios. La suma de fracciones decimales se produce en dígitos: las décimas se suman a las décimas, las centésimas a las centésimas y las milésimas a las milésimas.

Por lo tanto, al sumar fracciones decimales, debes seguir la regla "coma debajo de coma". La coma debajo de la coma proporciona el orden mismo en el que se suman décimas a décimas, centésimas a centésimas, milésimas a milésimas.

Ejemplo 1. Encuentra el valor de la expresión 1,5 + 3,4.

Primero que nada, sumamos las partes fraccionarias 5 + 4 = 9. Escribimos nueve en la parte fraccionaria de nuestra respuesta:

Ahora sumamos las partes enteras 1 + 3 = 4. Escribimos el cuatro en la parte entera de nuestra respuesta:

Ahora separamos la parte entera de la fraccionaria con una coma. Para hacer esto, volvemos a seguir la regla de “coma debajo de coma”:

Recibimos una respuesta de 4,9. Esto significa que el valor de la expresión 1,5 + 3,4 es 4,9

Ejemplo 2. Encuentra el valor de la expresión: 3,51 + 1,22

Escribimos esta expresión en una columna, observando la regla de “coma debajo de coma”.

En primer lugar, sumamos la parte fraccionaria, es decir, las centésimas de 1+2=3. Escribimos un triple en la centésima parte de nuestra respuesta:

Ahora suma las décimas 5+2=7. Escribimos un siete en la décima parte de nuestra respuesta:

Ahora sumamos las partes enteras 3+1=4. Escribimos los cuatro en toda la parte de nuestra respuesta:

Separamos la parte entera de la fraccionaria con una coma, observando la regla “coma bajo coma”:

La respuesta que recibimos fue 4,73. Esto significa que el valor de la expresión 3,51 + 1,22 es igual a 4,73

3,51 + 1,22 = 4,73

Al igual que con los números normales, al sumar decimales, . En este caso, se escribe un dígito en la respuesta y el resto se transfiere al siguiente dígito.

Ejemplo 3. Encuentra el valor de la expresión 2,65 + 3,27.

Escribimos esta expresión en la columna:

Suma las centésimas partes 5+7=12. El número 12 no cabe en la centésima parte de nuestra respuesta. Por tanto, en la centésima parte escribimos el número 2, y trasladamos la unidad al siguiente dígito:

Ahora sumamos las décimas de 6 + 2 = 8 más la unidad que obtuvimos de la operación anterior, obtenemos 9. Escribimos el número 9 en la décima de nuestra respuesta:

Ahora sumamos las partes enteras 2+3=5. Escribimos el número 5 en la parte entera de nuestra respuesta:

Recibimos una respuesta de 5,92. Esto significa que el valor de la expresión 2,65 + 3,27 es igual a 5,92

2,65 + 3,27 = 5,92

Ejemplo 4. Encuentra el valor de la expresión 9,5 + 2,8.

Escribimos esta expresión en la columna.

Sumamos las partes fraccionarias 5 + 8 = 13. El número 13 no encajará en la parte fraccionaria de nuestra respuesta, por lo que primero escribimos el número 3 y movemos la unidad al siguiente dígito, o mejor dicho, lo transferimos al parte entera:

Ahora sumamos las partes enteras 9+2=11 más la unidad que obtuvimos de la operación anterior, obtenemos 12. Escribimos el número 12 en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Recibimos la respuesta 12.3. Esto significa que el valor de la expresión 9,5 + 2,8 es 12,3

9,5 + 2,8 = 12,3

Al sumar decimales, el número de dígitos después del punto decimal en ambas fracciones debe ser el mismo. Si no hay suficientes números, estos lugares en la parte fraccionaria se rellenan con ceros.

Ejemplo 5. Encuentra el valor de la expresión: 12,725 + 1,7

Antes de escribir esta expresión en una columna, hagamos que el número de dígitos después del punto decimal en ambas fracciones sea el mismo. La fracción decimal 12,725 tiene tres dígitos después del punto decimal, pero la fracción 1,7 tiene solo uno. Esto significa que en la fracción 1.7 debes agregar dos ceros al final. Luego obtenemos la fracción 1.700. Ahora puedes escribir esta expresión en una columna y comenzar a calcular:

Suma las milésimas partes 5+0=5. Escribimos el número 5 en la milésima parte de nuestra respuesta:

Suma las centésimas partes 2+0=2. Escribimos el número 2 en la centésima parte de nuestra respuesta:

Suma las décimas 7+7=14. El número 14 no cabe en una décima parte de nuestra respuesta. Por lo tanto, primero escribimos el número 4 y pasamos la unidad al siguiente dígito:

Ahora sumamos las partes enteras 12+1=13 más la unidad que obtuvimos de la operación anterior, obtenemos 14. Escribimos el número 14 en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Recibimos una respuesta de 14.425. Esto significa que el valor de la expresión 12.725+1.700 es 14.425

12,725+ 1,700 = 14,425

Restar decimales

Al restar fracciones decimales, debes seguir las mismas reglas que al sumar: “coma debajo del punto decimal” e “igual número de dígitos después del punto decimal”.

Ejemplo 1. Encuentra el valor de la expresión 2,5 − 2,2

Escribimos esta expresión en una columna, observando la regla “coma debajo de coma”:

Calculamos la parte fraccionaria 5−2=3. Escribimos el número 3 en la décima parte de nuestra respuesta:

Calculamos la parte entera 2−2=0. Escribimos cero en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Recibimos una respuesta de 0,3. Esto significa que el valor de la expresión 2,5 − 2,2 es igual a 0,3

2,5 − 2,2 = 0,3

Ejemplo 2. Encuentra el valor de la expresión 7.353 - 3.1

Esta expresión tiene un número diferente de dígitos después del punto decimal. La fracción 7.353 tiene tres dígitos después del punto decimal, pero la fracción 3.1 tiene solo uno. Esto significa que en la fracción 3.1 debes agregar dos ceros al final para que el número de dígitos en ambas fracciones sea el mismo. Entonces obtenemos 3.100.

Ahora puedes escribir esta expresión en una columna y calcularla:

Recibimos una respuesta de 4.253. Esto significa que el valor de la expresión 7,353 − 3,1 es igual a 4,253

7,353 — 3,1 = 4,253

Al igual que con los números comunes, a veces tendrás que pedir prestado uno de un dígito adyacente si la resta se vuelve imposible.

Ejemplo 3. Encuentra el valor de la expresión 3,46 − 2,39

Resta centésimas de 6−9. No puedes restar el número 9 del número 6. Por lo tanto, debes pedir prestado uno del dígito adyacente. Al tomar prestado uno del dígito adyacente, el número 6 se convierte en el número 16. Ahora puedes calcular las centésimas de 16−9=7. Escribimos un siete en la centésima parte de nuestra respuesta:

Ahora restamos décimas. Como tomamos una unidad en el lugar de las décimas, la cifra que allí se ubicaba disminuyó en una unidad. En otras palabras, en el lugar de las décimas ahora no está el número 4, sino el número 3. Calculemos las décimas de 3−3=0. Escribimos cero en la décima parte de nuestra respuesta:

Ahora restamos las partes enteras 3−2=1. Escribimos uno en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Recibimos una respuesta de 1,07. Esto significa que el valor de la expresión 3,46−2,39 es igual a 1,07

3,46−2,39=1,07

Ejemplo 4. Encuentra el valor de la expresión 3−1.2

Este ejemplo resta un decimal de un número entero. Escribamos esta expresión en una columna de modo que Toda una parte la fracción decimal 1,23 resultó ser el número 3

Ahora hagamos que el número de dígitos después del punto decimal sea el mismo. Para ello, después del número 3 ponemos una coma y le sumamos un cero:

Ahora restamos décimos: 0−2. No puedes restar el número 2 de cero. Por lo tanto, debes tomar prestado uno del dígito adyacente. Habiendo tomado prestado uno del dígito vecino, 0 se convierte en el número 10. Ahora puedes calcular las décimas de 10−2=8. Escribimos un ocho en la décima parte de nuestra respuesta:

Ahora restamos las partes enteras. Anteriormente, el número 3 estaba en el conjunto, pero le quitamos una unidad. Como resultado, se convirtió en el número 2. Por lo tanto, de 2 restamos 1. 2−1=1. Escribimos uno en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

La respuesta que recibimos fue 1,8. Esto significa que el valor de la expresión 3−1,2 es 1,8

Multiplicar decimales

Multiplicar decimales es sencillo e incluso divertido. Para multiplicar decimales, los multiplicas como números normales, ignorando las comas.

Una vez recibida la respuesta, debe separar la parte entera de la fraccionaria con una coma. Para hacer esto, debe contar la cantidad de dígitos después del punto decimal en ambas fracciones, luego contar la misma cantidad de dígitos desde la derecha en la respuesta y poner una coma.

Ejemplo 1. Encuentra el valor de la expresión 2,5 × 1,5.

Multipliquemos estas fracciones decimales como números ordinarios, ignorando las comas. Para ignorar las comas, puedes imaginar temporalmente que están ausentes por completo:

Obtuvimos 375. En este número, debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debes contar el número de dígitos después del punto decimal en las fracciones 2,5 y 1,5. La primera fracción tiene un dígito después del punto decimal, la segunda fracción también tiene uno. Total dos números.

Volvemos al número 375 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos a la derecha y poner una coma:

Recibimos una respuesta de 3,75. Entonces el valor de la expresión 2,5 × 1,5 es 3,75

2,5 × 1,5 = 3,75

Ejemplo 2. Encuentra el valor de la expresión 12,85 × 2,7

Multipliquemos estas fracciones decimales, ignorando las comas:

Recibimos 34695. En este número, debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debes contar el número de dígitos después del punto decimal en las fracciones 12,85 y 2,7. La fracción 12,85 tiene dos dígitos después del punto decimal y la fracción 2,7 tiene un dígito, un total de tres dígitos.

Volvemos al número 34695 y comenzamos a movernos de derecha a izquierda. Necesitamos contar tres dígitos a la derecha y poner una coma:

Recibimos una respuesta de 34.695. Entonces el valor de la expresión 12,85 × 2,7 es 34,695

12,85 × 2,7 = 34,695

Multiplicar un decimal por un número regular

A veces surgen situaciones en las que necesitas multiplicar una fracción decimal por un número regular.

Para multiplicar un decimal y un número, los multiplicas sin prestar atención a la coma en el decimal. Una vez recibida la respuesta, debe separar la parte entera de la fraccionaria con una coma. Para hacer esto, debe contar la cantidad de dígitos después del punto decimal en la fracción decimal, luego contar la misma cantidad de dígitos desde la derecha en la respuesta y poner una coma.

Por ejemplo, multiplica 2,54 por 2.

Multiplica la fracción decimal 2,54 por el número habitual 2, ignorando la coma:

Obtuvimos el número 508. En este número debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debes contar el número de dígitos después del punto decimal en la fracción 2,54. La fracción 2,54 tiene dos dígitos después del punto decimal.

Volvemos al número 508 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos a la derecha y poner una coma:

Recibimos una respuesta de 5,08. Entonces el valor de la expresión 2,54 × 2 es 5,08

2,54 × 2 = 5,08

Multiplicar decimales por 10, 100, 1000

Multiplicar decimales por 10, 100 o 1000 se realiza de la misma forma que multiplicar decimales por números normales. Debes realizar la multiplicación, sin prestar atención a la coma en la fracción decimal, luego en la respuesta separar la parte entera de la fraccionaria, contando desde la derecha tantos dígitos como dígitos había después del punto decimal.

Por ejemplo, multiplica 2,88 por 10.

Multiplica la fracción decimal 2,88 por 10, ignorando la coma en la fracción decimal:

Obtuvimos 2880. En este número debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debes contar el número de dígitos después del punto decimal en la fracción 2,88. Vemos que la fracción 2,88 tiene dos dígitos después del punto decimal.

Volvemos al número 2880 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos a la derecha y poner una coma:

Recibimos una respuesta de 28,80. Eliminemos el último cero y obtengamos 28,8. Esto significa que el valor de la expresión 2,88×10 es 28,8

2,88 × 10 = 28,8

Existe una segunda forma de multiplicar fracciones decimales por 10, 100, 1000. Este método es mucho más simple y conveniente. Consiste en mover la coma decimal hacia la derecha tantas cifras como ceros tenga el factor.

Por ejemplo, resolvamos el ejemplo anterior 2,88×10 de esta manera. Sin dar ningún cálculo, miramos inmediatamente el factor 10. Nos interesa saber cuántos ceros hay en él. Vemos que hay un cero en él. Ahora en la fracción 2,88 movemos el punto decimal un dígito hacia la derecha, obtenemos 28,8.

2,88 × 10 = 28,8

Intentemos multiplicar 2,88 por 100. Inmediatamente miramos el factor 100. Nos interesa saber cuántos ceros hay en él. Vemos que contiene dos ceros. Ahora en la fracción 2.88 movemos el punto decimal dos dígitos a la derecha, obtenemos 288

2,88 × 100 = 288

Intentemos multiplicar 2,88 por 1000. Inmediatamente miramos el factor 1000. Nos interesa saber cuántos ceros hay en él. Vemos que contiene tres ceros. Ahora en la fracción 2,88 movemos la coma decimal tres dígitos hacia la derecha. No hay un tercer dígito allí, así que agregamos otro cero. Como resultado, obtenemos 2880.

2,88 × 1000 = 2880

Multiplicar decimales por 0,1 0,01 y 0,001

Multiplicar decimales por 0,1, 0,01 y 0,001 funciona de la misma manera que multiplicar un decimal por un decimal. Es necesario multiplicar las fracciones como números ordinarios, y poner una coma en la respuesta, contando tantos dígitos a la derecha como dígitos hay después del punto decimal en ambas fracciones.

Por ejemplo, multiplica 3,25 por 0,1.

Multiplicamos estas fracciones como números ordinarios, ignorando las comas:

Obtuvimos 325. En este número debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debes contar el número de dígitos después del punto decimal en las fracciones 3,25 y 0,1. La fracción 3.25 tiene dos dígitos después del punto decimal y la fracción 0.1 tiene un dígito. Total de tres números.

Volvemos al número 325 y comenzamos a movernos de derecha a izquierda. Necesitamos contar tres dígitos desde la derecha y poner una coma. Después de contar tres dígitos, encontramos que los números se han acabado. En este caso, debe agregar un cero y una coma:

Recibimos una respuesta de 0,325. Esto significa que el valor de la expresión 3,25 × 0,1 es 0,325

3,25 × 0,1 = 0,325

Existe una segunda forma de multiplicar decimales por 0,1, 0,01 y 0,001. Este método es mucho más sencillo y conveniente. Consiste en mover la coma decimal hacia la izquierda tantas cifras como ceros tenga el factor.

Por ejemplo, resolvamos el ejemplo anterior 3,25 × 0,1 de esta manera. Sin hacer ningún cálculo, miramos inmediatamente el multiplicador de 0,1. Nos interesa saber cuántos ceros hay en él. Vemos que hay un cero en él. Ahora en la fracción 3.25 movemos la coma decimal un dígito hacia la izquierda. Moviendo la coma un dígito hacia la izquierda, vemos que no hay más dígitos antes del tres. En este caso, suma un cero y pon una coma. El resultado es 0,325.

3,25 × 0,1 = 0,325

Intentemos multiplicar 3,25 por 0,01. Inmediatamente miramos el multiplicador de 0,01. Nos interesa saber cuántos ceros hay en él. Vemos que contiene dos ceros. Ahora en la fracción 3.25 movemos la coma decimal dos dígitos hacia la izquierda, obtenemos 0.0325

3,25 × 0,01 = 0,0325

Intentemos multiplicar 3,25 por 0,001. Inmediatamente miramos el multiplicador de 0,001. Nos interesa saber cuántos ceros hay en él. Vemos que contiene tres ceros. Ahora en la fracción 3.25 movemos el punto decimal tres dígitos hacia la izquierda, obtenemos 0.00325

3,25 × 0,001 = 0,00325

No confundas multiplicar fracciones decimales por 0,1, 0,001 y 0,001 con multiplicar por 10, 100, 1000. Error común la mayoría de la gente.

Al multiplicar por 10, 100, 1000, el punto decimal se mueve hacia la derecha tantos dígitos como ceros hay en el multiplicador.

Y al multiplicar por 0,1, 0,01 y 0,001, la coma decimal se mueve hacia la izquierda tantos dígitos como ceros haya en el multiplicador.

Si al principio le resulta difícil recordarlo, puede utilizar el primer método, en el que la multiplicación se realiza como con números normales. En la respuesta, deberás separar la parte entera de la parte fraccionaria contando la misma cantidad de dígitos a la derecha que dígitos después del punto decimal en ambas fracciones.

Dividir un número menor por un número mayor. Nivel avanzado.

En una de las lecciones anteriores dijimos que al dividir un número menor por un número mayor se obtiene una fracción cuyo numerador es el dividendo y el denominador es el divisor.

Por ejemplo, para dividir una manzana entre dos, debes escribir 1 (una manzana) en el numerador y 2 (dos amigos) en el denominador. Como resultado, obtenemos la fracción. Esto significa que cada amigo recibirá una manzana. Es decir, media manzana. La fracción es la respuesta al problema. “cómo dividir una manzana en dos”

Resulta que puedes resolver este problema aún más si divides 1 entre 2. Después de todo, la línea fraccionaria en cualquier fracción significa división y, por lo tanto, esta división está permitida en la fracción. ¿Pero cómo? Estamos acostumbrados a que el dividendo siempre sea mayor que el divisor. Pero aquí, por el contrario, el dividendo es menor que el divisor.

Todo quedará claro si recordamos que fracción significa aplastamiento, división, división. Esto significa que la unidad se puede dividir en tantas partes como se desee, y no sólo en dos partes.

Cuando divides un número menor por un número mayor, obtienes una fracción decimal en la que la parte entera es 0 (cero). La parte fraccionaria puede ser cualquier cosa.

Entonces, dividamos 1 entre 2. Resolvamos este ejemplo con una esquina:

Uno no puede dividirse completamente en dos. Si haces una pregunta “cuantos dos hay en uno” , entonces la respuesta será 0. Por tanto, en el cociente escribimos 0 y ponemos una coma:

Ahora, como siempre, multiplicamos el cociente por el divisor para obtener el resto:

Ha llegado el momento en que la unidad se puede dividir en dos partes. Para ello, añade otro cero a la derecha del resultante:

Obtuvimos 10. Dividimos 10 entre 2, obtenemos 5. Escribimos el cinco en la parte fraccionaria de nuestra respuesta:

Ahora sacamos el último resto para completar el cálculo. Multiplica 5 por 2 para obtener 10

Recibimos una respuesta de 0,5. entonces la fraccion es 0.5

También se puede escribir media manzana usando la fracción decimal 0,5. Si sumamos estas dos mitades (0,5 y 0,5), obtenemos nuevamente la manzana entera original:

Este punto también se puede entender si imaginas cómo se divide 1 cm en dos partes. Si divides 1 centímetro en 2 partes, obtienes 0,5 cm.

Ejemplo 2. Encuentra el valor de la expresión 4:5.

¿Cuántos cinco hay en un cuatro? De nada. Escribimos 0 en el cociente y ponemos una coma:

Multiplicamos 0 por 5, obtenemos 0. Escribimos un cero debajo del cuatro. Resta inmediatamente este cero del dividendo:

Ahora comencemos a dividir (dividir) los cuatro en 5 partes. Para hacer esto, sumamos un cero a la derecha de 4 y dividimos 40 entre 5, obtenemos 8. Escribimos ocho en el cociente.

Completamos el ejemplo multiplicando 8 por 5 para obtener 40:

Recibimos una respuesta de 0,8. Esto significa que el valor de la expresión 4:5 es 0,8.

Ejemplo 3. Encuentra el valor de la expresión 5: 125

¿Cuántos números son 125 en cinco? De nada. Escribimos 0 en el cociente y ponemos una coma:

Multiplicamos 0 por 5, obtenemos 0. Escribimos 0 debajo del cinco. Inmediatamente resta 0 de cinco

Ahora comencemos a dividir (dividir) los cinco en 125 partes. Para ello, escribimos un cero a la derecha de este cinco:

Divide 50 entre 125. ¿Cuántos números hay 125 en el número 50? De nada. Entonces en el cociente escribimos 0 nuevamente.

Multiplica 0 por 125, obtenemos 0. Escribe este cero debajo de 50. Inmediatamente resta 0 de 50

Ahora divide el número 50 en 125 partes. Para ello, escribimos otro cero a la derecha de 50:

Divide 500 entre 125. ¿Cuántos números hay 125 en el número 500? Hay cuatro números 125 en el número 500. Escribe el cuatro en el cociente:

Completamos el ejemplo multiplicando 4 por 125 para obtener 500

Recibimos una respuesta de 0,04. Esto significa que el valor de la expresión 5: 125 es 0,04

Dividir números sin resto

Entonces, pongamos una coma en el cociente después de la unidad, indicando así que la división de partes enteras ha terminado y pasamos a la parte fraccionaria:

Sumemos cero al resto 4

Ahora dividimos 40 entre 5, obtenemos 8. Escribimos ocho en el cociente:

40−40=0. Nos queda 0. Esto significa que la división está completamente completa. Al dividir 9 entre 5 se obtiene la fracción decimal 1,8:

9: 5 = 1,8

Ejemplo 2. Dividir 84 entre 5 sin resto

Primero, divide 84 entre 5 como de costumbre con un resto:

Nos quedan 16 en privado y quedan 4 más. Ahora dividamos este resto entre 5. Ponga una coma en el cociente y sume 0 al resto 4.

Ahora dividimos 40 entre 5, obtenemos 8. Escribimos el ocho en el cociente después del punto decimal:

y completa el ejemplo comprobando si aún queda resto:

Dividir un decimal por un número regular

Una fracción decimal, como sabemos, consta de un número entero y una parte fraccionaria. Al dividir una fracción decimal por un número normal, primero debes:

• divide toda la parte de la fracción decimal por este número;
• Después de dividir toda la parte, debes poner inmediatamente una coma en el cociente y continuar con el cálculo, como en la división normal.

Por ejemplo, divide 4,8 entre 2

Escribamos este ejemplo en una esquina:

Ahora dividamos toda la parte entre 2. Cuatro dividido entre dos es igual a dos. Escribimos dos en el cociente e inmediatamente ponemos una coma:

Ahora multiplicamos el cociente por el divisor y vemos si queda resto de la división:

4-4=0. El resto es cero. Todavía no anotamos cero, ya que la solución no está completa. A continuación, continuamos calculando como en la división ordinaria. Saca 8 y divídelo entre 2.

8: 2 = 4. Escribimos el cuatro en el cociente e inmediatamente lo multiplicamos por el divisor:

Recibimos una respuesta de 2,4. El valor de la expresión 4.8:2 es 2.4

Ejemplo 2. Encuentra el valor de la expresión 8.43: 3.

Dividimos 8 entre 3 y obtenemos 2. Inmediatamente ponemos una coma después del 2:

Ahora multiplicamos el cociente por el divisor 2 × 3 = 6. Escribimos el seis debajo del ocho y encontramos el resto:

Dividimos 24 entre 3 y obtenemos 8. Escribimos ocho en el cociente. Multiplícalo inmediatamente por el divisor para encontrar el resto de la división:

24−24=0. El resto es cero. Todavía no escribimos cero. Le quitamos los tres últimos al dividendo y lo dividimos entre 3, obtenemos 1. Inmediatamente multiplicamos 1 por 3 para completar este ejemplo:

La respuesta que recibimos fue 2,81. Esto significa que el valor de la expresión 8,43: 3 es 2,81

Dividir un decimal por un decimal

Para dividir una fracción decimal por una fracción decimal, debe mover el punto decimal en el dividendo y el divisor hacia la derecha la misma cantidad de dígitos que hay después del punto decimal en el divisor, y luego dividir por el número habitual.

Por ejemplo, divida 5,95 entre 1,7

Escribamos esta expresión con una esquina.

Ahora en el dividendo y en el divisor movemos la coma decimal hacia la derecha la misma cantidad de dígitos que hay después de la coma decimal en el divisor. El divisor tiene un dígito después del punto decimal. Esto significa que en el dividendo y divisor debemos mover la coma decimal un dígito hacia la derecha. Transferimos:

Después de mover el punto decimal un dígito hacia la derecha, la fracción decimal 5,95 se convirtió en la fracción 59,5. Y la fracción decimal 1,7, después de mover el punto decimal un dígito hacia la derecha, se convirtió en el número habitual 17. Y ya sabemos cómo dividir una fracción decimal por un número normal. No es difícil realizar más cálculos:

La coma se mueve hacia la derecha para facilitar la división. Esto está permitido porque al multiplicar o dividir el dividendo y el divisor por el mismo número, el cociente no cambia. ¿Qué significa?

Este es uno de características interesantes división. Se llama propiedad del cociente. Considere la expresión 9: 3 = 3. Si en esta expresión el dividendo y el divisor se multiplican o dividen por el mismo número, entonces el cociente 3 no cambiará.

Multipliquemos el dividendo y el divisor por 2 y veamos qué sale de ello:

(9 × 2): (3 × 2) = 18: 6 = 3

Como puede verse en el ejemplo, el cociente no ha cambiado.

Lo mismo ocurre cuando movemos la coma en el dividendo y en el divisor. En el ejemplo anterior, donde dividimos 5,91 entre 1,7, movimos la coma en el dividendo y el divisor un dígito hacia la derecha. Después de mover el punto decimal, la fracción 5,91 se transformó en la fracción 59,1 y la fracción 1,7 se transformó en el habitual número 17.

De hecho, dentro de este proceso había una multiplicación por 10. Así se veía:

5,91 × 10 = 59,1

Por lo tanto, el número de dígitos después del punto decimal en el divisor determina por qué se multiplicarán el dividendo y el divisor. En otras palabras, el número de dígitos después del punto decimal en el divisor determinará cuántos dígitos en el dividendo y en el divisor el punto decimal se moverá hacia la derecha.

Dividir un decimal por 10, 100, 1000

Dividir un decimal entre 10, 100 o 1000 se hace de la misma manera que. Por ejemplo, divide 2,1 entre 10. Resuelve este ejemplo usando una esquina:

Pero hay una segunda manera. Es más ligero. La esencia de este método es que la coma en el dividendo se mueve hacia la izquierda tantos dígitos como ceros hay en el divisor.

Resolvamos el ejemplo anterior de esta manera. 2.1: 10. Nos fijamos en el divisor. Nos interesa saber cuántos ceros hay en él. Vemos que hay un cero. Esto significa que en el dividendo de 2,1 debes mover la coma decimal un dígito hacia la izquierda. Movemos la coma un dígito hacia la izquierda y vemos que no quedan más dígitos. En este caso, agregue otro cero antes del número. Como resultado obtenemos 0,21

Intentemos dividir 2,1 entre 100. Hay dos ceros en 100. Esto significa que en el dividendo 2.1 necesitamos mover la coma dos dígitos hacia la izquierda:

2,1: 100 = 0,021

Intentemos dividir 2,1 entre 1000. Hay tres ceros en 1000. Esto significa que en el dividendo 2.1 debes mover la coma tres dígitos hacia la izquierda:

2,1: 1000 = 0,0021

Dividir un decimal entre 0,1, 0,01 y 0,001

Dividir una fracción decimal entre 0,1, 0,01 y 0,001 se realiza de la misma forma que. En el dividendo y en el divisor, debes mover el punto decimal hacia la derecha tantos dígitos como haya después del punto decimal en el divisor.

Por ejemplo, dividamos 6,3 entre 0,1. En primer lugar, muevamos las comas del dividendo y el divisor hacia la derecha la misma cantidad de dígitos que hay después del punto decimal en el divisor. El divisor tiene un dígito después del punto decimal. Esto significa que movemos las comas en el dividendo y el divisor un dígito hacia la derecha.

Después de mover el punto decimal un dígito hacia la derecha, la fracción decimal 6,3 se convierte en el número habitual 63, y la fracción decimal 0,1 después de mover el punto decimal un dígito hacia la derecha se convierte en uno. Y dividir 63 entre 1 es muy sencillo:

Esto significa que el valor de la expresión 6.3: 0.1 es 63.

Pero hay una segunda manera. Es más ligero. La esencia de este método es que la coma en el dividendo se mueve hacia la derecha tantos dígitos como ceros hay en el divisor.

Resolvamos el ejemplo anterior de esta manera. 6,3: 0,1. Miremos el divisor. Nos interesa saber cuántos ceros hay en él. Vemos que hay un cero. Esto significa que en el dividendo de 6,3 debes mover el punto decimal un dígito hacia la derecha. Mueva la coma un dígito hacia la derecha y obtenga 63

Intentemos dividir 6,3 entre 0,01. El divisor de 0,01 tiene dos ceros. Esto significa que en el dividendo 6.3 necesitamos mover la coma decimal dos dígitos hacia la derecha. Pero en el dividendo sólo hay un dígito después del punto decimal. En este caso, deberás agregar otro cero al final. Como resultado obtenemos 630

Intentemos dividir 6,3 entre 0,001. El divisor de 0,001 tiene tres ceros. Esto significa que en el dividendo 6.3 necesitamos mover la coma decimal tres dígitos hacia la derecha:

6,3: 0,001 = 6300

Tareas para una solución independiente.

¿Te gustó la lección?
Únete a nuestro nuevo grupo VKontakte y comienza a recibir notificaciones sobre nuevas lecciones

Dedicaremos este material a un tema tan importante como las fracciones decimales. Primero, definamos las definiciones básicas, demos ejemplos y detengámonos en las reglas de la notación decimal, así como en cuáles son los dígitos de las fracciones decimales. A continuación, destacamos los principales tipos: fracciones finitas e infinitas, periódicas y no periódicas. En la parte final mostraremos cómo se ubican los puntos correspondientes a números fraccionarios en el eje de coordenadas.

Yandex.RTB R-A-339285-1

¿Qué es la notación decimal de números fraccionarios?

La llamada notación decimal de números fraccionarios se puede utilizar tanto para números naturales como para números fraccionarios. Parece un conjunto de dos o más números con una coma entre ellos.

El punto decimal es necesario para separar la parte entera de la parte fraccionaria. Como regla general, el último dígito de una fracción decimal no es un cero, a menos que el punto decimal aparezca inmediatamente después del primer cero.

¿Cuáles son algunos ejemplos de números fraccionarios en notación decimal? Esto podría ser 34, 21, 0, 35035044, 0, 0001, 11,231,552, 9, etc.

En algunos libros de texto se puede encontrar el uso de un punto en lugar de una coma (5. 67, 6789. 1011, etc.). Esta opción se considera equivalente, pero es más típica de las fuentes en inglés.

Definición de decimales

Basándonos en el concepto anterior de notación decimal, podemos formular la siguiente definición de fracciones decimales:

Definición 1

Los decimales representan números fraccionarios en notación decimal.

¿Por qué necesitamos escribir fracciones en esta forma? Nos aporta algunas ventajas respecto a los ordinarios, por ejemplo, una notación más compacta, sobre todo en los casos en que el denominador contiene 1000, 100, 10, etc., o un número mixto. Por ejemplo, en lugar de 6 10 podemos especificar 0,6, en lugar de 25 10000 - 0,0023, en lugar de 512 3 100 - 512,03.

En un material aparte se analizará cómo representar correctamente fracciones ordinarias con decenas, centenas y miles en el denominador en forma decimal.

Cómo leer decimales correctamente

Existen algunas reglas para leer notaciones decimales. Así, aquellas fracciones decimales que corresponden a sus equivalentes ordinarios se leen casi de la misma manera, pero con la adición de las palabras “cero décimas” al principio. Así, la entrada 0, 14, que corresponde a 14.100, se lee “cero coma catorce centésimas”.

Si una fracción decimal se puede asociar con un número mixto, entonces se lee de la misma manera que este número. Entonces, si tenemos la fracción 56, 002, que corresponde a 56 2 1000, leemos esta entrada como “cincuenta y seis coma dos milésimas”.

El significado de un dígito en una fracción decimal depende de dónde se encuentre (lo mismo que en el caso de los números naturales). Entonces, en la fracción decimal 0,7, siete son décimas, en 0,0007 son diezmilésimas y en la fracción 70.000,345 significa siete decenas de miles de unidades enteras. Así, en las fracciones decimales también existe el concepto de valor posicional.

Los nombres de los dígitos ubicados antes del punto decimal son similares a los que existen en los números naturales. Los nombres de los que se encuentran después se presentan claramente en la tabla:

Veamos un ejemplo.

Ejemplo 1

Tenemos la fracción decimal 43.098. Tiene un cuatro en el lugar de las decenas, un tres en el lugar de las unidades, un cero en el lugar de las décimas, un 9 en el lugar de las centésimas y un 8 en el lugar de las milésimas.

Se acostumbra distinguir los rangos de fracciones decimales por precedencia. Si recorremos los números de izquierda a derecha, entonces pasaremos del más significativo al menos significativo. Resulta que las centenas son mayores que las decenas y las partes por millón son menores que las centésimas. Si tomamos la fracción decimal final que citamos como ejemplo anteriormente, entonces el lugar más alto o más alto será el lugar de las centenas, y el lugar más bajo o más bajo será el lugar de las 10 milésimas.

Cualquier fracción decimal se puede expandir a dígitos individuales, es decir, presentarse como una suma. Esta acción se realiza de la misma manera que para números naturales.

Ejemplo 2

Intentemos expandir la fracción 56, 0455 a dígitos.

Obtendremos:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Si recordamos las propiedades de la suma, podemos representar esta fracción en otras formas, por ejemplo, como la suma 56 + 0, 0455, o 56, 0055 + 0, 4, etc.

¿Qué son los decimales finales?

Todas las fracciones de las que hablamos anteriormente son finitas. decimales. Esto significa que el número de dígitos después del punto decimal es finito. Derivemos la definición:

Definición 1

Los decimales finales son un tipo de fracción decimal que tiene un número finito de decimales después del signo decimal.

Ejemplos de tales fracciones pueden ser 0, 367, 3, 7, 55, 102567958, 231 032, 49, etc.

Cualquiera de estas fracciones se puede convertir a un número mixto (si el valor de su parte fraccionaria es diferente de cero) o a fracción común(con parte entera cero). Hemos dedicado un artículo aparte a cómo se hace esto. Aquí sólo señalaremos un par de ejemplos: por ejemplo, podemos reducir la fracción decimal final 5, 63 a la forma 5 63 100, y 0, 2 corresponde a 2 10 (o cualquier otra fracción igual a ella, por ejemplo). ejemplo, 4 20 o 1 5.)

Pero el proceso inverso, es decir. Es posible que no siempre sea posible escribir una fracción común en forma decimal. Entonces, 5 13 no se puede reemplazar por una fracción igual con denominador 100, 10, etc., lo que significa que a partir de ella no se puede obtener una fracción decimal final.

Principales tipos de fracciones decimales infinitas: fracciones periódicas y no periódicas

Indicamos anteriormente que las fracciones finitas se llaman así porque tienen un número finito de dígitos después del punto decimal. Sin embargo, bien puede ser infinito, en cuyo caso las fracciones mismas también se llamarán infinitas.

Definición 2

Las fracciones decimales infinitas son aquellas que tienen un número infinito de dígitos después del punto decimal.

Obviamente, tales números simplemente no se pueden escribir en su totalidad, por lo que indicamos solo una parte de ellos y luego agregamos puntos suspensivos. Este signo indica una continuación infinita de la secuencia de decimales. Ejemplos de fracciones decimales infinitas incluyen 0, 143346732…, ​​3, 1415989032…, 153, 0245005…, 2, 66666666666…, 69, 748768152…. etc.

La “cola” de tal fracción puede contener no sólo secuencias de números aparentemente aleatorias, sino también repetición constante el mismo signo o grupo de signos. Las fracciones con números alternos después del punto decimal se llaman periódicas.

Definición 3

Las fracciones decimales periódicas son aquellas fracciones decimales infinitas en las que se repite un dígito o un grupo de varios dígitos después de la coma decimal. La parte que se repite se llama período de la fracción.

Por ejemplo, para la fracción 3, 444444…. el período será el número 4, y para 76, 134134134134... - el grupo 134.

¿Cuál es el número mínimo de caracteres que se pueden dejar en la notación de una fracción periódica? Para fracciones periódicas, bastará con escribir el período completo una vez entre paréntesis. Entonces, fracción 3, 444444…. Sería correcto escribirlo como 3, (4), y 76, 134134134134... – como 76, (134).

En general, las entradas con varios puntos entre paréntesis tendrán exactamente el mismo significado: por ejemplo, la fracción periódica 0,677777 es lo mismo que 0,6 (7) y 0,6 (77), etc. También son aceptables registros del formulario 0, 67777 (7), 0, 67 (7777), etc.

Para evitar errores, introducimos uniformidad de notación. Acordemos escribir solo un punto (la secuencia de números más corta posible), que esté más cerca del punto decimal, y encerrarlo entre paréntesis.

Es decir, para la fracción anterior consideraremos que la entrada principal es 0, 6 (7) y, por ejemplo, en el caso de la fracción 8, 9134343434 escribiremos 8, 91 (34).

Si el denominador de una fracción ordinaria contiene factores primos que no son iguales a 5 y 2, cuando se conviertan a notación decimal, darán como resultado fracciones infinitas.

En principio, podemos escribir cualquier fracción finita como periódica. Para hacer esto, solo necesitamos agregar un número infinito de ceros a la derecha. ¿Cómo se ve en la grabación? Digamos que tenemos la fracción final 45, 32. En forma periódica se verá como 45, 32 (0). Esta acción es posible porque sumar ceros a la derecha de cualquier fracción decimal nos da el resultado de una fracción igual a ella.

Se debe prestar especial atención a las fracciones periódicas con un período de 9, por ejemplo, 4, 89 (9), 31, 6 (9). Son una notación alternativa para fracciones similares con un período de 0, por lo que a menudo se reemplazan al escribir con fracciones con un período de cero. En este caso, se suma uno al valor del siguiente dígito y (0) se indica entre paréntesis. La igualdad de los números resultantes se puede verificar fácilmente representándolos como fracciones ordinarias.

Por ejemplo, la fracción 8, 31 (9) se puede sustituir por la correspondiente fracción 8, 32 (0). O 4, (9) = 5, (0) = 5.

Las fracciones periódicas decimales infinitas se refieren a numeros racionales. En otras palabras, cualquier fracción periódica se puede representar como una fracción ordinaria y viceversa.

También hay fracciones que no tienen una secuencia que se repite infinitamente después del punto decimal. En este caso se denominan fracciones no periódicas.

Definición 4

Las fracciones decimales no periódicas incluyen aquellas fracciones decimales infinitas que no contienen un punto después del punto decimal, es decir grupo repetido de números.

A veces, las fracciones no periódicas se parecen mucho a las periódicas. Por ejemplo 9, 03003000300003... a primera vista parece tener un punto, sin embargo análisis detallado Los decimales confirman que todavía se trata de una fracción no periódica. Hay que tener mucho cuidado con esos números.

Las fracciones no periódicas se clasifican como números irracionales. No se convierten a fracciones ordinarias.

Operaciones básicas con decimales.

Se pueden realizar las siguientes operaciones con fracciones decimales: comparación, resta, suma, división y multiplicación. Veamos cada uno de ellos por separado.

Comparar decimales se puede reducir a comparar fracciones que corresponden a los decimales originales. Pero las infinitas fracciones no periódicas no se pueden reducir a esta forma, y ​​convertir fracciones decimales en fracciones ordinarias suele ser una tarea que requiere mucha mano de obra. ¿Cómo podemos realizar rápidamente una acción de comparación si necesitamos hacer esto mientras resolvemos un problema? Es conveniente comparar fracciones decimales por dígito de la misma manera que comparamos números naturales. Dedicaremos un artículo aparte a este método.

Para sumar unas fracciones decimales con otras es conveniente utilizar el método de suma en columnas, como para los números naturales. Para sumar fracciones decimales periódicas, primero debe reemplazarlas por fracciones ordinarias y contar de acuerdo con el esquema estándar. Si, de acuerdo con las condiciones del problema, necesitamos sumar infinitas fracciones no periódicas, primero debemos redondearlas a un dígito determinado y luego sumarlas. Cuanto menor sea el dígito al que redondeemos, mayor será la precisión del cálculo. Para la resta, multiplicación y división de fracciones infinitas, también es necesario el redondeo previo.

Encontrar la diferencia entre fracciones decimales es lo inverso de la suma. Básicamente, usando la resta podemos encontrar un número cuya suma con la fracción que estamos restando nos dará la fracción que estamos minimizando. Hablaremos de esto con más detalle en un artículo aparte.

La multiplicación de fracciones decimales se realiza de la misma forma que para los números naturales. Para ello también es adecuado el método de cálculo por columnas. Nuevamente reducimos esta acción con fracciones periódicas a la multiplicación de fracciones ordinarias según las reglas ya estudiadas. Las fracciones infinitas, como recordamos, deben redondearse antes de realizar los cálculos.

El proceso de dividir decimales es el inverso de multiplicar. Al resolver problemas, también utilizamos cálculos en columnas.

Puedes establecer una correspondencia exacta entre la fracción decimal final y un punto en el eje de coordenadas. Averigüemos cómo marcar un punto en el eje que corresponda exactamente a la fracción decimal requerida.

Ya hemos estudiado cómo construir puntos correspondientes a fracciones ordinarias, pero las fracciones decimales se pueden reducir a esta forma. Por ejemplo, la fracción común 14 10 es igual a 1, 4, por lo que el punto correspondiente se alejará del origen en dirección positiva exactamente la misma distancia:

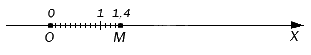
Puede prescindir de reemplazar la fracción decimal por una ordinaria, pero utilice el método de expansión por dígitos como base. Entonces, si necesitamos marcar un punto cuya coordenada será igual a 15, 4008, primero presentaremos este número como la suma 15 + 0, 4 +, 0008. Para empezar, apartemos 15 segmentos unitarios completos en la dirección positiva desde el comienzo de la cuenta regresiva, luego 4 décimas de un segmento y luego 8 diezmilésimas de un segmento. Como resultado, obtenemos un punto de coordenadas que corresponde a la fracción 15, 4008.

Para una fracción decimal infinita, es mejor utilizar este método, ya que te permite acercarte lo más que quieras al punto deseado. En algunos casos, es posible construir una correspondencia exacta con una fracción infinita en el eje de coordenadas: por ejemplo, 2 = 1, 41421. . . , y esta fracción se puede asociar con un punto del rayo de coordenadas, distante de 0 por la longitud de la diagonal del cuadrado, cuyo lado será igual a un segmento unitario.

Si no encontramos un punto en el eje, sino una fracción decimal correspondiente a él, entonces esta acción se llama medición decimal de un segmento. Veamos cómo hacer esto correctamente.

Digamos que necesitamos ir de cero a más allá. este punto en el eje de coordenadas (o acercarse lo más posible en el caso de una fracción infinita). Para ello, vamos posponiendo poco a poco segmentos unitarios desde el origen hasta llegar al punto deseado. Después de segmentos enteros, si es necesario, medimos décimas, centésimas y fracciones más pequeñas para que la coincidencia sea lo más precisa posible. Como resultado, recibimos una fracción decimal que corresponde a Punto dado en el eje de coordenadas.

Arriba mostramos un dibujo con el punto M. Míralo de nuevo: para llegar a este punto es necesario medir un segmento unitario y cuatro décimas del mismo desde cero, ya que este punto corresponde a la fracción decimal 1, 4.

Si no podemos llegar a un punto en el proceso de medición decimal, entonces significa que corresponde a una fracción decimal infinita.

Si nota un error en el texto, resáltelo y presione Ctrl+Enter

Sucede que, para facilitar los cálculos, es necesario convertir una fracción ordinaria a un decimal y viceversa. Hablaremos sobre cómo hacer esto en este artículo. Veamos las reglas para convertir fracciones ordinarias a decimales y viceversa, y también demos ejemplos.

Yandex.RTB R-A-339285-1

Consideraremos convertir fracciones ordinarias a decimales, siguiendo una secuencia determinada. Primero, veamos cómo las fracciones ordinarias con un denominador múltiplo de 10 se convierten a decimales: 10, 100, 1000, etc. Las fracciones con tales denominadores son, de hecho, una notación más engorrosa de fracciones decimales.

A continuación, veremos cómo convertir fracciones ordinarias con cualquier denominador, no sólo múltiplos de 10, en fracciones decimales. Tenga en cuenta que al convertir fracciones ordinarias a decimales, no solo se obtienen decimales finitos, sino también fracciones decimales periódicas infinitas.

¡Empecemos!

Traducción de fracciones ordinarias con denominadores 10, 100, 1000, etc. a decimales

En primer lugar, digamos que algunas fracciones requieren cierta preparación antes de convertirse a forma decimal. ¿Qué es? Antes del número en el numerador, debes agregar tantos ceros para que el número de dígitos en el numerador sea igual al número de ceros en el denominador. Por ejemplo, para la fracción 3100, el número 0 se debe sumar una vez a la izquierda del 3 en el numerador. La fracción 610, según la regla antes expuesta, no necesita modificación.

Consideremos un ejemplo más, después del cual formularemos una regla que es especialmente conveniente de usar al principio, aunque no hay mucha experiencia en la conversión de fracciones. Entonces, la fracción 1610000 después de agregar ceros en el numerador se verá como 001510000.

Cómo convertir una fracción común con denominador 10, 100, 1000, etc. a decimales?

Regla para convertir fracciones propias ordinarias a decimales

1. Escribe 0 y pon una coma después.
2. Anotamos el número del numerador que se obtuvo después de sumar ceros.

Ahora pasemos a los ejemplos.

Ejemplo 1: convertir fracciones a decimales

Convirtamos la fracción 39.100 a decimal.

Primero, miramos la fracción y vemos que no es necesario realizar ninguna acción preparatoria: el número de dígitos en el numerador coincide con el número de ceros en el denominador.

Siguiendo la regla, escribimos 0, ponemos un punto decimal después y escribimos el número del numerador. Obtenemos la fracción decimal 0,39.

Veamos la solución a otro ejemplo sobre este tema.

Ejemplo 2. Convertir fracciones a decimales

Escribamos la fracción 105 10000000 como decimal.

El número de ceros en el denominador es 7 y el numerador tiene solo tres dígitos. Agreguemos 4 ceros más antes del número en el numerador:

0000105 10000000

Ahora escribimos 0, ponemos un punto decimal después y anotamos el número del numerador. Obtenemos la fracción decimal 0,0000105.

Las fracciones consideradas en todos los ejemplos son fracciones propias ordinarias. Pero, ¿cómo se convierte una fracción impropia a decimal? Digamos de inmediato que no es necesario prepararse para sumar ceros a tales fracciones. Formulemos una regla.

Regla para convertir fracciones impropias ordinarias a decimales

1. Escribe el número que está en el numerador.
2. Usamos un punto decimal para separar tantos dígitos a la derecha como ceros hay en el denominador de la fracción original.

A continuación se muestra un ejemplo de cómo utilizar esta regla.

Ejemplo 3. Convertir fracciones a decimales

Convirtamos la fracción 56888038009 100000 de una fracción irregular ordinaria a un decimal.

Primero, escribamos el número del numerador:

Ahora, a la derecha, separamos cinco dígitos con un punto decimal (el número de ceros en el denominador es cinco). Obtenemos:

La siguiente pregunta que surge naturalmente es: cómo convertir un número mixto en una fracción decimal si el denominador de su parte fraccionaria es el número 10, 100, 1000, etc. Para convertir dicho número a una fracción decimal, puede utilizar la siguiente regla.

Regla para convertir números mixtos a decimales

1. Preparamos la parte fraccionaria del número, si es necesario.
2. Anotamos la parte entera del número original y le ponemos una coma después.
3. Anotamos el número del numerador de la parte fraccionaria junto con los ceros añadidos.

Veamos un ejemplo.

Ejemplo 4: convertir números mixtos a decimales

Convirtamos el número mixto 23 17 10000 a una fracción decimal.

En la parte fraccionaria tenemos la expresión 17 10000. Preparémoslo y agreguemos dos ceros más a la izquierda del numerador. Obtenemos: 0017 10000.

Ahora escribimos la parte entera del número y le ponemos una coma después: 23, . .

Después del punto decimal, escribe el número del numerador junto con ceros. Obtenemos el resultado:

23 17 10000 = 23 , 0017

Convertir fracciones ordinarias en fracciones periódicas finitas e infinitas

Por supuesto, puedes convertir a decimales y fracciones ordinarias con un denominador distinto de 10, 100, 1000, etc.

A menudo, una fracción se puede reducir fácilmente a un nuevo denominador y luego utilizar la regla establecida en el primer párrafo de este artículo. Por ejemplo, basta con multiplicar el numerador y el denominador de la fracción 25 por 2 y obtenemos la fracción 410, que se convierte fácilmente a la forma decimal 0,4.

Sin embargo, este método de convertir una fracción a decimal no siempre se puede utilizar. A continuación consideraremos qué hacer si es imposible aplicar el método considerado.

Una forma fundamentalmente nueva de convertir una fracción a decimal es dividir el numerador por el denominador con una columna. Esta operación es muy similar a dividir números naturales con una columna, pero tiene sus propias características.

El numerador al dividir se representa como una fracción decimal, a la derecha de último dígito El numerador va precedido de una coma y se añaden ceros. En el cociente resultante se coloca un punto decimal cuando finaliza la división de la parte entera del numerador. Cómo funciona exactamente este método quedará claro después de observar los ejemplos.

Ejemplo 5. Convertir fracciones a decimales

Convirtamos la fracción común 621 4 a forma decimal.

Representemos el número 621 del numerador como una fracción decimal, agregando algunos ceros después del punto decimal. 621 = 621,00

Ahora dividamos 621,00 entre 4 usando una columna. Los primeros tres pasos de la división serán los mismos que cuando se dividen números naturales, y obtendremos.

Cuando llegamos al punto decimal en el dividendo, y el resto es distinto de cero, ponemos un punto decimal en el cociente y seguimos dividiendo, sin prestar más atención a la coma en el dividendo.

Como resultado, obtenemos la fracción decimal 155, 25, que es el resultado de invertir la fracción común 621 4

621 4 = 155 , 25

Veamos otro ejemplo para reforzar el material.

Ejemplo 6. Convertir fracciones a decimales

Inviertamos la fracción común 21 800.

Para ello, divide la fracción 21.000 en una columna entre 800. La división de la parte entera terminará en el primer paso, por lo que inmediatamente después ponemos un punto decimal en el cociente y continuamos la división, sin prestar atención a la coma en el dividendo hasta que obtengamos un resto igual a cero.

Como resultado, obtuvimos: 21.800 = 0,02625.

Pero, ¿qué pasa si al dividir todavía no obtenemos un resto de 0? En tales casos, la división puede continuar indefinidamente. Sin embargo, a partir de un determinado paso, los residuos se repetirán periódicamente. En consecuencia, se repetirán los números del cociente. Esto significa que una fracción ordinaria se convierte en una fracción periódica infinita decimal. Ilustremos esto con un ejemplo.

Ejemplo 7. Convertir fracciones a decimales

Convirtamos la fracción común 19 44 a decimal. Para ello, realizamos división por columna.

Vemos que durante la división se repiten los residuos 8 y 36. En este caso se repiten los números 1 y 8 en el cociente. Este es el período en fracción decimal. Al grabar, estos números se colocan entre paréntesis.

Por tanto, la fracción ordinaria original se convierte en una fracción decimal periódica infinita.

19 44 = 0 , 43 (18) .

Veamos una fracción ordinaria irreducible. ¿Qué forma adoptará? ¿Qué fracciones ordinarias se convierten a decimales finitos y cuáles a infinitas periódicas?

Primero, digamos que si una fracción se puede reducir a uno de los denominadores 10, 100, 1000..., entonces tendrá la forma de una fracción decimal final. Para que una fracción pueda reducirse a uno de estos denominadores, su denominador debe ser divisor de al menos uno de los números 10, 100, 1000, etc. De las reglas para factorizar números en factores primos se deduce que el divisor de números es 10, 100, 1000, etc. debe, cuando se factoriza en factores primos, contener solo los números 2 y 5.

Resumamos lo dicho:

1. Una fracción común se puede reducir a un decimal final si su denominador se puede factorizar en factores primos de 2 y 5.
2. Si, además de los números 2 y 5, hay otros números primos en el desarrollo del denominador, la fracción se reduce a la forma de una fracción decimal periódica infinita.

Pongamos un ejemplo.

Ejemplo 8. Convertir fracciones a decimales

¿Cuál de estas fracciones 47 20, 7 12, 21 56, 31 17 se convierte en una fracción decimal final y cuál, solo en una periódica? Respondamos esta pregunta sin convertir directamente una fracción a decimal.

La fracción 47 20, como es fácil comprobar, al multiplicar el numerador y el denominador por 5 se reduce a un nuevo denominador 100.

47 20 = 235 100. De esto concluimos que esta fracción se convierte a una fracción decimal final.

Factorizar el denominador de la fracción 7 12 da 12 = 2 2 3. Dado que el factor primo 3 es diferente de 2 y 5, esta fracción no se puede representar como una fracción decimal finita, sino que tendrá la forma de una fracción periódica infinita.

En primer lugar, es necesario reducir la fracción 21 56. Después de reducir por 7, obtenemos la fracción irreducible 3 8, cuyo denominador se factoriza para dar 8 = 2 · 2 · 2. Por tanto, es una fracción decimal final.

En el caso de la fracción 31 17, factorizar el denominador es el propio número primo 17. En consecuencia, esta fracción se puede convertir en una fracción decimal periódica infinita.

Una fracción ordinaria no se puede convertir en una fracción decimal infinita y no periódica.

Arriba hablamos solo de fracciones periódicas finitas e infinitas. Pero, ¿se puede convertir cualquier fracción ordinaria en una fracción infinita no periódica?

Respondemos: ¡no!

¡Importante!

Al convertir una fracción infinita a decimal, el resultado es un decimal finito o un decimal periódico infinito.

El resto de una división siempre es menor que el divisor. En otras palabras, según el teorema de divisibilidad, si dividimos algún número natural por el número q, entonces el resto de la división en cualquier caso no puede ser mayor que q-1. Una vez completada la división, es posible una de las siguientes situaciones:

1. Obtenemos un resto de 0, y aquí es donde termina la división.
2. Obtenemos un resto, que se repite en la división posterior, lo que da como resultado una fracción periódica infinita.

No puede haber otras opciones al convertir una fracción a decimal. Digamos también que la duración del período (número de dígitos) en una fracción periódica infinita es siempre menor que el número de dígitos en el denominador de la fracción ordinaria correspondiente.

Convertir decimales a fracciones

Ahora es el momento de ver el proceso inverso de convertir una fracción decimal en una fracción común. Formulemos una regla de traducción que incluya tres etapas. ¿Cómo convertir una fracción decimal a una fracción común?

Regla para convertir fracciones decimales a fracciones ordinarias

1. En el numerador escribimos el número de la fracción decimal original, descartando la coma y todos los ceros de la izquierda, si los hubiera.
2. En el denominador escribimos uno seguido de tantos ceros como dígitos haya después del punto decimal en la fracción decimal original.
3. Si es necesario, reduzca la fracción ordinaria resultante.

Consideremos la aplicación. de esta regla con ejemplos.

Ejemplo 8. Convertir fracciones decimales en fracciones ordinarias

Imaginemos el número 3,025 como una fracción ordinaria.

1. Escribimos la propia fracción decimal en el numerador, descartando la coma: 3025.
2. En el denominador escribimos uno, y después tres ceros; esta es exactamente la cantidad de dígitos que contiene la fracción original después del punto decimal: 3025 1000.
3. La fracción resultante 3025 1000 se puede reducir en 25, dando como resultado: 3025 1000 = 121 40.

Ejemplo 9. Convertir fracciones decimales a fracciones ordinarias

Convirtamos la fracción 0,0017 de decimal a ordinaria.

1. En el numerador escribimos la fracción 0, 0017, descartando la coma y los ceros de la izquierda. Resultarán 17.
2. Escribimos uno en el denominador, y después escribimos cuatro ceros: 17 10000. Esta fracción es irreducible.

Si una fracción decimal tiene una parte entera, dicha fracción se puede convertir inmediatamente en un número mixto. ¿Cómo hacerlo?

Formulemos una regla más.

Regla para convertir decimales a números mixtos.

1. El número antes del punto decimal en la fracción se escribe como la parte entera del número mixto.
2. En el numerador escribimos el número después de la coma decimal de la fracción, descartando los ceros de la izquierda si los hay.
3. En el denominador de la parte fraccionaria sumamos uno y tantos ceros como dígitos haya después del punto decimal en la parte fraccionaria.

Tomemos un ejemplo

Ejemplo 10: convertir un decimal en un número mixto

Imaginemos la fracción 155, 06005 como un número mixto.

1. Escribimos el número 155 como parte entera.
2. En el numerador escribimos los números después de la coma decimal, descartando el cero.
3. Escribimos uno y cinco ceros en el denominador.

Aprendamos un número mixto: 155 6005 100000

La parte fraccionaria se puede reducir en 5. Lo acortamos y obtenemos el resultado final:

155 , 06005 = 155 1201 20000

Convertir infinitos decimales periódicos a fracciones

Veamos ejemplos de cómo convertir fracciones decimales periódicas en fracciones ordinarias. Antes de comenzar, aclaremos: cualquier fracción decimal periódica se puede convertir en una fracción ordinaria.

El caso más sencillo es cuando el período de la fracción es cero. Una fracción periódica con un período cero se reemplaza por una fracción decimal final, y el proceso de revertir dicha fracción se reduce a revertir la fracción decimal final.

Ejemplo 11. Convertir una fracción decimal periódica a una fracción común

Invirtamos la fracción periódica 3, 75 (0).

Eliminando los ceros de la derecha, obtenemos la fracción decimal final 3,75.

Convirtiendo esta fracción a una fracción ordinaria usando el algoritmo discutido en los párrafos anteriores, obtenemos:

3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .

¿Qué pasa si el período de la fracción es distinto de cero? La parte periódica debe considerarse como la suma de los términos de una progresión geométrica, que decrece. Expliquemos esto con un ejemplo:

0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Existe una fórmula para la suma de términos de una progresión geométrica decreciente infinita. Si el primer término de la progresión es b y el denominador q es tal que 0< q < 1 , то сумма равна b 1 - q .

Veamos algunos ejemplos usando esta fórmula.

Ejemplo 12. Convertir una fracción decimal periódica a una fracción común

Tengamos una fracción periódica 0, (8) y necesitamos convertirla a una fracción ordinaria.

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Aquí tenemos una disminución infinita. progresión geométrica con el primer término 0, 8 y el denominador 0, 1.

Apliquemos la fórmula:

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9

Esta es la fracción ordinaria requerida.

Para consolidar el material, considere otro ejemplo.

Ejemplo 13. Convertir una fracción decimal periódica a una fracción común

Inviertamos la fracción 0, 43 (18).

Primero escribimos la fracción como una suma infinita:

0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)

Veamos los términos entre paréntesis. Esta progresión geométrica se puede representar de la siguiente manera:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Sumamos el resultado a la fracción final 0, 43 = 43 100 y obtenemos el resultado:

0 , 43 (18) = 43 100 + 18 9900

Después de sumar estas fracciones y reducir, obtenemos la respuesta final:

0 , 43 (18) = 19 44

Para concluir este artículo, diremos que las fracciones decimales infinitas no periódicas no se pueden convertir en fracciones ordinarias.

Si nota un error en el texto, resáltelo y presione Ctrl+Enter

Este artículo trata sobre decimales. Aquí entenderemos la notación decimal de números fraccionarios, introduciremos el concepto de fracción decimal y daremos ejemplos de fracciones decimales. A continuación hablaremos de los dígitos de las fracciones decimales y daremos los nombres de los dígitos. Después de esto, nos centraremos en fracciones decimales infinitas, hablemos de fracciones periódicas y no periódicas. A continuación enumeramos las operaciones básicas con fracciones decimales. En conclusión, establezcamos la posición de las fracciones decimales en el haz de coordenadas.

Navegación de páginas.

Notación decimal de un número fraccionario

Lectura de decimales

Digamos algunas palabras sobre las reglas para leer fracciones decimales.

Las fracciones decimales, que corresponden a fracciones ordinarias propias, se leen de la misma manera que estas fracciones ordinarias, sólo que primero se suma "entero cero". Por ejemplo, la fracción decimal 0,12 corresponde a la fracción común 12/100 (léase “doce centésimas”), por lo tanto, 0,12 se lee como “cero coma doce centésimas”.

Las fracciones decimales que corresponden a números mixtos se leen exactamente igual que estos números mixtos. Por ejemplo, la fracción decimal 56.002 corresponde a un número mixto, por lo que la fracción decimal 56.002 se lee como “cincuenta y seis coma dos milésimas”.

Lugares en decimales

Al escribir fracciones decimales, así como al escribir números naturales, el significado de cada dígito depende de su posición. De hecho, el número 3 en la fracción decimal 0,3 significa tres décimas, en la fracción decimal 0,0003, tres diezmilésimas y en la fracción decimal 30.000,152, tres decenas de miles. Entonces podemos hablar de lugares decimales, así como sobre los dígitos de los números naturales.

Los nombres de los dígitos de la fracción decimal hasta la coma decimal coinciden completamente con los nombres de los dígitos de los números naturales. Y los nombres de los lugares decimales después del punto decimal se pueden ver en la siguiente tabla.

Por ejemplo, en la fracción decimal 37.051, el dígito 3 está en el lugar de las decenas, 7 está en el lugar de las unidades, 0 está en el lugar de las décimas, 5 está en el lugar de las centésimas y 1 está en el lugar de las milésimas.

Los lugares en fracciones decimales también difieren en precedencia. Si al escribir una fracción decimal nos movemos de dígito en dígito de izquierda a derecha, entonces pasaremos de personas mayores A rangos juveniles. Por ejemplo, el lugar de las centenas es más antiguo que el de las décimas y el lugar de los millones es inferior al de las centésimas. En una fracción decimal final dada, podemos hablar de los dígitos mayores y menores. Por ejemplo, en fracción decimal 604.9387 mayor (más alto) el lugar es el lugar de las centenas, y junior (más bajo)- dígito de diez milésimas.

Para fracciones decimales, se realiza la expansión a dígitos. Es similar a la expansión por dígitos de números naturales. Por ejemplo, la expansión a decimales de 45,6072 es la siguiente: 45,6072=40+5+0,6+0,007+0,0002. Y las propiedades de la suma a partir de la descomposición de una fracción decimal en dígitos le permiten pasar a otras representaciones de esta fracción decimal, por ejemplo, 45,6072=45+0,6072, o 45,6072=40,6+5,007+0,0002, o 45,6072= 45,0072+ 0.6.

Decimales finales

Hasta este punto, solo hemos hablado de fracciones decimales, en cuya notación hay un número finito de dígitos después del punto decimal. Estas fracciones se llaman decimales finitos.

Definición.

Decimales finales- Son fracciones decimales, cuyos registros contienen un número finito de caracteres (dígitos).

A continuación se muestran algunos ejemplos de fracciones decimales finales: 0,317, 3,5, 51,1020304958, 230.032,45.

Sin embargo, no todas las fracciones se pueden representar como un decimal final. Por ejemplo, la fracción 5/13 no se puede sustituir por una fracción igual con uno de los denominadores 10, 100,..., por lo tanto, no se puede convertir en una fracción decimal final. Hablaremos más sobre esto en la sección de teoría, convertir fracciones ordinarias a decimales.

Decimales infinitos: fracciones periódicas y fracciones no periódicas

Al escribir una fracción decimal después del punto decimal, se puede asumir la posibilidad de un número infinito de dígitos. En este caso, pasaremos a considerar las llamadas fracciones decimales infinitas.

Definición.

decimales infinitos- Son fracciones decimales, que contienen un número infinito de dígitos.

Está claro que no podemos escribir infinitas fracciones decimales en su forma completa, por lo que al escribirlas nos limitamos a solo un cierto número finito de dígitos después del punto decimal y ponemos puntos suspensivos que indican una secuencia de dígitos infinitamente continua. A continuación se muestran algunos ejemplos de fracciones decimales infinitas: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….

Si miras de cerca las dos últimas fracciones decimales infinitas, entonces en la fracción 2.111111111... el número 1, que se repite sin cesar, es claramente visible, y en la fracción 69.74152152152..., a partir del tercer decimal, un grupo de números repetidos. 1, 5 y 2 son claramente visibles. Estas fracciones decimales infinitas se llaman periódicas.

Definición.

decimales periódicos(o simplemente fracciones periódicas) son fracciones decimales infinitas, en cuyo registro, a partir de una determinada cifra decimal, se repite infinitamente algún número o grupo de números, lo que se denomina período de la fracción.

Por ejemplo, el período de la fracción periódica 2.111111111... es el dígito 1, y el período de la fracción 69.74152152152... es un grupo de dígitos de la forma 152.

Para fracciones decimales periódicas infinitas se acepta forma especial registros. Para mayor brevedad, acordamos escribir el punto una vez, encerrándolo entre paréntesis. Por ejemplo, la fracción periódica 2.111111111... se escribe como 2,(1) y la fracción periódica 69.74152152152... se escribe como 69.74(152).

Vale la pena señalar que para la misma fracción decimal periódica puedes especificar diferentes periodos. Por ejemplo, la fracción decimal periódica 0,73333... se puede considerar como una fracción 0,7(3) con un periodo de 3, y también como una fracción 0,7(33) con un periodo de 33, y así sucesivamente 0,7(333), 0,7 (3333),... También puedes mirar la fracción periódica 0,73333... así: 0,733(3), o así 0,73(333), etc. Aquí, para evitar ambigüedades y discrepancias, acordamos considerar como período de una fracción decimal la más corta de todas las secuencias posibles de dígitos repetidos, y comenzando desde la posición más cercana a la coma decimal. Es decir, el período de la fracción decimal 0,73333... se considerará una secuencia de un dígito 3, y la periodicidad comienza desde la segunda posición después del punto decimal, es decir, 0,73333...=0,7(3). Otro ejemplo: la fracción periódica 4.7412121212... tiene un periodo de 12, la periodicidad comienza desde el tercer dígito después del punto decimal, es decir, 4.7412121212...=4.74(12).

Las fracciones periódicas decimales infinitas se obtienen convirtiendo en fracciones decimales fracciones ordinarias cuyos denominadores contienen factores primos distintos de 2 y 5.

Aquí cabe mencionar las fracciones periódicas con periodo 9. Demos ejemplos de tales fracciones: 6.43(9) , 27,(9) . Estas fracciones son otra notación para fracciones periódicas con período 0 y, por lo general, se reemplazan por fracciones periódicas con período 0. Para hacer esto, el período 9 se reemplaza por el período 0 y el valor del siguiente dígito más alto se incrementa en uno. Por ejemplo, una fracción con período 9 de la forma 7.24(9) se reemplaza por una fracción periódica con período 0 de la forma 7.25(0) o una fracción decimal final igual 7.25. Otro ejemplo: 4,(9)=5,(0)=5. La igualdad de una fracción con periodo 9 y su correspondiente fracción con periodo 0 se establece fácilmente tras sustituir estas fracciones decimales por fracciones ordinarias iguales.

Finalmente, echemos un vistazo más de cerca a las fracciones decimales infinitas, que no contienen una secuencia de dígitos que se repite sin cesar. Se les llama no periódicos.

Definición.

Decimales no recurrentes(o simplemente fracciones no periódicas) son fracciones decimales infinitas que no tienen punto.

A veces las fracciones no periódicas tienen una forma similar a la de las fracciones periódicas, por ejemplo, 8.02002000200002... es una fracción no periódica. En estos casos, debes tener especial cuidado para notar la diferencia.

Tenga en cuenta que las fracciones no periódicas no se convierten en fracciones ordinarias; las infinitas fracciones decimales no periódicas representan números irracionales.

Operaciones con decimales

Una de las operaciones con fracciones decimales es la comparación, y también están definidas las cuatro funciones aritméticas básicas. operaciones con decimales: suma, resta, multiplicación y división. Consideremos por separado cada una de las acciones con fracciones decimales.

Comparación de decimales basado esencialmente en la comparación de fracciones ordinarias correspondientes a las fracciones decimales que se comparan. Sin embargo, convertir fracciones decimales en fracciones ordinarias es un proceso bastante laborioso y las infinitas fracciones no periódicas no se pueden representar como una fracción ordinaria, por lo que es conveniente utilizar una comparación de fracciones decimales por lugares. La comparación por lugares de fracciones decimales es similar a la comparación de números naturales. Para obtener información más detallada, recomendamos estudiar el artículo: comparación de fracciones decimales, reglas, ejemplos, soluciones.

Movámonos a proxima accion - multiplicar decimales. La multiplicación de fracciones decimales finitas se realiza de manera similar a la resta de fracciones decimales, reglas, ejemplos, soluciones a la multiplicación por una columna de números naturales. En el caso de fracciones periódicas, la multiplicación se puede reducir a la multiplicación de fracciones ordinarias. A su vez, la multiplicación de fracciones decimales infinitas no periódicas después de su redondeo se reduce a la multiplicación de fracciones decimales finitas. Recomendamos para un estudio más profundo el material del artículo: multiplicación de fracciones decimales, reglas, ejemplos, soluciones.

Decimales en un rayo de coordenadas.

Existe una correspondencia uno a uno entre puntos y decimales.

Averigüemos cómo se construyen los puntos en el rayo de coordenadas que corresponden a una fracción decimal dada.

Podemos reemplazar fracciones decimales finitas y fracciones decimales periódicas infinitas con fracciones ordinarias iguales y luego construir las fracciones ordinarias correspondientes en el rayo de coordenadas. Por ejemplo, la fracción decimal 1,4 corresponde a la fracción común 14/10, por lo que el punto con coordenada 1,4 se aleja del origen en dirección positiva 14 segmentos iguales a una décima parte de un segmento unitario.

Las fracciones decimales se pueden marcar en un rayo de coordenadas, a partir de la descomposición de una fracción decimal determinada en dígitos. Por ejemplo, necesitamos construir un punto con la coordenada 16.3007, ya que 16.3007=16+0.3+0.0007, entonces podemos llegar a este punto colocando secuencialmente 16 segmentos unitarios desde el origen de coordenadas, 3 segmentos cuya longitud sea igual a una décima de una unidad, y 7 segmentos, cuya longitud es igual a una diezmilésima parte de un segmento unitario.

Este método de construir números decimales en un rayo de coordenadas le permite acercarse lo más que desee al punto correspondiente a una fracción decimal infinita.

A veces es posible trazar con precisión el punto correspondiente a una fracción decimal infinita. Por ejemplo, , entonces esta fracción decimal infinita 1,41421... corresponde a un punto del rayo de coordenadas, distante del origen de coordenadas por la longitud de la diagonal de un cuadrado de lado 1 segmento unitario.

El proceso inverso de obtener la fracción decimal correspondiente a un punto dado en un rayo de coordenadas es el llamado medida decimal de un segmento. Averigüemos cómo se hace.

Dejemos que nuestra tarea sea llegar desde el origen a un punto dado en la línea de coordenadas (o acercarnos infinitamente si no podemos llegar a él). Con la medida decimal de un segmento, podemos partir secuencialmente del origen cualquier número de segmentos unitarios, luego segmentos cuya longitud sea igual a una décima de unidad, luego segmentos cuya longitud sea igual a una centésima de unidad, etc. Al registrar el número de segmentos de cada longitud apartados, obtenemos la fracción decimal correspondiente a un punto dado del rayo de coordenadas.

Por ejemplo, para llegar al punto M en la figura anterior, es necesario reservar 1 segmento unitario y 4 segmentos, cuya longitud es igual a una décima parte de una unidad. Así, el punto M corresponde a la fracción decimal 1,4.

Está claro que los puntos del rayo de coordenadas que no se pueden alcanzar en el proceso de medición decimal corresponden a infinitas fracciones decimales.

Bibliografía.

• Matemáticas: libro de texto para 5to grado. educación general instituciones / N. Ya Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21ª ed., borrada. - M.: Mnemosyne, 2007. - 280 págs.: enfermo. ISBN 5-346-00699-0.
• Matemáticas. 6to grado: educativo. para educación general instituciones / [N. Ya. Vilenkin y otros]. - 22ª ed., rev. - M.: Mnemosyne, 2008. - 288 p.: enfermo. ISBN 978-5-346-00897-2.
• Álgebra: libro de texto para 8vo grado. educación general instituciones / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editado por S. A. Telyakovsky. - 16ª ed. - M.: Educación, 2008. - 271 p. : enfermo. - ISBN 978-5-09-019243-9.
• Gusev V. A., Mordkovich A. G. Matemáticas (un manual para quienes ingresan a las escuelas técnicas): Proc. asignación.- M.; Más alto escuela, 1984.-351 p., enfermo.

Ya hemos dicho que hay fracciones. común Y decimal. En este momento Hemos estudiado un poco las fracciones. Aprendimos que hay fracciones regulares e impropias. También aprendimos que las fracciones comunes se pueden reducir, sumar, restar, multiplicar y dividir. Y también aprendimos que existen los llamados números mixtos, que constan de un número entero y una parte fraccionaria.

Aún no hemos explorado completamente las fracciones comunes. Hay muchas sutilezas y detalles de los que conviene hablar, pero hoy empezaremos a estudiar. decimal fracciones, ya que a menudo es necesario combinar las fracciones ordinarias y decimales. Es decir, a la hora de resolver problemas hay que utilizar ambos tipos de fracciones.

Esta lección puede parecer complicada y confusa. Es bastante normal. Este tipo de lecciones requieren que se estudien y no se lean superficialmente.

Contenido de la lección

Expresar cantidades en forma fraccionaria

A veces es conveniente mostrar algo en forma fraccionaria. Por ejemplo, una décima parte de un decímetro se escribe así:

Esta expresión significa que un decímetro se dividió en diez partes, y de estas diez partes se tomó una parte:

Como puedes ver en la figura, una décima parte de un decímetro es un centímetro.

Considere el siguiente ejemplo. Muestra 6 cm y otros 3 mm en centímetros en forma fraccionaria.

Entonces, debes expresar 6 cm y 3 mm en centímetros, pero en forma fraccionaria. Ya tenemos 6 centímetros enteros:

pero aún quedan 3 milímetros. ¿Cómo mostrar estos 3 milímetros y en centímetros? Las fracciones vienen al rescate. 3 milímetros es la tercera parte de un centímetro. Y la tercera parte de un centímetro se escribe cm.

Una fracción significa que se dividió un centímetro en diez partes iguales, y de estas diez partes se tomaron tres partes (tres de diez).

Como resultado, tenemos seis centímetros enteros y tres décimas de centímetro:

En este caso, 6 muestra el número de centímetros enteros y la fracción muestra el número de centímetros fraccionarios. Esta fracción se lee como "seis punto tres centímetros".

Las fracciones cuyo denominador contiene los números 10, 100, 1000 se pueden escribir sin denominador. Primero escribe la parte entera y luego el numerador de la parte fraccionaria. La parte entera está separada del numerador de la parte fraccionaria por una coma.

Por ejemplo, escribámoslo sin denominador. Para hacer esto, primero escribamos toda la parte. La parte entera es el número 6. Primero anotamos este número:

Se graba toda la parte. Inmediatamente después de escribir toda la parte ponemos una coma:

Y ahora anotamos el numerador de la parte fraccionaria. En un número mixto, el numerador de la parte fraccionaria es el número 3. Escribimos un tres después de la coma decimal:

Cualquier número que se represente de esta forma se llama decimal.

Por lo tanto, puedes mostrar 6 cm y otros 3 mm en centímetros usando una fracción decimal:

6,3 centímetros

Se verá así:

De hecho, los decimales son lo mismo que las fracciones ordinarias y los números mixtos. La peculiaridad de tales fracciones es que el denominador de su parte fraccionaria contiene los números 10, 100, 1000 o 10000.

Al igual que un número mixto, una fracción decimal tiene una parte entera y una parte fraccionaria. Por ejemplo, en un número mixto la parte entera es 6 y la parte fraccionaria es .

En la fracción decimal 6.3, la parte entera es el número 6 y la parte fraccionaria es el numerador de la fracción, es decir, el número 3.

También sucede que las fracciones ordinarias en cuyo denominador se dan los números 10, 100, 1000 se dan sin parte entera. Por ejemplo, se da una fracción sin una parte entera. Para escribir una fracción como decimal, primero escribe 0, luego pon una coma y escribe el numerador de la fracción. Una fracción sin denominador se escribirá de la siguiente manera:

Lee como "cero punto cinco".

Convertir números mixtos a decimales

Cuando escribimos números mixtos sin denominador, los convertimos a fracciones decimales. Al convertir fracciones a decimales, hay algunas cosas que debes saber, de las que hablaremos ahora.

Después de escribir la parte entera, es necesario contar el número de ceros en el denominador de la parte fraccionaria, ya que el número de ceros de la parte fraccionaria y el número de dígitos después del punto decimal en la fracción decimal deben ser el mismo. ¿Qué significa? Considere el siguiente ejemplo:

En primer lugar

E inmediatamente podrías escribir el numerador de la parte fraccionaria y la fracción decimal estará lista, pero definitivamente necesitas contar el número de ceros en el denominador de la parte fraccionaria.

Entonces, contamos la cantidad de ceros en la parte fraccionaria de un número mixto. El denominador de la parte fraccionaria tiene un cero. Esto significa que en una fracción decimal habrá un dígito después del punto decimal y este dígito será el numerador de la parte fraccionaria del número mixto, es decir, el número 2.

Por lo tanto, cuando se convierte a una fracción decimal, un número mixto se convierte en 3,2.

Esta fracción decimal se lee así:

"Tres punto dos"

“Décimas” porque el número 10 está en la parte fraccionaria de un número mixto.

Ejemplo 2. Convierte un número mixto a decimal.

Escribe toda la parte y pon una coma:

Y podrías escribir inmediatamente el numerador de la parte fraccionaria y obtener la fracción decimal 5,3, pero la regla dice que después del punto decimal debe haber tantos dígitos como ceros en el denominador de la parte fraccionaria de un número mixto. Y vemos que el denominador de la parte fraccionaria tiene dos ceros. Esto significa que nuestra fracción decimal debe tener dos dígitos después del punto decimal, no uno.

En tales casos, es necesario modificar ligeramente el numerador de la parte fraccionaria: agregar un cero antes del numerador, es decir, antes del número 3.

Ahora puedes convertir este número mixto a una fracción decimal. Escribe toda la parte y pon una coma:

Y escribe el numerador de la parte fraccionaria:

La fracción decimal 5.03 se lee de la siguiente manera:

"Cinco coma tres"

“Cientos” porque el denominador de la parte fraccionaria de un número mixto contiene el número 100.

Ejemplo 3. Convierte un número mixto a decimal.

De ejemplos anteriores, aprendimos que para convertir con éxito un número mixto a decimal, la cantidad de dígitos en el numerador de la fracción y la cantidad de ceros en el denominador de la fracción deben ser iguales.

Antes de convertir un número mixto a una fracción decimal, es necesario modificar ligeramente su parte fraccionaria, es decir, para asegurarse de que el número de dígitos en el numerador de la parte fraccionaria y el número de ceros en el denominador de la parte fraccionaria sean los mismos. mismo.

En primer lugar, nos fijamos en el número de ceros en el denominador de la parte fraccionaria. Vemos que hay tres ceros:

Nuestra tarea es organizar tres dígitos en el numerador de la parte fraccionaria. Ya tenemos un dígito: este es el número 2. Queda por agregar dos dígitos más. Serán dos ceros. Súmalos antes del número 2. Como resultado, la cantidad de ceros en el denominador y la cantidad de dígitos en el numerador serán las mismas:

Ahora puedes comenzar a convertir este número mixto a una fracción decimal. Primero anotamos toda la parte y ponemos una coma:

e inmediatamente escribe el numerador de la parte fraccionaria

3,002

Vemos que la cantidad de dígitos después del punto decimal y la cantidad de ceros en el denominador de la parte fraccionaria del número mixto son iguales.

La fracción decimal 3.002 se lee de la siguiente manera:

"Tres coma dos milésimas"

“Milésimas” porque el denominador de la parte fraccionaria del número mixto contiene el número 1000.

Convertir fracciones a decimales

Las fracciones comunes con denominadores de 10, 100, 1000 o 10000 también se pueden convertir a decimales. Como una fracción ordinaria no tiene parte entera, primero escribe 0, luego pon una coma y escribe el numerador de la parte fraccionaria.

Aquí también el número de ceros en el denominador y el número de dígitos en el numerador deben ser iguales. Por lo tanto, debes tener cuidado.

Ejemplo 1.

Falta toda la parte, así que primero escribimos 0 y ponemos una coma:

Ahora miramos el número de ceros en el denominador. Vemos que hay un cero. Y el numerador tiene un dígito. Esto significa que puedes continuar con la fracción decimal de forma segura escribiendo el número 5 después del punto decimal.

En la fracción decimal resultante 0,5, el número de dígitos después del punto decimal y el número de ceros en el denominador de la fracción son los mismos. Esto significa que la fracción se traduce correctamente.

La fracción decimal 0,5 se lee de la siguiente manera:

"Cero punto cinco"

Ejemplo 2. Convertir una fracción a decimal.

Falta una parte entera. Primero escribimos 0 y ponemos una coma:

Ahora miramos el número de ceros en el denominador. Vemos que hay dos ceros. Y el numerador tiene un solo dígito. Para que el número de dígitos y el número de ceros sean iguales, agrega un cero en el numerador antes del número 2. Entonces la fracción tomará la forma . Ahora el número de ceros en el denominador y el número de dígitos en el numerador son los mismos. Entonces puedes continuar con la fracción decimal:

En la fracción decimal resultante 0,02, el número de dígitos después del punto decimal y el número de ceros en el denominador de la fracción son los mismos. Esto significa que la fracción se traduce correctamente.

La fracción decimal 0,02 se lee de la siguiente manera:

"Cero coma dos."

Ejemplo 3. Convertir una fracción a decimal.

Escribe 0 y pon una coma:

Ahora contamos el número de ceros en el denominador de la fracción. Vemos que hay cinco ceros y solo hay un dígito en el numerador. Para que el número de ceros en el denominador y el número de dígitos en el numerador sean iguales, debes agregar cuatro ceros en el numerador antes del número 5:

Ahora el número de ceros en el denominador y el número de dígitos en el numerador son los mismos. Entonces podemos continuar con la fracción decimal. Escribe el numerador de la fracción después del punto decimal.

En la fracción decimal resultante 0,00005, el número de dígitos después del punto decimal y el número de ceros en el denominador de la fracción son los mismos. Esto significa que la fracción se traduce correctamente.

La fracción decimal 0,00005 se lee de la siguiente manera:

“Cero coma quinientas milésimas”.

Convertir fracciones impropias a decimales

Una fracción impropia es una fracción en la que el numerador es mayor que el denominador. Hay fracciones impropias en las que el denominador contiene los números 10, 100, 1000 o 10000. Estas fracciones se pueden convertir a decimales. Pero antes de convertir a una fracción decimal, dichas fracciones deben separarse en la parte entera.

Ejemplo 1.

La fracción es una fracción impropia. Para convertir dicha fracción a decimal, primero debes seleccionar la parte completa. Recordemos cómo aislar la parte entera de fracciones impropias. Si lo has olvidado, te aconsejamos que vuelvas a estudiarlo.

Entonces, resaltemos la parte entera en la fracción impropia. Recuerde que una fracción significa división - en en este caso dividiendo el número 112 por el número 10

Miremos esta imagen y armemos un nuevo número mixto, como un juego de construcción para niños. El número 11 será la parte entera, el número 2 será el numerador de la parte fraccionaria y el número 10 será el denominador de la parte fraccionaria.

Tenemos un número mixto. Convirtámoslo a una fracción decimal. Y ya sabemos cómo convertir esos números a fracciones decimales. Primero, escribe toda la parte y pon una coma:

Ahora contamos el número de ceros en el denominador de la parte fraccionaria. Vemos que hay un cero. Y el numerador de la parte fraccionaria tiene un dígito. Esto significa que la cantidad de ceros en el denominador de la parte fraccionaria y la cantidad de dígitos en el numerador de la parte fraccionaria son iguales. Esto nos da la oportunidad de escribir inmediatamente el numerador de la parte fraccionaria después del punto decimal:

En la fracción decimal resultante 11.2, el número de dígitos después del punto decimal y el número de ceros en el denominador de la fracción son los mismos. Esto significa que la fracción se traduce correctamente.

Esto significa que una fracción impropia se convierte en 11,2 cuando se convierte a decimal.

La fracción decimal 11.2 se lee de la siguiente manera:

"Once punto dos."

Ejemplo 2. Convertir fracción impropia a decimal.

Es una fracción impropia porque el numerador es mayor que el denominador. Pero se puede convertir a una fracción decimal, ya que el denominador contiene el número 100.

En primer lugar, seleccionemos la parte completa de esta fracción. Para hacer esto, divida 450 por 100 con una esquina:

Recopilemos un nuevo número mixto: obtenemos . Y ya sabemos cómo convertir números mixtos a fracciones decimales.

Escribe toda la parte y pon una coma:

Ahora contamos la cantidad de ceros en el denominador de la parte fraccionaria y la cantidad de dígitos en el numerador de la parte fraccionaria. Vemos que la cantidad de ceros en el denominador y la cantidad de dígitos en el numerador son iguales. Esto nos da la oportunidad de escribir inmediatamente el numerador de la parte fraccionaria después del punto decimal:

En la fracción decimal resultante 4,50, el número de dígitos después del punto decimal y el número de ceros en el denominador de la fracción son los mismos. Esto significa que la fracción se traduce correctamente.

Esto significa que una fracción impropia se convierte en 4,50 cuando se convierte a decimal.

Al resolver problemas, si hay ceros al final de la fracción decimal, se pueden descartar. También eliminemos el cero en nuestra respuesta. Entonces obtenemos 4,5

Ésta es una de las cosas interesantes de los decimales. Consiste en que los ceros que aparecen al final de una fracción no le dan ningún peso a esta fracción. En otras palabras, los decimales 4,50 y 4,5 son iguales. Pongamos un signo igual entre ellos:

4,50 = 4,5

Surge la pregunta: ¿por qué sucede esto? Después de todo, 4,50 y 4,5 parecen fracciones diferentes. Todo el secreto reside en la propiedad básica de las fracciones, que estudiamos anteriormente. Intentaremos demostrar por qué las fracciones decimales 4,50 y 4,5 son iguales, pero después de estudiar el siguiente tema, que se llama "convertir una fracción decimal en un número mixto".

Convertir un decimal a un número mixto

Cualquier fracción decimal se puede convertir nuevamente en un número mixto. Para ello, basta con saber leer fracciones decimales. Por ejemplo, convierta 6,3 a un número mixto. 6,3 es seis punto tres. Primero escribimos seis números enteros:

y junto a tres décimas:

Ejemplo 2. Convertir decimal 3.002 a número mixto

3,002 es tres enteros y dos milésimas. Primero escribimos tres números enteros.

y al lado escribimos dos milésimas:

Ejemplo 3. Convertir decimal 4,50 a número mixto

4,50 son cuatro coma cincuenta. Escribe cuatro números enteros.

y los siguientes cincuenta centésimos:

Por cierto, recordemos el último ejemplo del tema anterior. Dijimos que los decimales 4,50 y 4,5 son iguales. También dijimos que el cero se puede descartar. Intentemos demostrar que los decimales 4,50 y 4,5 son iguales. Para ello convertimos ambas fracciones decimales en números mixtos.

Cuando se convierte a un número mixto, el decimal 4,50 se convierte en y el decimal 4,5 se convierte en

Tenemos dos números mixtos y . Convertimos estos números mixtos a fracciones impropias:

Ahora tenemos dos fracciones y . Es hora de recordar la propiedad básica de una fracción, que dice que cuando multiplicas (o divides) el numerador y el denominador de una fracción por el mismo número, el valor de la fracción no cambia.

Dividamos la primera fracción por 10.

Obtuvimos , y esta es la segunda fracción. Esto significa que ambos son iguales entre sí e iguales al mismo valor:

Intente usar una calculadora para dividir primero 450 entre 100 y luego 45 entre 10. Será algo divertido.

Convertir una fracción decimal a una fracción

Cualquier fracción decimal se puede convertir nuevamente en una fracción. Para ello, de nuevo, basta con saber leer fracciones decimales. Por ejemplo, convierta 0,3 a una fracción común. 0,3 es cero coma tres. Primero escribimos cero números enteros:

y junto a tres décimas 0. Tradicionalmente, el cero no se escribe, por lo que la respuesta final no será 0, sino simplemente .

Ejemplo 2. Convierte la fracción decimal 0,02 a una fracción.

0,02 es cero coma dos. No escribimos cero, por lo que inmediatamente escribimos dos centésimas.

Ejemplo 3. Convertir 0,00005 a fracción

0,00005 es cero coma cinco. No escribimos cero, por lo que inmediatamente escribimos quinientas milésimas

¿Te gustó la lección?
Únase a nuestro nuevo grupo VKontakte y comience a recibir notificaciones sobre nuevas lecciones