Que ya son bastante aburridos. Y siento que ha llegado el momento de extraer nuevas conservas de las reservas estratégicas de la teoría. ¿Es posible expandir la función a una serie de alguna otra manera? Por ejemplo, ¿expresar un segmento de línea recta en términos de senos y cosenos? Parece increíble, pero funciones tan aparentemente lejanas pueden ser
"reunificación". Además de los títulos familiares en teoría y práctica, existen otros enfoques para expandir una función en una serie.
En esta lección aprenderemos sobre trigonometría. cerca de Fourier, tocaremos el tema de su convergencia y suma y, por supuesto, analizaremos numerosos ejemplos de expansión de funciones en una serie de Fourier. Sinceramente quería titular el artículo “Serie de Fourier para tontos”, pero sería falso, ya que resolver los problemas requeriría conocimiento de otras ramas del análisis matemático y algo de experiencia práctica. Por lo tanto, el preámbulo se parecerá al entrenamiento de astronautas =)
En primer lugar, el estudio de los materiales de las páginas debe abordarse en excelente forma. Somnoliento, descansado y sobrio. Sin emociones fuertes por la pata rota de un hámster y pensamientos obsesivos sobre las dificultades de la vida peces de acuario. Sin embargo, la serie de Fourier no es difícil de entender. tareas practicas simplemente requieren una mayor concentración de atención; lo ideal es desconectarse por completo de los estímulos externos. La situación se ve agravada por el hecho de que no existe una manera sencilla de comprobar la solución y la respuesta. Por lo tanto, si su salud está por debajo del promedio, entonces es mejor hacer algo más simple. Es verdad.
En segundo lugar, antes de volar al espacio es necesario estudiar el panel de instrumentos. astronave. Comencemos con los valores de las funciones en las que se debe hacer clic en la máquina:
Para cualquier valor natural:
1). De hecho, la sinusoide "cose" el eje x a través de cada "pi":
. En el caso de valores negativos del argumento, el resultado, por supuesto, será el mismo: .
2). Pero no todos lo sabían. El coseno "pi" es el equivalente a una "intermitente":
Un argumento negativo no cambia la cuestión: 
.
Quizás eso sea suficiente.
Y en tercer lugar, querido cuerpo de cosmonautas, debéis ser capaces de... integraros.
En particular, subsumir con confianza una función bajo el signo diferencial, integrarla por partes y estar en armonía con la fórmula de Newton-Leibniz. Comencemos los importantes ejercicios previos al vuelo. No recomiendo categóricamente omitirlo para no aplastarlo más tarde en la ingravidez:
Ejemplo 1
Calcular integrales definidas
donde toma los valores naturales.
Solución: la integración se realiza sobre la variable “x” y en esta etapa la variable discreta “en” se considera constante. En todas las integrales subsumimos la función bajo el signo diferencial:
Una versión corta de la solución a la que sería bueno apuntar se ve así:
Acostumbrémonos:
Los cuatro puntos restantes corren por tu cuenta. Intenta abordar la tarea concienzudamente y escribe las integrales de forma breve. Soluciones de muestra al final de la lección.
Después de realizar los ejercicios CALIDAD, nos ponemos trajes espaciales.
¡Y preparándonos para empezar!
Consideremos alguna función que esté definida al menos en un intervalo (y, posiblemente, en un intervalo mayor). Si esta función es integrable en el intervalo, entonces se puede expandir a una serie trigonométrica de Fourier: 
, donde están los llamados coeficientes de Fourier.
En este caso, el número se llama período de descomposición y el número se llama medio período de descomposición.
Es obvio que en el caso general la serie de Fourier consta de senos y cosenos: 
De hecho, vamos a anotarlo en detalle:
El término cero de la serie suele escribirse en la forma.
Los coeficientes de Fourier se calculan mediante las siguientes fórmulas: 
Entiendo perfectamente que quienes empiezan a estudiar el tema aún no tienen claros los nuevos términos: periodo de descomposición, medio ciclo, coeficientes de Fourier etc. Que no cunda el pánico, esto no es comparable a la emoción antes de ir al espacio exterior. Entendamos todo en el siguiente ejemplo, antes de ejecutarlo es lógico plantearse preguntas prácticas urgentes:
¿Qué necesitas hacer en las siguientes tareas?Expande la función a una serie de Fourier. Además, a menudo es necesario representar la gráfica de una función, la gráfica de la suma de una serie, una suma parcial y, en el caso de fantasías docentes sofisticadas, hacer otra cosa.
¿Cómo expandir una función a una serie de Fourier?Básicamente, necesitas encontrar coeficientes de Fourier, es decir, componer y calcular tres integrales definidas.
Copie la forma general de la serie de Fourier y las tres fórmulas de trabajo en su cuaderno. Me alegro mucho de que algunos visitantes del sitio estén haciendo realidad su sueño de la infancia de convertirse en astronautas ante mis ojos =)
Ejemplo 2
Expande la función a una serie de Fourier en el intervalo. Construye una gráfica, una gráfica de la suma de la serie y la suma parcial.
Solución: la primera parte de la tarea es expandir la función a una serie de Fourier.
El comienzo es estándar, asegúrese de anotarlo:
En este problema, el período de expansión es medio período.
Expandamos la función a una serie de Fourier en el intervalo: 
Usando las fórmulas apropiadas, encontramos coeficientes de Fourier. Ahora necesitas componer y calcular tres integrales definidas. Por conveniencia, enumeraré los puntos:
1) La primera integral es la más simple, sin embargo, también requiere ojos: 
2) Utilice la segunda fórmula:
Esta integral es bien conocida y se toma en partes: 
Al realizar la búsqueda se utilizó el método de subsumir la función bajo el signo diferencial.
En el problema considerado, es más conveniente utilizar inmediatamente la fórmula de integración por partes en una integral definida. 
:
Un par de notas técnicas. En primer lugar, después de aplicar la fórmula, toda la expresión debe estar entre paréntesis grandes, ya que hay una constante delante de la integral original. ¡No la perdamos! Los paréntesis se pueden ampliar en cualquier paso posterior; lo hice como último recurso. En la primera "pieza" 
Ponemos mucho cuidado en la sustitución, como se puede ver, no se utiliza la constante y se sustituyen los límites de integración en el producto. Esta acción está resaltada entre corchetes. Bueno, ya conoces la integral de la segunda “parte” de la fórmula de la tarea de entrenamiento;-)
Y lo más importante: ¡concentración extrema!
3) Buscamos el tercer coeficiente de Fourier:
Se obtiene una relativa a la integral anterior, que también se puede integrar por partes: 
Este caso es un poco más complicado, comentaré los siguientes pasos paso a paso: 
(1) Encerramos la expresión completa entre corchetes grandes. No quería parecer aburrido, pierden la constante con demasiada frecuencia.
(2) V en este caso Inmediatamente abrí esos grandes corchetes. Atención especial Nos dedicamos a la primera “pieza”: la constante fuma al margen y no participa en la sustitución de los límites de integración ( y ) en el producto. Debido al desorden del registro, nuevamente es aconsejable resaltar esta acción entre corchetes. Con la segunda "pieza" 
todo es más simple: aquí la fracción apareció después de abrir paréntesis grandes, y la constante, como resultado de integrar la integral familiar;-)
(3) Entre corchetes realizamos transformaciones, y en la integral derecha - sustitución de límites de integración.
(4) Quitamos la “luz intermitente” de los corchetes:, y luego abrimos los corchetes interiores:.
(5) Cancelamos 1 y –1 entre paréntesis y hacemos simplificaciones finales.
Finalmente, se encuentran los tres coeficientes de Fourier: 
Sustituyémoslos en la fórmula. 
:
Al mismo tiempo, no olvides dividir por la mitad. En el último paso, la constante (“menos dos”), que no depende de “en”, se saca de la suma.
Así, hemos obtenido la expansión de la función en una serie de Fourier en el intervalo: 
Estudiemos la cuestión de la convergencia de la serie de Fourier. Explicaré la teoría, en particular. teorema de dirichlet, literalmente "en los dedos", por lo que si necesita formulaciones estrictas, consulte el libro de texto sobre Análisis matemático (por ejemplo, el segundo volumen de Bohan; o el tercer volumen de Fichtenholtz, pero es más difícil).
La segunda parte del problema requiere dibujar una gráfica, una gráfica de la suma de una serie y una gráfica de una suma parcial.
La gráfica de la función es una línea recta ordinaria en el plano, que se dibuja con una línea de puntos negra: 
Averigüemos la suma de la serie. Como sabes, las series de funciones convergen en funciones. En nuestro caso, la serie de Fourier construida 
para cualquier valor de "x" convergerá a la función, que se muestra en rojo. Esta función sufre discontinuidades de 1er tipo en los puntos, pero también está definido en ellos (puntos rojos en el dibujo)
De este modo: 
. Es fácil ver que es notablemente diferente de la función original, por eso en la entrada 
Se utiliza una tilde en lugar de un signo igual.
Estudiemos un algoritmo que sea conveniente para construir la suma de una serie.
En el intervalo central, la serie de Fourier converge con la función misma (el segmento rojo central coincide con la línea de puntos negra de la función lineal).
Ahora hablemos un poco sobre la naturaleza de la expansión trigonométrica que estamos considerando. series de Fourier 
incluye solo funciones periódicas (constantes, senos y cosenos), por lo que la suma de la serie 
También es una función periódica.
¿Qué significa esto en nuestro ejemplo específico? Y esto significa que la suma de la serie 
– es ciertamente periódico y el segmento rojo del intervalo debe repetirse sin cesar a izquierda y derecha.
Creo que el significado de la frase “período de descomposición” finalmente ha quedado claro. En pocas palabras, cada vez la situación se repite una y otra vez.
En la práctica suele ser suficiente representar tres períodos de descomposición, como se muestra en el dibujo. Bueno, y también los "muñones" de los períodos vecinos, para que quede claro que el gráfico continúa.
De particular interés son los puntos de discontinuidad del primer tipo. En tales puntos, la serie de Fourier converge a valores aislados, que se encuentran exactamente en el medio del "salto" de la discontinuidad (puntos rojos en el dibujo). ¿Cómo saber la ordenada de estos puntos? Primero, encontremos la ordenada del “piso superior”: para ello, calculamos el valor de la función en el punto más a la derecha del período central de la expansión: . Para calcular la ordenada del “piso inferior” la forma más sencilla es tomar el extremo valor izquierdo del mismo periodo: 
. La ordenada del valor promedio es la media aritmética de la suma de “arriba y abajo”: . Un hecho agradable es que al construir un dibujo, verá inmediatamente si el medio se calculó correctamente o incorrectamente.
Construyamos una suma parcial de la serie y al mismo tiempo repitamos el significado del término "convergencia". El motivo también se conoce por la lección sobre la suma de una serie de números. Describamos nuestra riqueza en detalle:
Para componer una suma parcial, debes escribir cero + dos términos más de la serie. Eso es,
El dibujo muestra la gráfica de la función. verde, y, como puede ver, "envuelve" la cantidad total con bastante fuerza. Si consideramos una suma parcial de cinco términos de la serie, entonces la gráfica de esta función se aproximará aún más exactamente a las líneas rojas; si hay cien términos, entonces la "serpiente verde" en realidad se fusionará completamente con los segmentos rojos, etc. Por tanto, la serie de Fourier converge a su suma.
Es interesante notar que cualquier suma parcial es una función continua, pero la suma total de la serie sigue siendo discontinua.
En la práctica, no es tan raro construir un gráfico de suma parcial. ¿Cómo hacerlo? En nuestro caso, es necesario considerar la función en el segmento, calcular sus valores en los extremos del segmento y en los puntos intermedios (cuantos más puntos considere, más precisa será la gráfica). Luego, debes marcar estos puntos en el dibujo y dibujar cuidadosamente un gráfico en el período, y luego "replicarlo" en intervalos adyacentes. ¿De que otra forma? Después de todo, la aproximación también es una función periódica... ...en cierto modo su gráfico me recuerda a un ritmo cardíaco uniforme en la pantalla de un dispositivo médico.
Realizar la construcción, por supuesto, no es muy conveniente, ya que hay que tener mucho cuidado, manteniendo una precisión de al menos medio milímetro. Sin embargo, complaceré a los lectores que no se sienten cómodos dibujando: en un problema "real" no siempre es necesario realizar un dibujo; en aproximadamente el 50% de los casos es necesario expandir la función a una serie de Fourier y eso es todo. .
Después de completar el dibujo, completamos la tarea:
Respuesta : 
En muchos problemas, la función sufre una discontinuidad de 1er tipo justo en el período de expansión:
Ejemplo 3
Expande la función dada en el intervalo a una serie de Fourier. Dibuja una gráfica de la función y la suma total de la serie.
La función propuesta se especifica por partes. (y, nota, solo en el segmento) y sufre una discontinuidad de 1º tipo en el punto . ¿Es posible calcular los coeficientes de Fourier? Ningún problema. Tanto el lado izquierdo como el derecho de la función son integrables en sus intervalos, por lo tanto, las integrales en cada una de las tres fórmulas deben representarse como la suma de dos integrales. Veamos, por ejemplo, cómo se hace esto para un coeficiente cero:
La segunda integral resultó ser igual a cero, lo que redujo el trabajo, pero no siempre es así.
Los otros dos coeficientes de Fourier se describen de manera similar.
¿Cómo mostrar la suma de una serie? En el intervalo de la izquierda dibujamos un segmento de línea recta, y en el intervalo, un segmento de línea recta (resaltamos la sección del eje en negrita y negrita). Es decir, en el intervalo de expansión, la suma de la serie coincide con la función en todas partes excepto en tres puntos "malos". En el punto de discontinuidad de la función, la serie de Fourier convergerá a un valor aislado, que se ubica exactamente en el medio del “salto” de la discontinuidad. No es difícil verlo oralmente: límite del lado izquierdo:, límite del lado derecho: 
y, obviamente, la ordenada del punto medio es 0,5.
Debido a la periodicidad de la suma, la imagen debe "multiplicarse" en períodos adyacentes, en particular, lo mismo debe representarse en los intervalos y . Al mismo tiempo, en los puntos la serie de Fourier convergerá a los valores medianos.
De hecho, no hay nada nuevo aquí.
Intente hacer frente a esta tarea usted mismo. Una muestra aproximada del diseño final y un dibujo al final de la lección.
Expansión de una función a una serie de Fourier durante un período arbitrarioPara un período de expansión arbitrario, donde "el" es cualquier número positivo, las fórmulas para la serie de Fourier y los coeficientes de Fourier se distinguen por un argumento un poco más complicado para el seno y el coseno:
Si , entonces obtenemos las fórmulas de intervalo con las que comenzamos.
El algoritmo y los principios para resolver el problema se conservan por completo, pero aumenta la complejidad técnica de los cálculos:
Ejemplo 4
Expande la función a una serie de Fourier y traza la suma. 
Solución: en realidad un análogo del Ejemplo No. 3 con una discontinuidad del primer tipo en el punto. En este problema, el período de expansión es medio período. La función se define sólo en el medio intervalo, pero esto no cambia el asunto: es importante que ambas partes de la función sean integrables.
Ampliemos la función a una serie de Fourier:
Dado que la función es discontinua en el origen, cada coeficiente de Fourier obviamente debe escribirse como la suma de dos integrales:
1) Escribiré la primera integral con el mayor detalle posible:
2) Observamos atentamente la superficie de la Luna:
Tomamos la segunda integral por partes: 
¿A qué debemos prestar mucha atención después de abrir la continuación de la solución con un asterisco?
En primer lugar, no perdemos la primera integral. 
, donde inmediatamente aplicamos el signo diferencial. En segundo lugar, no olvide la constante desafortunada antes de los corchetes grandes y no se confunda con los signos al usar la fórmula. 
. Es aún más conveniente abrir los soportes grandes inmediatamente en el siguiente paso.
El resto es cuestión de técnica; las dificultades sólo pueden deberse a una experiencia insuficiente en la resolución de integrales.
Sí, no en vano los eminentes colegas del matemático francés Fourier se indignaron: ¡¿cómo se atrevió a ordenar funciones en series trigonométricas?! =) Por cierto, probablemente todo el mundo esté interesado en el significado práctico de la tarea en cuestión. El propio Fourier trabajó en modelo matemático La conductividad térmica, y posteriormente la serie que lleva su nombre, comenzaron a utilizarse para estudiar muchos procesos periódicos que son visibles e invisibles en el mundo circundante. Ahora, por cierto, me sorprendí pensando que no fue por casualidad que comparé la gráfica del segundo ejemplo con el ritmo periódico del corazón. Los interesados pueden familiarizarse con la aplicación práctica. Transformada de Fourier en fuentes de terceros. ...Aunque es mejor no hacerlo, será recordado como el primer amor =)
3) Teniendo en cuenta los eslabones débiles mencionados repetidamente, veamos el tercer coeficiente:
Integramos por partes: 
Sustituyamos los coeficientes de Fourier encontrados en la fórmula. 
, sin olvidar dividir el coeficiente cero por la mitad:
Tracemos la suma de la serie. Repitamos brevemente el procedimiento: construimos una línea recta en un intervalo y una línea recta en un intervalo. Si el valor de “x” es cero, ponemos un punto en medio del “salto” de la brecha y “replicamos” el gráfico para períodos adyacentes: 
En las “cruces” de períodos, la suma también será igual a los puntos medios del “salto” de la brecha.
Listo. Permítanme recordarles que la función en sí, por condición, está definida solo en un medio intervalo y, obviamente, coincide con la suma de la serie en los intervalos.
Respuesta :
A veces, una función dada por partes es continua durante el período de expansión. El ejemplo más simple: 
. Solución (ver Bohan volumen 2) Lo mismo que en los dos ejemplos anteriores: a pesar de la continuidad de la función en el punto, cada coeficiente de Fourier se expresa como la suma de dos integrales.
En el intervalo de expansión, puede haber más puntos de discontinuidad de 1er tipo y/o puntos “conjuntos” del gráfico (dos, tres y generalmente cualquier final cantidad). Si una función es integrable en cada parte, entonces también es expandible en una serie de Fourier. Pero por experiencia práctica no recuerdo algo tan cruel. Sin embargo, hay tareas más difíciles que las que acabamos de considerar, y al final del artículo hay enlaces a series de Fourier de mayor complejidad para todos.
Mientras tanto, relajémonos, recuéstese en nuestros asientos y contemplemos las infinitas extensiones de estrellas:
Ejemplo 5
Expande la función a una serie de Fourier en el intervalo y traza la suma de la serie.
En este problema, la función es continua en el medio intervalo de la expansión, lo que simplifica la solución. Todo es muy similar al Ejemplo No. 2. No hay forma de escapar de la nave espacial; tendrás que decidir =) Se adjunta una muestra de diseño aproximada al final de la lección y un cronograma.
Expansión en serie de Fourier de funciones pares e imparesCon funciones pares e impares, el proceso de resolución del problema se simplifica notablemente. Y es por eso. Volvamos al desarrollo de una función en una serie de Fourier con un período de “dos pi” 
y periodo arbitrario “dos el” 
.
Supongamos que nuestra función es par. El término general de la serie, como puedes ver, contiene cosenos pares y senos impares. Y si estamos expandiendo una función PAR, ¿por qué necesitamos senos impares? Restablezcamos el coeficiente innecesario: .
Por tanto, una función par se puede expandir a una serie de Fourier sólo en cosenos: 
Dado que las integrales de funciones pares sobre un segmento de integración simétrico con respecto a cero se pueden duplicar, los coeficientes de Fourier restantes también se simplifican.
Para la brecha: 
Para un intervalo arbitrario: 
Los ejemplos de libros de texto que se pueden encontrar en casi cualquier libro de texto sobre análisis matemático incluyen expansiones de funciones pares. 
. Además, los he encontrado varias veces en mi práctica personal:
Ejemplo 6
La función está dada. Requerido:
1) expandir la función a una serie de Fourier con período , donde es un número positivo arbitrario;
2) escribir el desarrollo del intervalo, construir una función y graficar la suma total de la serie.
Solución: en el primer párrafo se propone resolver el problema en vista general¡Y es muy conveniente! Si surge la necesidad, simplemente sustituya su valor.
1) En este problema, el período de expansión es medio período. Durante otras acciones, en particular durante la integración, "el" se considera una constante
La función es par, lo que significa que se puede expandir a una serie de Fourier sólo en cosenos: 
.
Buscamos coeficientes de Fourier usando las fórmulas. 
. Preste atención a sus ventajas incondicionales. En primer lugar, la integración se realiza sobre el segmento positivo de la expansión, lo que significa que nos deshacemos del módulo de forma segura. 
, considerando sólo la “X” de las dos piezas. Y, en segundo lugar, la integración se simplifica notablemente.
Dos: 
Integramos por partes:
De este modo:
, mientras que la constante , que no depende de “en”, se saca de la suma.
Respuesta : 
2) Escribamos la expansión en el intervalo, para ello en formula general sustituto valor deseado medio ciclo:
Las series de Fourier son una representación de una función arbitraria con un período específico en forma de serie. En general, esta solución se denomina descomposición de un elemento sobre una base ortogonal. La expansión de funciones en series de Fourier es una herramienta bastante poderosa para resolver diversos problemas debido a las propiedades de esta transformación durante la integración, diferenciación y cambio de expresiones por argumento y convolución.
Una persona que no esté familiarizada con las matemáticas superiores, así como con los trabajos del científico francés Fourier, probablemente no entenderá qué son estas "series" y para qué sirven. Mientras tanto, esta transformación se ha integrado bastante en nuestras vidas. Lo utilizan no sólo los matemáticos, sino también los físicos, químicos, médicos, astrónomos, sismólogos, oceanógrafos y muchos otros. Echemos un vistazo más de cerca a los trabajos del gran científico francés que hizo un descubrimiento adelantado a su tiempo.
El hombre y la transformada de FourierLas series de Fourier son uno de los métodos (junto con el análisis y otros) Este proceso ocurre cada vez que una persona escucha un sonido. Nuestro oído realiza automáticamente la transformación. partículas elementales en un medio elástico se disponen en filas (a lo largo del espectro) de valores sucesivos de niveles de sonoridad para tonos de diferentes alturas. Luego, el cerebro convierte estos datos en sonidos que nos resultan familiares. Todo esto sucede sin nuestro deseo o conciencia, por sí solo, pero para comprender estos procesos será necesario estudiar matemáticas superiores durante varios años.
La transformada de Fourier se puede realizar mediante métodos analíticos, numéricos y otros. Las series de Fourier se refieren al método numérico de descomponer cualquier proceso oscilatorio, desde las mareas oceánicas y las ondas de luz hasta los ciclos de actividad solar (y otros objetos astronómicos). Con estas técnicas matemáticas, puede analizar funciones que representan cualquier proceso oscilatorio como una serie de componentes sinusoidales que se mueven del mínimo al máximo y viceversa. La transformada de Fourier es una función que describe la fase y amplitud de las sinusoides correspondientes a una frecuencia específica. Este proceso se puede utilizar para resolver ecuaciones muy complejas que describen procesos dinámicos que surgen bajo la influencia de energía térmica, luminosa o eléctrica. Además, las series de Fourier permiten aislar componentes constantes en señales oscilatorias complejas, lo que permite interpretar correctamente las observaciones experimentales obtenidas en medicina, química y astronomía.
El padre fundador de esta teoría es el matemático francés Jean Baptiste Joseph Fourier. Posteriormente, esta transformación recibió su nombre. Inicialmente, el científico utilizó su método para estudiar y explicar los mecanismos de la conductividad térmica: la propagación del calor en sólidos. Fourier sugirió que la distribución irregular inicial se puede descomponer en sinusoides simples, cada una de las cuales tendrá su propia temperatura mínima y máxima, así como su propia fase. En este caso, cada uno de estos componentes se medirá desde el mínimo hasta el máximo y viceversa. La función matemática que describe los picos superior e inferior de la curva, así como la fase de cada uno de los armónicos, se denomina transformada de Fourier de la expresión de distribución de temperatura. El autor de la teoría reunió. función general distribución, que es difícil de describir matemáticamente, a una serie muy conveniente de coseno y seno, que juntos dan la distribución original.
El principio de transformación y las opiniones de los contemporáneos.Los contemporáneos del científico, destacados matemáticos de principios del siglo XIX, no aceptaron esta teoría. La principal objeción fue la afirmación de Fourier de que una función discontinua, que describe una línea recta o una curva discontinua, puede representarse como una suma de expresiones sinusoidales que son continuas. Como ejemplo, consideremos el paso de Heaviside: su valor es cero a la izquierda de la discontinuidad y uno a la derecha. Esta función describe la dependencia de la corriente eléctrica de una variable temporal cuando el circuito está cerrado. Los contemporáneos de la teoría en ese momento nunca se habían encontrado con una situación similar en la que una expresión discontinua pudiera describirse mediante una combinación de funciones ordinarias continuas como exponencial, seno, lineal o cuadrática.
Después de todo, si el matemático tenía razón en sus afirmaciones, entonces al sumar la serie trigonométrica infinita de Fourier, se puede obtener una representación precisa de la expresión del paso, incluso si tiene muchos pasos similares. A principios del siglo XIX semejante afirmación parecía absurda. Pero a pesar de todas las dudas, muchos matemáticos ampliaron el alcance del estudio de este fenómeno, llevándolo más allá del estudio de la conductividad térmica. Sin embargo, la mayoría de los científicos seguían atormentados por la pregunta: "¿Puede la suma de una serie sinusoidal converger a valor exacto función discontinua?
Convergencia de series de Fourier: un ejemploLa cuestión de la convergencia surge siempre que es necesario sumar series infinitas de números. Para comprender este fenómeno, consideremos un ejemplo clásico. ¿Podrás llegar alguna vez a la pared si cada paso posterior tiene la mitad del tamaño del anterior? Digamos que estás a dos metros de tu objetivo, el primer paso te lleva a la mitad del camino, el siguiente te lleva a los tres cuartos y después del quinto habrás cubierto casi el 97 por ciento del camino. Sin embargo, no importa cuántos pasos dé, no logrará el objetivo previsto en un sentido matemático estricto. Utilizando cálculos numéricos, se puede demostrar que eventualmente es posible acercarse a una distancia determinada. Esta prueba equivale a demostrar que la suma de un medio, un cuarto, etc. tenderá a la unidad.
Esta cuestión volvió a plantearse a finales del siglo XIX, cuando se intentó utilizar series de Fourier para predecir la intensidad de las mareas. En ese momento, Lord Kelvin inventó un dispositivo que era analógico dispositivo informático, lo que permitió a marineros militares y de la marina mercante rastrear este fenómeno natural. Este mecanismo determinó conjuntos de fases y amplitudes a partir de una tabla de alturas de marea y puntos temporales correspondientes, medidos cuidadosamente en un puerto determinado durante todo el año. Cada parámetro era un componente sinusoidal de la expresión de la altura de la marea y era uno de los componentes regulares. Las mediciones se introdujeron en el instrumento de cálculo de Lord Kelvin, que sintetizó una curva que predijo la altura del agua en función del tiempo para el año siguiente. Muy pronto se trazaron curvas similares para todos los puertos del mundo.
¿Qué pasa si el proceso se ve interrumpido por una función discontinua?En aquel momento parecía obvio que un predictor de maremotos con un gran número de elementos de conteo podía calcular un gran número de fases y amplitudes y así proporcionar predicciones más precisas. Sin embargo, resultó que este patrón no se observa en los casos en que la expresión de marea que debía sintetizarse contenía un salto brusco, es decir, era discontinua. Si se introducen en el dispositivo datos de una tabla de momentos de tiempo, éste calcula varios coeficientes de Fourier. La función original se restablece gracias a los componentes sinusoidales (de acuerdo con los coeficientes encontrados). La discrepancia entre la expresión original y la reconstruida se puede medir en cualquier punto. Al realizar repetidos cálculos y comparaciones, queda claro que el valor del error mayor no disminuye. Sin embargo, están localizados en la región correspondiente al punto de discontinuidad y en cualquier otro punto tienden a cero. En 1899, este resultado fue confirmado teóricamente por Joshua Willard Gibbs de la Universidad de Yale.
El análisis de Fourier no es aplicable a expresiones que contienen un número infinito de picos en un intervalo determinado. En general, las series de Fourier, si la función original está representada por el resultado del real dimensión física, siempre convergen. Las preguntas sobre la convergencia de este proceso para clases específicas de funciones llevaron al surgimiento de nuevas ramas de las matemáticas, por ejemplo, la teoría de funciones generalizadas. Se la asocia con nombres como L. Schwartz, J. Mikusinski y J. Temple. En el marco de esta teoría, una clara y precisa bases teóricas bajo expresiones como la función delta de Dirac (describe una región de un área única concentrada en una vecindad infinitesimal de un punto) y el “paso” de Heaviside. Gracias a este trabajo, las series de Fourier se volvieron aplicables para resolver ecuaciones y problemas que involucran conceptos intuitivos: carga puntual, masa puntual, dipolos magnéticos y carga concentrada en una viga.
método de fourierLas series de Fourier, de acuerdo con los principios de interferencia, comienzan con la descomposición de formas complejas en otras más simples. Por ejemplo, un cambio en el flujo de calor se explica por su paso a través de varios obstáculos hechos de material aislante térmico de forma irregular o un cambio en la superficie de la tierra: un terremoto, un cambio de órbita. cuerpo celestial- influencia de los planetas. Como regla general, las ecuaciones que describen sistemas clásicos simples se pueden resolver fácilmente para cada onda individual. Fourier demostró que soluciones simples También se pueden sumar para obtener soluciones a problemas más complejos. En términos matemáticos, las series de Fourier son una técnica para representar una expresión como una suma de armónicos: coseno y seno. Es por eso este análisis También conocido como análisis armónico.
Series de Fourier: una técnica ideal antes de la "era de las computadoras"Antes de la creación equipo de computadora La técnica de Fourier fue la mejor arma en el arsenal de los científicos cuando trabajaban con la naturaleza ondulatoria de nuestro mundo. series de Fourier forma compleja te permite decidir no sólo tareas simples, que son susceptibles de la aplicación directa de las leyes de la mecánica de Newton, pero también de ecuaciones fundamentales. La mayoría de los descubrimientos de la ciencia newtoniana en el siglo XIX fueron posibles únicamente gracias a la técnica de Fourier.
Con el desarrollo de las computadoras, las transformadas de Fourier han alcanzado un nivel cualitativamente nuevo. Esta técnica está firmemente establecida en casi todas las áreas de la ciencia y la tecnología. Un ejemplo es el audio y el vídeo digitales. Su implementación sólo fue posible gracias a una teoría desarrollada por un matemático francés a principios del siglo XIX. Así, la serie de Fourier en una forma compleja hizo posible un gran avance en el estudio del espacio exterior. Además, influyó en el estudio de la física de materiales semiconductores y plasma, acústica de microondas, oceanografía, radar y sismología.
Serie trigonométrica de FourierEn matemáticas, una serie de Fourier es una forma de representar arbitrarios funciones complejas la suma de otros más simples. EN casos generales el número de tales expresiones puede ser infinito. Además, cuanto más se tenga en cuenta su número en el cálculo, más preciso será el resultado final. Se utiliza con mayor frecuencia como protozoos. funciones trigonométricas coseno o seno. En este caso, las series de Fourier se llaman trigonométricas y la solución de tales expresiones se llama expansión armónica. Este método juega papel importante en matemáticas. En primer lugar, la serie trigonométrica proporciona un medio para representar y estudiar funciones; es el aparato principal de la teoría. Además, te permite resolver una serie de problemas de física matemática. Finalmente, esta teoría contribuyó al desarrollo y dio vida a una serie de secciones muy importantes. ciencia matemática(teoría de integrales, teoría de funciones periódicas). Además, sirvió como punto de partida para el desarrollo de las siguientes funciones de una variable real y también sentó las bases para el análisis armónico.
Serie de Fourier de funciones periódicas con período 2π.
La serie de Fourier nos permite estudiar funciones periódicas descomponiéndolas en componentes. Son típicos las corrientes y voltajes alternos, los desplazamientos, la velocidad y aceleración de los mecanismos de manivela y las ondas acústicas. ejemplos prácticos Aplicación de funciones periódicas en cálculos de ingeniería.
La expansión de la serie de Fourier se basa en el supuesto de que todas las funciones de importancia práctica en el intervalo -π ≤x≤ π pueden expresarse en forma de series trigonométricas convergentes (una serie se considera convergente si la secuencia de sumas parciales compuesta por sus términos converge):
Notación estándar (=ordinaria) mediante la suma de senx y cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
donde a o, a 1,a 2,...,b 1,b 2,.. son constantes reales, es decir
Donde, para el rango de -π a π, los coeficientes de la serie de Fourier se calculan mediante las fórmulas:
Los coeficientes a o , a n y b n se denominan coeficientes de Fourier y, si se pueden encontrar, entonces la serie (1) se denomina serie de Fourier correspondiente a la función f (x). Para la serie (1), el término (a 1 cosx+b 1 senx) se llama primer armónico o fundamental,
Otra forma de escribir una serie es usar la relación acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Donde a o es una constante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 son las amplitudes de las distintas componentes, y es igual a a n =arctg a n /b n.
Para la serie (1), el término (a 1 cosx+b 1 sinx) o c 1 sin(x+α 1) se llama primer armónico o fundamental, (a 2 cos2x+b 2 sin2x) o c 2 sin(2x +α 2) llamado segundo armónico y así sucesivamente.
Para representar con precisión una señal compleja normalmente se requiere un número infinito de términos. Sin embargo, en muchos problemas prácticos es suficiente considerar sólo los primeros términos.
Serie de Fourier de funciones no periódicas con período 2π.
Ampliación de funciones no periódicas.
Si la función f(x) no es periódica, significa que no se puede expandir a una serie de Fourier para todos los valores de x. Sin embargo, es posible definir una serie de Fourier que represente una función en cualquier rango de ancho 2π.
Dada una función no periódica, se puede construir una nueva función seleccionando valores de f(x) dentro de un cierto rango y repitiéndolos fuera de ese rango en intervalos de 2π. Dado que la nueva función es periódica con período 2π, se puede expandir a una serie de Fourier para todos los valores de x. Por ejemplo, la función f(x)=x no es periódica. Sin embargo, si es necesario expandirlo a una serie de Fourier en el intervalo de o a 2π, entonces fuera de este intervalo se construye una función periódica con un período de 2π (como se muestra en la figura siguiente).
Para funciones no periódicas como f(x)=x, la suma de la serie de Fourier es igual al valor de f(x) en todos los puntos de un rango determinado, pero no es igual a f(x) para los puntos fuera del rango. Para encontrar la serie de Fourier de una función no periódica en el rango 2π, se utiliza la misma fórmula de los coeficientes de Fourier.
Funciones pares e impares.
Dicen que una función y=f(x) es par si f(-x)=f(x) para todos los valores de x. Las gráficas de funciones pares siempre son simétricas con respecto al eje y (es decir, son imágenes especulares). Dos ejemplos de funciones pares: y=x2 e y=cosx.
Se dice que una función y=f(x) es impar si f(-x)=-f(x) para todos los valores de x. Las gráficas de funciones impares siempre son simétricas con respecto al origen.
Muchas funciones no son ni pares ni impares.
Desarrollo en series de Fourier en cosenos.
La serie de Fourier de una función periódica par f(x) con período 2π contiene sólo términos cosenos (es decir, no hay términos senos) y puede incluir un término constante. Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
La serie de Fourier de una función periódica impar f(x) con periodo 2π contiene sólo términos con senos (es decir, no contiene términos con cosenos).
Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
Serie de Fourier en medio ciclo.
Si una función se define para un rango, digamos de 0 a π, y no sólo de 0 a 2π, se puede expandir en una serie sólo en senos o sólo en cosenos. La serie de Fourier resultante se llama serie de Fourier de medio ciclo.
Si desea obtener una expansión de Fourier de medio ciclo de los cosenos de la función f(x) en el rango de 0 a π, entonces necesita construir una función periódica par. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Porque el incluso función Simétrica con respecto al eje f(x), dibuje la línea AB, como se muestra en la figura. abajo. Si suponemos que fuera del intervalo considerado el resultado obtenido forma triangular es periódica con un período de 2π, entonces se ve la gráfica final, como se muestra. en la Fig. abajo. Como necesitamos obtener el desarrollo de Fourier en cosenos, como antes, calculamos los coeficientes de Fourier a o y a n
Si desea obtener una expansión de Fourier de medio ciclo en términos de los senos de la función f(x) en el rango de 0 a π, entonces necesita construir una función periódica impar. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función impar es simétrica con respecto al origen, construimos la recta CD, como se muestra en la figura. Si asumimos que fuera del intervalo considerado la señal en diente de sierra resultante es periódica con un período de 2π, entonces la gráfica final tiene la forma que se muestra en la Fig. Como necesitamos obtener la expansión de Fourier del semiciclo en términos de senos, como antes, calculamos el coeficiente de Fourier. b
Serie de Fourier para un intervalo arbitrario.
Expansión de una función periódica con periodo L.
La función periódica f(x) se repite cuando x aumenta en L, es decir f(x+L)=f(x). La transición de las funciones consideradas anteriormente con un período de 2π a funciones con un período de L es bastante simple, ya que se puede realizar mediante un cambio de variable.
Para encontrar la serie de Fourier de la función f(x) en el rango -L/2≤x≤L/2, introducimos una nueva variable u para que la función f(x) tenga un período de 2π con respecto a u. Si u=2πx/L, entonces x=-L/2 para u=-π y x=L/2 para u=π. También dejemos f(x)=f(Lu/2π)=F(u). La serie de Fourier F(u) tiene la forma
(Los límites de integración se pueden reemplazar por cualquier intervalo de longitud L, por ejemplo, de 0 a L)
Serie de Fourier en medio ciclo para funciones especificadas en el intervalo L≠2π.
Para la sustitución u=πх/L, el intervalo de x=0 a x=L corresponde al intervalo de u=0 a u=π. En consecuencia, la función se puede expandir en una serie solo en cosenos o solo en senos, es decir en una serie de Fourier en medio ciclo.
La expansión del coseno en el rango de 0 a L tiene la forma
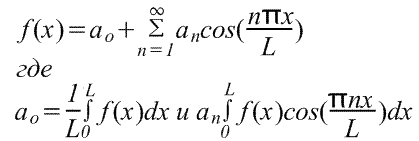
Funciones, descomponiéndolas en componentes. Las corrientes y voltajes alternos, los desplazamientos, la velocidad y aceleración de los mecanismos de manivela y las ondas acústicas son ejemplos prácticos típicos del uso de funciones periódicas en los cálculos de ingeniería.
La expansión de la serie de Fourier se basa en el supuesto de que todas las funciones de importancia práctica en el intervalo -π ≤x≤ π pueden expresarse en forma de series trigonométricas convergentes (una serie se considera convergente si la secuencia de sumas parciales compuesta por sus términos converge):
Notación estándar (=ordinaria) mediante la suma de senx y cosxf(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
donde a o, a 1,a 2,...,b 1,b 2,.. son constantes reales, es decir
Donde, para el rango de -π a π, los coeficientes de la serie de Fourier se calculan mediante las fórmulas:
Los coeficientes a o , a n y b n se denominan coeficientes de Fourier y, si se pueden encontrar, entonces la serie (1) se denomina serie de Fourier correspondiente a la función f (x). Para la serie (1), el término (a 1 cosx+b 1 senx) se llama primer armónico o fundamental,
Otra forma de escribir una serie es usar la relación acosx+bsinx=csin(x+α)f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Donde a o es una constante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 son las amplitudes de las distintas componentes, y es igual a a n =arctg a n /b n.
Para la serie (1), el término (a 1 cosx+b 1 sinx) o c 1 sin(x+α 1) se llama primer armónico o fundamental, (a 2 cos2x+b 2 sin2x) o c 2 sin(2x +α 2) llamado segundo armónico y así sucesivamente.
Para representar con precisión una señal compleja normalmente se requiere un número infinito de términos. Sin embargo, en muchos problemas prácticos es suficiente considerar sólo los primeros términos.
Serie de Fourier de funciones no periódicas con período 2π. Ampliación de funciones no periódicas a series de Fourier.Si la función f(x) no es periódica, significa que no se puede expandir a una serie de Fourier para todos los valores de x. Sin embargo, es posible definir una serie de Fourier que represente una función en cualquier rango de ancho 2π.
Dada una función no periódica, se puede construir una nueva función seleccionando valores de f(x) dentro de un cierto rango y repitiéndolos fuera de ese rango en intervalos de 2π. Dado que la nueva función es periódica con período 2π, se puede expandir a una serie de Fourier para todos los valores de x. Por ejemplo, la función f(x)=x no es periódica. Sin embargo, si es necesario expandirlo a una serie de Fourier en el intervalo de o a 2π, entonces fuera de este intervalo se construye una función periódica con un período de 2π (como se muestra en la figura siguiente).
Para funciones no periódicas como f(x)=x, la suma de la serie de Fourier es igual al valor de f(x) en todos los puntos de un rango determinado, pero no es igual a f(x) para los puntos fuera del rango. Para encontrar la serie de Fourier de una función no periódica en el rango 2π, se utiliza la misma fórmula de los coeficientes de Fourier.
Funciones pares e impares.Dicen que una función y=f(x) es par si f(-x)=f(x) para todos los valores de x. Las gráficas de funciones pares siempre son simétricas con respecto al eje y (es decir, son imágenes especulares). Dos ejemplos de funciones pares: y=x2 e y=cosx.
Se dice que una función y=f(x) es impar si f(-x)=-f(x) para todos los valores de x. Las gráficas de funciones impares siempre son simétricas con respecto al origen.
Muchas funciones no son ni pares ni impares.
Desarrollo en series de Fourier en cosenos.La serie de Fourier de una función periódica par f(x) con período 2π contiene sólo términos cosenos (es decir, no hay términos senos) y puede incluir un término constante. Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
La serie de Fourier de una función periódica impar f(x) con periodo 2π contiene sólo términos con senos (es decir, no contiene términos con cosenos).
Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
Si una función se define para un rango, digamos de 0 a π, y no sólo de 0 a 2π, se puede expandir en una serie sólo en senos o sólo en cosenos. La serie de Fourier resultante se llama serie de Fourier de medio ciclo.
Si desea obtener una expansión de Fourier de medio ciclo de los cosenos de la función f(x) en el rango de 0 a π, entonces necesita construir una función periódica par. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función par es simétrica con respecto al eje f(x), trazamos la línea AB, como se muestra en la figura. abajo. Si asumimos que fuera del intervalo considerado la forma triangular resultante es periódica con un período de 2π, entonces el gráfico final se ve así: en la Fig. abajo. Como necesitamos obtener el desarrollo de Fourier en cosenos, como antes, calculamos los coeficientes de Fourier a o y a n
Si desea obtener funciones f(x) en el rango de 0 a π, entonces necesita construir una función periódica impar. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función impar es simétrica con respecto al origen, construimos la recta CD, como se muestra en la figura. Si asumimos que fuera del intervalo considerado la señal en diente de sierra resultante es periódica con un período de 2π, entonces la gráfica final tiene la forma que se muestra en la Fig. Como necesitamos obtener la expansión de Fourier del semiciclo en términos de senos, como antes, calculamos el coeficiente de Fourier. b
Expansión de una función periódica con periodo L.
La función periódica f(x) se repite cuando x aumenta en L, es decir f(x+L)=f(x). La transición de las funciones consideradas anteriormente con un período de 2π a funciones con un período de L es bastante simple, ya que se puede realizar mediante un cambio de variable.
Para encontrar la serie de Fourier de la función f(x) en el rango -L/2≤x≤L/2, introducimos una nueva variable u para que la función f(x) tenga un período de 2π con respecto a u. Si u=2πx/L, entonces x=-L/2 para u=-π y x=L/2 para u=π. También dejemos f(x)=f(Lu/2π)=F(u). La serie de Fourier F(u) tiene la forma
¿Dónde están los coeficientes de la serie de Fourier?
Sin embargo, lo más frecuente es que la fórmula anterior resulte en una dependencia de x. Dado que u=2πx/L, significa du=(2π/L)dx, y los límites de integración son de -L/2 a L/2 en lugar de - π a π. En consecuencia, la serie de Fourier para la dependencia de x tiene la forma
donde en el rango de -L/2 a L/2 están los coeficientes de la serie de Fourier,
(Los límites de integración se pueden reemplazar por cualquier intervalo de longitud L, por ejemplo, de 0 a L)
Serie de Fourier en medio ciclo para funciones especificadas en el intervalo L≠2π.Para la sustitución u=πх/L, el intervalo de x=0 a x=L corresponde al intervalo de u=0 a u=π. En consecuencia, la función se puede expandir en una serie solo en cosenos o solo en senos, es decir en una serie de Fourier en medio ciclo.
La expansión del coseno en el rango de 0 a L tiene la forma
como insertar fórmulas matemáticas al sitio web?
Si alguna vez necesita agregar una o dos fórmulas matemáticas a una página web, la forma más sencilla de hacerlo es como se describe en el artículo: las fórmulas matemáticas se insertan fácilmente en el sitio en forma de imágenes que Wolfram Alpha genera automáticamente. . Además de la simplicidad, este método universal ayudará a mejorar la visibilidad del sitio en los motores de búsqueda. Ha estado funcionando durante mucho tiempo (y creo que funcionará para siempre), pero ya está moralmente desactualizado.
Si utiliza fórmulas matemáticas con regularidad en su sitio, le recomiendo que utilice MathJax, una biblioteca especial de JavaScript que muestra notación matemática en navegadores web utilizando el marcado MathML, LaTeX o ASCIIMathML.
Hay dos formas de comenzar a usar MathJax: (1) usando un código simple, puede conectar rápidamente un script MathJax a su sitio web, que se cargará automáticamente desde un servidor remoto en el momento adecuado (lista de servidores); (2) descargue el script MathJax desde un servidor remoto a su servidor y conéctelo a todas las páginas de su sitio. El segundo método, más complejo y que requiere más tiempo, acelerará la carga de las páginas de su sitio, y si el servidor principal MathJax deja de estar disponible temporalmente por algún motivo, esto no afectará su propio sitio de ninguna manera. A pesar de estas ventajas, elegí el primer método porque es más sencillo, más rápido y no requiere conocimientos técnicos. Siga mi ejemplo y en solo 5 minutos podrá utilizar todas las funciones de MathJax en su sitio.
Puede conectar el script de la biblioteca MathJax desde un servidor remoto usando dos opciones de código tomadas del sitio web principal de MathJax o de la página de documentación:
Una de estas opciones de código debe copiarse y pegarse en el código de su página web, preferiblemente entre etiquetas o inmediatamente después de la etiqueta. Según la primera opción, MathJax se carga más rápido y ralentiza menos la página. Pero la segunda opción monitorea y carga automáticamente las últimas versiones de MathJax. Si inserta el primer código, deberá actualizarlo periódicamente. Si inserta el segundo código, las páginas se cargarán más lentamente, pero no necesitará monitorear constantemente las actualizaciones de MathJax.
La forma más sencilla de conectar MathJax es en Blogger o WordPress: en el panel de control del sitio, agregue un widget diseñado para insertar código JavaScript de terceros, copie la primera o segunda versión del código de descarga presentado anteriormente y coloque el widget más cerca. al principio de la plantilla (por cierto, esto no es necesario en absoluto, ya que el script MathJax se carga de forma asincrónica). Eso es todo. Ahora aprenda la sintaxis de marcado de MathML, LaTeX y ASCIIMathML y estará listo para insertar fórmulas matemáticas en las páginas web de su sitio.
Cualquier fractal se construye de acuerdo con una determinada regla, que se aplica secuencialmente un número ilimitado de veces. Cada uno de esos momentos se denomina iteración.
El algoritmo iterativo para construir una esponja de Menger es bastante simple: el cubo original de lado 1 se divide por planos paralelos a sus caras en 27 cubos iguales. Se eliminan un cubo central y 6 cubos adyacentes a lo largo de las caras. El resultado es un conjunto formado por los 20 cubos más pequeños restantes. Haciendo lo mismo con cada uno de estos cubos, obtenemos un conjunto formado por 400 cubos más pequeños. Siguiendo este proceso hasta el infinito, obtenemos una esponja de Menger.
