Consideraremos expresiones de la serie de Fourier en forma trigonométrica y compleja, y también prestaremos atención a las condiciones de Dirichlet para la convergencia de la serie de Fourier. Además, nos detendremos en detalle en la explicación de un concepto como la frecuencia negativa del espectro de una señal, que a menudo plantea dificultades a la hora de familiarizarse con la teoría del análisis espectral.
Señal periódica. Serie trigonométrica de Fourier
Sea una señal periódica de tiempo continuo que se repite con un período c, es decir , donde es un número entero arbitrario.
Como ejemplo, la Figura 1 muestra una secuencia de pulsos rectangulares de duración c, repetidos con un período de c.
Figura 1. Secuencia periódica
pulsos rectangulares
Del curso de análisis matemático se sabe que el sistema de funciones trigonométricas
Con múltiples frecuencias, donde rad/s es un número entero, forma una base ortonormal para la descomposición de señales periódicas con un período que satisface las condiciones de Dirichlet. Las condiciones de Dirichlet para la convergencia de la serie de Fourier requieren que se especifique una señal periódica en el segmento y se cumplan las siguientes condiciones:
Por ejemplo, la función periódica 
no satisface las condiciones de Dirichlet porque la función tiene discontinuidades del segundo tipo y toma valores infinitos en , donde es un número entero arbitrario. Entonces la función no puede ser representado cerca de Fourier. También puedes dar un ejemplo de la función. 
, que es limitado, pero tampoco satisface las condiciones de Dirichlet, ya que tiene un número infinito de puntos extremos cuando se acerca a cero. Gráfica de una función se muestra en la Figura 2.
Figura 2. Gráfico de funciones :
a - dos períodos de repetición; b - en las proximidades
La figura 2a muestra dos períodos de repetición de la función. , y en la Figura 2b - el área cercana a . Se puede ver que a medida que se acerca a cero, la frecuencia de oscilación aumenta infinitamente y dicha función no puede representarse mediante una serie de Fourier, porque no es monótona por partes.
Cabe señalar que en la práctica no existen señales con valores infinitos de corriente o voltaje. Funciones con un número infinito de extremos de tipo. Tampoco ocurren en problemas aplicados. Todas las señales periódicas reales satisfacen las condiciones de Dirichlet y pueden representarse mediante una serie trigonométrica infinita de Fourier de la forma:
En la expresión (2), el coeficiente especifica el componente constante de la señal periódica.
En todos los puntos donde la señal es continua, la serie de Fourier (2) converge a los valores de la señal dada, y en puntos de discontinuidad del primer tipo, al valor promedio, donde y son los límites a la izquierda y a la derecha del punto de discontinuidad, respectivamente.
También se sabe por el análisis matemático que el uso de una serie de Fourier truncada, que contiene sólo los primeros términos en lugar de una suma infinita, conduce a una representación aproximada de la señal:
En el cual se garantiza el error cuadrático medio mínimo. La Figura 3 ilustra la aproximación de un tren de ondas cuadradas periódicas y una onda de rampa periódica cuando se utilizan diferentes números de términos de la serie de Fourier.
Figura 3. Aproximación de señales mediante una serie de Fourier truncada:
a - pulsos rectangulares; b - señal de diente de sierra
Serie de Fourier en forma compleja
En la sección anterior, examinamos la serie trigonométrica de Fourier para la expansión de una señal periódica arbitraria que satisface las condiciones de Dirichlet. Usando la fórmula de Euler, podemos demostrar:
Luego la serie trigonométrica de Fourier (2) teniendo en cuenta (4):
Por lo tanto, una señal periódica se puede representar mediante la suma de un componente constante y exponenciales complejos que giran en frecuencias con coeficientes para frecuencias positivas y exponenciales complejos que giran en frecuencias negativas.
Consideremos los coeficientes para exponenciales complejos que giran con frecuencias positivas:
De manera similar, los coeficientes para exponenciales complejos que giran con frecuencias negativas son:
Las expresiones (6) y (7) coinciden; además, la componente constante también se puede escribir mediante una exponencial compleja a frecuencia cero:
Por lo tanto, (5) teniendo en cuenta (6)-(8) se puede representar como una suma única cuando se indexa desde menos infinito hasta infinito:
De la expresión (2) se deduce que para una señal real los coeficientes de la serie (2) también son reales. Sin embargo, (9) asocia una señal real con un conjunto de coeficientes conjugados complejos relacionados con frecuencias positivas y negativas.
Algunas explicaciones de la serie de Fourier en forma compleja
En la sección anterior hicimos la transición de la serie trigonométrica de Fourier (2) a la serie de Fourier en forma compleja (9). Como resultado, en lugar de descomponer señales periódicas en base a funciones trigonométricas reales, obtuvimos una expansión en base a exponenciales complejas, con coeficientes complejos, ¡e incluso aparecieron frecuencias negativas en la expansión! Dado que esta cuestión a menudo se malinterpreta, es necesaria alguna aclaración.
Primero, trabajar con exponentes complejos es en la mayoría de los casos más fácil que trabajar con funciones trigonométricas. Por ejemplo, al multiplicar y dividir exponentes complejos, basta con sumar (restar) los exponentes, mientras que las fórmulas para multiplicar y dividir funciones trigonométricas son más engorrosas.
Diferenciar e integrar exponenciales, incluso los complejos, también es más fácil que las funciones trigonométricas, que cambian constantemente cuando se derivan e integran (el seno se convierte en coseno y viceversa).
Si la señal es periódica y real, entonces la serie trigonométrica de Fourier (2) parece más clara, porque todos los coeficientes de expansión , y siguen siendo reales. Sin embargo, a menudo hay que trabajar con señales periódicas complejas (por ejemplo, al modular y demodular, se utiliza una representación en cuadratura de la envolvente compleja). En este caso, cuando se usa la serie trigonométrica de Fourier, todos los coeficientes y expansiones (2) se volverán complejos, mientras que cuando se usa la serie de Fourier en forma compleja (9), se usarán los mismos coeficientes de expansión para señales de entrada tanto reales como complejas. .
Y finalmente, es necesario detenerse en la explicación de las frecuencias negativas que aparecieron en (9). Esta pregunta suele provocar malentendidos. EN La vida cotidiana no encontramos frecuencias negativas. Por ejemplo, nunca sintonizamos nuestra radio en una frecuencia negativa. Consideremos la siguiente analogía de la mecánica. Sea un péndulo de resorte mecánico que oscile libremente con una frecuencia determinada. ¿Puede un péndulo oscilar con una frecuencia negativa? Por supuesto que no. Así como no existen estaciones de radio que transmitan en frecuencias negativas, la frecuencia de las oscilaciones de un péndulo no puede ser negativa. Pero un péndulo de resorte es un objeto unidimensional (el péndulo oscila a lo largo de una línea recta).
También podemos dar otra analogía de la mecánica: una rueda que gira con una frecuencia de . La rueda, a diferencia del péndulo, gira, es decir. un punto en la superficie de la rueda se mueve en un plano y no oscila simplemente a lo largo de una línea recta. Por lo tanto, para especificar de forma única la rotación de la rueda, no basta con establecer la velocidad de rotación, ya que también es necesario establecer la dirección de rotación. Precisamente por eso podemos utilizar el signo de frecuencia.
Entonces, si la rueda gira con una frecuencia angular rad/s en el sentido contrario a las agujas del reloj, entonces consideramos que la rueda gira con una frecuencia positiva, y si en el sentido de las agujas del reloj, entonces la frecuencia de rotación será negativa. Así, para un comando de rotación, una frecuencia negativa deja de ser una tontería e indica el sentido de rotación.
Y ahora lo más importante que debemos entender. La oscilación de un objeto unidimensional (por ejemplo, un péndulo de resorte) se puede representar como la suma de las rotaciones de dos vectores que se muestran en la Figura 4.
Figura 4. Oscilación de un péndulo de resorte.
como la suma de rotaciones de dos vectores
en el plano complejo
El péndulo oscila a lo largo del eje real del plano complejo con una frecuencia según la ley armónica. El movimiento del péndulo se muestra como un vector horizontal. El vector superior gira en el plano complejo con una frecuencia positiva (en el sentido contrario a las agujas del reloj) y el vector inferior gira con una frecuencia negativa (en el sentido de las agujas del reloj). La Figura 4 ilustra claramente la conocida relación del curso de trigonometría:
Así, la serie de Fourier en forma compleja (9) representa señales unidimensionales periódicas como una suma de vectores en el plano complejo que giran con frecuencias positivas y negativas. Al mismo tiempo, observemos que en el caso de una señal real, según (9), los coeficientes de expansión para frecuencias negativas son conjugados complejos con los coeficientes correspondientes para frecuencias positivas. En el caso de una señal compleja, esta propiedad de los coeficientes no se cumple debido a que y también son complejos.
Espectro de señales periódicas.
La serie de Fourier en forma compleja es la descomposición de una señal periódica en una suma de exponenciales complejas que giran a frecuencias positivas y negativas en múltiplos de rad/c con los correspondientes coeficientes complejos que determinan el espectro de la señal. Los coeficientes complejos se pueden representar usando la fórmula de Euler como, donde es el espectro de amplitud, a es el espectro de fase.
Dado que las señales periódicas se disponen en fila solo en una cuadrícula de frecuencia fija, el espectro de señales periódicas es lineal (discreto).
Figura 5. Espectro de una secuencia periódica
pulsos rectangulares:
a - espectro de amplitud; b - espectro de fases
La Figura 5 muestra un ejemplo del espectro de amplitud y fase de una secuencia periódica de pulsos rectangulares (ver Figura 1) en c, duración del pulso c y amplitud del pulso B.
Serie de Fourier de funciones periódicas con período 2π.
La serie de Fourier nos permite estudiar funciones periódicas descomponiéndolas en componentes. Son típicos las corrientes y voltajes alternos, los desplazamientos, la velocidad y aceleración de los mecanismos de manivela y las ondas acústicas. ejemplos prácticos Aplicación de funciones periódicas en cálculos de ingeniería.
La expansión de la serie de Fourier se basa en el supuesto de que todas las funciones de importancia práctica en el intervalo -π ≤x≤ π pueden expresarse en forma de series trigonométricas convergentes (una serie se considera convergente si la secuencia de sumas parciales compuesta por sus términos converge):
Notación estándar (=ordinaria) mediante la suma de senx y cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
donde a o, a 1,a 2,...,b 1,b 2,.. son constantes reales, es decir
Donde, para el rango de -π a π, los coeficientes de la serie de Fourier se calculan mediante las fórmulas:
Los coeficientes a o , a n y b n se llaman coeficientes de Fourier, y si se pueden encontrar, entonces la serie (1) se llama junto a Fourier, correspondiente a la función f(x). Para la serie (1), el término (a 1 cosx+b 1 senx) se llama primero o armónico fundamental,
Otra forma de escribir una serie es usar la relación acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Donde a o es una constante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 son las amplitudes de las distintas componentes, y es igual a a n =arctg a n /b n.
Para la serie (1), el término (a 1 cosx+b 1 sinx) o c 1 sin(x+α 1) se llama primero o armónico fundamental,(a 2 cos2x+b 2 sin2x) o c 2 sin(2x+α 2) se llama segundo armónico etcétera.
Para representar con precisión una señal compleja normalmente se requiere un número infinito de términos. Sin embargo, en muchos problemas prácticos es suficiente considerar sólo los primeros términos.
Serie de Fourier de funciones no periódicas con período 2π.
Ampliación de funciones no periódicas.
Si la función f(x) no es periódica, significa que no se puede expandir a una serie de Fourier para todos los valores de x. Sin embargo, es posible definir una serie de Fourier que represente una función en cualquier rango de ancho 2π.
Dada una función no periódica, se puede construir una nueva función seleccionando valores de f(x) dentro de un cierto rango y repitiéndolos fuera de ese rango en intervalos de 2π. Dado que la nueva función es periódica con período 2π, se puede expandir a una serie de Fourier para todos los valores de x. Por ejemplo, la función f(x)=x no es periódica. Sin embargo, si es necesario expandirlo a una serie de Fourier en el intervalo de o a 2π, entonces fuera de este intervalo se construye una función periódica con un período de 2π (como se muestra en la figura siguiente).
Para funciones no periódicas como f(x)=x, la suma de la serie de Fourier es igual al valor de f(x) en todos los puntos en un rango dado, pero no es igual a f(x) para los puntos fuera del rango. Para encontrar la serie de Fourier de una función no periódica en el rango 2π, se utiliza la misma fórmula de los coeficientes de Fourier.
Funciones pares e impares.
Dicen que la función y=f(x) incluso, si f(-x)=f(x) para todos los valores de x. Las gráficas de funciones pares siempre son simétricas con respecto al eje y (es decir, son imágenes especulares). Dos ejemplos de funciones pares: y=x2 e y=cosx.
Dicen que la función y=f(x) extraño, si f(-x)=-f(x) para todos los valores de x. Las gráficas de funciones impares siempre son simétricas con respecto al origen.
Muchas funciones no son ni pares ni impares.
Desarrollo en series de Fourier en cosenos.
La serie de Fourier de una función periódica par f(x) con período 2π contiene sólo términos cosenos (es decir, no hay términos senos) y puede incluir un término constante. Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
La serie de Fourier de una función periódica impar f(x) con periodo 2π contiene sólo términos con senos (es decir, no contiene términos con cosenos).
Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
Serie de Fourier en medio ciclo.
Si una función se define para un rango, digamos de 0 a π, y no sólo de 0 a 2π, se puede expandir en una serie sólo en senos o sólo en cosenos. La serie de Fourier resultante se llama cerca de Fourier a medio ciclo.
Si quieres obtener la descomposición. Fourier de medio ciclo por cosenos funciones f(x) en el rango de 0 a π, entonces es necesario construir una función periódica par. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Porque el incluso función Simétrica con respecto al eje f(x), dibuje la línea AB, como se muestra en la figura. abajo. Si suponemos que fuera del intervalo considerado el resultado obtenido forma triangular es periódica con un período de 2π, entonces se ve la gráfica final, como se muestra. en la Fig. abajo. Como necesitamos obtener el desarrollo de Fourier en cosenos, como antes, calculamos los coeficientes de Fourier a o y a n
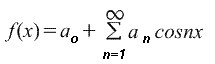
Si necesitas conseguir Expansión seno de medio ciclo de Fourier funciones f(x) en el rango de 0 a π, entonces es necesario construir una función periódica impar. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función impar es simétrica con respecto al origen, construimos la recta CD, como se muestra en la figura. Si asumimos que fuera del intervalo considerado la señal en diente de sierra resultante es periódica con un período de 2π, entonces la gráfica final tiene la forma que se muestra en la Fig. Como necesitamos obtener la expansión de Fourier del semiciclo en términos de senos, como antes, calculamos el coeficiente de Fourier. b
Serie de Fourier para un intervalo arbitrario.
Expansión de una función periódica con período L.
función periódica f(x) se repite cuando x aumenta en L, es decir f(x+L)=f(x). La transición de las funciones previamente consideradas con un período de 2π a funciones con un período de L es bastante simple, ya que se puede realizar mediante un cambio de variable.
Para encontrar la serie de Fourier de la función f(x) en el rango -L/2≤x≤L/2, introducimos una nueva variable u para que la función f(x) tenga un período de 2π con respecto a u. Si u=2πx/L, entonces x=-L/2 para u=-π y x=L/2 para u=π. También dejemos f(x)=f(Lu/2π)=F(u). La serie de Fourier F(u) tiene la forma
(Los límites de integración se pueden reemplazar por cualquier intervalo de longitud L, por ejemplo, de 0 a L)
Serie de Fourier en medio ciclo para funciones especificadas en el intervalo L≠2π.
Para la sustitución u=πх/L, el intervalo de x=0 a x=L corresponde al intervalo de u=0 a u=π. En consecuencia, la función se puede expandir en una serie solo en cosenos o solo en senos, es decir V Serie de Fourier en medio ciclo..
La expansión del coseno en el rango de 0 a L tiene la forma
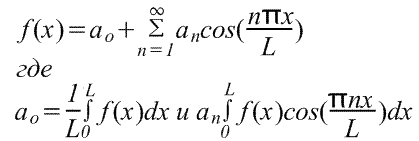
, Dónde
.
La serie de Fourier de una función f(x) en el intervalo (-l;l) es una serie trigonométrica de la forma: 
, Dónde
.
Objetivo. Calculadora online está diseñado para expandir la función f(x) en una serie de Fourier.
Para funciones de módulo (como |x|), utilice expansión del coseno.
Reglas para ingresar funciones.:
Para funciones de módulo, utilice la expansión del coseno. Por ejemplo, para |x| es necesario ingresar una función sin módulo, es decir X.Serie de Fourier continua por partes, monótona por partes y acotada en el intervalo (- yo;yo) de la función converge en toda la recta numérica.
Suma de la serie de Fourier S(x) :
- es una función periódica con periodo 2 yo. Una función u(x) se llama periódica con período T (o T-periódica) si para todo x de la región R, u(x+T)=u(x).
- en el intervalo (- yo;yo) coincide con la función F(X), excepto para los puntos de interrupción
- en puntos de discontinuidad (del primer tipo, ya que la función está acotada) de la función F(X) y al final del intervalo toma valores medios:
Dicen que la función se expande en una serie de Fourier en el intervalo (- yo;yo):
.
Si F(X) es una función par, entonces sólo las funciones pares participan en su expansión, es decir bn=0.
Si F(X) es una función impar, entonces sólo las funciones impares participan en su expansión, es decir y N=0
Cerca de Fourier
funciones F(X) en el intervalo (0; yo) por cosenos de múltiples arcos
la fila se llama: 
, Dónde 
.
Cerca de Fourier
funciones F(X) en el intervalo (0; yo) a lo largo de los senos de múltiples arcos
la fila se llama: 
, Dónde 
.
La suma de la serie de Fourier sobre los cosenos de múltiples arcos es una función periódica par con período 2 yo, coincidiendo con F(X) en el intervalo (0; yo) en puntos de continuidad.
La suma de la serie de Fourier sobre los senos de múltiples arcos es una función periódica impar con período 2 yo, coincidiendo con F(X) en el intervalo (0; yo) en puntos de continuidad.
La serie de Fourier para una función dada en un intervalo dado tiene la propiedad de unicidad, es decir, si la expansión se obtiene de alguna otra forma que no sea mediante fórmulas, por ejemplo, seleccionando coeficientes, entonces estos coeficientes coinciden con los calculados a partir de las fórmulas. .
Ejemplo No. 1. Ampliar función f(X)=1:
a) en una serie completa de Fourier en el intervalo(-π ;π);
b) en una serie a lo largo de los senos de múltiples arcos en el intervalo(0;π); trazar la serie de Fourier resultante
Solución:
a) La expansión en serie de Fourier en el intervalo (-π;π) tiene la forma: 
,
y todos los coeficientes bn=0, porque esta función es par; De este modo,
Obviamente, la igualdad quedará satisfecha si aceptamos
A 0 =2, A 1 =A 2 =A 3 =…=0
Debido a la propiedad de unicidad, estos son los coeficientes requeridos. Así, la descomposición requerida: 
o simplemente 1=1.
En este caso, cuando una serie coincide idénticamente con su función, la gráfica de la serie de Fourier coincide con la gráfica de la función en toda la recta numérica.
b) La expansión en el intervalo (0;π) en términos de los senos de múltiples arcos tiene la forma:
Obviamente es imposible seleccionar los coeficientes de manera que la igualdad se cumpla de manera idéntica. Usemos la fórmula para calcular los coeficientes:
Así, incluso por norte (norte=2k) tenemos bn=0, para impar ( norte=2k-1) - 
Finalmente, 
.
Tracemos la serie de Fourier resultante usando sus propiedades (ver arriba).
En primer lugar, construimos una gráfica de esta función en un intervalo dado. A continuación, aprovechando la imparidad de la suma de la serie, continuamos la gráfica simétricamente al origen: 
Seguimos de forma periódica a lo largo de toda la recta numérica: 
Y finalmente, en los puntos de ruptura completamos los valores promedio (entre los límites derecho e izquierdo): 
Ejemplo No. 2. Expandir una función 
en el intervalo (0;6) a lo largo de los senos de múltiples arcos.
Solución: La expansión requerida tiene la forma:
Dado que tanto el lado izquierdo como el derecho de la igualdad contienen solo funciones pecado a partir de diferentes argumentos, debe verificar si, para cualquier valor de n (¡natural!), los argumentos de los senos a la izquierda y partes correctas igualdad:
o , de donde n =18. Esto significa que dicho término está contenido en el lado derecho y su coeficiente debe coincidir con el coeficiente del lado izquierdo: b 18 =1;
o , de donde n =4. Medio, b 4 =-5.
Así, seleccionando los coeficientes fue posible obtener la expansión deseada:
Presupuesto del estado federal institución educativa educación más alta
"UNIVERSIDAD ESTATAL DEL VOLGA
TELECOMUNICACIONES E INFORMÁTICA"
Departamento de Matemáticas Superiores
O.V.STAROZHILOVA
CAPÍTULOS ESPECIALES DE MATEMÁTICAS
protocolo No. 45, de fecha 10 de marzo de 2017
Starozhilova, O.V.
C Capítulos especiales de matemáticas.: libro de texto //Starozhilova O.V.. – Samara: PGUTI, 2017. –221 p.
Tutorial toca ramas especiales de las matemáticas: lógica matemática y teoría de autómatas, álgebra proposicional, cálculo proposicional, elementos de la teoría de algoritmos, análisis de regresión, métodos de optimización.
Para estudiantes universitarios y de maestría que estudian en la dirección 09/03/02 " Sistemas y tecnologías de la información.", que quieran estudiar capítulos especiales de matemáticas por su cuenta.
Cada apartado finaliza con preguntas de control que ayudarán a comprobar el dominio teórico del curso, contiene una gran cantidad de tareas para decisión independiente y respuestas para comprobar.
El manual contiene un complejo de laboratorio y una serie de problemas de ingeniería con énfasis en la implementación de software de métodos matemáticos computacionales.
Starozhilova O.V., 2017
Capítulo 1 Análisis Armónico 6
1.1 Problema de cuerdas sonoras 7
1.2 Sistemas ortogonales de funciones 8
1.3 Series de Fourier para el sistema trigonométrico de funciones 10
1.4 Condiciones suficientes expansión de una función en una serie de Fourier 13
1.5 Desarrollo en serie de Fourier de una función no periódica 17
1.6 Series de Fourier para funciones pares e impares 18
1.7 Series de Fourier para funciones de cualquier periodo 21
1.8 Integral de Fourier 27
1.9 Integral de Fourier para funciones pares e impares 29
1.10 forma compleja Integral de Fourier 30
1.11 Transformada de Fourier 32
Capítulo 2 Lógica matemática y IV 33
2.1 Etapas del desarrollo lógico 34
2.2 Lógica proposicional 38
2.3 Conectivos lógicos 40
2.4Operaciones lógicas 41
2.5 Alfabeto de cálculo proposicional 42
2.6 Fórmulas Tautología 42
2.7 Leyes de la lógica proposicional 44
2.8 Teorías formales. Incubabilidad. Interpretación 46
2.9 Método axiomático 47
2.10 Sistema de axiomas del cálculo proposicional (PS) 52
2.11 Reglas de conclusión 53
2.12 Reglas de inferencia derivadas 56
2.13 Construir una conclusión en lógica proposicional 62
2.14 Relación entre álgebra y cálculo proposicional 66
Capítulo 3 Problemas de análisis de regresión 70
3.1 Método mínimos cuadrados 74
3.2 Análisis de regresión lineal 76
3.3 Estimación del modelo de regresión 79
3.4 Problemas al aplicar el método de regresión lineal 83
3.5 Requisitos previos del modelo estadístico LR 85
3.6 Problemas del análisis de regresión 86
3.7 Normal multivariada Modelo de regresión 90
3.8 Variación de la variable dependiente 92
Preguntas del examen 94
Capítulo 4 Formulación general y tipos de problemas de toma de decisiones 95
4.1 Formulación matemática del problema de optimización 97
4.2 TF mínimo local y global 99
4.3 Métodos optimización incondicional 102
4.4 Método de descenso por coordenadas 102
4.5 Método Rosenbrock 105
4.6 Método de configuración 105
4.7 Métodos de búsqueda aleatoria 108
4.8 Método de Newton 112
Capítulo 5 Transformada de Fourier 114
5.1 Aproximación de la función de Fourier 114
5.2 Transformada de Fourier 117
5.3 Transformada rápida de Fourier 120
COMPLEJO DE LABORATORIO 123
Análisis armónico y espectral 123
Tema 1. “Lógica proposicional” 131
Variantes de trabajos individuales para el tema LP 133.
Tema 2. Regresión lineal por pares 140
Trabajo de laboratorio № 1 141
Cálculo de coeficientes de la ecuación LR 141.
Trabajo de laboratorio No. 2 144
Calcular el coeficiente de correlación muestral 144
Trabajo de laboratorio No. 3 145
Cálculo de estimaciones de varianzas de LR 145 emparejado.
Trabajo de laboratorio No. 4 147.
Funciones de Excel para coeficientes LR emparejados 147
Trabajo de laboratorio No. 5 149
Construcción de una estimación de intervalo para la función LR pareada 149
Trabajo de laboratorio No. 6 151
Comprobar la importancia de la ecuación LR utilizando el criterio de Fisher 151
Tema 3 Regresión no lineal por pares 153
Trabajo de laboratorio No. 7 153
Construyendo una regresión no lineal usando 153
Agregar comandos de línea de tendencia 153
Trabajo de laboratorio No. 8 158
Seleccionar la mejor regresión no lineal 158
Tema 4. Lineal regresión múltiple 161
Trabajo de laboratorio No. 9 162
Cálculo de coeficientes LMR 162.
Trabajo de laboratorio No. 10 166
Pruebas de significancia en modo Regresión 166
Tema 5. Regresión múltiple no lineal 175
Trabajo de laboratorio No. 11 175
Cálculo de la función Cobb-Douglas 175
Prueba № 1 179
Regresión emparejada 179
Prueba nº 2 181
Plural regresión lineal 181
Métodos numéricos para buscar un extremo incondicional 185
Análisis gráfico de la función 185.
Problema de búsqueda unidimensional 187
Algoritmo de Svenn 190
Método de fuerza bruta 193
Método de búsqueda bit a bit 195
Método de dicotomía. 198
método fibonacci 201
Método de la proporción áurea 205
Método del punto medio 210
El método de Newton 214
Literatura 218
Capítulo 1 Análisis Armónico
DefiniciónAnálisis armónico- Rama de las matemáticas asociada a la descomposición de vibraciones en vibraciones armónicas.
Al estudiar fenómenos periódicos (es decir, que se repiten en el tiempo), consideramos funciones periódicas.
Por ejemplo, una oscilación armónica se describe mediante una función periódica del tiempo. t:
Ø Definiciónfunción periódica- una función cuyo valor no cambia cuando se llama a un cierto número distinto de cero período funciones.
Dado que la suma y la diferencia de dos períodos es nuevamente un período y, por lo tanto, cualquier múltiplo de un período también es un período, entonces toda función periódica tiene un número infinito de períodos.
Si una función periódica tiene un período real, es continua y diferente de una constante, entonces tiene el período positivo más pequeño t; cualquier otro periodo real de la misma función tendrá la forma kt, Dónde k =±1, ±2,....
La suma, producto y cociente de funciones periódicas con el mismo período son funciones periódicas con el mismo período.
Las funciones periódicas juegan un papel extremadamente importante en la teoría de las oscilaciones y en la física matemática en general. En el curso del análisis matemático, nos familiarizamos con el concepto de serie funcional, trabajamos con su importante caso especial: serie de potencias. Consideremos otro muy importante (incluso para aplicaciones físicas) caso especial series funcionales - series trigonométricas.
Ø Definición Rango funcional – serie de la forma
donde están las funciones que dependen de una variable o de varias variables.
Para cada valor fijo, la serie funcional se convierte en una serie numérica.
que pueden converger o divergir.
Ø Definición Punto de convergencia de series funcionales- el punto en el que converge la serie funcional.
Ø Definición El conjunto de todos los puntos de convergencia se llama región de convergencia de la serie.
Es posible esta función representar en forma de una serie trigonométrica, es decir ¿Es posible encontrar los coeficientes? un Y bn para que haya igualdad para todos
La suma de la serie es obviamente una función periódica. Esto significa que sólo las funciones periódicas se pueden expandir a una serie trigonométrica. F.
Además, está claro que si dos funciones periódicas coinciden en un intervalo cuya longitud es igual al período, entonces coinciden en todas partes. Por tanto, basta con comprobar un determinado intervalo de longitud, por ejemplo, .
1.1 Problema de cuerdas sonoras
El estudio de las series trigonométricas surgió del problema de las cuerdas sonoras planteado en el siglo XVIII.
Dada una función, ¿es posible encontrar una serie trigonométrica que converja y tenga como suma la función? Es necesario imponerle restricciones para que se pueda buscar una serie trigonométrica que converja a ella.
Una tarea similar fue para serie de potencias, si tiene solución, entonces dicha serie es una serie de Taylor.
1.2 Sistemas ortogonales de funciones
El estudio sistemático de los sistemas ortogonales de funciones se inició en relación con el método de Fourier para resolver problemas de valores en la frontera de ecuaciones de física matemática. Uno de los principales problemas en la teoría de los sistemas ortogonales de funciones es el problema de descomponer una función. F(X) en una serie de la forma , donde es un sistema ortogonal de funciones.
Ø Definición Las funciones se llaman ortogonal en , si se cumple:
q Ejemplo , 
- las funciones son ortogonales a , porque 
q Ejemplo on es ortogonal a cualquier función definida en.
Ø Definición Un sistema infinito de funciones se llama ortogonal en si
q Ejemplo Un sistema infinito de funciones no forma un sistema ortogonal de funciones.
q Ejemplo -sistema de funciones trigonométricas forma un sistema de funciones ortogonales a él.
, 
, 
.
Ø Definición Sea un sistema arbitrario de funciones ortogonal a . Fila
donde están los coeficientes numéricos arbitrarios, llamados uno al lado del otro según un sistema ortogonal de funciones.
Ø Definición Series según el sistema trigonométrico de funciones.
llamado series trigonométricas.
ü Comentario Si es la suma de una serie trigonométrica que converge en cada punto, entonces es periódica, ya que , son funciones periódicas con periodo, entonces en la igualdad 
nada cambiará, por lo tanto periódico.
ü Comentario Si se da en el segmento, pero no , entonces desplazando el origen de coordenadas se puede reducir al caso estudiado.
ü Comentario Si una función periódica con periodo no lo es, entonces se expande a una serie trigonométrica.
q Teorema Si una serie numérica converge, entonces la serie trigonométrica
converge absoluta y uniformemente a lo largo de todo el eje.
Prueba
Por eso,
serie: mayoriza una serie trigonométrica dada y, según la prueba de Weierstrass, converge uniformemente.
La convergencia absoluta es obvia.
1.3 Series de Fourier para el sistema trigonométrico de funciones
Jean-Baptiste Joseph Fourier 1768 – 1830 – matemático francés.
Para calcular los coeficientes de la serie de Fourier, calculamos las integrales.
, 
, 
, 
,
q Teorema Si hay igualdad para todos
y la serie trigonométrica converge uniformemente en todo el eje, entonces se determinan los coeficientes de esta serie
, 
,
Prueba
La serie converge uniformemente en toda la recta numérica, sus términos son funciones continuas, luego su suma también es continua y la integración término por término de la serie es posible dentro
Cada integral es igual a cero, porque el sistema trigonométrico de funciones es ortogonal a , y luego
Para demostrarlo, multiplica ambos lados por
Esto no alterará la convergencia uniforme de la serie.
Debido a la convergencia uniforme de la serie.
y esto significa convergencia uniforme de la serie.
Integrando en , tenemos
Debido a la ortogonalidad del sistema trigonométrico de funciones en
, 
, y de 
la integral en ,
, eso, etc
recordemos eso
La validez de estas igualdades se deriva de la aplicación de fórmulas trigonométricas al integrando.
La fórmula para se prueba de manera similar.
ü Comentario El teorema sigue siendo válido en cualquier intervalo y los límites de integración se reemplazan por y respectivamente.
Ø Definición Serie trigonométrica
,
cuyos coeficientes están determinados por las fórmulas
, ,
,
llamado cerca de Fourier para la función, y los coeficientes se llaman coeficientes de Fourier.
Si la serie de Fourier de la función f(x) converge en todos sus puntos de continuidad, entonces decimos que la función f(x) se expande a una serie de Fourier.
ü Comentario No todas las series trigonométricas son series de Fourier, incluso si convergen en toda la recta numérica.
La suma de una serie no uniformemente convergente puede ser discontinua y no integrable, por lo que es imposible determinar los coeficientes de Fourier.
ü Comentario La serie de Fourier es un caso especial de serie funcional.
1.4 Condiciones suficientes para el desarrollo de una función en una serie de Fourier
Ø Definición La función se llama monótono por partes en el segmento, si este segmento se puede dividir por un número finito de puntos x 1 , x 2 , ..., x n-1 en intervalos ( a,x1), (x1,x2), ..., (xn-1,b) de modo que en cada uno de los intervalos la función es monótona, es decir, no aumenta o no disminuye.
ü Comentario De la definición se deduce que si una función es monótona por partes y está acotada a [ a,b], entonces sólo tiene discontinuidades del primer tipo.
Ø Definición La función se llama suave a trozos, si en cada intervalo finito él y su derivada tienen como máximo un número finito de puntos de discontinuidad de primer tipo.
q Teorema (condición de Dirichlet) condición suficiente para la descomponibilidad de una función en una serie de Fourier): Si una función periódica con un período satisface una de las condiciones:
entonces la serie de Fourier construida para esta función converge en todos los puntos
y converge al número 
en cada punto de su discontinuidad.
La suma de la serie resultante es igual al valor de la función en los puntos de continuidad de la función.
Funciones, descomponiéndolas en componentes. Las corrientes y voltajes alternos, los desplazamientos, la velocidad y aceleración de los mecanismos de manivela y las ondas acústicas son ejemplos prácticos típicos del uso de funciones periódicas en los cálculos de ingeniería.
La expansión de la serie de Fourier se basa en el supuesto de que todas las funciones de importancia práctica en el intervalo -π ≤x≤ π pueden expresarse en forma de series trigonométricas convergentes (una serie se considera convergente si la secuencia de sumas parciales compuesta por sus términos converge):
Notación estándar (=ordinaria) mediante la suma de senx y cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
donde a o, a 1,a 2,...,b 1,b 2,.. son constantes reales, es decir
Donde, para el rango de -π a π, los coeficientes de la serie de Fourier se calculan mediante las fórmulas:
Los coeficientes a o , a n y b n se llaman coeficientes de Fourier, y si se pueden encontrar, entonces la serie (1) se llama junto a Fourier, correspondiente a la función f(x). Para la serie (1), el término (a 1 cosx+b 1 senx) se llama primero o armónico fundamental,
Otra forma de escribir una serie es usar la relación acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Donde a o es una constante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 son las amplitudes de las distintas componentes, y es igual a a n =arctg a n /b n.
Para la serie (1), el término (a 1 cosx+b 1 sinx) o c 1 sin(x+α 1) se llama primero o armónico fundamental,(a 2 cos2x+b 2 sin2x) o c 2 sin(2x+α 2) se llama segundo armónico etcétera.
Para representar con precisión una señal compleja normalmente se requiere un número infinito de términos. Sin embargo, en muchos problemas prácticos es suficiente considerar sólo los primeros términos.
Serie de Fourier de funciones no periódicas con período 2π.
Ampliación de funciones no periódicas a series de Fourier.
Si la función f(x) no es periódica, significa que no se puede expandir a una serie de Fourier para todos los valores de x. Sin embargo, es posible definir una serie de Fourier que represente una función en cualquier rango de ancho 2π.
Dada una función no periódica, se puede construir una nueva función seleccionando valores de f(x) dentro de un cierto rango y repitiéndolos fuera de ese rango en intervalos de 2π. Dado que la nueva función es periódica con período 2π, se puede expandir a una serie de Fourier para todos los valores de x. Por ejemplo, la función f(x)=x no es periódica. Sin embargo, si es necesario expandirlo a una serie de Fourier en el intervalo de o a 2π, entonces fuera de este intervalo se construye una función periódica con un período de 2π (como se muestra en la figura siguiente).
Para funciones no periódicas como f(x)=x, la suma de la serie de Fourier es igual al valor de f(x) en todos los puntos en un rango dado, pero no es igual a f(x) para los puntos fuera del rango. Para encontrar la serie de Fourier de una función no periódica en el rango 2π, se utiliza la misma fórmula de los coeficientes de Fourier.
Funciones pares e impares.
Dicen que la función y=f(x) incluso, si f(-x)=f(x) para todos los valores de x. Las gráficas de funciones pares siempre son simétricas con respecto al eje y (es decir, son imágenes especulares). Dos ejemplos de funciones pares: y=x2 e y=cosx.
Dicen que la función y=f(x) extraño, si f(-x)=-f(x) para todos los valores de x. Las gráficas de funciones impares siempre son simétricas con respecto al origen.
Muchas funciones no son ni pares ni impares.
Desarrollo en series de Fourier en cosenos.
La serie de Fourier de una función periódica par f(x) con período 2π contiene sólo términos cosenos (es decir, no hay términos senos) y puede incluir un término constante. Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
La serie de Fourier de una función periódica impar f(x) con periodo 2π contiene sólo términos con senos (es decir, no contiene términos con cosenos).
Por eso,
¿Dónde están los coeficientes de la serie de Fourier?
Serie de Fourier en medio ciclo.
Si una función se define para un rango, digamos de 0 a π, y no sólo de 0 a 2π, se puede expandir en una serie sólo en senos o sólo en cosenos. La serie de Fourier resultante se llama cerca de Fourier a medio ciclo.
Si quieres obtener la descomposición. Fourier de medio ciclo por cosenos funciones f(x) en el rango de 0 a π, entonces es necesario construir una función periódica par. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función par es simétrica con respecto al eje f(x), trazamos la línea AB, como se muestra en la figura. abajo. Si asumimos que fuera del intervalo considerado la forma triangular resultante es periódica con un período de 2π, entonces el gráfico final se ve así: en la Fig. abajo. Como necesitamos obtener el desarrollo de Fourier en cosenos, como antes, calculamos los coeficientes de Fourier a o y a n
Si desea obtener funciones f(x) en el rango de 0 a π, entonces necesita construir una función periódica impar. En la Fig. A continuación se muestra la función f(x)=x, construida en el intervalo de x=0 a x=π. Como la función impar es simétrica con respecto al origen, construimos la recta CD, como se muestra en la figura. Si asumimos que fuera del intervalo considerado la señal en diente de sierra resultante es periódica con un período de 2π, entonces la gráfica final tiene la forma que se muestra en la Fig. Como necesitamos obtener la expansión de Fourier del semiciclo en términos de senos, como antes, calculamos el coeficiente de Fourier. b
Serie de Fourier para un intervalo arbitrario.
Expansión de una función periódica con período L.
La función periódica f(x) se repite cuando x aumenta en L, es decir f(x+L)=f(x). La transición de las funciones previamente consideradas con un período de 2π a funciones con un período de L es bastante simple, ya que se puede realizar mediante un cambio de variable.
Para encontrar la serie de Fourier de la función f(x) en el rango -L/2≤x≤L/2, introducimos una nueva variable u para que la función f(x) tenga un período de 2π con respecto a u. Si u=2πx/L, entonces x=-L/2 para u=-π y x=L/2 para u=π. También dejemos f(x)=f(Lu/2π)=F(u). La serie de Fourier F(u) tiene la forma
¿Dónde están los coeficientes de la serie de Fourier?
Sin embargo, lo más frecuente es que la fórmula anterior resulte en una dependencia de x. Dado que u=2πx/L, significa du=(2π/L)dx, y los límites de integración son de -L/2 a L/2 en lugar de - π a π. En consecuencia, la serie de Fourier para la dependencia de x tiene la forma
donde en el rango de -L/2 a L/2 están los coeficientes de la serie de Fourier,
(Los límites de integración se pueden reemplazar por cualquier intervalo de longitud L, por ejemplo, de 0 a L)
Serie de Fourier en medio ciclo para funciones especificadas en el intervalo L≠2π.
Para la sustitución u=πх/L, el intervalo de x=0 a x=L corresponde al intervalo de u=0 a u=π. En consecuencia, la función se puede expandir en una serie solo en cosenos o solo en senos, es decir V Serie de Fourier en medio ciclo..
La expansión del coseno en el rango de 0 a L tiene la forma
