Mencari turunan dari fungsi trigonometri perlu digunakan tabel turunan, yaitu turunan 6-13.
Ketika Anda menemukannya turunan prima fungsi trigonometri Untuk menghindari kesalahan umum, sebaiknya perhatikan hal-hal berikut ini:
- dalam ekspresi fungsi, salah satu sukunya adalah sering sinus, kosinus atau fungsi trigonometri lainnya bukan dari argumen fungsinya, tetapi dari bilangan (konstanta), oleh karena itu turunan suku tersebut sama dengan nol;
- hampir selalu Anda perlu menyederhanakan ekspresi yang diperoleh sebagai hasil diferensiasi, dan untuk ini Anda perlu menggunakan pengetahuan tentang operasi dengan pecahan dengan percaya diri;
- Untuk menyederhanakan suatu ekspresi, Anda hampir selalu perlu mengetahui identitas trigonometri, misalnya rumusnya sudut ganda dan rumus kesatuan sebagai jumlah kuadrat sinus dan kosinus.
Contoh 1. Temukan turunan suatu fungsi
Larutan. Katakanlah dengan turunan kosinus semuanya jelas, kata banyak orang yang mulai mempelajari turunan. Bagaimana dengan turunan dari sinus dua belas dibagi pi? Jawaban: anggap sama dengan nol! Di sini sinus (bagaimanapun juga, suatu fungsi!) adalah jebakan, karena argumennya bukanlah variabel X atau variabel lain, melainkan hanya angka. Artinya, sinus dari bilangan ini juga merupakan bilangan. Dan turunan suatu bilangan (konstanta), seperti yang kita ketahui dari tabel turunan, sama dengan nol. Jadi, kita hanya menyisakan sinus minus dari X dan mencari turunannya, tanpa melupakan tandanya:
![]() .
.
Contoh 2. Temukan turunan suatu fungsi
![]() .
.
Larutan. Kasus suku kedua sama dengan suku pertama pada contoh sebelumnya. Artinya, itu adalah bilangan, dan turunan dari bilangan tersebut adalah nol. Kami menemukan turunan suku kedua sebagai turunan dari hasil bagi:
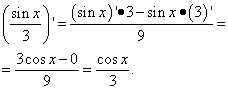
Contoh 3. Temukan turunan suatu fungsi
Larutan. Ini masalah lain: di sini pada suku pertama tidak ada arcsinus atau fungsi trigonometri lainnya, tetapi ada x, yang artinya merupakan fungsi dari x. Oleh karena itu, kami membedakannya sebagai suku dalam jumlah fungsi:

Di sini diperlukan keterampilan dalam mengoperasikan pecahan, yaitu menghilangkan struktur pecahan bertingkat tiga.
Contoh 4. Temukan turunan suatu fungsi
![]() .
.
Larutan. Di sini huruf "phi" memainkan peran yang sama dengan "x" dalam kasus sebelumnya (dan di sebagian besar kasus lainnya, tetapi tidak semua) - variabel independen. Oleh karena itu, ketika kita mencari turunan suatu produk suatu fungsi, kita tidak akan terburu-buru menyatakan turunan dari akar “phi” sama dengan nol. Jadi:
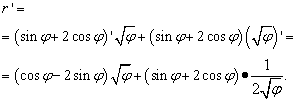
Namun solusinya tidak berakhir di situ. Karena suku-suku serupa dikumpulkan dalam dua tanda kurung, kita masih perlu mengubah (menyederhanakan) ekspresi tersebut. Oleh karena itu, kita mengalikan tanda kurung dengan faktor di belakangnya, lalu kita membawa suku-suku tersebut ke penyebut yang sama dan melakukan transformasi dasar lainnya:

Contoh 5. Temukan turunan suatu fungsi
Larutan. Dalam contoh ini, kita perlu mengetahui fakta bahwa ada fungsi trigonometri - garis potong - dan rumusnya melalui kosinus. Mari kita bedakan:

Contoh 6. Temukan turunan suatu fungsi
![]() .
.
Larutan. Pada contoh ini kita akan diminta untuk mengingat rumus sudut ganda dari sekolah. Tapi pertama-tama mari kita bedakan:

![]() ,
,
(inilah rumus sudut rangkap dua)
Disajikan turunan fungsi trigonometri invers dan turunan rumusnya. Ekspresi untuk turunan orde tinggi juga diberikan. Tautan ke halaman dengan penjelasan lebih rinci tentang derivasi rumus.
Pertama, kita turunkan rumus turunan arcsinus. Membiarkan
kamu= busur x.
Karena arcsinus adalah kebalikan dari fungsi sinus, maka
.
Di sini y adalah fungsi dari x. Diferensialkan terhadap variabel x:
.
Kami melamar:
.
Jadi kami menemukan:
.
Karena, kalau begitu. Kemudian
.
Dan rumus sebelumnya berbentuk:
. Dari sini
.
Dengan cara yang persis seperti ini, Anda bisa mendapatkan rumus turunan dari arc cosinus. Namun, lebih mudah menggunakan rumus yang berkaitan dengan fungsi trigonometri terbalik:
.
Kemudian
.
Penjelasan lebih rinci disajikan pada halaman “Derivasi turunan arcsinus dan arccosine”. Itu diberikan di sana derivasi turunan dengan dua cara- dibahas di atas dan menurut rumus turunan fungsi invers.
Penurunan turunan dari arctangent dan arccotangent
Dengan cara yang sama kita akan mencari turunan dari arctangent dan arccotangent.
Membiarkan
kamu= arctan x.
Arctangent adalah kebalikan dari fungsi tangen:
.
Diferensialkan terhadap variabel x:
.
Kami menerapkan rumus turunan fungsi kompleks:
.
Jadi kami menemukan:
.
Turunan dari kotangen busur:
.
Turunan arcsin
Membiarkan
.
Kami telah menemukan turunan orde pertama dari arcsinus:
.
Dengan melakukan diferensiasi, kita mencari turunan orde kedua:
;
.
Bisa juga ditulis dalam bentuk berikut:
.
Dari sini kita dapatkan persamaan diferensial, yang dipenuhi oleh turunan arcsinus orde pertama dan kedua:
.
Dengan mendiferensiasikan persamaan ini, kita dapat mencari turunan orde tinggi.
Turunan dari arcsinus orde ke-n
Turunan dari arcsinus orde ke-n mempunyai bentuk sebagai berikut:
,
di mana adalah polinomial derajat. Itu ditentukan oleh rumus:
;
.
Di Sini .
Polinomial memenuhi persamaan diferensial:
.
Turunan dari arccosine orde ke-n
Turunan busur cosinus diperoleh dari turunan busur sinus dengan menggunakan rumus trigonometri:
.
Oleh karena itu, turunan dari fungsi-fungsi ini hanya berbeda tandanya:
.
Turunan dari arctangent
Membiarkan . Kami menemukan turunan dari kotangen busur orde pertama:
.
Mari kita pecahkan pecahan menjadi bentuk yang paling sederhana:
.
Berikut adalah satuan imajinernya, .
Kami membedakan satu kali dan membawa pecahan ke penyebut yang sama:
.
Mengganti , kita mendapatkan:
.
Turunan dari arctangen orde ke-n
Jadi, turunan dari garis singgung busur orde ke-n dapat direpresentasikan dalam beberapa cara:
;
.
Turunan dari kotangen busur
Biarkan saja sekarang. Mari kita terapkan rumus yang menghubungkan fungsi trigonometri terbalik:
.
Maka turunan ke-n garis singgung busur hanya berbeda tandanya dengan turunan garis singgung busur:
.
Mengganti , kita menemukan:
.
Referensi:
N.M. Gunter, RO. Kuzmin, Kumpulan Masalah Matematika Tinggi, “Lan”, 2003.
Saat menurunkan rumus pertama tabel, kita akan melanjutkan dari definisi turunan fungsi di suatu titik. Ayo bawa kemana X– bilangan real apa pun, yaitu, X– bilangan apa pun dari domain definisi fungsi. Mari kita tuliskan limit rasio pertambahan fungsi terhadap pertambahan argumen di : ![]()
Perlu dicatat bahwa di bawah tanda batas diperoleh ekspresi yang bukan merupakan ketidakpastian nol dibagi nol, karena pembilangnya tidak mengandung nilai yang sangat kecil, melainkan nol. Dengan kata lain, pertambahan fungsi konstanta selalu nol.
Dengan demikian, turunan dari fungsi konstansama dengan nol di seluruh domain definisi.
Turunan dari fungsi pangkat.
Rumus turunan fungsi daya seperti ![]() , di mana eksponennya P– bilangan real apa pun.
, di mana eksponennya P– bilangan real apa pun.
Mari kita buktikan dulu rumus eksponen naturalnya, yaitu untuk p = 1, 2, 3, …
Kami akan menggunakan definisi turunan. Mari kita tuliskan limit rasio pertambahan fungsi pangkat dengan pertambahan argumen: 
Untuk menyederhanakan ekspresi pembilangnya, kita beralih ke rumus binomial Newton: 
Karena itu, 
Hal ini membuktikan rumus turunan fungsi pangkat eksponen natural.
Turunan dari fungsi eksponensial.
Kami menyajikan turunan rumus turunan berdasarkan definisi:
Kita telah sampai pada ketidakpastian. Untuk memperluasnya, kami memperkenalkan variabel baru, dan pada . Kemudian . Pada transisi terakhir, kami menggunakan rumus untuk beralih ke basis logaritma baru.
Mari kita substitusikan ke dalam limit aslinya: 
Jika kita mengingat limit luar biasa kedua, kita sampai pada rumus turunan fungsi eksponensial: 
Turunan dari fungsi logaritma.
Mari kita buktikan rumus turunan fungsi logaritma untuk semua X dari domain definisi dan semua nilai basis yang valid A logaritma Berdasarkan definisi turunan kita mempunyai: 
Seperti yang Anda perhatikan, selama pembuktian, transformasi dilakukan menggunakan sifat-sifat logaritma. Persamaan  benar karena batas luar biasa kedua.
benar karena batas luar biasa kedua.
Turunan dari fungsi trigonometri.
Untuk mendapatkan rumus turunan fungsi trigonometri, kita harus mengingat beberapa rumus trigonometri, serta limit pertama yang luar biasa.
Berdasarkan definisi turunan fungsi sinus yang kita miliki ![]() .
.
Mari kita gunakan rumus selisih sinus: 
Masih beralih ke batas luar biasa pertama: 
Jadi, turunan dari fungsi tersebut dosa x Ada karena x.
Rumus turunan kosinus dibuktikan dengan cara yang persis sama. 
Oleh karena itu, turunan dari fungsi tersebut karena x Ada –dosa x.
Kita akan menurunkan rumus tabel turunan tangen dan kotangen menggunakan aturan diferensiasi yang telah terbukti (turunan pecahan). 
Turunan dari fungsi hiperbolik.
Aturan diferensiasi dan rumus turunan fungsi eksponensial dari tabel turunan memungkinkan kita memperoleh rumus turunan sinus hiperbolik, kosinus, tangen, dan kotangen. 
Turunan dari fungsi invers.
Untuk menghindari kebingungan saat presentasi, mari kita nyatakan dalam subskrip argumen fungsi yang digunakan untuk melakukan diferensiasi, yaitu turunan dari fungsi tersebut. f(x) Oleh X.
Sekarang mari kita rumuskan aturan untuk mencari turunan suatu fungsi invers.
Biarkan fungsinya kamu = f(x) Dan x = g(kamu) saling berbanding terbalik, ditentukan pada interval dan masing-masing. Jika pada suatu titik terdapat turunan berhingga dari fungsi tersebut f(x), maka pada titik tersebut terdapat turunan berhingga dari fungsi inversnya g(kamu), Dan ![]() . Di postingan lain
. Di postingan lain ![]() .
.
Aturan ini dapat dirumuskan ulang untuk siapa pun X dari interval , maka kita peroleh  .
.
Mari kita periksa validitas rumus ini.
Mari kita cari fungsi invers logaritma natural ![]() (Di Sini kamu adalah fungsi, dan X- argumen). Setelah menyelesaikan persamaan ini untuk X, kita dapatkan (di sini X adalah fungsi, dan kamu– argumennya). Itu adalah,
(Di Sini kamu adalah fungsi, dan X- argumen). Setelah menyelesaikan persamaan ini untuk X, kita dapatkan (di sini X adalah fungsi, dan kamu– argumennya). Itu adalah, ![]() dan fungsi yang saling invers.
dan fungsi yang saling invers.
Dari tabel turunan kita melihatnya ![]() Dan
Dan ![]() .
.
Mari kita pastikan bahwa rumus untuk mencari turunan fungsi invers memberikan hasil yang sama: 
Dari mata kuliah geometri dan matematika, anak sekolah dibiasakan dengan kenyataan bahwa konsep turunan disampaikan kepada mereka melalui luas bangun, selisih, limit fungsi, serta limit. Mari kita coba melihat konsep turunan dari sudut yang berbeda, dan menentukan bagaimana turunan dan fungsi trigonometri dapat dihubungkan.
Jadi, mari kita perhatikan beberapa kurva sembarang yang dijelaskan oleh fungsi abstrak y = f(x).
Bayangkan jadwalnya adalah peta jalur wisata. Pertambahan ∆x (delta x) pada gambar adalah jarak lintasan tertentu, dan ∆y adalah perubahan ketinggian lintasan di atas permukaan laut.
Kemudian ternyata rasio ∆x/∆y akan mencirikan kompleksitas rute pada setiap ruas rute. Setelah mempelajari nilai ini, Anda dapat dengan yakin mengatakan apakah pendakian/penurunannya curam, apakah Anda memerlukan peralatan pendakian, dan apakah wisatawan memerlukan peralatan tertentu. Latihan fisik. Namun indikator ini hanya berlaku untuk satu interval kecil ∆x.
Jika penyelenggara perjalanan mengambil nilai titik awal dan akhir lintasan, yaitu x sama dengan panjang lintasan, maka ia tidak akan dapat memperoleh data obyektif mengenai tingkat kesulitannya. dari perjalanan. Oleh karena itu, perlu dibuat grafik lain yang dapat mencirikan kecepatan dan “kualitas” perubahan lintasan, dengan kata lain menentukan rasio ∆x/∆y untuk setiap “meter” lintasan.
Grafik ini akan menjadi turunan visual untuk jalur tertentu dan secara objektif akan menggambarkan perubahannya pada setiap interval yang diinginkan. Sangat mudah untuk memverifikasi ini; nilai ∆x/∆y tidak lebih dari diferensial yang diambil untuk nilai tertentu dari x dan y. Mari kita terapkan diferensiasi bukan pada koordinat tertentu, tetapi pada fungsi secara keseluruhan:

Fungsi turunan dan trigonometri
Fungsi trigonometri terkait erat dengan turunan. Hal ini dapat dipahami dari gambar berikut. Gambar sumbu koordinat menunjukkan fungsi Y = f(x) - kurva berwarna biru.
K (x0; f (x0)) adalah titik sembarang, x0 + ∆x adalah pertambahan sepanjang sumbu OX, dan f (x0 + ∆x) adalah pertambahan sepanjang sumbu OY pada titik tertentu L.

Mari kita menggambar garis lurus melalui titik K dan L dan membangunnya segitiga siku-siku KLN. Jika secara mental segmen LN dipindahkan sepanjang grafik Y = f (x), maka titik L dan N akan cenderung ke nilai K (x0; f (x0)). Sebut saja titik ini sebagai awal bersyarat dari grafik - batas; jika fungsinya tidak terbatas, setidaknya pada salah satu interval, kecenderungan ini juga akan menjadi tidak terbatas, dan nilai batasnya mendekati 0.
Sifat kecenderungan ini dapat digambarkan dengan garis singgung titik terpilih y = kx + b atau dengan grafik turunan dari fungsi awal dy - garis lurus berwarna hijau.
Tapi di manakah trigonometri di sini?! Semuanya sangat sederhana, perhatikan segitiga siku-siku KLN. Nilai diferensial suatu titik K adalah garis singgung sudut α atau ∠K:

Dengan demikian, kita dapat mendeskripsikan makna geometri turunan dan hubungannya dengan fungsi trigonometri.
Rumus turunan fungsi trigonometri
Transformasi sinus, cosinus, tangen, dan kotangen dalam menentukan turunannya harus dihafal.

Dua rumus terakhir tidak error, intinya ada perbedaan antara mendefinisikan turunan argumen sederhana dan fungsi dalam kapasitas yang sama.
Mari kita lihat tabel perbandingan rumus turunan sinus, cosinus, tangen dan kotangen:

Rumus juga telah diturunkan untuk turunan arcsinus, arccosine, arctangent, dan arccotangent, meskipun rumus tersebut sangat jarang digunakan:

Perlu dicatat bahwa rumus di atas jelas tidak cukup untuk berhasil menyelesaikan tugas-tugas USE umum, yang akan ditunjukkan saat menyelesaikan contoh spesifik mencari turunan dari ekspresi trigonometri.
Latihan: Kita perlu mencari turunan dari fungsi tersebut dan mencari nilainya untuk π/4:

Larutan: Untuk mencari y’ perlu diingat kembali rumus dasar untuk mengubah fungsi asli menjadi turunan yaitu.
Subjek:"Turunan fungsi trigonometri".
Jenis pelajaran– pelajaran dalam mengkonsolidasikan pengetahuan.
Bentuk pelajaran– pelajaran terpadu.
Tempat pelajaran dalam sistem pelajaran untuk bagian ini- pelajaran umum.
Sasaran ditetapkan secara komprehensif:
- pendidikan: mengetahui kaidah diferensiasi, mampu menerapkan kaidah penghitungan turunan dalam menyelesaikan persamaan dan pertidaksamaan; meningkatkan mata pelajaran, termasuk komputasi, keterampilan dan kemampuan; Keahlian komputer;
- mengembangkan: pengembangan keterampilan intelektual dan logis serta minat kognitif;
- pendidikan: menumbuhkan kemampuan beradaptasi terhadap kondisi modern pelatihan.
Metode:
- reproduktif dan produktif;
- praktis dan verbal;
- pekerjaan mandiri;
- pembelajaran terprogram, TSO;
- kombinasi frontal, grup dan pekerjaan individu;
- pembelajaran yang dibedakan;
- induktif-deduktif.
Bentuk pengendalian:
- survei lisan,
- kontrol terprogram,
- pekerjaan mandiri,
- tugas individu di komputer,
- peer review menggunakan kartu diagnostik siswa.
SELAMA KELAS
I. Momen organisasi
II. Memperbarui pengetahuan referensi
a) Mengkomunikasikan maksud dan tujuan:
- mengetahui kaidah diferensiasi, mampu menerapkan kaidah penghitungan turunan dalam menyelesaikan masalah, persamaan dan pertidaksamaan;
- meningkatkan mata pelajaran, termasuk komputasi, keterampilan dan kemampuan; Keahlian komputer;
- mengembangkan keterampilan intelektual dan logis serta minat kognitif;
- menumbuhkan kemampuan beradaptasi dengan kondisi pembelajaran modern.
b) Pengulangan materi pendidikan
Aturan penghitungan turunan (pengulangan rumus di komputer dengan suara). Dok.7.
- Apa turunan dari sinus?
- Apa turunan dari cosinus?
- Apa turunan dari garis singgung?
- Apa turunan dari kotangen?
AKU AKU AKU. Pekerjaan lisan
Temukan turunannya. |
|||
Pilihan 1. |
Pilihan 2. |
||
pada = 2X + 5. |
pada = 2X – 5. |
||
pada= 4cos X. |
pada= 3dosa X. |
||
pada= tg X+ctg X. |
pada= tg X-ctg X. |
||
pada= dosa 3 X. |
pada= karena 4 X. |
||
Pilihan jawaban. |
|||
– 4 dosa X |
– 3ko X |
||
1/karena 2 X+ 1/dosa 2 X |
1/karena 2 X–1/dosa 2 X |
1/dosa 2 X–1/karena 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Bertukar buku catatan. Di kartu diagnostik, tandai tugas yang diselesaikan dengan benar dengan tanda +, dan tugas yang diselesaikan salah dengan tanda –.
IV. Menyelesaikan persamaan menggunakan turunan
– Bagaimana cara mencari titik yang turunannya nol?
Untuk mencari titik-titik turunannya fungsi ini sama dengan nol, Anda memerlukan:
– menentukan sifat fungsinya,
– temukan daerahnya definisi fungsi,
– temukan turunan dari fungsi ini,
– selesaikan persamaannya F "(X) = 0,
- Pilih jawaban yang benar.
Tugas 1.
Diberikan: pada
= X-dosa X.
Menemukan: titik yang turunannya nol.
Larutan. Fungsi terdefinisi dan terdiferensiasi pada himpunan semua bilangan real, karena fungsi terdefinisi dan terdiferensiasi pada himpunan semua bilangan real G(X) = X Dan T(X) = – dosa X.
Dengan menggunakan aturan diferensiasi, kita peroleh F
"(X) = (X-dosa X)" = (X)" – (dosa X)" = 1 – cos X.
Jika F "(X) = 0, lalu 1 – cos X = 0.
karena X= 1/; mari kita hilangkan irasionalitas pada penyebutnya, kita dapatkan cos X
= /2.
Menurut rumusnya T= ± arccos A+ 2n, n Z, kita peroleh: X= ± arccos /2 + 2n, n Z.
Menjawab: x = ± /4 + 2n, n Z.
V. Menyelesaikan persamaan menggunakan algoritma
Temukan di titik mana turunannya hilang.
F(X) = dosa X+karena X |
F(X) = dosa 2 X – X |
F(X) = 2X+karena(4 X – ) |
Siswa dapat memilih salah satu dari tiga contoh. Contoh pertama diberi peringkat " 3 ", Kedua - " 4 ", ketiga - " 5 " Penyelesaian dalam buku catatan dilanjutkan dengan saling mengecek. Seorang siswa memutuskan di papan tulis. Jika penyelesaiannya ternyata salah, maka siswa perlu kembali ke algoritma dan mencoba menyelesaikannya lagi.
Kontrol terprogram.
Pilihan 1 |
pilihan 2 |
|||
kamu = 2X 3 |
kamu = 3X 2 |
|||
kamu = 1/4 X 4 + 2X 2 – 7 |
kamu = 1/2 X 4 + 4X + 5 |
|||
kamu = X 3 + 4X 2
– 3X. |
kamu = 2X 3 – 9X 2
+ 12X + 7. |
|||
kamu= dosa 2 X– karena 3 X. |
kamu= karena 2 X– dosa 3 X. |
|||
kamu= tg X–ctg( X + /4). |
kamu=ctg X+tg( X – /4). |
|||
kamu= dosa 2 X. |
kamu= karena 2 X. |
|||
Pilihan jawaban. |
||||
|
| ||||








