നിർവ്വചനം. ഒരു ഫംഗ്ഷൻ f(x) ചില ഇടവേളകളിൽ നിർവചിക്കട്ടെ, ഈ ഇടവേളയിൽ x 0 ഒരു ബിന്ദുവായിരിക്കട്ടെ. എങ്കിൽ, x 0 എന്ന ബിന്ദുവിൽ f(x) തുടർച്ചയായിരിക്കുമെന്ന് പറയപ്പെടുന്നു.
നിർവചനത്തിൽ നിന്ന്, f(x) നിർവചിച്ചിരിക്കുന്ന പോയിന്റുകളുമായി ബന്ധപ്പെട്ട് മാത്രമേ നമുക്ക് തുടർച്ചയെക്കുറിച്ച് സംസാരിക്കാൻ കഴിയൂ (ഒരു ഫംഗ്ഷന്റെ പരിധി നിർവചിക്കുമ്പോൾ, അത്തരമൊരു വ്യവസ്ഥ സജ്ജീകരിച്ചിട്ടില്ല). തുടർച്ചയായ പ്രവർത്തനങ്ങൾക്ക് , അതായത്, f, lim എന്നീ പ്രവർത്തനങ്ങൾ മാറ്റാവുന്നവയാണ്. അതനുസരിച്ച്, ഒരു ഘട്ടത്തിലെ ഒരു ഫംഗ്ഷന്റെ പരിധിയുടെ രണ്ട് നിർവചനങ്ങൾക്ക് തുടർച്ചയുടെ രണ്ട് നിർവചനങ്ങൾ നൽകാം - “ക്രമങ്ങളുടെ ഭാഷയിൽ”, “അസമത്വങ്ങളുടെ ഭാഷയിൽ” (ε-δ ഭാഷയിൽ). ഇത് സ്വയം ചെയ്യാൻ നിർദ്ദേശിക്കുന്നു.
പ്രായോഗിക ഉപയോഗത്തിന്, ഇൻക്രിമെന്റുകളുടെ ഭാഷയിൽ തുടർച്ച നിർവ്വചിക്കുന്നത് ചിലപ്പോൾ കൂടുതൽ സൗകര്യപ്രദമാണ്.
Δx=x-x 0 എന്ന മൂല്യത്തെ ആർഗ്യുമെന്റിന്റെ ഇൻക്രിമെന്റ് എന്നും Δy=f(x)-f(x 0) എന്നത് പോയിന്റ് x 0 ൽ നിന്ന് പോയിന്റ് x ലേക്ക് നീങ്ങുമ്പോൾ ഫംഗ്ഷന്റെ വർദ്ധനവുമാണ്.
നിർവ്വചനം. x 0 പോയിന്റിൽ f(x) നിർവചിക്കട്ടെ. ഈ പോയിന്റിലെ ആർഗ്യുമെന്റിന്റെ അനന്തമായ ഇൻക്രിമെന്റ് ഫംഗ്ഷന്റെ അനന്തമായ ഇൻക്രിമെന്റുമായി പൊരുത്തപ്പെടുന്നെങ്കിൽ, അതായത്, Δx→0-നുള്ള Δy→0 എന്ന ബിന്ദുവിൽ f(x) എന്ന ഫംഗ്ഷനെ തുടർച്ചയായി വിളിക്കുന്നു.

ഉദാഹരണം 1. x ന്റെ ഏത് മൂല്യത്തിനും y=sinx ഫംഗ്ഷൻ തുടർച്ചയായി ഉണ്ടെന്ന് തെളിയിക്കുക.
പരിഹാരം. x 0 ഒരു അനിയന്ത്രിതമായ പോയിന്റ് ആയിരിക്കട്ടെ. ഒരു ഇൻക്രിമെന്റ് Δx കൊടുത്താൽ നമുക്ക് x=x 0 +Δx എന്ന പോയിന്റ് ലഭിക്കും. പിന്നെ . നമുക്ക് ലഭിക്കുന്നു .
നിർവ്വചനം. y=f(x) എന്ന ഫംഗ്‌ഷനെ വലത് (ഇടത്) x 0 പോയിന്റിൽ തുടർച്ചയായി വിളിക്കുന്നു if
.
ഒരു ഇന്റീരിയർ പോയിന്റിൽ തുടർച്ചയായ ഒരു പ്രവർത്തനം വലത്തും ഇടത്തും തുടർച്ചയായിരിക്കും. സംഭാഷണവും ശരിയാണ്: ഒരു ഫംഗ്ഷൻ ഇടത്തും വലത്തും ഒരു ബിന്ദുവിൽ തുടർച്ചയായി ആണെങ്കിൽ, ആ ഘട്ടത്തിൽ അത് തുടർച്ചയായിരിക്കും. എന്നിരുന്നാലും, ഒരു ഫംഗ്‌ഷൻ ഒരു വശത്ത് മാത്രമേ തുടർച്ചയായി നിലനിൽക്കൂ. ഉദാഹരണത്തിന്, വേണ്ടി , , f(1)=1, അതിനാൽ, ഈ ഫംഗ്‌ഷൻ ഇടതുവശത്ത് മാത്രം തുടർച്ചയായിരിക്കും (ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫിനായി, മുകളിലുള്ള ഖണ്ഡിക 5.7.2 കാണുക).
നിർവ്വചനം. ഈ ഇടവേളയുടെ ഓരോ ബിന്ദുവിലും ഒരു ഫംഗ്ഷൻ തുടർച്ചയായി ആണെങ്കിൽ ചില ഇടവേളകളിൽ തുടർച്ചയായി വിളിക്കുന്നു.
പ്രത്യേകിച്ചും, ഇടവേള ഒരു സെഗ്‌മെന്റാണെങ്കിൽ, അതിന്റെ അറ്റത്ത് ഏകപക്ഷീയമായ തുടർച്ച സൂചിപ്പിക്കുന്നു.

തുടർച്ചയായ പ്രവർത്തനങ്ങളുടെ ഗുണവിശേഷതകൾ

1. എല്ലാ എലിമെന്ററി ഫംഗ്ഷനുകളും അവയുടെ നിർവചനത്തിന്റെ ഡൊമെയ്നിൽ തുടർച്ചയാണ്.
2. ഒരു നിശ്ചിത ഇടവേളയിൽ നൽകിയിരിക്കുന്ന f(x) ഉം φ(x) യും ഈ ഇടവേളയുടെ x 0 എന്ന ബിന്ദുവിൽ തുടർച്ചയാണെങ്കിൽ, ഫംഗ്ഷനുകളും ഈ ഘട്ടത്തിൽ തുടർച്ചയായിരിക്കും.
3. X-ൽ നിന്നുള്ള x 0 പോയിന്റിൽ y=f(x) തുടർച്ചയാണെങ്കിൽ, z=φ(y) എന്നത് Y-യിൽ നിന്നുള്ള അനുബന്ധ പോയിന്റിൽ y 0 =f(x 0) തുടർച്ചയാണെങ്കിൽ, പിന്നെ സങ്കീർണ്ണമായ പ്രവർത്തനം x 0 പോയിന്റിൽ z=φ(f(x)) തുടർച്ചയായിരിക്കും.

ഫംഗ്ഷൻ ബ്രേക്കുകളും അവയുടെ വർഗ്ഗീകരണവും

x 0 പോയിന്റിലെ f(x) ഫംഗ്‌ഷന്റെ തുടർച്ചയുടെ ഒരു അടയാളം തുല്യതയാണ്, ഇത് മൂന്ന് വ്യവസ്ഥകളുടെ സാന്നിധ്യം സൂചിപ്പിക്കുന്നു:
1) x 0 പോയിന്റിൽ f(x) നിർവചിച്ചിരിക്കുന്നു;
2) ;
3) .
ഈ ആവശ്യകതകളിലൊന്നെങ്കിലും ലംഘിക്കപ്പെട്ടാൽ, x 0-നെ ഫംഗ്‌ഷന്റെ ബ്രേക്ക് പോയിന്റ് എന്ന് വിളിക്കുന്നു. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ഈ പ്രവർത്തനം തുടർച്ചയായി ഇല്ലാത്ത ഒരു പോയിന്റാണ് ബ്രേക്ക് പോയിന്റ്. ബ്രേക്ക് പോയിന്റുകളുടെ നിർവചനത്തിൽ നിന്ന്, ഒരു ഫംഗ്ഷന്റെ ബ്രേക്ക് പോയിന്റുകൾ ഇവയാണ്:
a) f(x) തുടർച്ചയുടെ സ്വത്ത് നഷ്‌ടപ്പെടുന്ന ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ ഉൾപ്പെടുന്ന പോയിന്റുകൾ,
b) ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിന്റെ രണ്ട് ഇടവേളകളുടെ അടുത്തുള്ള പോയിന്റുകളാണ് f(x) ന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ ഉൾപ്പെടാത്ത പോയിന്റുകൾ.
ഉദാഹരണത്തിന്, ഒരു ഫംഗ്‌ഷനായി, പോയിന്റ് x=0 ഒരു ബ്രേക്ക് പോയിന്റാണ്, കാരണം ഈ പോയിന്റിലെ ഫംഗ്‌ഷൻ നിർവചിച്ചിട്ടില്ല, കൂടാതെ ഫംഗ്‌ഷൻ x=1 എന്ന പോയിന്റിൽ ഒരു വിച്ഛേദമുണ്ട്, അത് f(x) ന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിന്റെ രണ്ട് ഇടവേളകളോട് (-∞,1) (1,∞) അടുത്താണ്, അത് നിലവിലില്ല.

ബ്രേക്ക് പോയിന്റുകൾക്കായി ഇനിപ്പറയുന്ന വർഗ്ഗീകരണം സ്വീകരിച്ചിരിക്കുന്നു.
1) x 0 എന്ന ബിന്ദുവിൽ പരിമിതികളുണ്ടെങ്കിൽ ഒപ്പം , എന്നാൽ f(x 0 +0)≠f(x 0 -0), തുടർന്ന് x 0 എന്ന് വിളിക്കുന്നു ആദ്യ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റ് , എന്നും വിളിക്കപ്പെടുന്നു ഫംഗ്ഷൻ ജമ്പ് .

ഉദാഹരണം 2. പ്രവർത്തനം പരിഗണിക്കുക
x=2 എന്ന ബിന്ദുവിൽ മാത്രമേ ഫംഗ്‌ഷൻ തകർക്കാൻ കഴിയൂ (മറ്റ് പോയിന്റുകളിൽ ഇത് ഏതൊരു ബഹുപദം പോലെയും തുടർച്ചയായിരിക്കും).
ഞങ്ങൾ കണ്ടെത്തും , . ഏകപക്ഷീയമായ പരിധികൾ പരിമിതമാണ്, എന്നാൽ പരസ്പരം തുല്യമല്ലാത്തതിനാൽ, x=2 എന്ന പോയിന്റിൽ ഫംഗ്‌ഷന് ആദ്യ തരത്തിലുള്ള ഒരു വിച്ഛേദം ഉണ്ടായിരിക്കും. ശ്രദ്ധിക്കുക, അത് , അതിനാൽ ഈ ഘട്ടത്തിലെ പ്രവർത്തനം വലതുവശത്ത് തുടർച്ചയായി തുടരുന്നു (ചിത്രം 2).
2) രണ്ടാമത്തെ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റുകൾ ഏകപക്ഷീയമായ പരിധികളിൽ ഒന്നെങ്കിലും ∞ ന് തുല്യമായതോ നിലവിലില്ലാത്തതോ ആയ പോയിന്റുകളെ വിളിക്കുന്നു.

ഉദാഹരണം 3. x=0 ഒഴികെയുള്ള x ന്റെ എല്ലാ മൂല്യങ്ങൾക്കും y=2 1/ x എന്ന ഫംഗ്‌ഷൻ തുടർച്ചയായതാണ്. നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്താം: , , അതിനാൽ x=0 എന്നത് രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിച്ഛേദ പോയിന്റാണ് (ചിത്രം 3).
3) പോയിന്റ് x=x 0 എന്ന് വിളിക്കുന്നു നീക്കം ചെയ്യാവുന്ന ബ്രേക്ക് പോയിന്റ് , f(x 0 +0)=f(x 0 -0)≠f(x 0) ആണെങ്കിൽ.
സജ്ജീകരിക്കുന്നതിലൂടെ ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെ മൂല്യം മാറ്റാൻ (പുനർ നിർവചിക്കുക അല്ലെങ്കിൽ പുനർ നിർവചിക്കുക) മതി എന്ന അർത്ഥത്തിൽ ഞങ്ങൾ വിടവ് "ഒഴിവാക്കും", കൂടാതെ x 0 പോയിന്റിൽ ഫംഗ്ഷൻ തുടർച്ചയായി മാറും.
ഉദാഹരണം 4. എന്ന് അറിയപ്പെടുന്നു , ഈ പരിധി x പൂജ്യത്തിലേക്കുള്ള പ്രവണതയെ ആശ്രയിക്കുന്നില്ല. എന്നാൽ x=0 എന്ന പോയിന്റിലെ ഫംഗ്‌ഷൻ നിർവചിച്ചിട്ടില്ല. f(0)=1 സജ്ജീകരിച്ച് ഞങ്ങൾ ഫംഗ്‌ഷനെ പുനർനിർവചിക്കുകയാണെങ്കിൽ, ഈ ഘട്ടത്തിൽ അത് തുടർച്ചയായി മാറുന്നു (മറ്റ് പോയിന്റുകളിൽ ഇത് തുടർച്ചയായ പ്രവർത്തനങ്ങളായ sinx, x എന്നിവയുടെ ഘടകമായി തുടരുന്നു).
ഉദാഹരണം 5. ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച പരിശോധിക്കുക .
പരിഹാരം. y=x 3, y=2x എന്നീ ഫംഗ്‌ഷനുകൾ സൂചിപ്പിച്ചിരിക്കുന്ന ഇടവേളകളിൽ ഉൾപ്പെടെ എല്ലായിടത്തും നിർവചിക്കപ്പെട്ടതും തുടർച്ചയായതുമാണ്. നമുക്ക് x=0 ഇടവേളകളുടെ ജംഗ്ഷൻ പോയിന്റ് പരിശോധിക്കാം:
, , നമുക്ക് അത് ലഭിക്കുന്നു, അതായത് x=0 എന്ന ബിന്ദുവിൽ പ്രവർത്തനം തുടർച്ചയായി പ്രവർത്തിക്കുന്നു.
നിർവ്വചനം. ആദ്യ തരത്തിലുള്ള അല്ലെങ്കിൽ നീക്കം ചെയ്യാവുന്ന വിച്ഛേദിക്കുന്നതിനുള്ള പരിമിതമായ സംഖ്യകൾ ഒഴികെയുള്ള ഒരു ഇടവേളയിൽ തുടർച്ചയായി നടക്കുന്ന ഒരു ഫംഗ്ഷനെ ഈ ഇടവേളയിൽ പീസ്വൈസ് തുടർച്ചയായി വിളിക്കുന്നു.

തുടർച്ചയായ പ്രവർത്തനങ്ങളുടെ ഉദാഹരണങ്ങൾ

ഉദാഹരണം 1. x=2 എന്ന പോയിന്റിൽ ഒഴികെ (-∞,+∞) ഫംഗ്‌ഷൻ നിർവചിക്കപ്പെട്ടതും തുടർച്ചയായതുമാണ്. ബ്രേക്ക് തരം നിർണ്ണയിക്കാം. എന്തുകൊണ്ടെന്നാല് ഒപ്പം , പിന്നീട് x=2 എന്ന ബിന്ദുവിൽ രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമം ഉണ്ട് (ചിത്രം 6).
ഉദാഹരണം 2. ഛേദം പൂജ്യമായിരിക്കുന്ന x=0 ഒഴികെയുള്ള എല്ലാ x-നും ഫംഗ്ഷൻ നിർവചിക്കപ്പെട്ടതും തുടർച്ചയായതുമാണ്. x=0 എന്ന പോയിന്റിൽ നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്താം:
ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും വ്യത്യസ്‌തവുമാണ്, അതിനാൽ, x=0 ആദ്യ തരത്തിലുള്ള ഒരു വിച്ഛേദ പോയിന്റാണ് (ചിത്രം 7).
ഉദാഹരണം 3. ഫംഗ്‌ഷന് ഏതൊക്കെ പോയിന്റുകളിലാണെന്നും ഏത് തരത്തിലുള്ള വിച്ഛേദനങ്ങളാണെന്നും നിർണ്ണയിക്കുക
ഈ ഫംഗ്‌ഷൻ [-2,2]-ൽ നിർവ്വചിച്ചിരിക്കുന്നു. യഥാക്രമം [-2,0] എന്നീ ഇടവേളകളിൽ x 2, 1/x എന്നിവ തുടർച്ചയായതിനാൽ, ഇടവേളകളുടെ ജംഗ്ഷനിൽ, അതായത് x=0 എന്ന ബിന്ദുവിൽ മാത്രമേ വിച്ഛേദനം ഉണ്ടാകൂ. എന്നതിനാൽ, x=0 എന്നത് രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിച്ഛേദ പോയിന്റാണ്.

ഉദാഹരണം 4. പ്രവർത്തന വിടവുകൾ ഇല്ലാതാക്കാൻ കഴിയുമോ:
എ) പോയിന്റ് x=2;
b) പോയിന്റ് x=2;
വി) പോയിന്റിൽ x=1?
പരിഹാരം. ഉദാഹരണം സംബന്ധിച്ച് a) x=2 എന്ന പോയിന്റിലെ എഫ്(x) വിച്ഛേദനം ഇല്ലാതാക്കാൻ കഴിയില്ലെന്ന് നമുക്ക് ഉടനടി പറയാൻ കഴിയും, കാരണം ഈ ഘട്ടത്തിൽ അനന്തമായ ഏകപക്ഷീയമായ പരിധികളുണ്ട് (ഉദാഹരണം 1 കാണുക).
b) ഫംഗ്‌ഷൻ g(x) ന് x=2 എന്ന പോയിന്റിൽ പരിമിതമായ ഏകപക്ഷീയമായ പരിധികൾ ഉണ്ടെങ്കിലും

(,),

എന്നാൽ അവ പൊരുത്തപ്പെടുന്നില്ല, അതിനാൽ വിടവ് ഇല്ലാതാക്കാനും കഴിയില്ല.
c) x=1 എന്ന വിരാമ പോയിന്റിലെ ഫംഗ്‌ഷൻ φ(x) ന് തുല്യമായ ഏകപക്ഷീയമായ പരിമിത പരിധികളുണ്ട്: . അതിനാൽ, f(1)=2 എന്നതിനുപകരം f(1)=1 ഇട്ടുകൊണ്ട് x=1-ൽ ഫംഗ്‌ഷൻ പുനർനിർവചിക്കുന്നതിലൂടെ വിടവ് ഇല്ലാതാക്കാം.

ഉദാഹരണം 5. Dirichlet ഫംഗ്‌ഷൻ കാണിക്കുക

സംഖ്യാ അച്ചുതണ്ടിലെ ഓരോ ബിന്ദുവിലും തുടർച്ചയായി നിൽക്കുന്നില്ല.
പരിഹാരം. (-∞,+∞) ൽ നിന്നുള്ള ഏതെങ്കിലും പോയിന്റ് x 0 ആയിരിക്കട്ടെ. അതിന്റെ ഏത് അയൽപക്കത്തിലും യുക്തിസഹവും യുക്തിരഹിതവുമായ പോയിന്റുകൾ ഉണ്ട്. ഇതിനർത്ഥം x 0 ന്റെ ഏത് അയൽപക്കത്തിലും ഫംഗ്‌ഷന് 0, 1 എന്നിവയ്ക്ക് തുല്യമായ മൂല്യങ്ങൾ ഉണ്ടായിരിക്കും. ഈ സാഹചര്യത്തിൽ, x 0 പോയിന്റിൽ ഇടത്തോ വലത്തോട്ടോ ഉള്ള ഫംഗ്‌ഷന്റെ പരിധി ഉണ്ടായിരിക്കില്ല, അതായത് യഥാർത്ഥ അച്ചുതണ്ടിലെ ഓരോ ബിന്ദുവിലും ഡിറിച്ലെറ്റ് ഫംഗ്‌ഷന് രണ്ടാമത്തെ തരത്തിലുള്ള വിച്ഛേദനങ്ങളുണ്ടെന്ന്.

ഉദാഹരണം 6. ഫംഗ്ഷൻ ബ്രേക്ക് പോയിന്റുകൾ കണ്ടെത്തുക

അവയുടെ തരം നിർണ്ണയിക്കുക.
പരിഹാരം. പൊട്ടുന്നതായി സംശയിക്കുന്ന പോയിന്റുകൾ x 1 =2, x 2 =5, x 3 =3 എന്നിവയാണ്.
ബിന്ദുവിൽ x 1 =2 f(x) ന് രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമം ഉണ്ട്
.
പോയിന്റ് x 2 =5 എന്നത് തുടർച്ചയുടെ ഒരു ബിന്ദുവാണ്, കാരണം ഈ ഘട്ടത്തിലും അതിന്റെ സമീപത്തുമുള്ള ഫംഗ്‌ഷന്റെ മൂല്യം നിർണ്ണയിക്കുന്നത് രണ്ടാമത്തെ വരിയാണ്, അല്ലാതെ ആദ്യ വരിയല്ല: .
നമുക്ക് x 3 =3 പോയിന്റ് പരിശോധിക്കാം: , അതിൽ നിന്ന് x=3 ആദ്യ തരത്തിലുള്ള ഒരു വിച്ഛേദ പോയിന്റാണ്.

വേണ്ടി സ്വതന്ത്ര തീരുമാനം.
തുടർച്ചയ്ക്കായി ഫംഗ്‌ഷനുകൾ പരിശോധിക്കുകയും നിർത്തലാക്കുന്ന പോയിന്റുകളുടെ തരം നിർണ്ണയിക്കുകയും ചെയ്യുക:
1) ; ഉത്തരം: x=-1 - നീക്കം ചെയ്യാവുന്ന വിരാമത്തിന്റെ പോയിന്റ്;
2) ; ഉത്തരം: x=8 എന്ന ബിന്ദുവിൽ രണ്ടാമത്തെ തരത്തിന്റെ തുടർച്ച;
3) ; ഉത്തരം: x=1-ൽ ആദ്യ തരത്തിലുള്ള നിർത്തലാക്കൽ;
4)
ഉത്തരം: x 1 =-5 എന്ന ബിന്ദുവിൽ നീക്കം ചെയ്യാവുന്ന വിടവുണ്ട്, x 2 =1 ൽ രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിടവും x 3 =0 എന്ന ബിന്ദുവിൽ ആദ്യ തരത്തിലുള്ള വിടവുമുണ്ട്.
5) എ സംഖ്യ എങ്ങനെ തിരഞ്ഞെടുക്കണം, അങ്ങനെ ഫംഗ്‌ഷൻ

x=0-ൽ തുടർച്ചയായിരിക്കുമോ?
ഉത്തരം: എ=2.
6) ഫംഗ്‌ഷൻ ആകുന്നതിന് എ നമ്പർ തിരഞ്ഞെടുക്കുന്നത് സാധ്യമാണോ

x=2-ൽ തുടർച്ചയായിരിക്കുമോ?
ഉത്തരം: ഇല്ല.

ഒരു ഘട്ടത്തിൽ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച. ഫംഗ്ഷൻ y = f(x ) അൺപ്രീ എന്ന് വിളിക്കുന്നു

പോയിന്റ് x 0-ൽ ഞെട്ടിയുണ്ടെങ്കിൽ:

1) പോയിന്റിന്റെ ചില അയൽപക്കങ്ങളിൽ ഈ പ്രവർത്തനം നിർവ്വചിച്ചിരിക്കുന്നു x 0 ;

2) ഒരു പരിധിയുണ്ട് f(x);

→ x 0

3) ഈ പരിധി മൂല്യത്തിന് തുല്യമാണ്പോയിന്റ് x 0-ലെ പ്രവർത്തനങ്ങൾ, അതായത്. limf (x )= f (x 0 ) .
		x→x0
അവസാന വ്യവസ്ഥ ലിം എന്ന അവസ്ഥയ്ക്ക് തുല്യമാണ്		y = 0, ഇവിടെ x = x - x 0 - എപ്പോൾ
	x→ 0
ആർഗ്യുമെന്റിന്റെ ഭ്രമണം, y = f (x 0 +	x )− f (x 0 ) - ഫംഗ്‌ഷന്റെ വർദ്ധനവ്, അനുബന്ധം
വാദം വർദ്ധിപ്പിക്കുന്നു	x, അതായത്. പ്രവർത്തനം	f(x) x 0-ൽ തുടർച്ചയാണ്

ഈ ഘട്ടത്തിൽ ആർഗ്യുമെന്റിന്റെ അനന്തമായ ഇൻക്രിമെന്റ് ഫംഗ്ഷന്റെ അനന്തമായ ഇൻക്രിമെന്റുമായി പൊരുത്തപ്പെടുന്നെങ്കിൽ മാത്രം.

വൺ-വേ തുടർച്ച. y = f (x) എന്ന ഫംഗ്‌ഷനെ തുടർച്ചയായി വിളിക്കുന്നു

ഇടത് വശത്ത് പോയിന്റ്x 0-ൽ അത് ചില അർദ്ധ-ഇടവേളയിൽ (a ;x 0 ] നിർവചിച്ചിട്ടുണ്ടെങ്കിൽ

ഒപ്പം lim f (x)= f (x 0).

x→ x0 − 0

ഒരു ഫംഗ്‌ഷൻ y = f (x) എന്നത് op- ആണെങ്കിൽ x 0 എന്ന ബിന്ദുവിൽ ശരിയായ തുടർച്ചയായതായി പറയപ്പെടുന്നു.

ഒരു നിശ്ചിത അർദ്ധ ഇടവേളയിൽ വിതരണം ചെയ്യപ്പെടുന്നു [ x 0 ;a ) ഒപ്പം limf (x )= f (x 0 ) .

x→ x0 + 0

ഫംഗ്‌ഷൻ y = f(x)		പോയിന്റ് x 0-ൽ തുടർച്ചയായി			പിന്നെ അവൾ എപ്പോൾ മാത്രം
തുടർച്ചയായ
lim f (x)= limf (x)= limf (x)= f (x 0).
x→ x0 + 0	x→ x0 − 0	x→x0

ഒരു സെറ്റിൽ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച. y = f (x) എന്ന ഫംഗ്‌ഷനെ വിളിക്കുന്നു

സെറ്റിൽ തുടർച്ചയായിഈ സെറ്റിന്റെ എല്ലാ പോയിന്റിലും ഇത് തുടർച്ചയായി ആണെങ്കിൽ X. കൂടാതെ, സംഖ്യാ അച്ചുതണ്ടിന്റെ ഒരു നിശ്ചിത ഇടവേളയുടെ അവസാനത്തിൽ ഒരു ഫംഗ്ഷൻ നിർവചിച്ചിട്ടുണ്ടെങ്കിൽ, ഈ ഘട്ടത്തിലെ തുടർച്ചയെ വലത് അല്ലെങ്കിൽ ഇടത് വശത്ത് തുടർച്ചയായി മനസ്സിലാക്കുന്നു. പ്രത്യേകിച്ചും, y = f (x) ഫംഗ്‌ഷനെ നോൺ എന്ന് വിളിക്കുന്നു

സെഗ്മെന്റിൽ തുടർച്ചയായി [a; b] അവൾ ആണെങ്കിൽ

1) ഇടവേളയുടെ ഓരോ പോയിന്റിലും തുടർച്ചയായി(എ;ബി);

2) ഒരു ബിന്ദുവിൽ തുടർച്ചയായി ശരിയാണ്എ;

3) ഒരു ഘട്ടത്തിൽ തുടർച്ചയായി അവശേഷിക്കുന്നുബി.

ഫംഗ്ഷൻ ബ്രേക്ക് പോയിന്റുകൾ. y = f (x) എന്ന ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ ഉൾപ്പെടുന്ന പോയിന്റ് x 0 അല്ലെങ്കിൽ ഈ ഡൊമെയ്‌നിന്റെ അതിർത്തി പോയിന്റ് എന്ന് വിളിക്കപ്പെടുന്നു

ഈ ഫംഗ്‌ഷന്റെ ബ്രേക്ക് പോയിന്റ്, iff(x) ആ ഘട്ടത്തിൽ തുടർച്ചയായില്ല.

വിച്ഛേദിക്കുന്നതിനുള്ള പോയിന്റുകൾ ഒന്നും രണ്ടും തരത്തിൽ വിച്ഛേദിക്കപ്പെട്ടിരിക്കുന്നു:

1) പരിമിതമായ പരിധികൾ ഉണ്ടെങ്കിൽ lim f (x )= f (x 0 - 0) കൂടാതെ

x→ x0 − 0

	f (x)= f (x 0 + 0), കൂടാതെ മൂന്ന് സംഖ്യകളും f (x 0 - 0), f (x 0 + 0),		f (x 0 ) തുല്യമാണ്
x→ x0 + 0
അവർക്കിടയിൽ, പിന്നെ x 0		ആദ്യത്തെ തരത്തിലുള്ള ഒരു വിച്ഛേദ പോയിന്റ് എന്ന് വിളിക്കുന്നു.
	പ്രത്യേകിച്ചും, x 0 എന്ന പോയിന്റിലെ ഫംഗ്‌ഷന്റെ ഇടത്, വലത് പരിധികൾ ആണെങ്കിൽ		തമ്മിൽ തുല്യമാണ്
	സ്വയം, പക്ഷേ	ഈ ഘട്ടത്തിലെ പ്രവർത്തന മൂല്യത്തിന് തുല്യമല്ല:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , തുടർന്ന് x 0 എന്നത് നീക്കം ചെയ്യാവുന്ന വിച്ഛേദിക്കുന്ന പോയിന്റ് എന്ന് വിളിക്കുന്നു.

ഈ സാഹചര്യത്തിൽ, f (x 0 )= A സജ്ജീകരിക്കുന്നതിലൂടെ, നിങ്ങൾക്ക് പോയിന്റ് x 0-ൽ ഫംഗ്ഷൻ പരിഷ്കരിക്കാനാകും.

അങ്ങനെ അത് തുടർച്ചയായി മാറുന്നു ( തുടർച്ചയായി പ്രവർത്തനത്തെ പുനർനിർവചിക്കുക). f (x 0 + 0)− f (x 0 - 0) എന്ന വ്യത്യാസത്തെ വിളിക്കുന്നു ഒരു ഘട്ടത്തിൽ ഒരു ഫംഗ്‌ഷന്റെ ജമ്പ് x 0

നീക്കം ചെയ്യാവുന്ന വിരാമ പോയിന്റിലെ ഫംഗ്‌ഷൻ ജമ്പ് പൂജ്യമാണ്.

2) ആദ്യത്തെ തരത്തിലുള്ള വിച്ഛേദിക്കാത്ത പോയിന്റുകളെ വിളിക്കുന്നു രണ്ടാമത്തെ തരത്തിലുള്ള ബ്രേക്ക് പോയിന്റുകൾ. രണ്ടാമത്തെ തരത്തിലുള്ള വിച്ഛേദിക്കുന്ന പോയിന്റുകളിൽ, f (x 0 - 0), f (x 0 + 0) എന്നീ ഏകപക്ഷീയ പരിധികളിൽ ഒന്നെങ്കിലും നിലവിലില്ല അല്ലെങ്കിൽ അനന്തമാണ്.

ഒരു ഘട്ടത്തിൽ തുടർച്ചയായ പ്രവർത്തനങ്ങളുടെ ഗുണവിശേഷതകൾ.

		f(x)	g (x) എന്നിവ x 0 എന്ന ബിന്ദുവിൽ തുടർച്ചയായിരിക്കും, തുടർന്ന് പ്രവർത്തനങ്ങൾ
f(x) ±g(x),	f(x)g(x) കൂടാതെ	f(x)	(ഇവിടെ g (x)≠ 0) പോയിന്റ് x-ലും തുടർച്ചയായിരിക്കും.
		g(x)

2) u (x) എന്ന ഫംഗ്‌ഷൻ x 0 പോയിന്റിൽ തുടർച്ചയും f (u) ഫംഗ്‌ഷൻ തുടർച്ചയായും ആണെങ്കിൽ

u 0 = u (x 0) എന്ന ബിന്ദുവിൽ, പിന്നെ f (u (x)) എന്ന കോംപ്ലക്സ് ഫംഗ്ഷൻ x 0 എന്ന ബിന്ദുവിൽ തുടർച്ചയായിരിക്കും.

3) എല്ലാ അടിസ്ഥാന പ്രാഥമിക പ്രവർത്തനങ്ങളും (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) ഓരോന്നിലും തുടർച്ചയായതാണ്

അവരുടെ നിർവ്വചന മേഖലകൾ വരെ.

പ്രോപ്പർട്ടികൾ 1)-3) എല്ലാ എലിമെന്ററി ഫംഗ്ഷനുകളും (അടിസ്ഥാന പ്രാഥമിക ഫംഗ്ഷനുകളിൽ നിന്ന് പരിമിതമായ എണ്ണം ഗണിത പ്രവർത്തനങ്ങളും കോമ്പോസിഷൻ ഓപ്പറേഷനുകളും ഉപയോഗിച്ച് ലഭിക്കുന്ന പ്രവർത്തനങ്ങൾ) അവയുടെ നിർവചനത്തിന്റെ ഓരോ പോയിന്റിലും തുടർച്ചയായി തുടരുന്നു.

ഒരു ഇടവേളയിൽ തുടർച്ചയായ പ്രവർത്തനങ്ങളുടെ ഗുണവിശേഷതകൾ.

1) (ഇന്റർമീഡിയറ്റ് മൂല്യ സിദ്ധാന്തം) ഫംഗ്ഷൻ f(x) നിർവചിക്കട്ടെ

ഓൺ കൂടാതെ സെഗ്‌മെന്റിൽ തുടർച്ചയായി തുടരുന്നു [a;b]. അപ്പോൾ ഏത് നമ്പറിനും സി

f (a), f (b), (f (a) എന്നീ സംഖ്യകൾക്കിടയിൽ< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (ബോൾസാനോ-കൗച്ചി സിദ്ധാന്തം

സെഗ്‌മെന്റിൽ [a;b] തുടർച്ചയായി തുടരുകയും അതിന്റെ അറ്റത്ത് വ്യത്യസ്ത ചിഹ്നങ്ങളുടെ മൂല്യങ്ങൾ എടുക്കുകയും ചെയ്യുന്നു.

അപ്പോൾ f (x 0)= 0 എന്ന ഒരു പോയിന്റെങ്കിലും x 0 [a; b] ഉണ്ട്.

3) (1st വെയർസ്ട്രാസിന്റെ സിദ്ധാന്തം) ഫംഗ്ഷൻ f (x) നിർവചിക്കട്ടെ

സെഗ്മെന്റിൽ കീറി [a;b]. അപ്പോൾ ഈ ഫംഗ്‌ഷൻ ഈ സെഗ്‌മെന്റിൽ പരിമിതപ്പെടുത്തിയിരിക്കുന്നു.

4) (രണ്ടാമത് വെയർസ്ട്രാസിന്റെ സിദ്ധാന്തം) ഫംഗ്ഷൻ f (x) നിർവചിക്കട്ടെ

സെഗ്മെന്റിൽ തിരക്ക്		[a;b] . അപ്പോൾ ഈ ഫംഗ്‌ഷൻ [a; b] ഇടവേളയിൽ എത്തുന്നു
ഏറ്റവും വലിയ		കുറഞ്ഞത്	മൂല്യങ്ങൾ, അതായത്.	നിലവിലുണ്ട്
x1, x2 [a; b] ,		ഏതിനും	പോയിന്റുകൾ x [a;b]	ന്യായമായ	അസമത്വങ്ങൾ

f (x 1 )≤ f (x )≤ f (x 2 ) .

ഉദാഹരണം 5.17. തുടർച്ചയുടെ നിർവചനം ഉപയോഗിച്ച്, സംഖ്യാരേഖയിലെ ഒരു അനിയന്ത്രിതമായ പോയിന്റിൽ x 0 എന്ന ഫംഗ്ഷൻ y = 3x 2 + 2x - 5 തുടർച്ചയായി തുടരുന്നുവെന്ന് തെളിയിക്കുക.

പരിഹാരം: രീതി 1: സംഖ്യയുടെ അച്ചുതണ്ടിൽ x 0 ഒരു ഏകപക്ഷീയ ബിന്ദുവായിരിക്കട്ടെ. നിങ്ങൾ-

ഫംഗ്‌ഷനുകളുടെ ആകെത്തുകയുടെയും ഗുണനത്തിന്റെയും പരിധിയിൽ സിദ്ധാന്തങ്ങൾ പ്രയോഗിച്ച്, ഫംഗ്‌ഷന്റെ (x) പരിധി x → x 0 ആയി ഞങ്ങൾ ആദ്യം കണക്കാക്കുന്നു:

lim f (x )= lim(3x 2 + 2x - 5)= 3(limx )2 + 2 limx - 5= 3x 2							− 5.
x→x0	x→x0	x→x0	x→x0
തുടർന്ന് x:f (x)= 3x 2 എന്ന പോയിന്റിൽ ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ കണക്കാക്കുന്നു							− 5 .
ലഭിച്ച ഫലങ്ങൾ താരതമ്യം ചെയ്യുമ്പോൾ, ഞങ്ങൾ കാണുന്നു				lim f (x)= f (x 0) ഏത് പ്രകാരം
				x→x0

നിർവചനം x 0 പോയിന്റിൽ പരിഗണനയിലുള്ള ഫംഗ്‌ഷന്റെ തുടർച്ച എന്നാണ് അർത്ഥമാക്കുന്നത്.

രീതി 2: അനുവദിക്കുക		x - പോയിന്റ്x 0 ലെ ആർഗ്യുമെന്റിന്റെ വർദ്ധനവ്. നമുക്ക് കത്തിടപാടുകൾ കണ്ടെത്താം
ഉചിതമായ	ഇൻക്രിമെന്റും			y = f(x0 + x) - f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x - 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
ആർഗ്യുമെന്റിന്റെ വർദ്ധനവ് ഫംഗ്ഷൻ ഇൻക്രിമെന്റിന്റെ പരിധി കണക്കാക്കാം
		പരിശ്രമിക്കുന്നു

	y = ലിം (6x + 2)		x + (x )2 = (6x + 2) ലിം		x + (limx)2 = 0.
x→ 0	x→ 0			x→ 0	x→ 0

അങ്ങനെ, lim y = 0, അതായത് നിർവചനം തുടർച്ച

x→ 0

ഏതെങ്കിലും x 0 R-നുള്ള പ്രവർത്തനങ്ങൾ.

ഉദാഹരണം 5.18. f (x) ഫംഗ്‌ഷന്റെ ഡിസ്‌കണ്ടിന്യുറ്റി പോയിന്റുകൾ കണ്ടെത്തി അവയുടെ തരം നിർണ്ണയിക്കുക. IN

ഒരു നീക്കം ചെയ്യാവുന്ന നിർത്തലാക്കലിന്റെ കാര്യത്തിൽ, തുടർച്ചയായി പ്രവർത്തനം നിർവ്വചിക്കുക:

1) f (x) = 1− x 2 ൽ x< 3;

5x ആകുമ്പോൾ x ≥ 3

2) f (x)= x 2 + 4 x + 3;

x+1

	f(x)=
		x4 (x− 2)
	f(x)= ആർക്റ്റാൻ
			(x - 5)

പരിഹാരം: 1) ഈ ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌ൻ മുഴുവൻ സംഖ്യയാണ്

y അക്ഷം (−∞ ;+∞) . ഇടവേളകളിൽ (−∞ ;3) ,(3;+∞ ) പ്രവർത്തനം തുടർച്ചയായി നടക്കുന്നു. പ്രവർത്തനത്തിന്റെ അനലിറ്റിക്കൽ സ്പെസിഫിക്കേഷൻ മാറുന്ന പോയിന്റിൽ x = 3-ൽ മാത്രമേ ഒരു വിച്ഛേദനം സാധ്യമാകൂ.

സൂചിപ്പിച്ച പോയിന്റിൽ ഫംഗ്‌ഷന്റെ ഏകപക്ഷീയമായ പരിധികൾ നമുക്ക് കണ്ടെത്താം:

f (3− 0)= ലിം (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= ലിം 5x = 15.

x →3 +0

ഇടത്, വലത് പരിധികൾ പരിമിതമാണെന്ന് ഞങ്ങൾ കാണുന്നു, അതിനാൽ x = 3
വിള്ളൽ I			f(x). ഫംഗ്‌ഷൻ കുതിക്കുക
f (3+ 0)− f (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , അതിനാൽ പോയിന്റിൽ		x = 3

f(x) ശരിയായ തുടർച്ചയായതാണ്.

2) പോയിന്റ് ഒഴികെ മുഴുവൻ സംഖ്യാ രേഖയിലും പ്രവർത്തനം തുടർച്ചയായാണ് x = - 1, അതിൽ നിർവചിച്ചിട്ടില്ല. ന്യൂമറേറ്റർ വികസിപ്പിച്ചുകൊണ്ട് f (x) എന്നതിനുള്ള എക്സ്പ്രഷൻ രൂപാന്തരപ്പെടുത്താം

ഘടകങ്ങളായി ഭിന്നസംഖ്യകൾ:		f(x)=			4 x +3			(x + 1)(x + 3)	x ≠ − 1 ന് X + 3.
					x+1			x+1
x = − 1 എന്ന പോയിന്റിൽ ഫംഗ്‌ഷന്റെ ഏകപക്ഷീയമായ പരിധികൾ നമുക്ക് കണ്ടെത്താം:
	f(x)=ലിം	f (x )= ലിം(x + 3)= 2 .
x →−1−0	x →−1 +0		x →−1

പഠനത്തിന് കീഴിലുള്ള പോയിന്റിലെ ഫംഗ്‌ഷന്റെ ഇടത്, വലത് പരിധികൾ നിലവിലുണ്ടെന്ന് ഞങ്ങൾ കണ്ടെത്തി, അവ പരിമിതവും പരസ്പരം തുല്യവുമാണ്, അതിനാൽ x = - 1 ഒരു നീക്കം ചെയ്യാവുന്ന പോയിന്റാണ്

നേർരേഖ y = x + 3 "കുളിച്ച" പോയിന്റ് M (− 1;2) . പ്രവർത്തനം സ്ഥിരമാകുന്നതിന്

തുടർച്ചയായി, നമ്മൾ f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 ഇടണം.

അങ്ങനെ, x = - 1 എന്ന പോയിന്റിലെ തുടർച്ചയിലൂടെ f (x) കൂടുതൽ നിർവചിച്ചതിന് ശേഷം, ഞങ്ങൾ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിനൊപ്പം f * (x)= x + 3 എന്ന ഫംഗ്ഷൻ ലഭിച്ചു (−∞ ;+∞ ) .

3) ഈ പ്രവർത്തനംഎല്ലാവർക്കും നിർവചിക്കപ്പെട്ടതും തുടർച്ചയായതും x പോയിന്റുകൾ ഒഴികെ

x = 0,x = 2, ഇതിൽ ഭിന്നസംഖ്യയുടെ ഡിനോമിനേറ്റർ പൂജ്യമാകും.

പോയിന്റ് x = 0 പരിഗണിക്കുക:

പൂജ്യത്തിന്റെ മതിയായ അയൽപക്കത്തിൽ ഫംഗ്‌ഷൻ മാത്രമേ എടുക്കൂ

	നെഗറ്റീവ് മൂല്യങ്ങൾക്ക്, പിന്നെ f (− 0)= lim			= -∞ = f (+0)	ആ. ഡോട്ട്
			(x - 2)
	x →−0
	x = 0 എന്നത് രണ്ടാമത്തെ തരത്തിലുള്ള ഫംഗ്‌ഷന്റെ ഒരു വിച്ഛേദ പോയിന്റാണ്		f(x).

ഇപ്പോൾ പോയിന്റ് x = 2 പരിഗണിക്കുക:

ഫംഗ്ഷൻ പരിഗണിക്കുന്നതിന്റെ ഇടതുവശത്ത് നെഗറ്റീവ് മൂല്യങ്ങൾ എടുക്കുന്നു

	പോയിന്റും പോസിറ്റീവും വലതുവശത്താണ്, അതിനാൽ				f (2− 0)=			= −∞,
							x4 (x− 2)
						x →2 −0
	f (2+ 0)= ലിം			= +∞ . മുമ്പത്തെ കാര്യത്തിലെന്നപോലെ, pointx = 2-ൽ
			(x - 2)
	x →2 +0

tion ന് ഇടത് അല്ലെങ്കിൽ വലത് പരിധികളില്ല, അതായത്. ഈ ഘട്ടത്തിൽ ഒരു തരം II വിള്ളൽ അനുഭവിക്കുന്നു.

x = 5 .

f (5− 0)= lim arctan

π ,f (5+ 0)= lim arctan

x = 5

(x - 5)

(x - 5)

x →5 -0

x →5 +0

കാ വിള്ളൽ

f (5+ 0)− f (5− 0)=

π − (−

π )= π (ചിത്രം 5.2 കാണുക).

സ്വതന്ത്രമായി പരിഹരിക്കാനുള്ള പ്രശ്നങ്ങൾ

5.174 നിർവചനം മാത്രം ഉപയോഗിച്ച്, f (x) in ഫംഗ്‌ഷന്റെ തുടർച്ച തെളിയിക്കുക

ഓരോ പോയിന്റും x 0 R:

a) f(x) = c= const;		b) f (x)= x;
c) f (x)= x 3;		d) f (x)= 5x 2 - 4x + 1;
e) f (x)= sinx.
5.175 പ്രവർത്തനം തെളിയിക്കുക	f(x) = x2	1 x ≥ 0,	തുടർച്ചയായി നടക്കുന്നു
		1-ന് x< 0
മുഴുവൻ നമ്പർ ലൈൻ. ഈ ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിക്കുക.
5.176 പ്രവർത്തനം തെളിയിക്കുക	f(x) = x2	1 x ≥ 0,	തുടർച്ചയായി അല്ല
		x-ൽ 0< 0

x = 0 എന്ന ബിന്ദുവിൽ, എന്നാൽ ആ ബിന്ദുവിൽ ശരിയായ തുടർച്ചയായി. f(x) ഫംഗ്‌ഷൻ ഗ്രാഫ് ചെയ്യുക.

x = പോയിന്റിലെ ഞെട്ടൽ

എന്നാൽ ഈ ഘട്ടത്തിൽ ഇടതുവശത്ത് തുടർച്ചയായി നിൽക്കുന്നു. ഒരു ഗ്രാഫ് നിർമ്മിക്കുക

ഫംഗ്ഷനുകൾ f(x).

5.178 ഗ്രാഫ് പ്രവർത്തനങ്ങൾ

a) y =

x+1

b) y= x+

x+1

x+1

x+1

ഈ ഫംഗ്‌ഷനുകളുടെ ബ്രേക്ക്‌പോയിന്റുകളിലെ തുടർച്ച വ്യവസ്ഥകളിൽ ഏതാണ് തൃപ്തികരവും തൃപ്തികരമല്ലാത്തതും?

5.179 ഫംഗ്ഷന്റെ ബ്രേക്ക് പോയിന്റ് വ്യക്തമാക്കുക

പാപം x		x ≠ 0 ന്
		x = 0-ൽ

ഈ ഘട്ടത്തിൽ ഏത് തുടർച്ച വ്യവസ്ഥകളാണ് തൃപ്തികരവും പാലിക്കാത്തതും?

നിർവ്വചനം ഫംഗ്ഷൻ ബ്രേക്ക് പോയിന്റുകൾ അവയുടെ തരങ്ങൾ പ്രവർത്തനത്തിന്റെ തുടർച്ചയുടെ പ്രമേയത്തിന്റെ തുടർച്ചയാണ്. ഒരു ഫംഗ്‌ഷന്റെ ബ്രേക്ക് പോയിന്റുകളുടെ അർത്ഥത്തിന്റെ വിഷ്വൽ (ഗ്രാഫിക്കൽ) വിശദീകരണവും തുടർച്ച എന്ന ആശയത്തിൽ നിന്ന് വ്യത്യസ്തമായി നൽകിയിരിക്കുന്നു. ഒരു ഫംഗ്‌ഷന്റെ ബ്രേക്ക്‌പോയിന്റുകൾ എങ്ങനെ കണ്ടെത്താമെന്നും അവയുടെ തരങ്ങൾ എങ്ങനെ നിർണ്ണയിക്കാമെന്നും നമുക്ക് പഠിക്കാം. ഞങ്ങളുടേത് ഇതിന് ഞങ്ങളെ സഹായിക്കും വിശ്വസ്തരായ സുഹൃത്തുക്കൾ- ഇടത്, വലത് പരിധികൾ, പൊതുവെ ഏകപക്ഷീയമായ പരിധികൾ എന്ന് വിളിക്കുന്നു. ഏകപക്ഷീയമായ പരിമിതികളെക്കുറിച്ച് ആർക്കെങ്കിലും ഭയമുണ്ടെങ്കിൽ, ഞങ്ങൾ അത് ഉടൻ ഇല്ലാതാക്കും.

പരസ്പരം ബന്ധിപ്പിച്ചിട്ടില്ലാത്ത ഒരു ഗ്രാഫിലെ പോയിന്റുകളെ വിളിക്കുന്നു ഫംഗ്ഷൻ ബ്രേക്ക് പോയിന്റുകൾ . ചുവടെയുള്ള ചിത്രത്തിൽ x=2 - - എന്ന ബിന്ദുവിൽ ഒരു വിരാമം നേരിടുന്ന അത്തരം ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫ്.

മേൽപ്പറഞ്ഞവയുടെ സാമാന്യവൽക്കരണം ഇനിപ്പറയുന്ന നിർവചനമാണ്. ഒരു ഫംഗ്‌ഷൻ ഒരു ബിന്ദുവിൽ തുടർച്ചയായി ഇല്ലെങ്കിൽ, ഈ ബിന്ദുവിൽ അതിന് ഒരു വിച്ഛേദം ഉണ്ടായിരിക്കും, ആ പോയിന്റിനെ തന്നെ വിളിക്കുന്നു. ബ്രേക്ക് പോയിന്റ് . തടസ്സങ്ങൾ ആദ്യ തരത്തിലും രണ്ടാമത്തെ തരത്തിലുമാണ് .

നിർണ്ണയിക്കാൻ വേണ്ടി ബ്രേക്ക് പോയിന്റുകളുടെ തരങ്ങൾ (പ്രതീകം). പ്രവർത്തനങ്ങൾ ആത്മവിശ്വാസത്തോടെ കണ്ടെത്തേണ്ടതുണ്ട് പരിധികൾ, അതിനാൽ അനുബന്ധ പാഠം ഒരു പുതിയ വിൻഡോയിൽ തുറക്കുന്നത് നല്ലതാണ്. എന്നാൽ ബ്രേക്ക്‌പോയിന്റുകളുമായി ബന്ധപ്പെട്ട്, ഞങ്ങൾക്ക് പുതിയതും പ്രധാനപ്പെട്ടതുമായ ചിലത് ഉണ്ട് - ഏകപക്ഷീയമായ (ഇടത്തും വലത്തും) പരിധികൾ. പൊതുവേ, അവ എഴുതപ്പെട്ടിരിക്കുന്നു (വലത് പരിധി), (ഇടത് പരിധി). പൊതുവായി ഒരു പരിധിയുടെ കാര്യത്തിലെന്നപോലെ, ഒരു ഫംഗ്‌ഷന്റെ പരിധി കണ്ടെത്തുന്നതിന്, നിങ്ങൾ X പ്രവണതയ്‌ക്കായി ഫംഗ്‌ഷന്റെ എക്‌സ്‌പ്രഷനിൽ X മാറ്റിസ്ഥാപിക്കേണ്ടതുണ്ട്. പക്ഷേ, ഒരുപക്ഷേ, നിങ്ങൾ ചോദിക്കുന്നു, വലത്, ഇടത് പരിധികൾ എങ്ങനെ വ്യത്യാസപ്പെടും, വലത് ഒന്നിന്റെ കാര്യത്തിൽ X-ലേക്ക് എന്തെങ്കിലും ചേർത്തിട്ടുണ്ടെങ്കിൽ, എന്നാൽ ഇത് എന്തെങ്കിലും പൂജ്യമാണ്, ഇടതുവശത്ത് X-ൽ നിന്ന് എന്തെങ്കിലും കുറയ്ക്കുകയാണെങ്കിൽ, എന്നാൽ ഇത് എന്തെങ്കിലും - പൂജ്യവും? നിങ്ങൾ ശരിയാകും. മിക്കവാറും സന്ദർഭങ്ങളിൽ.

എന്നാൽ ഒരു ഫംഗ്‌ഷന്റെ ഡിസ്‌കോൺറ്റിന്യൂറ്റി പോയിന്റുകൾക്കായി തിരയുകയും അവയുടെ തരം നിർണ്ണയിക്കുകയും ചെയ്യുന്ന സമ്പ്രദായത്തിൽ, വലത്, ഇടത് പരിധികൾ തുല്യമല്ലാത്ത രണ്ട് സാധാരണ കേസുകളുണ്ട്:

• ഒരു ഫംഗ്‌ഷനിൽ x ഉൾപ്പെടുന്ന സംഖ്യാരേഖയുടെ ഭാഗത്തെ ആശ്രയിച്ച് രണ്ടോ അതിലധികമോ പദപ്രയോഗങ്ങളുണ്ട് (ഈ പദപ്രയോഗങ്ങൾ സാധാരണയായി ചുരുണ്ട ബ്രാക്കറ്റുകളിൽ എഴുതുന്നു എഫ്(x)= );
• X പ്രവണതയെ മാറ്റിസ്ഥാപിക്കുന്നതിന്റെ ഫലമായി, ഛേദത്തിൽ നമുക്ക് ഒരു ഭിന്നസംഖ്യ ലഭിക്കുന്നു, അത് പ്ലസ് പൂജ്യം (+0) അല്ലെങ്കിൽ മൈനസ് പൂജ്യം (-0) ആയി തുടരും, അതിനാൽ അത്തരമൊരു ഭിന്നസംഖ്യ ഒന്നുകിൽ അനന്തത അല്ലെങ്കിൽ മൈനസ് അനന്തത എന്നാണ് അർത്ഥമാക്കുന്നത്, ഇവയാണ് തികച്ചും വ്യത്യസ്തമായ കാര്യങ്ങൾ.

ആദ്യ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റുകൾ

ആദ്യ തരത്തിലുള്ള ബ്രേക്ക് പോയിന്റ്: ഒരു ഫംഗ്‌ഷന് പരിമിതമായ (അതായത്, അനന്തതയ്‌ക്ക് തുല്യമല്ല) ഇടത് പരിധിയും പരിമിതമായ വലത് പരിധിയും ഉണ്ട്, എന്നാൽ ഫംഗ്‌ഷൻ ഒരു പോയിന്റിൽ നിർവചിച്ചിട്ടില്ല അല്ലെങ്കിൽ ഇടത്, വലത് പരിധികൾ വ്യത്യസ്തമാണ് (തുല്യമല്ല).

ആദ്യത്തെ തരത്തിലുള്ള നീക്കം ചെയ്യാവുന്ന നിർത്തലാക്കൽ പോയിന്റ്.ഇടത്, വലത് പരിധികൾ തുല്യമാണ്. ഈ സാഹചര്യത്തിൽ, ഒരു ഘട്ടത്തിൽ ഫംഗ്ഷൻ കൂടുതൽ നിർവചിക്കുന്നത് സാധ്യമാണ്. ഒരു പോയിന്റിൽ ഒരു ഫംഗ്ഷൻ നിർവചിക്കുക, ലളിതമായി പറഞ്ഞാൽ, ഇടത്, വലത് പരിധികൾ പരസ്പരം തുല്യമായി കാണപ്പെടുന്ന ഒരു പോയിന്റ് തമ്മിലുള്ള ഒരു കണക്ഷൻ നൽകുക എന്നാണ് അർത്ഥമാക്കുന്നത്. ഈ സാഹചര്യത്തിൽ, ഫംഗ്‌ഷന്റെ മൂല്യം കണ്ടെത്തേണ്ട ഒരു പോയിന്റ് മാത്രമേ കണക്ഷൻ പ്രതിനിധീകരിക്കാവൂ.

ഉദാഹരണം 1.ഫംഗ്ഷന്റെ ബ്രേക്ക് പോയിന്റും ബ്രേക്ക് പോയിന്റിന്റെ തരവും (പ്രതീകം) നിർണ്ണയിക്കുക.

രണ്ടാമത്തെ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റുകൾ

രണ്ടാമത്തെ തരത്തിലുള്ള ബ്രേക്ക് പോയിന്റ്: പരിധികളിൽ ഒരെണ്ണമെങ്കിലും (ഇടത് അല്ലെങ്കിൽ വലത്) അനന്തമായ പോയിന്റ് (അനന്തത്തിന് തുല്യമാണ്).

ഉദാഹരണം 3.

പരിഹാരം. പവർ എന്ന പദപ്രയോഗത്തിൽ നിന്ന് ഇപോയിന്റിൽ ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ലെന്ന് വ്യക്തമാണ്. ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെ ഇടത്, വലത് പരിധികൾ നമുക്ക് കണ്ടെത്താം:

പരിധികളിൽ ഒന്ന് അനന്തതയ്ക്ക് തുല്യമാണ്, അതിനാൽ പോയിന്റ് രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമ പോയിന്റാണ്. ബ്രേക്ക് പോയിന്റുള്ള ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫ് ഉദാഹരണത്തിനു താഴെയാണ്.

ഒരു ഫംഗ്‌ഷന്റെ ബ്രേക്ക്‌പോയിന്റുകൾ കണ്ടെത്തുന്നത് ഒന്നുകിൽ ഒരു സ്വതന്ത്ര ചുമതലയോ ഭാഗമോ ആകാം പൂർണ്ണ പ്രവർത്തന ഗവേഷണവും ഗ്രാഫിംഗും .

ഉദാഹരണം 4.ഫംഗ്ഷന്റെ ബ്രേക്ക് പോയിന്റും ഫംഗ്ഷന്റെ ബ്രേക്ക് പോയിന്റിന്റെ തരവും (പ്രതീകവും) നിർണ്ണയിക്കുക

പരിഹാരം. 2 ലെ ശക്തിയുടെ പദപ്രയോഗത്തിൽ നിന്ന്, പോയിന്റിൽ ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ലെന്ന് വ്യക്തമാണ്. ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെ ഇടത് വലത് പരിധികൾ കണ്ടെത്താം.

നീക്കം ചെയ്യാവുന്ന വിടവ്.

നിർവ്വചനം. ഡോട്ട് എഫംഗ്‌ഷന്റെ നീക്കം ചെയ്യാവുന്ന വിച്ഛേദിക്കുന്ന പോയിന്റ് എന്ന് വിളിക്കുന്നു y=f(x), ഫംഗ്ഷന്റെ പരിധി എങ്കിൽ f(x)ഈ ഘട്ടത്തിൽ നിലവിലുണ്ട്, പക്ഷേ പോയിന്റിൽ എപ്രവർത്തനം f(x)ഒന്നുകിൽ നിർവചിച്ചിട്ടില്ല അല്ലെങ്കിൽ ഒരു സ്വകാര്യ അർത്ഥമുണ്ട് f(a), പരിധിയിൽ നിന്ന് വ്യത്യസ്തമാണ് f(x)ഈ സമയത്ത്.

ഉദാഹരണം. ഉദാഹരണത്തിന്, പ്രവർത്തനം

പോയിന്റിൽ ഉണ്ട് x=0നന്നാക്കാവുന്ന വിടവ്. തീർച്ചയായും, പോയിന്റിലെ ഈ ഫംഗ്‌ഷന്റെ പരിമിതപ്പെടുത്തുന്ന മൂല്യം x=0 1 ന് തുല്യമാണ്. ഭാഗിക മൂല്യം 2 ന് തുല്യമാണ്.

ഫംഗ്ഷൻ എങ്കിൽ f(x)പോയിന്റിൽ ഉണ്ട് എനീക്കം ചെയ്യാവുന്ന വിടവ്, അല്ലാതെ മറ്റ് പോയിന്റുകളിൽ ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ മാറ്റാതെ തന്നെ ഈ വിടവ് ഇല്ലാതാക്കാൻ കഴിയും എ. ഇത് ചെയ്യുന്നതിന്, ഫംഗ്ഷന്റെ മൂല്യം പോയിന്റിൽ വെച്ചാൽ മതി എഈ ഘട്ടത്തിൽ അതിന്റെ പരിധി മൂല്യത്തിന് തുല്യമാണ്. അതിനാൽ, മുകളിൽ പരിഗണിച്ച ഉദാഹരണത്തിൽ ഇത് ഇട്ടാൽ മതി f(0)=1തുടർന്ന് , അതായത്. പ്രവർത്തനം f(x)പോയിന്റിൽ തുടർച്ചയായി മാറും x=0.

ആദ്യ തരത്തിലുള്ള തടസ്സം.

നിർവ്വചനം. ഡോട്ട് എഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷൻ ആണെങ്കിൽ, ആദ്യത്തെ തരത്തിലുള്ള ഡിസ്‌കണ്ടിന്യുറ്റി പോയിന്റ് എന്ന് വിളിക്കുന്നു f(x)പരിമിതവും എന്നാൽ അസമവുമായ വലത് ഇടത് പരിധികളുണ്ട്

ചില ഉദാഹരണങ്ങൾ പറയാം.

ഉദാഹരണം. ഫംഗ്ഷൻ y=sgn xപോയിന്റിൽ ഉണ്ട് x=0ആദ്യത്തെ തരത്തിലുള്ള വിള്ളൽ. തീർച്ചയായും, അതിനാൽ ഈ പരിധികൾ പരസ്പരം തുല്യമല്ല.

ഉദാഹരണം. ഫംഗ്ഷൻ , പോയിന്റ് ഒഴികെ എല്ലായിടത്തും നിർവചിച്ചിരിക്കുന്നു x=1, പോയിന്റിൽ ഉണ്ട് x=1ആദ്യത്തെ തരത്തിലുള്ള വിള്ളൽ. തീർച്ചയായും, .

രണ്ടാമത്തെ തരത്തിലുള്ള തടസ്സം.

നിർവ്വചനം. ഡോട്ട് എഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷൻ ആണെങ്കിൽ രണ്ടാമത്തെ തരത്തിലുള്ള ഡിസ്‌കണ്ടിന്യുറ്റി പോയിന്റ് എന്ന് വിളിക്കുന്നു f(x)ഏകപക്ഷീയമായ പരിമിതികളിൽ ഒരെണ്ണമെങ്കിലും ഇല്ല അല്ലെങ്കിൽ ഏകപക്ഷീയമായ പരിധികളിൽ ഒരെണ്ണമെങ്കിലും അനന്തമാണെങ്കിൽ.

ഉദാഹരണം. ഫംഗ്ഷൻ f(x)=ടാൻ x, വ്യക്തമായും, ഓരോ പോയിന്റിലും രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമം ഉണ്ട് x k =π/2+π k, k=0, ± 1, ± 2,..., കാരണം അത്തരം ഓരോ ഘട്ടത്തിലും

ഉദാഹരണം. പ്രവർത്തനത്തിന് പോയിന്റിൽ രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമം ഉണ്ട് x=0, കാരണം ഈ ഘട്ടത്തിൽ അതിന് വലത് അല്ലെങ്കിൽ ഇടത് പരിധികളില്ല.

ഒരു സെഗ്‌മെന്റിൽ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച

നിർവ്വചനം. ഒരു ഇടവേളയിൽ നിർവ്വചിച്ച പ്രവർത്തനം അതിന്റെ ഓരോ പോയിന്റിലും തുടർച്ചയായി ഈ സെഗ്മെന്റിൽ തുടർച്ചയായി വിളിക്കുന്നു.

മാത്രമല്ല, പോയിന്റിൽ തുടർച്ചയായി കീഴിൽ എവലതുവശത്ത് തുടർച്ചയായും ഒരു ബിന്ദുവിലെ തുടർച്ചയായും മനസ്സിലാക്കുന്നു ബി- ഇടതുവശത്ത് തുടർച്ച.

ഞങ്ങൾ ഫംഗ്ഷൻ എന്ന് പറയും y=f(x), സെറ്റിൽ നിർവചിച്ചിരിക്കുന്നു (x)അതിന്റെ മുകളിലെ (താഴത്തെ) അറ്റത്ത് എത്തുന്നു , അത്തരമൊരു പോയിന്റ് നിലവിലുണ്ടെങ്കിൽ x 0 ∈(x), എന്ത് f(x 0)=β (f(x 0)=α).

[വീർസ്ട്രാസ്] സിദ്ധാന്തം. ഒരു ഇടവേളയിൽ തുടർച്ചയായി നടക്കുന്ന എല്ലാ പ്രവർത്തനങ്ങളും പരിമിതപ്പെടുത്തുകയും അതിന്റെ മുകളിലെ പരിധിയിലും അതിന്റെ താഴത്തെ പരിധിയിലും എത്തുകയും ചെയ്യുന്നു.

സിദ്ധാന്തം [Bolzano-Cauchy]. ഫംഗ്ഷൻ എങ്കിൽ y=f(x)സെഗ്മെന്റിൽ തുടർച്ചയായി ഒപ്പം f(a)=A, f(b)=B, പിന്നെ ഏതിനും സി, ഇടയിൽ ഉപസംഹരിച്ചു എഒപ്പം ബി, അങ്ങനെയൊരു പോയിന്റുണ്ട് ξ∈ , എന്ത് f(ξ)=C.

മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ഏതെങ്കിലും രണ്ട് മൂല്യങ്ങൾ എടുക്കുന്ന ഒരു ഇടവേളയിൽ തുടർച്ചയായ ഒരു ഫംഗ്ഷൻ അവയ്ക്കിടയിൽ കിടക്കുന്ന ഏത് മൂല്യവും എടുക്കുന്നു.

അനന്തരഫലം. ഒരു ഫംഗ്‌ഷൻ ഒരു സെഗ്‌മെന്റിൽ തുടർച്ചയായിരിക്കുകയും അതിന്റെ അറ്റത്ത് വിവിധ ചിഹ്നങ്ങളുടെ മൂല്യങ്ങൾ എടുക്കുകയും ചെയ്യുന്നുവെങ്കിൽ, ഈ സെഗ്‌മെന്റിൽ ഫംഗ്‌ഷൻ അപ്രത്യക്ഷമാകുന്ന ഒരു പോയിന്റെങ്കിലും ഉണ്ടായിരിക്കും.

അനന്തരഫലം. പ്രവർത്തനം നടക്കട്ടെ y=f(x)സെഗ്മെന്റിൽ തുടർച്ചയായി ഒപ്പം , . തുടർന്ന് ചടങ്ങ് f(x)സെഗ്മെന്റിൽ നിന്ന് എല്ലാ മൂല്യങ്ങളും എടുക്കുന്നു ഈ മൂല്യങ്ങൾ മാത്രം.

അങ്ങനെ, ഒരു നിശ്ചിത സെഗ്‌മെന്റിൽ നൽകിയിരിക്കുന്നതും തുടർച്ചയായതുമായ ഒരു ഫംഗ്‌ഷന്റെ എല്ലാ മൂല്യങ്ങളുടെയും ഗണവും ഒരു സെഗ്‌മെന്റാണ്.

പ്രവർത്തനത്തിന്റെ തുടർച്ച. ബ്രേക്കിംഗ് പോയിന്റുകൾ.

കാള നടക്കുന്നു, ആടുന്നു, നെടുവീർപ്പിടുന്നു:
- ഓ, ബോർഡ് തീർന്നു, ഇപ്പോൾ ഞാൻ വീഴാൻ പോകുന്നു!

ഈ പാഠത്തിൽ ഒരു ഫംഗ്ഷന്റെ തുടർച്ച എന്ന ആശയം, നിർത്തലാക്കൽ പോയിന്റുകളുടെ വർഗ്ഗീകരണം, ഒരു പൊതു പ്രായോഗിക പ്രശ്നം എന്നിവ ഞങ്ങൾ പരിശോധിക്കും. പ്രവർത്തനങ്ങളുടെ തുടർച്ചയായ പഠനം. വിഷയത്തിന്റെ പേരിൽ നിന്ന്, എന്താണ് ചർച്ച ചെയ്യപ്പെടേണ്ടതെന്ന് പലരും അവബോധപൂർവ്വം ഊഹിക്കുകയും മെറ്റീരിയൽ വളരെ ലളിതമാണെന്ന് കരുതുകയും ചെയ്യുന്നു. ഇത് സത്യമാണ്. എന്നാൽ അവഗണനയ്ക്കും അവ പരിഹരിക്കുന്നതിനുള്ള ഉപരിപ്ലവമായ സമീപനത്തിനും മിക്കപ്പോഴും ശിക്ഷിക്കപ്പെടുന്നത് ലളിതമായ ജോലികളാണ്. അതിനാൽ, നിങ്ങൾ ലേഖനം വളരെ ശ്രദ്ധാപൂർവ്വം പഠിക്കാനും എല്ലാ സൂക്ഷ്മതകളും സാങ്കേതികതകളും പിടിക്കാനും ഞാൻ ശുപാർശ ചെയ്യുന്നു.

നിങ്ങൾക്ക് എന്താണ് അറിയേണ്ടതും ചെയ്യാൻ കഴിയേണ്ടതും?വളരെ അല്ല. പാഠം നന്നായി പഠിക്കാൻ, അത് എന്താണെന്ന് നിങ്ങൾ മനസ്സിലാക്കേണ്ടതുണ്ട് ഒരു ഫംഗ്‌ഷന്റെ പരിധി. കൂടെ വായനക്കാർ താഴ്ന്ന നിലലേഖനം മനസ്സിലാക്കാൻ തയ്യാറെടുപ്പ് മതി പ്രവർത്തന പരിധികൾ. പരിഹാരങ്ങളുടെ ഉദാഹരണങ്ങൾനോക്കാനും ജ്യാമിതീയ അർത്ഥംമാനുവലിൽ പരിധി പ്രാഥമിക പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകളും ഗുണങ്ങളും. സ്വയം പരിചയപ്പെടുത്തുന്നതും ഉചിതമാണ് ഗ്രാഫുകളുടെ ജ്യാമിതീയ രൂപാന്തരങ്ങൾ, മിക്ക കേസുകളിലും പരിശീലനത്തിൽ ഒരു ഡ്രോയിംഗ് നിർമ്മിക്കുന്നത് ഉൾപ്പെടുന്നു. സാധ്യതകൾ എല്ലാവർക്കും ശുഭാപ്തിവിശ്വാസമാണ്, അടുത്ത ഒന്നോ രണ്ടോ മണിക്കൂറിനുള്ളിൽ ഒരു പൂർണ്ണ കെറ്റിലിന് പോലും ചുമതലയെ നേരിടാൻ കഴിയും!

പ്രവർത്തനത്തിന്റെ തുടർച്ച. ബ്രേക്ക് പോയിന്റുകളും അവയുടെ വർഗ്ഗീകരണവും

പ്രവർത്തനത്തിന്റെ തുടർച്ച എന്ന ആശയം

മുഴുവൻ സംഖ്യാരേഖയിലും തുടർച്ചയായി തുടരുന്ന ചില ഫംഗ്‌ഷൻ നമുക്ക് പരിഗണിക്കാം:

അല്ലെങ്കിൽ, കൂടുതൽ സംക്ഷിപ്തമായി പറഞ്ഞാൽ, ഞങ്ങളുടെ പ്രവർത്തനം (യഥാർത്ഥ സംഖ്യകളുടെ സെറ്റ്) ഓൺ ആണ്.

തുടർച്ചയുടെ "ഫിലിസ്ത്യൻ" മാനദണ്ഡം എന്താണ്? വ്യക്തമായും ഷെഡ്യൂൾ തുടർച്ചയായ പ്രവർത്തനംപേപ്പറിൽ നിന്ന് പെൻസിൽ ഉയർത്താതെ തന്നെ വരയ്ക്കാം.

ഈ സാഹചര്യത്തിൽ, രണ്ട് ലളിതമായ ആശയങ്ങൾ വ്യക്തമായി വേർതിരിച്ചറിയണം: ഒരു ഫംഗ്ഷന്റെ ഡൊമെയ്ൻഒപ്പം പ്രവർത്തനത്തിന്റെ തുടർച്ച. IN പൊതുവായ കേസ് അത് ഒരേ കാര്യമല്ല. ഉദാഹരണത്തിന്:

ഈ ഫംഗ്ഷൻ മുഴുവൻ നമ്പർ ലൈനിലും നിർവചിച്ചിരിക്കുന്നു, അതായത് എല്ലാവരും"x" എന്നതിന്റെ അർത്ഥത്തിന് "y" എന്നതിന് അതിന്റേതായ അർത്ഥമുണ്ട്. പ്രത്യേകിച്ചും, എങ്കിൽ . മറ്റൊരു പോയിന്റ് വിരാമചിഹ്നമാണെന്ന് ശ്രദ്ധിക്കുക, കാരണം ഒരു ഫംഗ്ഷന്റെ നിർവചനം അനുസരിച്ച്, ആർഗ്യുമെന്റിന്റെ മൂല്യം ഇതുമായി പൊരുത്തപ്പെടണം ഒരേ ഒരു കാര്യംപ്രവർത്തന മൂല്യം. അങ്ങനെ, ഡൊമെയ്ൻഞങ്ങളുടെ പ്രവർത്തനം: .

എന്നിരുന്നാലും ഈ ഫംഗ്ഷൻ തുടർച്ചയായി അല്ല!ആ ഘട്ടത്തിൽ അവൾ കഷ്ടപ്പെടുന്നു എന്നത് വളരെ വ്യക്തമാണ് വിടവ്. ഈ പദം വളരെ മനസ്സിലാക്കാവുന്നതും ദൃശ്യപരവുമാണ്; തീർച്ചയായും, ഇവിടെ പെൻസിൽ എന്തായാലും പേപ്പറിൽ നിന്ന് കീറേണ്ടി വരും. കുറച്ച് കഴിഞ്ഞ് നമ്മൾ ബ്രേക്ക്പോയിന്റുകളുടെ വർഗ്ഗീകരണം നോക്കും.

ഒരു ഘട്ടത്തിലും ഇടവേളയിലും ഒരു ഫംഗ്ഷന്റെ തുടർച്ച

ഒരു പ്രത്യേക ഗണിത പ്രശ്‌നത്തിൽ, ഒരു ഘട്ടത്തിലെ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച, ഒരു ഇടവേളയിലെ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച, ഒരു പകുതി-ഇന്റർവെൽ അല്ലെങ്കിൽ ഒരു സെഗ്‌മെന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ച എന്നിവയെക്കുറിച്ച് നമുക്ക് സംസാരിക്കാം. അതാണ്, "വെറും തുടർച്ച" ഇല്ല- പ്രവർത്തനം എവിടെയെങ്കിലും തുടർച്ചയായി തുടരാം. മറ്റെല്ലാറ്റിന്റെയും അടിസ്ഥാന "ബിൽഡിംഗ് ബ്ലോക്ക്" ആണ് പ്രവർത്തനത്തിന്റെ തുടർച്ച പോയിന്റിൽ .

സിദ്ധാന്തം ഗണിത വിശകലനം"ഡെൽറ്റ", "എപ്സിലോൺ" എന്നീ അയൽപക്കങ്ങൾ ഉപയോഗിച്ച് ഒരു ഘട്ടത്തിൽ ഒരു ഫംഗ്ഷന്റെ തുടർച്ചയുടെ ഒരു നിർവചനം നൽകുന്നു, എന്നാൽ പ്രായോഗികമായി മറ്റൊരു നിർവചനം ഉപയോഗത്തിലുണ്ട്, അത് ഞങ്ങൾ ശ്രദ്ധയോടെ ശ്രദ്ധിക്കും.

ആദ്യം നമുക്ക് ഓർക്കാം ഏകപക്ഷീയമായ പരിധികൾആദ്യ പാഠത്തിൽ നമ്മുടെ ജീവിതത്തിലേക്ക് പൊട്ടിത്തെറിച്ചവർ ഫംഗ്ഷൻ ഗ്രാഫുകളെ കുറിച്ച്. ദൈനംദിന സാഹചര്യം പരിഗണിക്കുക:

നമ്മൾ അച്ചുതണ്ടിനെ പോയിന്റിലേക്ക് സമീപിക്കുകയാണെങ്കിൽ ഇടത്തെ(ചുവന്ന അമ്പടയാളം), തുടർന്ന് “ഗെയിമുകളുടെ” അനുബന്ധ മൂല്യങ്ങൾ അച്ചുതണ്ടിലൂടെ പോയിന്റിലേക്ക് (ക്രിംസൺ അമ്പടയാളം) പോകും. ഗണിതശാസ്ത്രപരമായി, ഈ വസ്തുത ഉപയോഗിച്ച് ഉറപ്പിച്ചിരിക്കുന്നു ഇടത് കൈ പരിധി:

എൻട്രിയിൽ ശ്രദ്ധിക്കുക ("എക്സ് ഇടത് വശത്ത് ka എന്ന് വായിക്കുന്നു"). "അഡിറ്റീവ്" "മൈനസ് പൂജ്യം" പ്രതീകപ്പെടുത്തുന്നു , അടിസ്ഥാനപരമായി ഇതിനർത്ഥം ഞങ്ങൾ ഇടത് വശത്ത് നിന്ന് നമ്പറിലേക്ക് അടുക്കുന്നു എന്നാണ്.

അതുപോലെ, നിങ്ങൾ "ക" എന്ന പോയിന്റിനെ സമീപിക്കുകയാണെങ്കിൽ വലതുവശത്ത്(നീല അമ്പടയാളം), തുടർന്ന് "ഗെയിമുകൾ" അതേ മൂല്യത്തിലേക്ക് വരും, പക്ഷേ പച്ച അമ്പടയാളത്തിനൊപ്പം, ഒപ്പം വലതുവശത്തെ പരിധിഇനിപ്പറയുന്ന രീതിയിൽ ഫോർമാറ്റ് ചെയ്യും:

"അഡിറ്റീവ്" പ്രതീകപ്പെടുത്തുന്നു , കൂടാതെ എൻട്രി ഇങ്ങനെ വായിക്കുന്നു: "x വലതുവശത്ത് ka ആയി മാറുന്നു."

ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും തുല്യവുമാണെങ്കിൽ(ഞങ്ങളുടെ കാര്യത്തിലെന്നപോലെ): , അപ്പോൾ നമ്മൾ പറയും ഒരു GENERAL പരിധി ഉണ്ടെന്ന്. ഇത് ലളിതമാണ്, പൊതുവായ പരിധി ഞങ്ങളുടെ "സാധാരണ" ആണ് ഒരു ഫംഗ്‌ഷന്റെ പരിധി, ഒരു പരിമിത സംഖ്യയ്ക്ക് തുല്യം.

ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ലെങ്കിൽ (പഞ്ചർ കറുത്ത ഡോട്ട്ഗ്രാഫ് ബ്രാഞ്ചിൽ), മുകളിൽ പറഞ്ഞ കണക്കുകൂട്ടലുകൾ സാധുവായി തുടരും. ഇതിനകം പലതവണ സൂചിപ്പിച്ചതുപോലെ, പ്രത്യേകിച്ച് ലേഖനത്തിൽ അനന്തമായ പ്രവർത്തനങ്ങളിൽ, പദപ്രയോഗങ്ങൾ അർത്ഥമാക്കുന്നത് "x" എന്നാണ്. അനന്തമായി അടുത്ത്പോയിന്റിനെ സമീപിക്കുന്നു, അതേസമയം കാര്യമില്ല, ഫംഗ്ഷൻ തന്നെ ഒരു നിശ്ചിത പോയിന്റിൽ നിർവചിച്ചിട്ടുണ്ടോ ഇല്ലയോ എന്ന്. നല്ല ഉദാഹരണംഫംഗ്ഷൻ വിശകലനം ചെയ്യുമ്പോൾ അടുത്ത ഖണ്ഡികയിൽ ദൃശ്യമാകും.

നിർവ്വചനം: ഒരു നിശ്ചിത പോയിന്റിലെ ഫംഗ്‌ഷന്റെ പരിധി ആ പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യത്തിന് തുല്യമാണെങ്കിൽ ഒരു ഫംഗ്‌ഷൻ ഒരു ബിന്ദുവിൽ തുടർച്ചയായിരിക്കും: .

നിർവചനം വിശദമായി വിവരിച്ചിരിക്കുന്നു ഇനിപ്പറയുന്ന വ്യവസ്ഥകൾ:

1) ഫംഗ്ഷൻ പോയിന്റിൽ നിർവചിച്ചിരിക്കണം, അതായത് മൂല്യം നിലനിൽക്കണം.

2) പ്രവർത്തനത്തിന് പൊതുവായ ഒരു പരിധി ഉണ്ടായിരിക്കണം. മുകളിൽ സൂചിപ്പിച്ചതുപോലെ, ഇത് ഏകപക്ഷീയമായ പരിധികളുടെ അസ്തിത്വവും സമത്വവും സൂചിപ്പിക്കുന്നു: .

3) ഒരു നിശ്ചിത പോയിന്റിലെ ഫംഗ്‌ഷന്റെ പരിധി ഈ പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യത്തിന് തുല്യമായിരിക്കണം: .

ലംഘിച്ചാൽ ഒരെണ്ണമെങ്കിലുംമൂന്ന് വ്യവസ്ഥകളിൽ, തുടർന്ന് പ്രവർത്തനത്തിന് പോയിന്റിലെ തുടർച്ചയുടെ സ്വത്ത് നഷ്ടപ്പെടും.

ഒരു ഇടവേളയിൽ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ചസമർത്ഥമായും വളരെ ലളിതമായും രൂപപ്പെടുത്തിയിരിക്കുന്നു: തന്നിരിക്കുന്ന ഇടവേളയുടെ ഓരോ ബിന്ദുവിലും ഒരു ഫംഗ്ഷൻ തുടർച്ചയായി ആണെങ്കിൽ ഇടവേളയിൽ തുടർച്ചയായി പ്രവർത്തിക്കുന്നു.

പ്രത്യേകിച്ചും, പല ഫംഗ്ഷനുകളും അനന്തമായ ഇടവേളയിൽ, അതായത് യഥാർത്ഥ സംഖ്യകളുടെ ഗണത്തിൽ തുടർച്ചയായി തുടരുന്നു. ഇതൊരു ലീനിയർ ഫംഗ്‌ഷൻ, പോളിനോമിയലുകൾ, എക്‌സ്‌പോണൻഷ്യൽ, സൈൻ, കോസൈൻ മുതലായവയാണ്. പൊതുവേ, ഏതെങ്കിലും പ്രാഥമിക പ്രവർത്തനംഅതിന്റെ തുടർച്ചയായി നിർവചനത്തിന്റെ ഡൊമെയ്ൻ, ഉദാഹരണത്തിന്, ഒരു ലോഗരിഥമിക് ഫംഗ്ഷൻ ഇടവേളയിൽ തുടർച്ചയായി പ്രവർത്തിക്കുന്നു. ഞാൻ പ്രതീക്ഷിക്കുന്നു ഈ നിമിഷംപ്രധാന പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകൾ എങ്ങനെയിരിക്കും എന്നതിനെക്കുറിച്ച് നിങ്ങൾക്ക് നല്ല ധാരണയുണ്ട്. കൂടുതൽ പൂർണമായ വിവരംഅവരുടെ തുടർച്ചയിൽ നിന്ന് ശേഖരിക്കാവുന്നതാണ് ദയയുള്ള വ്യക്തി Fichtengolts എന്ന കുടുംബപ്പേരിൽ.

ഒരു സെഗ്‌മെന്റിലും പകുതി ഇടവേളകളിലും ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ചയോടെ, എല്ലാം ബുദ്ധിമുട്ടുള്ള കാര്യമല്ല, പക്ഷേ ക്ലാസിൽ ഇതിനെക്കുറിച്ച് സംസാരിക്കുന്നത് കൂടുതൽ ഉചിതമാണ്. ഒരു സെഗ്‌മെന്റിൽ ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞതും കൂടിയതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിനെക്കുറിച്ച്, എന്നാൽ ഇപ്പോൾ അതിനെക്കുറിച്ച് വിഷമിക്കേണ്ടതില്ല.

ബ്രേക്ക് പോയിന്റുകളുടെ വർഗ്ഗീകരണം

ഫംഗ്ഷനുകളുടെ ആകർഷകമായ ജീവിതം എല്ലാത്തരം പ്രത്യേക പോയിന്റുകളാലും സമ്പന്നമാണ്, ബ്രേക്ക് പോയിന്റുകൾ അവരുടെ ജീവചരിത്രത്തിന്റെ പേജുകളിൽ ഒന്ന് മാത്രമാണ്.

കുറിപ്പ് : അങ്ങനെയെങ്കിൽ, ഞാൻ ഒരു പ്രാഥമിക പോയിന്റിൽ വസിക്കും: ബ്രേക്കിംഗ് പോയിന്റ് എപ്പോഴും ഒറ്റ പോയിന്റ്- "ഒരു നിരയിൽ നിരവധി ബ്രേക്ക് പോയിന്റുകൾ" ഇല്ല, അതായത്, "ബ്രേക്ക് ഇന്റർവെൽ" എന്നൊന്നില്ല.

ഈ പോയിന്റുകൾ രണ്ടായി തിരിച്ചിരിക്കുന്നു വലിയ ഗ്രൂപ്പുകൾ: ആദ്യ തരത്തിലുള്ള വിള്ളലുകൾഒപ്പം രണ്ടാമത്തെ തരത്തിലുള്ള വിള്ളലുകൾ. ഓരോ തരം വിടവിനും അതിന്റേതായ ഉണ്ട് സവിശേഷതകൾഞങ്ങൾ ഇപ്പോൾ നോക്കുന്നത്:

ആദ്യ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റ്

ഒരു ഘട്ടത്തിൽ തുടർച്ച വ്യവസ്ഥ ലംഘിച്ചാൽ ഏകപക്ഷീയമായ പരിധികളും പരിമിതമായ , അപ്പോൾ അത് വിളിക്കപ്പെടുന്നു ആദ്യ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റ്.

ഏറ്റവും ശുഭാപ്തി വിശ്വാസത്തോടെ നമുക്ക് ആരംഭിക്കാം. പാഠത്തിന്റെ യഥാർത്ഥ ആശയം അനുസരിച്ച്, "ഇൻ" എന്ന സിദ്ധാന്തം പറയാൻ ഞാൻ ആഗ്രഹിച്ചു പൊതുവായ കാഴ്ച”, എന്നാൽ മെറ്റീരിയലിന്റെ യാഥാർത്ഥ്യം പ്രകടിപ്പിക്കുന്നതിനായി, നിർദ്ദിഷ്ട പ്രതീകങ്ങളുള്ള ഓപ്ഷനിൽ ഞാൻ സ്ഥിരതാമസമാക്കി.

നിത്യജ്വാലയുടെ പശ്ചാത്തലത്തിൽ നവദമ്പതികളുടെ ഫോട്ടോ പോലെ ഇത് സങ്കടകരമാണ്, പക്ഷേ ഇനിപ്പറയുന്ന ഷോട്ട് പൊതുവെ അംഗീകരിക്കപ്പെടുന്നു. ഡ്രോയിംഗിലെ ഫംഗ്ഷന്റെ ഗ്രാഫ് നമുക്ക് ചിത്രീകരിക്കാം:


ഈ ഫംഗ്‌ഷൻ പോയിന്റ് ഒഴികെ മുഴുവൻ നമ്പർ ലൈനിലും തുടർച്ചയായി തുടരുന്നു. വാസ്തവത്തിൽ, ഡിനോമിനേറ്റർ പൂജ്യത്തിന് തുല്യമാകില്ല. എന്നിരുന്നാലും, പരിധിയുടെ അർത്ഥത്തിന് അനുസൃതമായി, നമുക്ക് കഴിയും അനന്തമായി അടുത്ത്ഇടത്തുനിന്നും വലത്തുനിന്നും "പൂജ്യം" എന്നതിനെ സമീപിക്കുക, അതായത്, ഏകപക്ഷീയമായ പരിധികൾ നിലവിലുണ്ട്, വ്യക്തമായും, യോജിക്കുന്നു:
(തുടർച്ചയുടെ വ്യവസ്ഥ നമ്പർ 2 തൃപ്തികരമാണ്).

എന്നാൽ ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ നിർവചിക്കപ്പെട്ടിട്ടില്ല, അതിനാൽ, തുടർച്ചയായി വ്യവസ്ഥ നമ്പർ.

ഇത്തരത്തിലുള്ള ഒരു ഇടവേള (നിലവിലുള്ളതിനൊപ്പം പൊതു പരിധി) വിളിക്കുന്നു നന്നാക്കാവുന്ന വിടവ്. എന്തുകൊണ്ടാണ് നീക്കം ചെയ്യാവുന്നത്? കാരണം പ്രവർത്തനത്തിന് കഴിയും പുനർ നിർവചിക്കുകബ്രേക്കിംഗ് പോയിന്റിൽ:

ഇത് വിചിത്രമായി തോന്നുന്നുണ്ടോ? ഒരുപക്ഷേ. എന്നാൽ അത്തരമൊരു ഫംഗ്ഷൻ നൊട്ടേഷൻ ഒന്നിനും വിരുദ്ധമല്ല! ഇപ്പോൾ വിടവ് അടഞ്ഞു, എല്ലാവരും സന്തോഷത്തിലാണ്:


നമുക്ക് ഒരു ഔപചാരിക പരിശോധന നടത്താം:

2) - ഒരു പൊതു പരിധി ഉണ്ട്;
3)

അങ്ങനെ, മൂന്ന് വ്യവസ്ഥകളും സംതൃപ്തമാണ്, ഒരു ഘട്ടത്തിൽ ഒരു ഫംഗ്ഷന്റെ തുടർച്ചയുടെ നിർവചനം അനുസരിച്ച് പ്രവർത്തനം ഒരു ഘട്ടത്തിൽ തുടർച്ചയായി തുടരുന്നു.

എന്നിരുന്നാലും, മാറ്റാൻ വെറുക്കുന്നവർക്ക് പ്രവർത്തനത്തെ മോശമായ രീതിയിൽ നിർവചിക്കാൻ കഴിയും, ഉദാഹരണത്തിന് :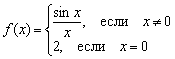


ആദ്യത്തെ രണ്ട് തുടർച്ച വ്യവസ്ഥകൾ ഇവിടെ തൃപ്തികരമാണ് എന്നത് രസകരമാണ്:
1) - ഫംഗ്ഷൻ ഒരു നിശ്ചിത പോയിന്റിൽ നിർവചിച്ചിരിക്കുന്നു;
2) - ഒരു പൊതു പരിധി ഉണ്ട്.

എന്നാൽ മൂന്നാമത്തെ അതിർത്തി കടന്നിട്ടില്ല: , അതായത്, പോയിന്റിലെ പ്രവർത്തനത്തിന്റെ പരിധി തുല്യമല്ലഒരു നിശ്ചിത പോയിന്റിൽ നൽകിയിരിക്കുന്ന ഫംഗ്ഷന്റെ മൂല്യം.

അങ്ങനെ, ഒരു ഘട്ടത്തിൽ പ്രവർത്തനം ഒരു വിരാമം നേരിടുന്നു.

രണ്ടാമത്തെ, സങ്കടകരമായ കേസ് വിളിക്കുന്നു ആദ്യത്തെ തരത്തിലുള്ള വിള്ളൽ ഒരു കുതിച്ചുചാട്ടത്തോടെ. ഏകപക്ഷീയമായ പരിമിതികളാൽ സങ്കടം ഉണർത്തപ്പെടുന്നു പരിമിതവും വ്യത്യസ്തവുമാണ്. പാഠത്തിന്റെ രണ്ടാമത്തെ ഡ്രോയിംഗിൽ ഒരു ഉദാഹരണം കാണിച്ചിരിക്കുന്നു. അത്തരമൊരു വിടവ് സാധാരണയായി സംഭവിക്കുന്നത് ഭാഗികമായി നിർവ്വചിച്ച പ്രവർത്തനങ്ങൾ, ലേഖനത്തിൽ ഇതിനകം പരാമർശിച്ചിട്ടുള്ളവ ഗ്രാഫ് പരിവർത്തനങ്ങളെക്കുറിച്ച്.

പീസ്വൈസ് ഫംഗ്ഷൻ പരിഗണിക്കുക ഞങ്ങൾ അതിന്റെ ഡ്രോയിംഗ് പൂർത്തിയാക്കും. ഒരു ഗ്രാഫ് എങ്ങനെ നിർമ്മിക്കാം? വളരെ ലളിതം. ഒരു പകുതി ഇടവേളയിൽ ഞങ്ങൾ ഒരു പരവലയത്തിന്റെ ഒരു ഭാഗം വരയ്ക്കുന്നു ( പച്ച നിറം), ഇടവേളയിൽ - ഒരു നേർരേഖ സെഗ്‌മെന്റ് (ചുവപ്പ്), പകുതി ഇടവേളയിൽ - ഒരു നേർരേഖ ( നീല നിറം).

മാത്രമല്ല, അസമത്വം കാരണം, മൂല്യം നിർണ്ണയിക്കപ്പെടുന്നു ചതുരാകൃതിയിലുള്ള പ്രവർത്തനം(പച്ച ഡോട്ട്), അസമത്വം കാരണം മൂല്യം നിർണ്ണയിക്കപ്പെടുന്നു രേഖീയ പ്രവർത്തനം(നീല ഡോട്ട്):

ഏറ്റവും പ്രയാസകരമായ സാഹചര്യത്തിൽ, നിങ്ങൾ ഗ്രാഫിന്റെ ഓരോ ഭാഗത്തിന്റെയും പോയിന്റ്-ബൈ-പോയിന്റ് നിർമ്മാണം അവലംബിക്കേണ്ടതാണ് (ആദ്യത്തേത് കാണുക പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകളെക്കുറിച്ചുള്ള പാഠം).

ഇപ്പോൾ നമുക്ക് പോയിന്റിൽ മാത്രമേ താൽപ്പര്യമുണ്ടാകൂ. തുടർച്ചയ്ക്കായി നമുക്ക് ഇത് പരിശോധിക്കാം:

2) നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കാം.

ഇടതുവശത്ത് നമുക്ക് ഒരു ചുവന്ന വര സെഗ്‌മെന്റ് ഉണ്ട്, അതിനാൽ ഇടത് വശത്തുള്ള പരിധി ഇതാണ്:

വലതുവശത്ത് നീല നേർരേഖയും വലതുവശത്തെ പരിധി:

തൽഫലമായി, ഞങ്ങൾക്ക് ലഭിച്ചു പരിമിത സംഖ്യകൾ, പിന്നെ അവർ തുല്യമല്ല. ഏകപക്ഷീയമായ പരിധി മുതൽ പരിമിതവും വ്യത്യസ്തവുമാണ്: , അപ്പോൾ ഞങ്ങളുടെ പ്രവർത്തനം സഹിക്കുന്നു ഒരു കുതിച്ചുചാട്ടത്തോടുകൂടിയ ആദ്യത്തെ തരത്തിലുള്ള നിർത്തലാക്കൽ.

വിടവ് ഇല്ലാതാക്കാൻ കഴിയില്ല എന്നത് യുക്തിസഹമാണ് - മുമ്പത്തെ ഉദാഹരണത്തിലെന്നപോലെ ഫംഗ്ഷൻ കൂടുതൽ നിർവചിക്കാനും “ഒരുമിച്ച് ഒട്ടിക്കാനും” കഴിയില്ല.

രണ്ടാമത്തെ തരത്തിലുള്ള വിച്ഛേദിക്കൽ പോയിന്റുകൾ

സാധാരണയായി, മറ്റെല്ലാ വിള്ളലുകളും ഈ വിഭാഗത്തിലേക്ക് സമർത്ഥമായി തരംതിരിച്ചിരിക്കുന്നു. ഞാൻ എല്ലാം ലിസ്റ്റുചെയ്യില്ല, കാരണം പ്രായോഗികമായി, 99% പ്രശ്നങ്ങളിൽ നിങ്ങൾ അഭിമുഖീകരിക്കും അനന്തമായ വിടവ്- ഇടംകൈയോ വലംകൈയോ ആയിരിക്കുമ്പോൾ, മിക്കപ്പോഴും, രണ്ട് പരിധികളും അനന്തമാണ്.

കൂടാതെ, തീർച്ചയായും, ഏറ്റവും വ്യക്തമായ ചിത്രം പൂജ്യത്തിലെ ഹൈപ്പർബോളയാണ്. ഇവിടെ രണ്ട് ഏകപക്ഷീയമായ പരിധികളും അനന്തമാണ്: , അതിനാൽ, ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ രണ്ടാമത്തെ തരത്തിലുള്ള ഒരു വിരാമം നേരിടുന്നു.

എന്റെ ലേഖനങ്ങൾ കഴിയുന്നത്ര വൈവിധ്യമാർന്ന ഉള്ളടക്കം ഉപയോഗിച്ച് പൂരിപ്പിക്കാൻ ഞാൻ ശ്രമിക്കുന്നു, അതിനാൽ ഇതുവരെ നേരിട്ടിട്ടില്ലാത്ത ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫ് നോക്കാം:

സ്റ്റാൻഡേർഡ് സ്കീം അനുസരിച്ച്:

1) ഡിനോമിനേറ്റർ പൂജ്യത്തിലേക്ക് പോകുന്നതിനാൽ ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ല.

തീർച്ചയായും, ഫംഗ്‌ഷൻ പോയിന്റിൽ ഒരു തടസ്സം നേരിടുന്നുണ്ടെന്ന് നമുക്ക് ഉടനടി നിഗമനം ചെയ്യാം , എന്നാൽ ഈ അവസ്ഥയ്ക്ക് പലപ്പോഴും ആവശ്യമായ വിരാമത്തിന്റെ സ്വഭാവം തരംതിരിക്കുന്നത് നല്ലതാണ്. ഇതിനായി:

റെക്കോർഡ് ചെയ്യുന്നതിലൂടെ ഞങ്ങൾ ഉദ്ദേശിക്കുന്നത് ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കട്ടെ അനന്തമായ ഒരു നെഗറ്റീവ് നമ്പർ , കൂടാതെ എൻട്രിക്ക് കീഴിൽ - അനന്തമായ പോസിറ്റീവ് നമ്പർ.

ഏകപക്ഷീയമായ പരിധികൾ അനന്തമാണ്, അതിനർത്ഥം ഈ ഘട്ടത്തിൽ 2-ആം തരത്തിന്റെ ഒരു വിരാമം ഫംഗ്ഷൻ അനുഭവിക്കുന്നു എന്നാണ്. y-അക്ഷം ആണ് ലംബമായ ലക്ഷണംചാർട്ടിനായി.

രണ്ട് ഏകപക്ഷീയമായ പരിമിതികളും നിലനിൽക്കുന്നത് അസാധാരണമല്ല, എന്നാൽ അവയിലൊന്ന് മാത്രം അനന്തമാണ്, ഉദാഹരണത്തിന്:

ഇത് ഫംഗ്ഷന്റെ ഗ്രാഫ് ആണ്.

തുടർച്ചയ്ക്കുള്ള പോയിന്റ് ഞങ്ങൾ പരിശോധിക്കുന്നു:

1) ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ല.

2) നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കാം:

പ്രഭാഷണത്തിന്റെ അവസാന രണ്ട് ഉദാഹരണങ്ങളിൽ അത്തരം ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കുന്ന രീതിയെക്കുറിച്ച് നമ്മൾ സംസാരിക്കും, എന്നിരുന്നാലും പല വായനക്കാരും ഇതിനകം തന്നെ എല്ലാം കാണുകയും ഊഹിക്കുകയും ചെയ്തിട്ടുണ്ട്.

ഇടത് വശത്തെ പരിധി പരിമിതവും പൂജ്യത്തിന് തുല്യവുമാണ് (ഞങ്ങൾ "ബിന്ദുവിലേക്ക് പോകില്ല"), എന്നാൽ വലത് വശത്തെ പരിധി അനന്തമാണ്, ഗ്രാഫിന്റെ ഓറഞ്ച് ശാഖ അതിൻ്റെ അടുത്തേക്ക് അടുക്കുന്നു. ലംബമായ ലക്ഷണം, സമവാക്യം (കറുത്ത ഡോട്ടഡ് ലൈൻ) നൽകിയിരിക്കുന്നു.

അതിനാൽ പ്രവർത്തനം തകരാറിലാകുന്നു രണ്ടാമത്തെ തരത്തിലുള്ള നിർത്തലാക്കൽബിന്ദുവില് .

1-ആം തരത്തിലുള്ള ഒരു നിർത്തലാക്കലിനെ സംബന്ധിച്ചിടത്തോളം, പ്രവർത്തനം നിർത്തലാക്കുന്ന പോയിന്റിൽ തന്നെ നിർവചിക്കാം. ഉദാഹരണത്തിന്, ഒരു പീസ്വൈസ് ഫംഗ്ഷനായി കോർഡിനേറ്റുകളുടെ ഉത്ഭവത്തിൽ ഒരു കറുത്ത ബോൾഡ് ഡോട്ട് ഇടാൻ മടിക്കേണ്ടതില്ല. വലതുവശത്ത് ഒരു ഹൈപ്പർബോളയുടെ ഒരു ശാഖയുണ്ട്, വലതുവശത്തെ പരിധി അനന്തമാണ്. ഈ ഗ്രാഫ് എങ്ങനെയുണ്ടെന്ന് മിക്കവാറും എല്ലാവർക്കും ധാരണയുണ്ടെന്ന് ഞാൻ കരുതുന്നു.

എല്ലാവരും ആകാംക്ഷയോടെ കാത്തിരുന്നത്:

തുടർച്ചയ്ക്കായി ഒരു ഫംഗ്ഷൻ എങ്ങനെ പരിശോധിക്കാം?

ഒരു ഘട്ടത്തിലെ തുടർച്ചയ്‌ക്കായുള്ള ഒരു ഫംഗ്‌ഷന്റെ പഠനം ഇതിനകം സ്ഥാപിതമായ ഒരു പതിവ് സ്കീം അനുസരിച്ചാണ് നടത്തുന്നത്, അതിൽ തുടർച്ചയുടെ മൂന്ന് വ്യവസ്ഥകൾ പരിശോധിക്കുന്നു:

ഉദാഹരണം 1

പ്രവർത്തനം പര്യവേക്ഷണം ചെയ്യുക

പരിഹാരം:

1) സ്കോപ്പിനുള്ളിലെ ഒരേയൊരു പോയിന്റ് ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ല.

2) നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കാം:

ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും തുല്യവുമാണ്.

അങ്ങനെ, ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ നീക്കം ചെയ്യാവുന്ന ഒരു തടസ്സം നേരിടുന്നു.

ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് എങ്ങനെയിരിക്കും?

ലളിതമാക്കാൻ ഞാൻ ആഗ്രഹിക്കുന്നു , ഒരു സാധാരണ പരവലയം ലഭിക്കുന്നത് പോലെ തോന്നുന്നു. പക്ഷേയഥാർത്ഥ പ്രവർത്തനം പോയിന്റിൽ നിർവചിച്ചിട്ടില്ല, അതിനാൽ ഇനിപ്പറയുന്ന ക്ലോസ് ആവശ്യമാണ്:

നമുക്ക് ഡ്രോയിംഗ് ഉണ്ടാക്കാം:

ഉത്തരം: നീക്കം ചെയ്യാവുന്ന വിരാമം നേരിടുന്ന പോയിന്റ് ഒഴികെ, മുഴുവൻ സംഖ്യാ രേഖയിലും പ്രവർത്തനം തുടർച്ചയായി തുടരുന്നു.

ഫംഗ്ഷൻ നല്ലതോ അല്ലാത്തതോ ആയ രീതിയിൽ കൂടുതൽ നിർവചിക്കാം, എന്നാൽ വ്യവസ്ഥ അനുസരിച്ച് ഇത് ആവശ്യമില്ല.

ഇതൊരു വിദൂര ഉദാഹരണമാണെന്ന് നിങ്ങൾ പറയുന്നുണ്ടോ? ഒരിക്കലുമില്ല. ഇത് പ്രായോഗികമായി ഡസൻ കണക്കിന് തവണ സംഭവിച്ചു. സൈറ്റിന്റെ മിക്കവാറും എല്ലാ ജോലികളും യഥാർത്ഥ സ്വതന്ത്ര ജോലിയിൽ നിന്നും ടെസ്റ്റുകളിൽ നിന്നും വരുന്നു.

നമുക്ക് പ്രിയപ്പെട്ട മൊഡ്യൂളുകൾ ഒഴിവാക്കാം:

ഉദാഹരണം 2

പ്രവർത്തനം പര്യവേക്ഷണം ചെയ്യുക തുടർച്ചയ്ക്കായി. ഫംഗ്ഷൻ നിർത്തലാക്കലുകൾ നിലവിലുണ്ടെങ്കിൽ അവയുടെ സ്വഭാവം നിർണ്ണയിക്കുക. ഡ്രോയിംഗ് എക്സിക്യൂട്ട് ചെയ്യുക.

പരിഹാരം: ചില കാരണങ്ങളാൽ, വിദ്യാർത്ഥികൾ ഭയപ്പെടുന്നു, ഒരു മൊഡ്യൂൾ ഉള്ള പ്രവർത്തനങ്ങൾ ഇഷ്ടപ്പെടുന്നില്ല, എന്നിരുന്നാലും അവയിൽ സങ്കീർണ്ണമായ ഒന്നും തന്നെയില്ല. അത്തരം കാര്യങ്ങളിൽ ഞങ്ങൾ ഇതിനകം പാഠത്തിൽ അല്പം സ്പർശിച്ചിട്ടുണ്ട്. ഗ്രാഫുകളുടെ ജ്യാമിതീയ രൂപാന്തരങ്ങൾ. മൊഡ്യൂൾ നെഗറ്റീവ് അല്ലാത്തതിനാൽ, ഇത് ഇനിപ്പറയുന്ന രീതിയിൽ വിപുലീകരിക്കുന്നു: , ഇവിടെ "ആൽഫ" എന്നത് ചില പദപ്രയോഗമാണ്. IN ഈ സാഹചര്യത്തിൽ, ഞങ്ങളുടെ ഫംഗ്‌ഷൻ കഷണങ്ങളായി എഴുതണം: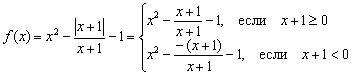

എന്നാൽ രണ്ട് കഷണങ്ങളുടെയും ഭിന്നസംഖ്യകൾ കുറയ്ക്കണം. മുൻ ഉദാഹരണത്തിലെന്നപോലെ കുറയ്ക്കൽ, അനന്തരഫലങ്ങളില്ലാതെ നടക്കില്ല. ഡിനോമിനേറ്റർ പൂജ്യത്തിലേക്ക് പോകുന്നതിനാൽ യഥാർത്ഥ പ്രവർത്തനം പോയിന്റിൽ നിർവചിച്ചിട്ടില്ല. അതിനാൽ, സിസ്റ്റം അധികമായി വ്യവസ്ഥ വ്യക്തമാക്കുകയും ആദ്യത്തെ അസമത്വം കർശനമാക്കുകയും വേണം:

ഇപ്പോൾ വളരെ കുറിച്ച് ഉപയോഗപ്രദമായ സ്വീകരണംപരിഹാരങ്ങൾ: ഒരു ഡ്രാഫ്റ്റിൽ ടാസ്‌ക്ക് അന്തിമമാക്കുന്നതിന് മുമ്പ്, ഒരു ഡ്രോയിംഗ് നിർമ്മിക്കുന്നത് പ്രയോജനകരമാണ് (അത് വ്യവസ്ഥകൾ അനുസരിച്ച് ആവശ്യമാണോ അല്ലയോ എന്നത് പരിഗണിക്കാതെ). ഒന്നാമതായി, തുടർച്ചയുടെ പോയിന്റുകളും നിർത്തലാക്കുന്നതിന്റെ പോയിന്റുകളും ഉടനടി കാണാൻ ഇത് സഹായിക്കും, രണ്ടാമതായി, ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്തുമ്പോൾ ഇത് 100% പിശകുകളിൽ നിന്ന് നിങ്ങളെ സംരക്ഷിക്കും.

നമുക്ക് ഡ്രോയിംഗ് ചെയ്യാം. ഞങ്ങളുടെ കണക്കുകൂട്ടലുകൾക്ക് അനുസൃതമായി, പോയിന്റിന്റെ ഇടതുവശത്ത് ഒരു പരാബോളയുടെ (നീല നിറം) ഒരു ഭാഗം വരയ്ക്കേണ്ടത് ആവശ്യമാണ്, വലതുവശത്ത് - ഒരു പരവലയത്തിന്റെ ഒരു ഭാഗം (ചുവപ്പ് നിറം), അതേസമയം ഫംഗ്ഷൻ നിർവചിച്ചിട്ടില്ല പോയിന്റ് തന്നെ:

സംശയമുണ്ടെങ്കിൽ, കുറച്ച് x മൂല്യങ്ങൾ എടുത്ത് ഫംഗ്ഷനിലേക്ക് പ്ലഗ് ചെയ്യുക (സാധ്യമായ മൈനസ് ചിഹ്നത്തെ മൊഡ്യൂൾ നശിപ്പിക്കുന്നുവെന്ന് ഓർമ്മിക്കുക) ഗ്രാഫ് പരിശോധിക്കുക.

നമുക്ക് തുടർച്ചയ്ക്കുള്ള പ്രവർത്തനം വിശകലനപരമായി പരിശോധിക്കാം:

1) ഫംഗ്ഷൻ പോയിന്റിൽ നിർവചിച്ചിട്ടില്ല, അതിനാൽ അത് അതിൽ തുടർച്ചയായി ഇല്ലെന്ന് നമുക്ക് ഉടൻ തന്നെ പറയാം.

2) നിർത്തലാക്കുന്നതിന്റെ സ്വഭാവം നമുക്ക് സ്ഥാപിക്കാം; ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കുന്നു:

ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും വ്യത്യസ്‌തവുമാണ്, അതായത് പോയിന്റിൽ ഒരു കുതിച്ചുചാട്ടത്തോടെ ഫംഗ്‌ഷൻ 1st തരത്തിലുള്ള ഒരു വിച്ഛേദിക്കപ്പെടുന്നു. പരിധികൾ കണ്ടെത്തുമ്പോൾ, ബ്രേക്ക് പോയിന്റിലെ പ്രവർത്തനം നിർവചിച്ചിട്ടുണ്ടോ ഇല്ലയോ എന്നത് പ്രശ്നമല്ലെന്ന് വീണ്ടും ശ്രദ്ധിക്കുക.

ഇപ്പോൾ അവശേഷിക്കുന്നത് ഡ്രാഫ്റ്റിൽ നിന്ന് ഡ്രോയിംഗ് കൈമാറുക (ഇത് ഗവേഷണത്തിന്റെ സഹായത്തോടെ നിർമ്മിച്ചതാണ് ;-)) കൂടാതെ ചുമതല പൂർത്തിയാക്കുക:

ഉത്തരം: ഒരു കുതിച്ചുചാട്ടത്തോടെ ആദ്യ തരത്തിലുള്ള ഒരു വിരാമം നേരിടുന്ന പോയിന്റ് ഒഴികെ, മുഴുവൻ സംഖ്യാരേഖയിലും പ്രവർത്തനം തുടർച്ചയായി തുടരുന്നു.

ചിലപ്പോൾ അവർക്ക് നിർത്തലാക്കൽ ജമ്പിന്റെ അധിക സൂചന ആവശ്യമാണ്. ഇത് ലളിതമായി കണക്കാക്കുന്നു - വലത് പരിധിയിൽ നിന്ന് നിങ്ങൾ ഇടത് പരിധി കുറയ്ക്കേണ്ടതുണ്ട്: , അതായത്, ബ്രേക്ക് പോയിന്റിൽ ഞങ്ങളുടെ പ്രവർത്തനം 2 യൂണിറ്റ് താഴേക്ക് ചാടി (മൈനസ് ചിഹ്നം നമ്മോട് പറയുന്നതുപോലെ).

ഉദാഹരണം 3

പ്രവർത്തനം പര്യവേക്ഷണം ചെയ്യുക തുടർച്ചയ്ക്കായി. ഫംഗ്ഷൻ നിർത്തലാക്കലുകൾ നിലവിലുണ്ടെങ്കിൽ അവയുടെ സ്വഭാവം നിർണ്ണയിക്കുക. ഒരു ഡ്രോയിംഗ് ഉണ്ടാക്കുക.

ഇത് നിങ്ങൾക്ക് സ്വന്തമായി പരിഹരിക്കാനുള്ള ഒരു ഉദാഹരണമാണ്, പാഠത്തിന്റെ അവസാനത്തിൽ ഒരു മാതൃകാ പരിഹാരം.

ഫംഗ്‌ഷൻ മൂന്ന് ഭാഗങ്ങൾ ഉൾക്കൊള്ളുമ്പോൾ, ടാസ്‌ക്കിന്റെ ഏറ്റവും ജനപ്രിയവും വ്യാപകവുമായ പതിപ്പിലേക്ക് പോകാം:

ഉദാഹരണം 4

തുടർച്ചയ്ക്കായി ഒരു ഫംഗ്ഷൻ പരിശോധിച്ച് ഫംഗ്ഷന്റെ ഒരു ഗ്രാഫ് പ്ലോട്ട് ചെയ്യുക .

പരിഹാരം: ഫംഗ്‌ഷന്റെ മൂന്ന് ഭാഗങ്ങളും അനുബന്ധ ഇടവേളകളിൽ തുടർച്ചയായി ഉണ്ടെന്ന് വ്യക്തമാണ്, അതിനാൽ കഷണങ്ങൾക്കിടയിൽ “ജംഗ്ഷൻ” ന്റെ രണ്ട് പോയിന്റുകൾ മാത്രം പരിശോധിക്കാൻ അവശേഷിക്കുന്നു. ആദ്യം, നമുക്ക് ഒരു ഡ്രാഫ്റ്റ് ഡ്രോയിംഗ് ഉണ്ടാക്കാം; ലേഖനത്തിന്റെ ആദ്യ ഭാഗത്ത് നിർമ്മാണ സാങ്കേതികതയെക്കുറിച്ച് മതിയായ വിശദമായി ഞാൻ അഭിപ്രായപ്പെട്ടു. ഒരേയൊരു കാര്യം, നമ്മുടെ ഏകവചന പോയിന്റുകൾ ശ്രദ്ധാപൂർവ്വം പിന്തുടരേണ്ടതുണ്ട്: അസമത്വം കാരണം, മൂല്യം നേർരേഖയുടേതാണ് (പച്ച ഡോട്ട്), അസമത്വം കാരണം, മൂല്യം പരാബോളയുടേതാണ് (ചുവന്ന ഡോട്ട്):


ശരി, തത്വത്തിൽ, എല്ലാം വ്യക്തമാണ് =) തീരുമാനം ഔപചാരികമാക്കാൻ മാത്രമാണ് അവശേഷിക്കുന്നത്. രണ്ട് “ചേരുന്ന” പോയിന്റുകൾക്കായി, ഞങ്ങൾ 3 തുടർച്ച വ്യവസ്ഥകൾ സാധാരണമായി പരിശോധിക്കുന്നു:

ഐ)തുടർച്ചയ്ക്കുള്ള പോയിന്റ് ഞങ്ങൾ പരിശോധിക്കുന്നു

1)

ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും വ്യത്യസ്‌തവുമാണ്, അതായത് പോയിന്റിൽ ഒരു കുതിച്ചുചാട്ടത്തോടെ ഫംഗ്‌ഷൻ 1st തരത്തിലുള്ള ഒരു വിച്ഛേദിക്കപ്പെടുന്നു.

വലത്, ഇടത് പരിധികൾ തമ്മിലുള്ള വ്യത്യാസമായി നമുക്ക് നിർത്തലാക്കൽ ജമ്പ് കണക്കാക്കാം:
, അതായത്, ഗ്രാഫ് ഒരു യൂണിറ്റ് ഉയർത്തി.

II)തുടർച്ചയ്ക്കുള്ള പോയിന്റ് ഞങ്ങൾ പരിശോധിക്കുന്നു

1) - ഫംഗ്ഷൻ ഒരു നിശ്ചിത പോയിന്റിൽ നിർവചിച്ചിരിക്കുന്നു.

2) ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്തുക:

- ഏകപക്ഷീയമായ പരിധികൾ പരിമിതവും തുല്യവുമാണ്, അതിനർത്ഥം ഒരു പൊതു പരിധി ഉണ്ടെന്നാണ്.

3) - ഒരു പോയിന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ പരിധി ഒരു നിശ്ചിത പോയിന്റിലെ ഈ ഫംഗ്‌ഷന്റെ മൂല്യത്തിന് തുല്യമാണ്.

അവസാന ഘട്ടത്തിൽ, ഞങ്ങൾ ഡ്രോയിംഗ് അന്തിമ പതിപ്പിലേക്ക് മാറ്റുന്നു, അതിനുശേഷം ഞങ്ങൾ അന്തിമ കോഡ് ഇടുന്നു:

ഉത്തരം: ഒരു കുതിച്ചുചാട്ടത്തോടെ ആദ്യ തരത്തിലുള്ള ഒരു വിച്ഛേദനം നേരിടുന്ന ഘട്ടം ഒഴികെ, മുഴുവൻ സംഖ്യാരേഖയിലും ഫംഗ്ഷൻ തുടർച്ചയായി തുടരുന്നു.

ഉദാഹരണം 5

തുടർച്ചയായി ഒരു ഫംഗ്ഷൻ പരിശോധിച്ച് അതിന്റെ ഗ്രാഫ് നിർമ്മിക്കുക .

നിങ്ങൾക്ക് സ്വയം പരിഹരിക്കാനുള്ള ഒരു ഉദാഹരണമാണിത്, ചെറിയ പരിഹാരംപാഠത്തിന്റെ അവസാനത്തിൽ ടാസ്ക്കിന്റെ ഏകദേശ മാതൃകയും.

ഒരു ഘട്ടത്തിൽ പ്രവർത്തനം തുടർച്ചയായിരിക്കണം, മറ്റൊന്നിൽ ഒരു വിരാമം ഉണ്ടായിരിക്കണം എന്ന ധാരണ നിങ്ങൾക്ക് ലഭിച്ചേക്കാം. പ്രായോഗികമായി, ഇത് എല്ലായ്പ്പോഴും അങ്ങനെയല്ല. ശേഷിക്കുന്ന ഉദാഹരണങ്ങൾ അവഗണിക്കാതിരിക്കാൻ ശ്രമിക്കുക - രസകരവും പ്രധാനപ്പെട്ടതുമായ നിരവധി സവിശേഷതകൾ ഉണ്ടാകും:

ഉദാഹരണം 6

ഒരു ഫംഗ്ഷൻ നൽകി . പോയിന്റുകളിൽ തുടർച്ചയ്ക്കായി പ്രവർത്തനം അന്വേഷിക്കുക. ഒരു ഗ്രാഫ് നിർമ്മിക്കുക.

പരിഹാരം: വീണ്ടും ഉടനടി ഡ്രാഫ്റ്റിലെ ഡ്രോയിംഗ് എക്സിക്യൂട്ട് ചെയ്യുക:

ഈ ഗ്രാഫിന്റെ പ്രത്യേകത, അബ്സിസ്സ അക്ഷത്തിന്റെ സമവാക്യം ഉപയോഗിച്ച് പീസ്വൈസ് ഫംഗ്ഷൻ നൽകുന്നു എന്നതാണ്. ഈ പ്രദേശം ഇവിടെ വരച്ചിരിക്കുന്നു പച്ച, കൂടാതെ ഒരു നോട്ട്ബുക്കിൽ ഇത് സാധാരണയായി ലളിതമായ പെൻസിൽ ഉപയോഗിച്ച് ബോൾഡായി ഹൈലൈറ്റ് ചെയ്യുന്നു. കൂടാതെ, തീർച്ചയായും, ഞങ്ങളുടെ ആട്ടുകൊറ്റന്മാരെ കുറിച്ച് മറക്കരുത്: മൂല്യം ടാൻജെന്റ് ബ്രാഞ്ചിന് (ചുവന്ന ഡോട്ട്) ആണ്, മൂല്യം നേർരേഖയുടേതാണ്.

ഡ്രോയിംഗിൽ നിന്ന് എല്ലാം വ്യക്തമാണ് - മുഴുവൻ നമ്പർ ലൈനിലും പ്രവർത്തനം തുടർച്ചയായി തുടരുന്നു, പരിഹാരം ഔപചാരികമാക്കുക എന്നതാണ് അവശേഷിക്കുന്നത്, ഇത് 3-4 സമാന ഉദാഹരണങ്ങൾക്ക് ശേഷം അക്ഷരാർത്ഥത്തിൽ പൂർണ്ണ ഓട്ടോമേഷനിലേക്ക് കൊണ്ടുവരുന്നു:

ഐ)തുടർച്ചയ്ക്കുള്ള പോയിന്റ് ഞങ്ങൾ പരിശോധിക്കുന്നു

1) - ഫംഗ്ഷൻ ഒരു നിശ്ചിത പോയിന്റിൽ നിർവചിച്ചിരിക്കുന്നു.

2) നമുക്ക് ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കാം:

, അതായത് ഒരു പൊതു പരിധി ഉണ്ട്.

അങ്ങനെയെങ്കിൽ, നിസ്സാരമായ ഒരു വസ്തുത ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കട്ടെ: ഒരു സ്ഥിരാങ്കത്തിന്റെ പരിധി സ്ഥിരമായതിന് തുല്യമാണ്. ഈ സാഹചര്യത്തിൽ, പൂജ്യത്തിന്റെ പരിധി പൂജ്യത്തിന് തുല്യമാണ് (ഇടത് കൈ പരിധി).

3) - ഒരു പോയിന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ പരിധി ഒരു നിശ്ചിത പോയിന്റിലെ ഈ ഫംഗ്‌ഷന്റെ മൂല്യത്തിന് തുല്യമാണ്.

അങ്ങനെ, ഒരു ബിന്ദുവിലെ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ചയുടെ നിർവചനം അനുസരിച്ച് ഒരു ബിന്ദുവിൽ ഒരു ഫംഗ്‌ഷൻ തുടർച്ചയായി തുടരുന്നു.

II)തുടർച്ചയ്ക്കുള്ള പോയിന്റ് ഞങ്ങൾ പരിശോധിക്കുന്നു

1) - ഫംഗ്ഷൻ ഒരു നിശ്ചിത പോയിന്റിൽ നിർവചിച്ചിരിക്കുന്നു.

2) ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്തുക:

ഇവിടെ - ഒന്നിന്റെ പരിധി യൂണിറ്റിന് തുല്യമാണ്.

- ഒരു പൊതു പരിധി ഉണ്ട്.

3) - ഒരു പോയിന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ പരിധി ഒരു നിശ്ചിത പോയിന്റിലെ ഈ ഫംഗ്‌ഷന്റെ മൂല്യത്തിന് തുല്യമാണ്.

അങ്ങനെ, ഒരു ബിന്ദുവിലെ ഒരു ഫംഗ്‌ഷന്റെ തുടർച്ചയുടെ നിർവചനം അനുസരിച്ച് ഒരു ബിന്ദുവിൽ ഒരു ഫംഗ്‌ഷൻ തുടർച്ചയായി തുടരുന്നു.

പതിവുപോലെ, ഗവേഷണത്തിന് ശേഷം ഞങ്ങൾ ഞങ്ങളുടെ ഡ്രോയിംഗ് അന്തിമ പതിപ്പിലേക്ക് മാറ്റുന്നു.

ഉത്തരം: പോയിന്റുകളിൽ പ്രവർത്തനം തുടർച്ചയായി നടക്കുന്നു.

ഈ അവസ്ഥയിൽ, തുടർച്ചയ്‌ക്കായി മുഴുവൻ പ്രവർത്തനവും പഠിക്കുന്നതിനെക്കുറിച്ച് ഞങ്ങളോട് ഒന്നും ചോദിച്ചിട്ടില്ല, മാത്രമല്ല ഇത് രൂപപ്പെടുത്തുന്നതിന് നല്ല ഗണിതശാസ്ത്ര രൂപമായി കണക്കാക്കുകയും ചെയ്യുന്നു. കൃത്യവും വ്യക്തവുംചോദിച്ച ചോദ്യത്തിനുള്ള ഉത്തരം. വഴിയിൽ, ഒരു ഗ്രാഫ് നിർമ്മിക്കാൻ വ്യവസ്ഥ ആവശ്യമില്ലെങ്കിൽ, നിങ്ങൾക്ക് ഉണ്ട് എല്ലാ അവകാശങ്ങളുംഇത് നിർമ്മിക്കരുത് (അധ്യാപകന് പിന്നീട് അത് ചെയ്യാൻ നിങ്ങളെ നിർബന്ധിക്കാമെങ്കിലും).

ഇത് സ്വയം പരിഹരിക്കുന്നതിനുള്ള ഒരു ചെറിയ ഗണിതശാസ്ത്ര "നാവ് ട്വിസ്റ്റർ":

ഉദാഹരണം 7

ഒരു ഫംഗ്ഷൻ നൽകി . പോയിന്റുകളിൽ തുടർച്ചയ്ക്കായി പ്രവർത്തനം അന്വേഷിക്കുക. എന്തെങ്കിലും ഉണ്ടെങ്കിൽ ബ്രേക്ക്‌പോയിന്റുകൾ തരംതിരിക്കുക. ഡ്രോയിംഗ് എക്സിക്യൂട്ട് ചെയ്യുക.

എല്ലാ "പദങ്ങളും" ശരിയായി "ഉച്ചരിക്കാൻ" ശ്രമിക്കുക =) കൂടാതെ ഗ്രാഫ് കൂടുതൽ കൃത്യമായി വരയ്ക്കുക, കൃത്യത, അത് എല്ലായിടത്തും അമിതമായിരിക്കില്ല;-)

നിങ്ങൾ ഓർക്കുന്നതുപോലെ, ഡ്രോയിംഗ് ഉടനടി ഒരു ഡ്രാഫ്റ്റായി പൂർത്തിയാക്കാൻ ഞാൻ ശുപാർശ ചെയ്തു, എന്നാൽ കാലാകാലങ്ങളിൽ ഗ്രാഫ് എങ്ങനെയുണ്ടെന്ന് നിങ്ങൾക്ക് പെട്ടെന്ന് കണ്ടെത്താൻ കഴിയാത്ത ഉദാഹരണങ്ങൾ നിങ്ങൾ കാണും. അതിനാൽ, ചില സന്ദർഭങ്ങളിൽ, ആദ്യം ഏകപക്ഷീയമായ പരിധികൾ കണ്ടെത്തുന്നത് പ്രയോജനകരമാണ്, അതിനുശേഷം മാത്രം, പഠനത്തെ അടിസ്ഥാനമാക്കി, ശാഖകൾ ചിത്രീകരിക്കുക. അവസാന രണ്ട് ഉദാഹരണങ്ങളിൽ ചില ഏകപക്ഷീയമായ പരിധികൾ കണക്കാക്കുന്നതിനുള്ള ഒരു സാങ്കേതികത കൂടി ഞങ്ങൾ പഠിക്കും:

ഉദാഹരണം 8

തുടർച്ചയ്ക്കായി ഫംഗ്ഷൻ പരിശോധിച്ച് അതിന്റെ സ്കീമാറ്റിക് ഗ്രാഫ് നിർമ്മിക്കുക.

പരിഹാരം: മോശം പോയിന്റുകൾ വ്യക്തമാണ്: (ഘാതകത്തിന്റെ ഡിനോമിനേറ്ററിനെ പൂജ്യമായി കുറയ്ക്കുന്നു) കൂടാതെ (മുഴുവൻ ഭിന്നസംഖ്യയുടെയും ഛേദത്തെ പൂജ്യമായി കുറയ്ക്കുന്നു). ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് എങ്ങനെയുണ്ടെന്ന് വ്യക്തമല്ല, അതിനർത്ഥം ആദ്യം കുറച്ച് ഗവേഷണം നടത്തുന്നതാണ് നല്ലത്.