5.2. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль. Түгээлтийн полигон
Эхлээд харахад салангид санамсаргүй хэмжигдэхүүнийг тодорхойлохын тулд түүний бүх боломжит утгыг жагсаахад хангалттай юм шиг санагдаж магадгүй юм. Бодит байдал дээр энэ нь тийм биш юм: санамсаргүй хэмжигдэхүүнүүд ижил жагсаалттай байж болно боломжит утгууд, тэдгээрийн магадлал нь өөр өөр байдаг. Тиймээс дискрет санамсаргүй хэмжигдэхүүнийг тодорхойлохын тулд түүний бүх боломжит утгыг жагсаах нь хангалтгүй бөгөөд тэдгээрийн магадлалыг зааж өгөх шаардлагатай.
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуульболомжит утгууд ба тэдгээрийн магадлалын хоорондох захидал харилцааг дуудах; Үүнийг хүснэгт, аналитик (томъёоны хэлбэрээр) болон графикаар зааж өгч болно.
Тодорхойлолт.Дурын үйл явдлын магадлалыг олох боломжийг олгодог аливаа дүрэм (хүснэгт, функц, график). А С (С– -орон зай дахь үйл явдлын алгебр ), тухайлбал санамсаргүй хэмжигдэхүүний хувь хүний утгуудын магадлал эсвэл эдгээр утгуудын багцыг гэж нэрлэдэг. санамсаргүй хэмжигдэхүүний тархалтын хууль(эсвэл зүгээр л: хуваарилалт). тухай s.v. Тэд "энэ нь хуваарилалтын өгөгдсөн хуульд захирагддаг" гэж хэлдэг.
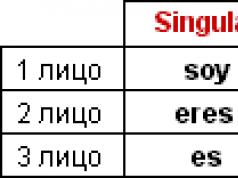
Болъё X– утгыг авдаг d.s.v X 1 , X 2 , …, x n,… (эдгээр утгуудын багц нь хязгаарлагдмал эсвэл тоолох боломжтой) тодорхой магадлалтай х би, Хаана би = 1,2,…, n,… Түгээлтийн хууль d.s.v. томъёог ашиглан тохируулахад тохиромжтой х би = П{X = x би) Хаана би = 1,2,…, n,..., энэ нь туршилтын үр дүнд r.v. Xүнэ цэнийг авах болно x би. d.s.v-ийн хувьд. Xхуваарилалтын хуулийг хэлбэрээр өгч болно түгээлтийн хүснэгтүүд:
|
x n | |||||
|
Р n |
Хүснэгт дэх салангид санамсаргүй хэмжигдэхүүний тархалтын хуулийг зааж өгөхдөө хүснэгтийн эхний мөрөнд боломжит утгууд, хоёр дахь мөрөнд тэдгээрийн магадлалууд орно. ийм хүснэгт гэж нэрлэдэг түгээлтийн ойролцоо.
Нэг туршилтанд санамсаргүй хэмжигдэхүүн нь зөвхөн нэг боломжит утгыг авдаг гэдгийг харгалзан үзээд бид үйл явдал гэж дүгнэж байна. X = x 1 , X = x 2 , ..., X = x nбүрэн бүлэг үүсгэх; иймээс эдгээр үйл явдлын магадлалын нийлбэр, i.e. Хүснэгтийн хоёр дахь эгнээний магадлалын нийлбэр нь нэгтэй тэнцүү, өөрөөр хэлбэл .
Хэрэв боломжит утгуудын багц бол Xхязгааргүй (тоологдох), дараа нь цуврал Р 1 + Р 2 + ... нийлж, нийлбэр нь нэгтэй тэнцүү байна.
Жишээ.Бэлэн мөнгөний хонжворт сугалаанд 100 ширхэг тасалбар олгосон байна. 50 рублийн нэг ялалт сугалаа. мөн 1 рублийн арван ялалт. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг ол X– нэг сугалааны тасалбар эзэмшигчийн хожих боломжтой үнэ.
Шийдэл.Боломжит утгуудыг бичье X: X 1 = 50, X 2 = 1, X 3 = 0. Эдгээр боломжит утгуудын магадлал нь: Р 1 = 0,01, Р 2 = 0,01, Р 3 = 1 – (Р 1 + Р 2)=0,89.
Шаардлагатай хуваарилалтын хуулийг бичье:
Хяналт: 0.01 + 0.1 + 0.89 =1.
Жишээ.Уг саванд 8 бөмбөлөг байгаагийн 5 нь цагаан, үлдсэн нь хар. Үүнээс санамсаргүй байдлаар 3 бөмбөг сугалж авна. Дээж дэх цагаан бөмбөлгийн тооны тархалтын хуулийг ол.
Шийдэл. r.v-ийн боломжит утгууд. X– дээжинд олон тооны цагаан бөмбөг байна X 1 = 0, X 2 = 1, X 3 = 2, X 4 = 3. Тэдний магадлал нь зохих ёсоор байх болно
 ;
;
 ;
; .
.
Хуваарилалтын хуулийг хүснэгт хэлбэрээр бичье.
|
|
|
|
|
Хяналт:  .
.
Хуваарилалтын хууль d.s.v. Хэрэв r.v-ийн боломжит утгуудыг абсцисса тэнхлэг дээр, эдгээр утгын магадлалыг ордны тэнхлэг дээр зурсан бол графикаар тодорхойлж болно. цэгүүдийг дараалан холбосон тасархай шугам ( X 1 , Р 1), (X 2 , Р 2),... дуудсан олон өнцөгт(эсвэл олон өнцөгт) хуваарилалт(5.1-р зургийг үз).

Цагаан будаа. 5.1. Түгээлтийн полигон
Одоо та илүү ихийг өгч болно нарийн тодорхойлолт d.s.v.
Тодорхойлолт.Санамсаргүй утга X нь салангид байна, хэрэв хязгаарлагдмал эсвэл тоолж болох тооны багц байгаа бол X 1 , X 2 , ... ийм байна П{X = x би } = х би > 0 (би= 1,2,…) ба х 1 + х 2 + Р 3 +… = 1.
Дискрет r.v дээрх математик үйлдлүүдийг тодорхойлъё.
Тодорхойлолт.Дүн (ялгаа, ажил) d.s.v. X, утгыг авч байна x бимагадлал бүхий х би = П{X = x би }, би = 1, 2, …, n, болон d.s.v. Ю, утгыг авч байна y j магадлал бүхий х j = П{Ю = y j }, j = 1, 2, …, м, d.s.v гэж нэрлэдэг. З = X + Ю (З = X – Ю, З = X Ю), утгыг авах z ij = x би + y j (z ij = x би – y j , z ij = x би y j) магадлал бүхий х ij = П{X = x би , Ю = y j) бүх заасан утгуудын хувьд биТэгээд j. Хэрэв зарим дүн давхцвал x би + y j (ялгаа x би – y j, ажилладаг x би y j) харгалзах магадлалыг нэмнэ.
Тодорхойлолт.Ажил d.s.v. дээр тоо s d.s.v гэж нэрлэдэг. cX, утгыг авч байна -тайx бимагадлал бүхий х би = П{X = x би }.
Тодорхойлолт.Хоёр d.s.v. XТэгээд Югэж нэрлэдэг бие даасан, хэрэв үйл явдал ( X = x би } = А биТэгээд ( Ю = y j } = Б jхэнд ч бие даасан би = 1, 2, …, n, j = 1, 2, …, м, тэр бол
Үгүй бол r.v. дуудсан хамааралтай. Хэд хэдэн r.v. Хэрэв тэдгээрийн аль нэгнийх нь тархалтын хууль нь бусад хэмжигдэхүүнүүд ямар боломжит утгыг авахаас хамаарахгүй бол харилцан бие даасан гэж нэрлэдэг.
Хамгийн түгээмэл хэрэглэгддэг хэд хэдэн түгээлтийн хуулиудыг авч үзье.
Магадлалын онолын үндсэн ойлголтуудад зориулсан хичээлийн хэсэгт бид санамсаргүй хэмжигдэхүүний тухай маш чухал ойлголтыг аль хэдийн танилцуулсан. Энд бид өгөх болно Цаашдын хөгжилЭнэ ойлголт бөгөөд санамсаргүй хэмжигдэхүүнийг дүрсэлж, шинжилж болох арга замыг заана.
Өмнө дурьдсанчлан, санамсаргүй хэмжигдэхүүн нь туршилтын үр дүнд нэг буюу өөр утгыг авч болох хэмжигдэхүүн юм, гэхдээ аль нь болохыг урьдчилан мэдэхгүй. Бид мөн тасралтгүй (дискрет) болон санамсаргүй хэмжигдэхүүнүүдийг ялгахаар тохиролцсон тасралтгүй төрөл. Тасралтгүй хэмжигдэхүүний боломжит утгыг урьдчилан жагсааж болно. Тасралтгүй хэмжигдэхүүний боломжит утгыг урьдчилан жагсаах боломжгүй бөгөөд тодорхой цоорхойг тасралтгүй дүүргэдэг.
Тасралтгүй санамсаргүй хэмжигдэхүүнүүдийн жишээ:
1) гурван зоос шидэх үед сүлдний харагдах тоо (боломжтой утга 0, 1, 2, 3);
2) ижил туршилтаар сүлд харагдах давтамж (боломжтой утгууд);
3) таван элементээс бүрдэх төхөөрөмж дэх бүтэлгүйтсэн элементүүдийн тоо (боломжтой утгууд нь 0, 1, 2, 3, 4, 5);
4) нисэх онгоцыг идэвхгүй болгоход хангалттай тооны цохилтын тоо (боломжтой утгууд 1, 2, 3, ..., n, ...);
5) агаарын тулалдаанд устгасан онгоцны тоо (боломжтой утгууд 0, 1, 2, ..., N, тулалдаанд оролцсон нийт нисэх онгоцны тоо хаана байна).
Тасралтгүй санамсаргүй хэмжигдэхүүнүүдийн жишээ:
1) галлах үед цохилтын цэгийн абсцисса (ординат);
2) цохилтын цэгээс зорилтот төв хүртэлх зай;
3) өндрийн тоолуурын алдаа;
4) радио хоолойн гэмтэлгүй ажиллах хугацаа.
Дараахь зүйлд санамсаргүй хэмжигдэхүүнийг том үсгээр, тэдгээрийн боломжит утгыг харгалзах жижиг үсгээр тэмдэглэхийг зөвшөөрье. Жишээлбэл, - гурван цохилтоор цохилтын тоо; боломжит утгууд: .
Боломжит утгууд бүхий тасархай санамсаргүй хэмжигдэхүүнийг авч үзье. Эдгээр утга тус бүр нь боломжтой боловч тодорхой биш бөгөөд X утга нь тус бүрийг тодорхой магадлалтайгаар авч болно. Туршилтын үр дүнд X утга нь эдгээр утгуудын аль нэгийг авна, өөрөөр хэлбэл. Тохиромжгүй үйл явдлын бүрэн бүлгийн нэг нь тохиолдох болно:
Эдгээр үйл явдлын магадлалыг p үсгээр харгалзах индексээр тэмдэглэе.
Тохиромжгүй үйл явдлууд (5.1.1) бүрэн бүлгийг бүрдүүлдэг тул
тэдгээр. санамсаргүй хэмжигдэхүүний бүх боломжит утгуудын магадлалын нийлбэр нь нэгтэй тэнцүү байна. Энэ нийт магадлал нь хувь хүний утгуудын дунд ямар нэгэн байдлаар хуваарилагдсан байдаг. Хэрэв бид энэ тархалтыг зааж өгвөл санамсаргүй хэмжигдэхүүнийг магадлалын үүднээс бүрэн тайлбарлах болно, i.e. (5.1.1) үйл явдал тус бүрд яг ямар магадлал байгааг харуулъя. Үүгээр бид санамсаргүй хэмжигдэхүүний тархалтын хууль гэгдэх болно.
Санамсаргүй хэмжигдэхүүний тархалтын хууль гэдэг нь санамсаргүй хэмжигдэхүүний боломжит утгууд болон харгалзах магадлалуудын хоорондын холбоог тогтоодог аливаа харилцаа юм. Бид санамсаргүй хэмжигдэхүүнийг өгөгдсөн тархалтын хуульд захирагддаг гэж хэлэх болно.
Тасралтгүй санамсаргүй хэмжигдэхүүний тархалтын хуулийг тодорхойлж болох хэлбэрийг тогтооцгооё. Хамгийн энгийн хэлбэрЭнэ хуулийн тодорхойлолт нь санамсаргүй хэмжигдэхүүний боломжит утгууд болон холбогдох магадлалыг жагсаасан хүснэгт юм.

Ийм хүснэгтийг бид санамсаргүй хэмжигдэхүүний тархалтын цуваа гэж нэрлэх болно.
Түгээлтийн цувралыг илүү нүдээр харуулахын тулд тэд ихэвчлэн түүний график дүрслэлд ханддаг: санамсаргүй хэмжигдэхүүний боломжит утгуудыг абсцисса тэнхлэгийн дагуу, эдгээр утгын магадлалыг ордны тэнхлэгийн дагуу зурдаг. Тодорхой болгохын тулд үүссэн цэгүүдийг шулуун сегментээр холбодог. Ийм дүрсийг тархалтын олон өнцөгт гэж нэрлэдэг (Зураг 5.1.1). Тархалтын олон өнцөгт нь тархалтын цувралын нэгэн адил санамсаргүй хэмжигдэхүүнийг бүрэн тодорхойлдог; энэ нь хуваарилалтын хуулийн нэг хэлбэр юм.

Заримдаа түгээлтийн цувралын "механик" тайлбар нь тохиромжтой байдаг. Нэгтэй тэнцүү тодорхой масс нь абсцисса тэнхлэгийн дагуу хуваарилагдсан бөгөөд массууд тус тусад нь тус тусад нь цэгүүдэд төвлөрдөг гэж төсөөлөөд үз дээ. Дараа нь тархалтын цувааг абсцисса тэнхлэгт байрлах зарим масстай материаллаг цэгүүдийн систем гэж тайлбарладаг.
Тасралтгүй санамсаргүй хэмжигдэхүүний хэд хэдэн жишээг тархалтын хуультай нь авч үзье.
Жишээ 1. Үйл явдал гарч болох эсвэл харагдахгүй байж болох нэг туршилтыг хийдэг. Үйл явдлын магадлал 0.3 байна. Санамсаргүй хэмжигдэхүүнийг авч үздэг - тухайн туршилт дахь үйл явдлын тохиолдлын тоо (жишээ нь, тохиолдлын санамсаргүй хэмжигдэхүүн, хэрэв гарч ирвэл 1, харагдахгүй бол 0 утгыг авна). Тархалтын цуваа ба магнитудын тархалтын полигоныг байгуул.
Шийдэл. Утга нь зөвхөн хоёр утгатай: 0 ба 1.

Тархалтын олон өнцөгтийг Зураг дээр үзүүлэв. 5.1.2.

Жишээ 2. Буудагч бай руу гурван удаа буудаж байна. Буудсан болгонд бай онох магадлал 0.4 байна. Оносон тус бүрийн хувьд мэргэн бууч 5 оноо авдаг. Авсан онооны тоогоор хуваарилах цувралыг байгуул.
Шийдэл. Авсан онооны тоог тэмдэглэе. Боломжит утгууд: .
Туршилтыг давтах теоремыг ашиглан бид эдгээр утгын магадлалыг олдог.

Утга хуваарилалтын цуврал нь дараах хэлбэртэй байна.

Тархалтын олон өнцөгтийг Зураг дээр үзүүлэв. 5.1.3.

Жишээ 3. Нэг туршилтанд тохиолдох үйл явдлын магадлал нь тэнцүү байна. Хэд хэдэн бие даасан туршилтуудыг хийдэг бөгөөд энэ нь үйл явдлын анхны тохиолдол гарах хүртэл үргэлжилж, дараа нь туршилтыг зогсооно. Санамсаргүй хувьсагч - хийсэн туршилтын тоо. Үнийн хуваарилалтын цувралыг байгуул.
Шийдэл. Боломжит утгууд: 1, 2, 3, ... (онолын хувьд тэд юугаар ч хязгаарлагдахгүй). Хэмжигдэхүүн 1-ийн утгыг авахын тулд эхний туршилтанд үйл явдал тохиолдох шаардлагатай; магадлал тэнцүү байна. Хэмжигдэхүүн 2-ын утгыг авахын тулд тухайн үйл явдал эхний туршилтанд харагдахгүй, харин хоёр дахь удаагаа гарч ирэх шаардлагатай; магадлал нь тэнцүү, хаана гэх мэт. Утга хуваарилалтын цуврал нь дараах хэлбэртэй байна.

Тохиолдлын тархалтын полигоны эхний таван ординатыг Зураг дээр үзүүлэв. 5.1.4.

Жишээ 4. Буудагч 4 сумтай бай руу эхний цохилт хүртэл буудаж байна. Буудсан тус бүрийн цохилтын магадлал 0.6 байна. Зарлагдаагүй үлдсэн сумны хэмжээг хуваарилах цувралыг байгуул.
Шийдэл. Санамсаргүй хэмжигдэхүүн - ашиглагдаагүй хайрцагны тоо - дөрвөн боломжит утгатай: 0, 1, 2 ба 3. Эдгээр утгын магадлал нь тэнцүү байна:

Утга хуваарилалтын цуврал нь дараах хэлбэртэй байна.

Тархалтын олон өнцөгтийг Зураг дээр үзүүлэв. 5.1.5.

Жишээ 5. Техникийн төхөөрөмжийг янз бүрийн нөхцөлд ашиглах боломжтой бөгөөд үүнээс хамааран үе үе тохируулга хийх шаардлагатай болдог. Төхөөрөмжийг нэг удаа ашиглах үед энэ нь санамсаргүй байдлаар таатай эсвэл тааламжгүй горимд орж болно. Тааламжтай горимд төхөөрөмж нь тохируулгагүйгээр гурван хэрэглээг тэсвэрлэх чадвартай; дөрөв дэхээс өмнө үүнийг тохируулах хэрэгтэй. Тааламжгүй горимд төхөөрөмжийг эхний хэрэглээний дараа тохируулах шаардлагатай. Төхөөрөмж таатай горимд орох магадлал 0.7, таагүй горимд орох магадлал 0.3 байна. Санамсаргүй хэмжигдэхүүнийг авч үздэг - тохируулахаас өмнө төхөөрөмжийн ашиглалтын тоо. Түүний түгээлтийн цувралыг байгуул.
Шийдэл. Санамсаргүй хэмжигдэхүүн нь 1, 2 ба 3 гэсэн гурван боломжит утгатай байна. , магадлал нь төхөөрөмжийг анх удаа ашиглах үед тааламжгүй горимд орох магадлалтай тэнцүү, өөрөөр хэлбэл. . Утга 2-ын утгыг авахын тулд төхөөрөмж эхний хэрэглээний үед таатай горимд байх ёстой бөгөөд хоёр дахь ашиглалтын үед тааламжгүй горимд байх ёстой; энэ магадлал ![]() . Утга 3-ын утгыг авахын тулд төхөөрөмж эхний хоёр удаа таатай горимд байх ёстой (гурав дахь удаагаа ч гэсэн тохируулах шаардлагатай болно). Үүний магадлал тэнцүү байна
. Утга 3-ын утгыг авахын тулд төхөөрөмж эхний хоёр удаа таатай горимд байх ёстой (гурав дахь удаагаа ч гэсэн тохируулах шаардлагатай болно). Үүний магадлал тэнцүү байна ![]() .
.
Утга хуваарилалтын цуврал нь дараах хэлбэртэй байна.

Тархалтын олон өнцөгтийг Зураг дээр үзүүлэв. 5.1.6.

Түгээлтийн функц
Өмнөх n°-д бид тархалтын цувааг тасархай санамсаргүй хэмжигдэхүүний бүрэн шинж чанар (тархалтын хууль) болгон танилцуулсан. Гэсэн хэдий ч энэ шинж чанар нь бүх нийтийнх биш юм; энэ нь зөвхөн тасархай санамсаргүй хэмжигдэхүүнүүдэд л байдаг. Үргэлжилсэн санамсаргүй хэмжигдэхүүнд ийм шинж чанарыг бий болгох боломжгүй гэдгийг харахад хялбар байдаг. Үнэн хэрэгтээ тасралтгүй санамсаргүй хэмжигдэхүүн нь тодорхой интервалыг ("тоолж болох олонлог" гэж нэрлэдэг) бүрэн дүүргэх хязгааргүй тооны боломжит утгатай байдаг. Ийм санамсаргүй хэмжигдэхүүний бүх боломжит утгыг жагсаасан хүснэгт үүсгэх боломжгүй юм. Түүнээс гадна, бид дараа нь харах болно, үргэлжилсэн санамсаргүй хэмжигдэхүүний бие даасан утга бүрт ихэвчлэн тэгээс өөр магадлал байдаггүй. Иймээс тасралтгүй санамсаргүй хэмжигдэхүүний хувьд тасархай хувьсагчийн хувьд байгаа утгаараа тархалтын цуваа байдаггүй. Гэсэн хэдий ч санамсаргүй хэмжигдэхүүний боломжит утгуудын өөр өөр талбарууд ижил магадлал багатай хэвээр байгаа бөгөөд тасралтгүй хувьсагчийн хувьд "магадлалын тархалт" байдаг боловч тасархай хэмжигдэхүүнтэй ижил утгаараа биш юм.
Энэхүү магадлалын тархалтыг тоон хувьд тодорхойлохын тулд тухайн үйл явдлын магадлалыг ашиглах нь тохиромжтой бөгөөд энэ нь одоогийн хувьсагч юм. Энэ үйл явдлын магадлал нь мэдээжийн хэрэг -ээс хамаарна, зарим функц байдаг. Энэ функцийг санамсаргүй хэмжигдэхүүний тархалтын функц гэж нэрлэх ба дараах байдлаар тэмдэглэнэ.
![]() . (5.2.1)
. (5.2.1)
Түгээлтийн функцийг заримдаа хуримтлагдсан тархалтын функц эсвэл хуримтлагдсан тархалтын хууль гэж нэрлэдэг.
Тархалтын функц нь санамсаргүй хэмжигдэхүүний хамгийн түгээмэл шинж чанар юм. Энэ нь бүх санамсаргүй хэмжигдэхүүнүүдэд байдаг: тасархай болон тасралтгүй. Тархалтын функц нь магадлалын үүднээс санамсаргүй хэмжигдэхүүнийг бүрэн тодорхойлдог, i.e. хуваарилалтын хуулийн нэг хэлбэр юм.
Түгээлтийн функцийн зарим ерөнхий шинж чанарыг томъёолъё.
1. Түгээлтийн функц нь түүний аргументийн буурдаггүй функц, i.e. цагт.
2. Хасах хязгааргүй үед тархалтын функц тэгтэй тэнцүү байна: .
3. Хязгааргүй нэмэх үед тархалтын функц нэгтэй тэнцүү байна: .
Эдгээр шинж чанаруудын хатуу нотолгоог өгөхгүйгээр бид тэдгээрийг геометрийн харааны тайлбарыг ашиглан дүрслэн харуулах болно. Үүнийг хийхийн тулд бид санамсаргүй хэмжигдэхүүнийг Ox тэнхлэг дээрх санамсаргүй цэг гэж үзэх болно (Зураг 5.2.1), туршилтын үр дүнд нэг эсвэл өөр байрлалыг авч болно. Дараа нь тархалтын функц нь туршилтын үр дүнд санамсаргүй цэг нь цэгийн зүүн талд унах магадлал юм.

Бид нэмэгдүүлэх болно , өөрөөр хэлбэл абсцисса тэнхлэгийн дагуу цэгийг баруун тийш шилжүүлнэ. Мэдээжийн хэрэг, энэ тохиолдолд санамсаргүй цэг зүүн тийш унах магадлал буурах боломжгүй; тиймээс тархалтын функц өсөх тусам буурч болохгүй.
Үүнийг баталгаажуулахын тулд бид цэгийг абсцисса дагуу зүүн тийш тодорхойгүй хугацаагаар шилжүүлэх болно. Энэ тохиолдолд хязгаарын зүүн талд санамсаргүй цэгийг цохих нь боломжгүй үйл явдал болно; Энэ үйл явдлын магадлал нь тэг байх хандлагатай гэдэгт итгэх нь зүйн хэрэг, i.e. .
Үүний нэгэн адил, цэгийг баруун тийш тодорхойгүй хугацаагаар шилжүүлснээр бид үйл явдал хязгаарлагдмал найдвартай болж байгаа эсэхийг баталгаажуулдаг.
Тархалтын функцийн график дотор ерөнхий тохиолдолнь буурахгүй функцийн график (Зураг 5.2.2), утга нь 0-ээс эхэлж 1-д хүрдэг бөгөөд тодорхой цэгүүдэд функц үсрэлт (тасралт) байж болно.

Тасралтгүй санамсаргүй хэмжигдэхүүний тархалтын цувааг мэдсэнээр энэ хувьсагчийн тархалтын функцийг хялбархан байгуулж болно. Үнэхээр,
![]() ,
,
нийлбэрийн тэмдгийн доорх тэгш бус байдал нь нийлбэр нь -ээс бага байгаа бүх утгуудад хамааралтай болохыг харуулж байна.
Одоогийн хувьсагч нь тасалдсан утгын боломжит утгуудын аль нэгээр дамжин өнгөрөхөд тархалтын функц огцом өөрчлөгдөж, үсрэлтийн хэмжээ нь энэ утгын магадлалтай тэнцүү байна.
Жишээ 1. Үйл явдал гарч болох эсвэл харагдахгүй байж болох нэг туршилтыг хийдэг. Үйл явдлын магадлал 0.3 байна. Санамсаргүй хэмжигдэхүүн - туршилтанд тохиолдсон үйл явдлын тоо (үйл явдлын санамсаргүй хэмжигдэхүүний шинж чанар). Түүний түгээлтийн функцийг байгуул.
Туршлага гэдэг нь судалж буй санамсаргүй үзэгдлийг ажиглах тодорхой нөхцөл байдал, үйлдлүүдийн хэрэгжилт юм. Туршилтыг чанарын болон тоон байдлаар тодорхойлж болно. Санамсаргүй хэмжигдэхүүн гэдэг нь туршилтын үр дүнд нэг буюу өөр утгыг авч болох хэмжигдэхүүн бөгөөд аль нь болохыг урьдчилж мэдэгддэггүй.
Санамсаргүй хэмжигдэхүүнийг ихэвчлэн (X,Y,Z) тэмдэглэдэг ба харгалзах утгуудыг (x,y,z)
Дискрет гэдэг нь бие биенээсээ тусгаарлагдсан бие даасан утгыг авдаг санамсаргүй хэмжигдэхүүнүүд бөгөөд хэт үнэлж болно. Тасралтгүй хэмжигдэхүүнүүдболомжит утгууд нь тодорхой хүрээг тасралтгүй дүүргэдэг. Санамсаргүй хэмжигдэхүүний тархалтын хууль нь санамсаргүй хэмжигдэхүүний боломжит утгууд ба харгалзах магадлалуудын хоорондын холбоог тогтоодог аливаа харилцаа юм. Түгээлтийн эгнээ ба олон өнцөгт. Хуваарилалтын хуулийн хамгийн энгийн хэлбэр дискрет утгатүгээлтийн цуврал юм. Түгээлтийн цувралын график тайлбар нь тархалтын полигон юм.
Та мөн өөрийн сонирхож буй мэдээллээ шинжлэх ухааны хайлтын систем Otvety.Online-аас олж болно. Хайлтын маягтыг ашиглана уу:
Сэдвийн талаар дэлгэрэнгүй 13. Дискрет санамсаргүй хэмжигдэхүүн. Түгээлтийн полигон. Санамсаргүй хэмжигдэхүүнтэй үйлдлүүд, жишээ нь:
- 13. Дискрет санамсаргүй хэмжигдэхүүн ба түүний тархалтын хууль. Түгээлтийн полигон. Санамсаргүй хэмжигдэхүүнтэй үйлдлүүд. Жишээ.
- "Санамсаргүй хувьсагч" гэсэн ойлголт ба түүний тайлбар. Дискрет санамсаргүй хэмжигдэхүүн ба түүний тархалтын хууль (цуврал). Бие даасан санамсаргүй хэмжигдэхүүнүүд. Жишээ.
- 14. Санамсаргүй хэмжигдэхүүн, тэдгээрийн төрлүүд. Дискрет санамсаргүй хэмжигдэхүүний (DRV) магадлалын тархалтын хууль. Санамсаргүй хэмжигдэхүүн (SV) байгуулах аргууд.
- 16. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль. Дискрет санамсаргүй хэмжигдэхүүний тоон шинж чанар: математикийн хүлээлт, тархалт ба стандарт хазайлт.
- Дискрет санамсаргүй хэмжигдэхүүн дээрх математик үйлдлүүд болон Х, Ү бие даасан санамсаргүй хэмжигдэхүүнүүдийн өгөгдсөн тархалт дээр үндэслэн KX, X"1, X + K, XV-ийн тархалтын хуулийг бүтээх жишээнүүд.
- Санамсаргүй хэмжигдэхүүний тухай ойлголт. Дискрет хэргийг хуваарилах хууль. тоо хэмжээ. Санамсаргүй дээрх математик үйлдлүүд. тоо хэмжээ.
Санамсаргүй хэмжигдэхүүн: салангид ба тасралтгүй.
Стохастик туршилт хийх үед энгийн үйл явдлын орон зай үүсдэг - боломжит үр дүнэнэ туршилт. Энэ орон зайд анхан шатны үйл явдлууд өгөгдсөн гэж үздэг санамсаргүй утга X, хэрэв анхан шатны үйл явдал бүр тоотой холбоотой хууль (дүрэм) өгөгдсөн бол. Иймд санамсаргүй хэмжигдэхүүн X нь анхан шатны үйл явдлын орон зайд тодорхойлогдсон функц гэж үзэж болно.
■ Санамсаргүй хувьсагч- туршилт бүрт нэг юмуу өөрийг авдаг хэмжигдэхүүн тоон утга(аль нь урьдчилж мэдэгдэхгүй), урьдчилан тооцох боломжгүй санамсаргүй шалтгаанаас хамаарна. Санамсаргүй хэмжигдэхүүнийг том үсгээр тэмдэглэнэ Латин цагаан толгой, мөн санамсаргүй хэмжигдэхүүний боломжит утгууд бага байна. Тиймээс үхэл шидэх үед x тоотой холбоотой үйл явдал тохиолддог бөгөөд x нь өнхрүүлсэн онооны тоо юм. Онооны тоо нь санамсаргүй хэмжигдэхүүн бөгөөд 1, 2, 3, 4, 5, 6 тоонууд нь энэ утгын боломжит утгууд юм. Буунаас харвах үед пуужингийн явах зай нь мөн санамсаргүй хэмжигдэхүүн (харааны суурилуулалт, салхины хүч, чиглэл, температур болон бусад хүчин зүйлээс хамаарч) бөгөөд энэ утгын боломжит утгууд хамаарна. тодорхой интервалд (a; b).
■ Дискрет санамсаргүй хэмжигдэхүүн- тодорхой магадлал бүхий тусдаа, тусгаарлагдсан боломжит утгуудыг авдаг санамсаргүй хэмжигдэхүүн. Дискрет санамсаргүй хэмжигдэхүүний боломжит утгуудын тоо нь төгсгөлтэй эсвэл хязгааргүй байж болно.
■ Тасралтгүй санамсаргүй хэмжигдэхүүн- хязгаарлагдмал эсвэл хязгааргүй интервалаас бүх утгыг авах боломжтой санамсаргүй хэмжигдэхүүн. Тасралтгүй санамсаргүй хэмжигдэхүүний боломжит утгуудын тоо хязгааргүй байна.
Жишээлбэл, шоо шидэх үед авсан онооны тоо, тестийн оноо нь салангид санамсаргүй хэмжигдэхүүн; Буунаас буудах үед сумны нисэх зай, сургалтын материалыг эзэмших цаг хугацааны хэмжилтийн алдаа, хүний өндөр, жин зэрэг нь тасралтгүй санамсаргүй хэмжигдэхүүн юм.
Санамсаргүй хэмжигдэхүүний тархалтын хууль- санамсаргүй хэмжигдэхүүний боломжит утгууд ба тэдгээрийн магадлалын хоорондын хамаарал, жишээлбэл. Боломжит x i утга бүр нь санамсаргүй хэмжигдэхүүн энэ утгыг авч болох p i магадлалтай холбоотой. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг хүснэгтээр (хүснэгт хэлбэрээр), аналитик (томьёоны хэлбэрээр) болон графикаар тодорхойлж болно.
Дискрет санамсаргүй хэмжигдэхүүн X нь p 1, p 2, …, p n магадлал бүхий x 1, x 2, …, x n утгуудыг тус тус авъя, өөрөөр хэлбэл. P(X=x 1) = p 1, P(X=x 2) = p 2, …, P(X=x n) = p n. Энэ хэмжигдэхүүний тархалтын хуулийг хүснэгтэд зааж өгөхдөө хүснэгтийн эхний мөрөнд x 1 , x 2 , ..., x n боломжит утгууд, хоёр дахь мөрөнд тэдгээрийн магадлалыг агуулна.
| X | x 1 | x 2 | … | x n |
| х | х 1 | p2 | … | p n |
Туршилтын үр дүнд Х дискрет санамсаргүй хэмжигдэхүүн нь боломжит утгуудын зөвхөн нэгийг нь авдаг тул X=x 1, X=x 2, ..., X=x n үйл явдлууд нь хосоороо үл нийцэх бүрэн бүлгийг бүрдүүлдэг. үйл явдлууд, тиймээс эдгээр үйл явдлын магадлалын нийлбэр нь нэгтэй тэнцүү байна, i.e. p 1 + p 2 +… + p n =1.
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль. Тархалтын олон өнцөгт (олон өнцөгт).
Таны мэдэж байгаагаар санамсаргүй хэмжигдэхүүн нь тухайн тохиолдлоос хамааран тодорхой утгыг авч чаддаг хувьсагч юм. Санамсаргүй хэмжигдэхүүнийг тэмдэглэнэ том үсгээрЛатин цагаан толгой (X, Y, Z) ба тэдгээрийн утгыг харгалзах жижиг үсгээр (x, y, z) бичнэ. Санамсаргүй хэмжигдэхүүнийг тасархай (дискрет) ба тасралтгүй гэж хуваадаг.
Дискрет санамсаргүй хэмжигдэхүүн нь тодорхой тэгээс өөр магадлал бүхий зөвхөн төгсгөлтэй эсвэл хязгааргүй (тоолж болох) утгыг авдаг санамсаргүй хэмжигдэхүүн юм.
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуульсанамсаргүй хэмжигдэхүүний утгыг тэдгээрийн магадлалтай холбодог функц юм. Хуваарилалтын хуулийг дараах аргуудын аль нэгээр тодорхойлж болно.
1. Хуваарилалтын хуулийг дараах хүснэгтээр өгч болно.
Энд λ>0, k = 0, 1, 2, … .
в) X санамсаргүй хэмжигдэхүүн нь x-ээс бага утгыг авах магадлалыг х утга тус бүрээр тодорхойлдог F(x) түгээлтийн функцийг ашиглан, өөрөөр хэлбэл. F(x) = P(X< x).
 |
F(x) функцийн шинж чанарууд
3. Түгээлтийн хуулийг графикаар - тархалтын олон өнцөгт (олон өнцөгт) -ээр тодорхойлж болно (даалгавар 3-ыг үз).
Зарим асуудлыг шийдэхийн тулд хуваарилалтын хуулийг мэдэх шаардлагагүй гэдгийг анхаарна уу. Зарим тохиолдолд хамгийн их туссан нэг буюу хэд хэдэн тоог мэдэхэд хангалттай чухал шинж чанаруудхуваарилалтын хууль. Энэ нь санамсаргүй хэмжигдэхүүний "дундаж" гэсэн утгыг агуулсан тоо, эсвэл заасан тоо байж болно. дундаж хэмжээсанамсаргүй хэмжигдэхүүний дундаж утгаас хазайлт. Ийм төрлийн тоонуудыг санамсаргүй хэмжигдэхүүний тоон шинж чанар гэж нэрлэдэг.
Дискрет санамсаргүй хэмжигдэхүүний үндсэн тоон шинж чанарууд:
- Дискрет санамсаргүй хэмжигдэхүүний математикийн хүлээлт (дундаж утга) M(X)=Σ x i p i .
Дуран тархалтын хувьд M(X)=np, Пуассон тархалтын хувьд M(X)=λ - Дискрет санамсаргүй хэмжигдэхүүний дисперс D(X)= M 2 эсвэл D(X) = M(X 2)− 2. X–M(X) ялгааг санамсаргүй хэмжигдэхүүнээс хазайлт гэнэ математикийн хүлээлт.
Дуран тархалтын хувьд D(X)=npq, Пуассон тархалтын хувьд D(X)=λ - Стандарт хэлбэлзэл ( стандарт хэлбэлзэл) σ(X)=√D(X).
· Вариацын цувралын танилцуулгыг тодорхой болгох үүднээс их ач холбогдолграфик дүрстэй. Графикийн хувьд вариацын цувралыг олон өнцөгт, гистограм, хуримтлал хэлбэрээр дүрсэлж болно.
· Тархалтын олон өнцөгтийг (шууд утгаараа тархалтын олон өнцөгт) тэгш өнцөгт координатын системд баригдсан тасархай шугам гэж нэрлэдэг. Шинж чанарын утгыг абсцисса, харгалзах давтамж (эсвэл харьцангуй давтамж) - ординат дээр зурна. Цэгүүд (эсвэл) шулуун шугамын сегментүүдээр холбогдож, түгээлтийн полигоныг олж авна. Ихэнх тохиолдолд олон өнцөгтийг салангид дүрслэлд ашигладаг вариацын цуврал, гэхдээ тэдгээрийг бас ашиглаж болно интервалын цуврал. Энэ тохиолдолд эдгээр интервалуудын дунд цэгүүдэд тохирох цэгүүдийг абсцисса тэнхлэг дээр зурна.