Budeme uvažovat o výrazech Fourierovy řady v trigonometrické a komplexní formě a také věnovat pozornost Dirichletovým podmínkám pro konvergenci Fourierovy řady. Kromě toho se podrobně zastavíme u vysvětlení takového pojmu, jako je záporná frekvence spektra signálu, která často způsobuje potíže při seznámení se s teorií spektrální analýzy.
Periodický signál. Trigonometrické Fourierovy řady
Nechť existuje periodický signál spojitého času, který se opakuje s periodou c, tzn. , kde je libovolné celé číslo.
Obrázek 1 ukazuje jako příklad sekvenci pravoúhlých pulzů o délce c, opakujících se s periodou c.
Obrázek 1. Periodická sekvence
obdélníkové impulsy
Z průběhu matematické analýzy je známo, že systém goniometrických funkcí
S vícenásobnými frekvencemi, kde rad/s je celé číslo, tvoří ortonormální základ pro rozklad periodických signálů s periodou splňující Dirichletovy podmínky. Dirichletovy podmínky pro konvergenci Fourierovy řady vyžadují, aby byl na segmentu specifikován periodický signál a aby byly splněny následující podmínky:
Například periodická funkce 
nesplňuje Dirichletovy podmínky, protože funkce má nespojitosti druhého druhu a nabývá nekonečných hodnot v , kde je libovolné celé číslo. Takže funkce nelze zastupovat vedle Fouriera. Můžete také uvést příklad funkce 
, který je omezený, ale také nesplňuje Dirichletovy podmínky, protože má nekonečný počet extrémních bodů, jak se blíží nule. Graf funkce zobrazeno na obrázku 2.
Obrázek 2. Graf funkcí :
a - dvě periody opakování; b - v okolí
Obrázek 2a ukazuje dvě periody opakování funkce , a na obrázku 2b - oblast v blízkosti . Je vidět, že jak se blíží nule, kmitání frekvence nekonečně roste a takovou funkci nelze reprezentovat Fourierovou řadou, protože není po částech monotónní.
Je třeba poznamenat, že v praxi neexistují žádné signály s nekonečnými hodnotami proudu nebo napětí. Funkce s nekonečným počtem extrémů typu se také nevyskytují v aplikovaných problémech. Všechny reálné periodické signály splňují Dirichletovy podmínky a mohou být reprezentovány nekonečnou trigonometrickou Fourierovou řadou ve tvaru:
Ve výrazu (2) koeficient udává konstantní složku periodického signálu.
Ve všech bodech, kde je signál spojitý, Fourierova řada (2) konverguje k hodnotám daného signálu a v bodech nespojitosti prvního druhu - k průměrné hodnotě , kde a jsou limity vlevo a vpravo od bodu nespojitosti, resp.
Z průběhu matematické analýzy je také známo, že použití zkrácené Fourierovy řady, obsahující pouze první členy místo nekonečného součtu, vede k přibližné reprezentaci signálu:
Při které je zajištěna minimální střední kvadratická chyba. Obrázek 3 znázorňuje aproximaci periodického sledu obdélníkových vln a periodické rampové vlny při použití různých čísel členů Fourierovy řady.
Obrázek 3. Aproximace signálů pomocí zkrácené Fourierovy řady:
a - obdélníkové impulsy; b - pilový signál
Fourierovy řady v komplexní formě
V předchozí části jsme zkoumali trigonometrické Fourierovy řady pro expanzi libovolného periodického signálu splňujícího Dirichletovy podmínky. Pomocí Eulerova vzorce můžeme ukázat:
Potom trigonometrická Fourierova řada (2) s přihlédnutím k (4):
Periodický signál tedy může být reprezentován součtem konstantní složky a komplexních exponenciál rotujících na frekvencích s koeficienty pro kladné frekvence a pro komplexní exponenciály rotujících na záporných frekvencích.
Uvažujme koeficienty pro komplexní exponenciály rotující s kladnými frekvencemi:
Podobně koeficienty pro komplexní exponenciály rotující se zápornými frekvencemi jsou:
Výrazy (6) a (7) se navíc shodují, konstantní složku lze také zapsat pomocí komplexní exponenciály s nulovou frekvencí:
Takže (5) s přihlédnutím k (6)-(8) může být reprezentováno jako jeden součet při indexování od mínus nekonečna do nekonečna:
Z výrazu (2) vyplývá, že pro reálný signál jsou reálné i koeficienty řady (2). Nicméně (9) spojuje skutečný signál se sadou komplexně sdružených koeficientů souvisejících s pozitivními i negativními frekvencemi.
Některá vysvětlení Fourierovy řady v komplexní formě
V předchozí části jsme provedli přechod od trigonometrické Fourierovy řady (2) k Fourierově řadě v komplexní podobě (9). Výsledkem bylo, že místo rozkladu periodických signálů na bázi reálných goniometrických funkcí jsme obdrželi expanzi na bázi komplexních exponenciál, s komplexními koeficienty, a dokonce se v expanzi objevily i záporné frekvence! Vzhledem k tomu, že tato problematika je často nepochopena, je nutné určité objasnění.
Za prvé, práce s komplexními exponenty je ve většině případů jednodušší než práce s goniometrickými funkcemi. Například při násobení a dělení komplexních exponentů stačí exponenty pouze sčítat (odečítat), zatímco vzorce pro násobení a dělení goniometrických funkcí jsou těžkopádnější.
Derivování a integrace exponenciál, a to i komplexních, je také jednodušší než goniometrické funkce, které se při derivování a integraci neustále mění (sinus se mění na kosinus a naopak).
Pokud je signál periodický a reálný, pak se trigonometrická Fourierova řada (2) zdá jasnější, protože všechny expanzní koeficienty zůstávají reálné. Často se však musíme potýkat s komplexními periodickými signály (např. při modulaci a demodulaci se používá kvadraturní reprezentace komplexní obálky). V tomto případě se při použití trigonometrické Fourierovy řady všechny koeficienty a expanze (2) stanou komplexními, zatímco při použití Fourierovy řady v komplexním tvaru (9) budou použity stejné expanzní koeficienty pro reálné i komplexní vstupní signály. .
A nakonec je třeba se pozastavit nad vysvětlením negativních frekvencí, které se objevily v (9). Tato otázka často způsobuje nedorozumění. V Každodenní život se zápornými frekvencemi se nesetkáváme. Například nikdy neladíme naše rádio na zápornou frekvenci. Uvažujme následující analogii z mechaniky. Nechť existuje mechanické pružinové kyvadlo, které volně kmitá s určitou frekvencí. Může kyvadlo kmitat se zápornou frekvencí? Samozřejmě že ne. Stejně jako neexistují žádné rozhlasové stanice vysílající na záporných frekvencích, ani frekvence kmitů kyvadla nemůže být záporná. Ale pružinové kyvadlo je jednorozměrný objekt (kyvadlo kmitá podél jedné přímky).
Můžeme uvést i další přirovnání z mechaniky: kolo rotující s frekvencí . Kolo se na rozdíl od kyvadla otáčí, tzn. bod na povrchu kola se pohybuje v rovině a nekmitá pouze podél jedné přímky. Pro jednoznačné určení rotace kola tedy nestačí nastavení rychlosti rotace, protože je nutné nastavit i směr rotace. To je přesně důvod, proč můžeme použít frekvenční znak.
Pokud se tedy kolo otáčí s úhlovou frekvencí rad/s proti směru hodinových ručiček, pak uvažujeme, že se kolo otáčí s kladnou frekvencí, a pokud ve směru hodinových ručiček, pak bude frekvence otáčení záporná. Pro příkaz k rotaci tak záporná frekvence přestává být nesmyslem a udává směr rotace.
A teď to nejdůležitější, co musíme pochopit. Kmitání jednorozměrného předmětu (například pružinového kyvadla) lze znázornit jako součet rotací dvou vektorů znázorněných na obrázku 4.
Obrázek 4. Kývání pružinového kyvadla
jako součet rotací dvou vektorů
na komplexní rovině
Kyvadlo kmitá podél skutečné osy komplexní roviny s frekvencí podle harmonického zákona. Pohyb kyvadla je znázorněn jako horizontální vektor. Horní vektor rotuje v komplexní rovině s kladnou frekvencí (proti směru hodinových ručiček) a spodní vektor se otáčí se zápornou frekvencí (ve směru hodinových ručiček). Obrázek 4 jasně ilustruje dobře známý vztah z kurzu trigonometrie:
Fourierova řada v komplexní formě (9) tedy představuje periodické jednorozměrné signály jako součet vektorů v komplexní rovině rotujících s kladnými a zápornými frekvencemi. Zároveň si všimněme, že v případě reálného signálu podle (9) jsou expanzní koeficienty pro záporné frekvence komplexně sdružené s odpovídajícími koeficienty pro kladné frekvence. V případě komplexního signálu tato vlastnost koeficientů neplatí, protože a jsou také komplexní.
Spektrum periodických signálů
Fourierova řada v komplexní formě je rozklad periodického signálu na součet komplexních exponenciál rotujících na kladných a záporných frekvencích v násobcích rad/c s odpovídajícími komplexními koeficienty, které určují spektrum signálu. Komplexní koeficienty lze reprezentovat pomocí Eulerova vzorce jako , kde je amplitudové spektrum, a je fázové spektrum.
Protože periodické signály jsou uspořádány v řadě pouze na mřížce s pevnou frekvencí, je spektrum periodických signálů liniové (diskrétní).
Obrázek 5. Spektrum periodické sekvence
obdélníkové impulsy:
a - amplitudové spektrum; b - fázové spektrum
Obrázek 5 ukazuje příklad amplitudového a fázového spektra periodické sekvence pravoúhlých pulzů (viz obrázek 1) při c, trvání pulzu c a pulzní amplitudě B.
Fourierova řada periodických funkcí s periodou 2π.
Fourierova řada nám umožňuje studovat periodické funkce jejich rozkladem na složky. Typické jsou střídavé proudy a napětí, výchylky, rychlost a zrychlení klikových mechanismů a akustické vlny praktické příklady aplikace periodických funkcí v inženýrských výpočtech.
Rozšíření Fourierovy řady je založeno na předpokladu, že všechny funkce praktického významu v intervalu -π ≤x≤ π lze vyjádřit ve formě konvergentních goniometrických řad (řada je považována za konvergentní, jestliže posloupnost dílčích součtů složená z jejích členů konverguje):
Standardní (=obyčejný) zápis přes součet sinx a cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
kde a o, a 1,a 2,...,b 1,b 2,.. jsou reálné konstanty, tzn.
Kde pro rozsah od -π do π se koeficienty Fourierovy řady vypočítají pomocí vzorců:
Nazývají se koeficienty a o , a n a b n Fourierovy koeficienty a pokud je lze najít, zavolá se řada (1). vedle Fouriera, odpovídající funkci f(x). Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nazývá první resp základní harmonická,
Dalším způsobem, jak napsat řadu, je použít vztah acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Kde a o je konstanta, c 1 = (a 1 2 +b 1 2) 1/2, c n = (a n 2 +b n 2) 1/2 jsou amplitudy různých složek a rovná se a n =arctg a n /b n.
Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nebo c 1 sin(x+α 1) nazývá první resp. základní harmonická,(a 2 cos2x+b 2 sin2x) nebo c 2 sin(2x+α 2) se nazývá druhá harmonická a tak dále.
Přesná reprezentace komplexního signálu obvykle vyžaduje nekonečný počet termínů. V mnoha praktických problémech však stačí vzít v úvahu pouze prvních několik termínů.
Fourierova řada neperiodických funkcí s periodou 2π.
Rozšíření neperiodických funkcí.
Pokud je funkce f(x) neperiodická, znamená to, že ji nelze rozšířit do Fourierovy řady pro všechny hodnoty x. Je však možné definovat Fourierovu řadu reprezentující funkci v libovolném rozsahu šířky 2π.
Vzhledem k neperiodické funkci lze novou funkci zkonstruovat výběrem hodnot f(x) v určitém rozsahu a jejich opakováním mimo tento rozsah v intervalech 2π. Protože je nová funkce periodická s periodou 2π, lze ji rozšířit do Fourierovy řady pro všechny hodnoty x. Například funkce f(x)=x není periodická. Pokud je však nutné ji rozšířit na Fourierovu řadu v intervalu od o do 2π, pak se mimo tento interval sestrojí periodická funkce s periodou 2π (jak je znázorněno na obrázku níže).
Pro neperiodické funkce, jako je f(x)=x, se součet Fourierovy řady rovná hodnotě f(x) ve všech bodech v daném rozsahu, ale u bodů se nerovná f(x). mimo rozsah. K nalezení Fourierovy řady neperiodické funkce v rozsahu 2π se používá stejný vzorec Fourierových koeficientů.
Sudé a liché funkce.
Říkají, že funkce y=f(x) dokonce, pokud f(-x)=f(x) pro všechny hodnoty x. Grafy sudých funkcí jsou vždy symetrické podle osy y (tj. jsou to zrcadlové obrazy). Dva příklady sudých funkcí: y=x2 a y=cosx.
Říká se, že funkce y=f(x) zvláštní, jestliže f(-x)=-f(x) pro všechny hodnoty x. Grafy lichých funkcí jsou vždy symetrické podle počátku.
Mnoho funkcí není ani sudých, ani lichých.
Expanze Fourierovy řady v kosinech.
Fourierova řada sudé periodické funkce f(x) s periodou 2π obsahuje pouze kosinové členy (tj. žádné sinusové členy) a může zahrnovat konstantní člen. Proto,
kde jsou koeficienty Fourierovy řady,
Fourierova řada liché periodické funkce f(x) s periodou 2π obsahuje pouze členy se siny (tj. neobsahuje členy s kosiny).
Proto,
kde jsou koeficienty Fourierovy řady,
Fourierova řada v půlcyklu.
Pokud je funkce definována pro rozsah, řekněme od 0 do π, a nikoli pouze od 0 do 2π, lze ji v řadě rozšířit pouze v sinech nebo pouze v kosinech. Výsledná Fourierova řada se nazývá poblíž Fouriera v polovičním cyklu.
Pokud chcete získat rozklad Půlcyklus Fourier podle kosinu funkce f(x) v rozsahu od 0 do π, pak je nutné sestrojit sudou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože dokonce funkce symetricky podle osy f(x) nakreslete čáru AB, jak je znázorněno na obr. níže. Pokud předpokládáme, že mimo uvažovaný interval získaná trojúhelníkový tvar je periodický s periodou 2π, výsledný graf pak vypadá, ukaž. na Obr. níže. Protože potřebujeme získat Fourierovu expanzi v kosinech, jako dříve, vypočítáme Fourierovy koeficienty a o a a n
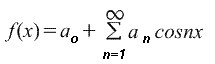
Pokud potřebujete získat Fourierova půlcyklová sinusová expanze funkce f(x) v rozsahu od 0 do π, pak je nutné sestrojit lichou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože lichá funkce je symetrická k počátku, sestrojíme úsečku CD, jak je znázorněno na obr. Předpokládáme-li, že mimo uvažovaný interval je výsledný pilový signál periodický s periodou 2π, pak má výsledný graf tvar znázorněný na Obr. Protože potřebujeme získat Fourierovu expanzi polocyklu v sinech, jako dříve, vypočítáme Fourierův koeficient. b
Fourierova řada pro libovolný interval.
Rozšíření periodické funkce s periodou L.
Periodická funkce f(x) se opakuje, když se x zvyšuje o L, tj. f(x+L)=f(x). Přechod od dříve uvažovaných funkcí s periodou 2π k funkcím s periodou L je poměrně jednoduchý, protože jej lze provést pomocí změny proměnné.
Abychom našli Fourierovu řadu funkce f(x) v rozsahu -L/2≤x≤L/2, zavedeme novou proměnnou u, takže funkce f(x) má vůči u periodu 2π. Jestliže u=2πx/L, pak x=-L/2 pro u=-π a x=L/2 pro u=π. Nechť také f(x)=f(Lu/2π)=F(u). Fourierova řada F(u) má tvar
(Meze integrace lze nahradit libovolným intervalem délky L, například od 0 do L)
Fourierova řada na půlcyklu pro funkce zadané v intervalu L≠2π.
Pro substituci u=πх/L interval od x=0 do x=L odpovídá intervalu od u=0 do u=π. Funkce může být následně rozšířena do řady pouze v kosinech nebo pouze v sinech, tzn. PROTI Fourierova řada v půlcyklu.
Kosinusová expanze v rozsahu od 0 do L má tvar
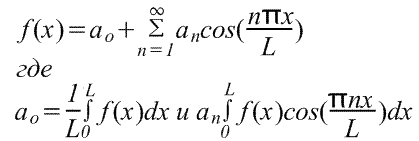
, Kde
.
Fourierova řada funkce f(x) na intervalu (-l;l) je trigonometrická řada ve tvaru: 
, Kde
.
Účel. Online kalkulačka je navržen tak, aby rozšířil funkci f(x) do Fourierovy řady.
Pro modulo funkce (jako |x|) použijte kosinusová expanze.
Pravidla pro zadávání funkcí:
Pro modulo funkce použijte kosinusovou expanzi. Například pro |x| je nutné zadat funkci bez modulu, tzn. X.Fourierova řada po částech spojitá, po částech monotónní a ohraničená intervalem (- l;l) funkce konverguje na celé číselné ose.
Součet Fourierovy řady S(x) :
- je periodická funkce s periodou 2 l. Funkce u(x) se nazývá periodická s periodou T (nebo T-periodická), jestliže pro všechna x oblasti R platí u(x+T)=u(x).
- na intervalu (- l;l) se shoduje s funkcí F(X), kromě bodů přerušení
- v bodech nespojitosti (prvního druhu, protože funkce je omezená) funkce F(X) a na konci intervalu nabývá průměrných hodnot:
Říká se, že funkce expanduje do Fourierovy řady na intervalu (- l;l):
.
Li F(X) je sudá funkce, pak se na jejím rozšíření podílejí pouze sudé funkce, tzn b n=0.
Li F(X) je lichá funkce, pak se na jejím rozšíření podílejí pouze liché funkce, tzn a n=0
Blízko Fouriera
funkcí F(X) na intervalu (0; l) kosinusem více oblouků
řádek se jmenuje: 
, Kde 
.
Blízko Fouriera
funkcí F(X) na intervalu (0; l) podél sinů více oblouků
řádek se jmenuje: 
, Kde 
.
Součet Fourierovy řady přes kosinus více oblouků je sudá periodická funkce s periodou 2 l, shodující se s F(X) na intervalu (0; l) v bodech spojitosti.
Součet Fourierovy řady přes siny více oblouků je lichá periodická funkce s periodou 2 l, shodující se s F(X) na intervalu (0; l) v bodech spojitosti.
Fourierova řada pro danou funkci na daném intervalu má vlastnost jednoznačnosti, to znamená, že pokud je expanze získána jiným způsobem než pomocí vzorců, například výběrem koeficientů, pak se tyto koeficienty shodují s koeficienty vypočtenými ze vzorců .
Příklad č. 1. Rozbalit funkci f(X)=1:
a) v úplné Fourierově řadě na intervalu(-π ;π);
b) v řadě podél sinů více oblouků na intervalu(0;π); vyneste výslednou Fourierovu řadu
Řešení:
a) Rozšíření Fourierovy řady na intervalu (-π;π) má tvar: 
,
a všechny koeficienty b n=0, protože tato funkce je sudá; Tím pádem,
Je zřejmé, že pokud přijmeme, rovnost bude splněna
A 0 =2, A 1 =A 2 =A 3 =…=0
Vzhledem k vlastnosti jedinečnosti se jedná o požadované koeficienty. Požadovaný rozklad tedy: 
nebo jen 1=1.
V tomto případě, kdy se řada shodně shoduje se svou funkcí, se graf Fourierovy řady shoduje s grafem funkce na celé číselné ose.
b) Rozšíření na intervalu (0;π) z hlediska sinů více oblouků má tvar:
Je zjevně nemožné vybrat koeficienty tak, aby rovnost platila shodně. Pro výpočet koeficientů použijeme vzorec:
Tedy pro dokonce n (n=2k) my máme b n=0, pro liché ( n=2k-1) - 
Konečně, 
.
Výslednou Fourierovu řadu vyneseme pomocí jejích vlastností (viz výše).
Nejprve sestrojíme graf této funkce na daném intervalu. Dále, s využitím lichosti součtu řady, pokračujeme v grafu symetricky k počátku: 
Pokračujeme periodickým způsobem podél celé číselné řady: 
A nakonec v bodech přerušení vyplníme průměrné (mezi pravou a levou hranicí) hodnoty: 
Příklad č. 2. Rozbalte funkci 
na intervalu (0;6) podél sinů více oblouků.
Řešení: Požadované rozšíření má tvar:
Protože jak levá, tak pravá strana rovnosti obsahují pouze funkce hřích z různých argumentů byste měli zkontrolovat, zda pro všechny hodnoty n (přirozené!) argumenty sinů v levém a pravé části rovnost:
nebo , z nichž n = 18. To znamená, že takový člen je obsažen na pravé straně a jeho koeficient se musí shodovat s koeficientem na levé straně: b 18 =1;
nebo , z nichž n = 4. Prostředek, b 4 =-5.
Takže výběrem koeficientů bylo možné získat požadovanou expanzi:
Federální státní rozpočet vzdělávací instituce vysokoškolské vzdělání
„STÁTNÍ UNIVERZITA VOLHA
TELEKOMUNIKACE A INFORMATIKA"
Katedra vyšší matematiky
O.V.STAROZHILOVA
SPECIÁLNÍ KAPITOLY MATEMATICKÉHO VĚTU
protokol č. 45, ze dne 10.3.2017
Starožilová, O.V.
C Speciální kapitoly matematiky: učebnice //Starozhilova O.V.. – Samara: PGUTI, 2017. –221 s.
Tutorial dotýká se speciálních oborů matematiky: matematická logika a teorie automatů, výroková algebra, výrokový počet, prvky teorie algoritmů, regresní analýza, optimalizační metody.
Pro studenty vysokých škol a magisterské studium ve směru 03/09/02 " Informační systémy a technologie“, kteří chtějí samostatně studovat speciální kapitoly matematiky.
Každá část je zakončena kontrolními otázkami, které pomohou ověřit teoretické zvládnutí předmětu, obsahuje velké množství úkolů pro nezávislé rozhodnutí a odpovědi ke kontrole.
Příručka obsahuje laboratorní komplex a řadu inženýrských problémů s důrazem na softwarovou implementaci metod výpočetní matematiky.
Starozhilova O.V., 2017
Kapitola 1 Harmonická analýza 6
1.1 Problém se znějící strunou 7
1.2 Ortogonální systémy funkcí 8
1.3 Fourierovy řady pro goniometrický systém funkcí 10
1.4 Dostatečné podmínky rozšíření funkce ve Fourierově řadě 13
1.5 Rozšíření Fourierovy řady neperiodické funkce 17
1.6 Fourierova řada pro sudé a liché funkce 18
1.7 Fourierovy řady pro funkce libovolné periody 21
1.8 Fourierův integrál 27
1.9 Fourierův integrál pro sudé a liché funkce 29
1.10 Složitá forma Fourierův integrál 30
1.11 Fourierova transformace 32
Kapitola 2 Matematická logika a IV 33
2.1 Fáze vývoje logiky 34
2.2 Výroková logika 38
2.3Logické spojky 40
2.4Logické operace 41
2.5 Abeceda výrokového počtu 42
2.6 Vzorce 42
2.7 Zákony výrokové logiky 44
2.8 Formální teorie. Líhnivost. Výklad 46
2.9 Axiomatická metoda 47
2.10 Systém axiomů výrokového počtu (PS) 52
2.11 Pravidla závěru 53
2.12 Odvozená pravidla odvození 56
2.13 Konstrukce závěru ve výrokové logice 62
2.14 Vztah mezi algebrou a výrokovým počtem 66
Kapitola 3 Problémy regresní analýzy 70
3.1 Metoda nejmenší čtverce 74
3.2 Lineární regresní analýza 76
3.3 Odhad regresního modelu 79
3.4 Problémy při aplikaci metody lineární regrese 83
3.5 Předpoklady statistického modelu LR 85
3.6 Problémy regresní analýzy 86
3.7 Vícerozměrný normální regresní model 90
3.8 Variace závislé proměnné 92
Testové otázky 94
Kapitola 4 Obecná formulace a typy rozhodovacích problémů 95
4.1 Matematická formulace optimalizační úlohy 97
4.2 Místní a globální minimum TF 99
4.3 Metody bezpodmínečná optimalizace 102
4.4 Metoda sestupu souřadnic 102
4.5 Rosenbrockova metoda 105
4.6 Způsob konfigurace 105
4.7 Metody náhodného vyhledávání 108
4.8 Newtonova metoda 112
Kapitola 5 Fourierova transformace 114
5.1 Aproximace Fourierovy funkce 114
5.2 Fourierova transformace 117
5.3 Rychlá Fourierova transformace 120
LABORATORNÍ KOMPLEX 123
Harmonická a spektrální analýza 123
Téma 1. „Výroková logika“ 131
Varianty jednotlivých zadání k tématu LP 133
Téma 2. Lineární párová regrese 140
Laboratorní práce № 1 141
Výpočet koeficientů LR rovnice 141
Laboratorní práce č. 2 144
Výpočet výběrového korelačního koeficientu 144
Laboratorní práce č. 3 145
Výpočet odhadů rozptylů párových LR 145
Laboratorní práce č. 4 147
Excel funkce pro párové LR koeficienty 147
Laboratorní práce č. 5 149
Konstrukce intervalového odhadu pro párovou LR funkci 149
Laboratorní práce č. 6 151
Kontrola významnosti LR rovnice pomocí Fisherova kritéria 151
Téma 3 Nelineární párová regrese 153
Laboratorní práce č. 7 153
Vytvoření nelineární regrese pomocí 153
Přidat příkazy spojnice trendu 153
Laboratorní práce č. 8 158
Výběr nejlepší nelineární regrese 158
Téma 4. Lineární vícenásobná regrese 161
Laboratorní práce č. 9 162
Výpočet koeficientů LMR 162
Laboratorní práce č. 10 166
Testování významnosti v regresním režimu 166
Téma 5. Nelineární vícenásobná regrese 175
Laboratorní práce č. 11 175
Výpočet pro Cobb-Douglasovu funkci 175
Test № 1 179
Párová regrese 179
Test č. 2 181
Množný lineární regrese 181
Numerické metody pro hledání nepodmíněného extrému 185
Grafická analýza funkce 185
Problém jednorozměrného vyhledávání 187
Svennův algoritmus 190
Metoda hrubé síly 193
Bitová metoda vyhledávání 195
Metoda dichotomie. 198
Fibonacciho metoda 201
Metoda zlatého řezu 205
Metoda středního bodu 210
Newtonova metoda 214
Literatura 218
Kapitola 1 Harmonická analýza
DefiniceHarmonická analýza - obor matematiky spojený s rozkladem vibrací na harmonické vibrace.
Při studiu periodických (tj. opakujících se v čase) jevů uvažujeme periodické funkce.
Například harmonické kmitání je popsáno periodickou funkcí času t:
Ø DefinicePeriodická funkce- funkce, jejíž hodnota se při volání určitého nenulového čísla nemění doba funkcí.
Vzhledem k tomu, že součet a rozdíl dvou period je opět periodou, a tudíž i libovolný násobek periody je periodou, pak má každá periodická funkce nekonečný počet period.
Pokud má periodická funkce reálnou periodu, je spojitá a odlišná od konstanty, pak má nejmenší kladnou periodu T; jakákoli jiná reálná perioda stejné funkce bude mít tvar kT, Kde k =±1, ±2,....
Součet, součin a podíl periodických funkcí se stejnou periodou jsou periodické funkce se stejnou periodou.
Periodické funkce hrají mimořádně důležitou roli v teorii kmitů a v matematické fyzice obecně. V průběhu matematické analýzy jsme se seznámili s pojmem funkční řady, pracovali jsme s jejím důležitým speciálním případem - mocninná řada. Podívejme se na další velmi důležitý (včetně fyzických aplikací) speciální případ funkční řada - trigonometrické řady.
Ø Definice Funkční rozsah -řada formuláře
kde jsou funkce závislé na jedné proměnné nebo několika proměnných.
Pro každou pevnou hodnotu se funkční řada změní na číselnou řadu
které se mohou sbíhat nebo se mohou rozcházet.
Ø Definice Bod konvergence funkčních řad- bod, ve kterém funkční řada konverguje.
Ø Definice Množina všech bodů konvergence se nazývá oblast konvergence řady.
je to možné tuto funkci reprezentovat ve formě trigonometrické řady, tzn. je možné najít koeficienty? a n A b n tak, aby byla pro všechny rovnost
Součet řady je zjevně periodická funkce. To znamená, že pouze periodické funkce mohou být rozšířeny do goniometrické řady F.
Navíc je jasné, že pokud se dvě periodické funkce shodují na intervalu, jehož délka je rovna periodě, pak se shodují všude. Stačí tedy zkontrolovat na určitém intervalu délky, např. .
1.1 Problém se znějící strunou
Ke studiu trigonometrických řad vedl problém se znějící strunou položený v 18. století.
Je možné za dané funkce najít goniometrickou řadu, která konverguje a má jako součet funkci. Je nutné na ni uvalit omezení, aby bylo možné hledat trigonometrické řady k ní konvergující.
Podobný úkol byl pro mocninná řada, pokud je řešitelná, pak je taková řada Taylorova řada.
1.2 Ortogonální systémy funkcí
Systematické studium ortogonálních systémů funkcí bylo zahájeno v souvislosti s Fourierovou metodou pro řešení okrajových úloh rovnic matematické fyziky. Jedním z hlavních problémů teorie ortogonálních systémů funkcí je problém rozkladu funkce F(X) v řadě tvaru , kde je ortogonální systém funkcí.
Ø Definice Funkce jsou volány ortogonální dne , pokud je splněno:
q Příklad , 
- funkce jsou ortogonální k , protože 
q Příklad on je ortogonální k jakékoli funkci definované na.
Ø Definice Nazývá se nekonečný systém funkcí ortogonální na pokud
q Příklad Nekonečný systém funkcí netvoří ortogonální systém funkcí
q Příklad -trigonometrický funkční systém tvoří k němu ortogonální systém funkcí.
, 
, 
.
Ø Definice Nechť libovolný systém funkcí ortogonální k . Řádek
kde jsou libovolné číselné koeficienty, tzv vedle sebe podle ortogonálního systému funkcí.
Ø DefiniceŘady podle goniometrické soustavy funkcí
volal trigonometrická řada.
ü Komentář Jestliže je součet goniometrických řad konvergujících v každém bodě, pak je periodický, protože , jsou periodické funkce s periodou, pak v rovnosti 
nic se nezmění, proto pravidelně.
ü Komentář Pokud je na segmentu uvedeno, ale ne , pak posunutím počátku souřadnic může být redukováno na studovaný případ.
ü Komentář Jestliže periodická funkce s periodou není , pak se rozšíří do trigonometrické řady
q Teorém Konverguje-li číselná řada, pak řada goniometrická
sbíhá absolutně a rovnoměrně podél celé osy.
Důkaz
Proto,
řada - majorizuje danou goniometrickou řadu a podle Weierstrassova testu rovnoměrně konverguje.
Absolutní konvergence je zřejmá.
1.3 Fourierovy řady pro goniometrický systém funkcí
Jean Baptiste Joseph Fourier 1768 – 1830 – francouzský matematik.
Pro výpočet koeficientů Fourierovy řady počítáme integrály
, 
, 
, 
,
q Teorém Pokud existuje rovnost pro všechny
a trigonometrická řada konverguje rovnoměrně na celé ose, pak se určí koeficienty této řady
, 
,
Důkaz
Řada konverguje rovnoměrně na celé číselné ose, její členy jsou spojité funkce, pak je spojitý i její součet a integrace řady po členech je možná v rámci
Každý integrál je roven nule, protože trigonometrický systém funkcí je ortogonální k , a pak
Chcete-li to dokázat, vynásobte obě strany
Tím se nenaruší rovnoměrná konvergence řady.
Kvůli rovnoměrné konvergenci řady
a to znamená rovnoměrnou konvergenci řady.
Integrace na , máme
Vzhledem k ortogonalitě trigonometrické soustavy funkcí na
, 
a od 
integrál v ,
, to atd.
Připomeňme si to
Platnost těchto rovností vyplývá z aplikace goniometrických vzorců na integrand.
Vzorec pro je dokázán podobným způsobem.
ü Komentář Věta zůstává platná pro jakýkoli interval a limity integrace jsou nahrazeny a resp.
Ø Definice Trigonometrické řady
,
jejichž koeficienty jsou určeny vzorci
, ,
,
volal vedle Fouriera pro funkci a jsou volány koeficienty Fourierovy koeficienty.
Pokud Fourierova řada funkce f(x) konverguje ve všech svých bodech spojitosti, pak říkáme, že funkce f(x) je rozšířena do Fourierovy řady.
ü Komentář Ne každá trigonometrická řada je Fourierova řada, i když konverguje na celé číselné ose.
Součet nestejnoměrně konvergentních řad může být nespojitý a neintegrovatelný, takže určení Fourierových koeficientů je nemožné.
ü Komentář Fourierova řada je speciální případ funkčních řad.
1.4 Dostatečné podmínky pro rozvoj funkce ve Fourierově řadě
Ø Definice Funkce je volána po částech monotónní v segmentu, pokud lze tento segment vydělit konečným počtem bodů x 1, x 2, ..., x n-1 do intervalů ( A,x 1), (x 1,x 2), ..., (xn-1,b), takže na každém z intervalů je funkce monotónní, to znamená, že se buď nezvyšuje, nebo neklesá.
ü Komentář Z definice vyplývá, že pokud je funkce po částech monotónní a omezená na [ A,b], pak má pouze diskontinuity prvního druhu.
Ø Definice Funkce je volána po částech hladké, jestliže na každém konečném intervalu má on a jeho derivace nejvýše konečný počet bodů nespojitosti 1. druhu.
q Věta (Dirichletova podmínka postačující podmínka pro rozložitelnost funkce ve Fourierově řadě): Pokud periodická funkce s periodou splňuje jednu z podmínek:
pak Fourierova řada konstruovaná pro tuto funkci konverguje ve všech bodech
a konverguje k číslu 
v každém bodě jeho diskontinuity.
Součet výsledné řady je roven hodnotě funkce v bodech spojitosti funkce
Funkce, jejich rozklad na komponenty. Střídavé proudy a napětí, výchylky, rychlost a zrychlení klikových mechanismů a akustické vlny jsou typickými praktickými příklady využití periodických funkcí v inženýrských výpočtech.
Rozšíření Fourierovy řady je založeno na předpokladu, že všechny funkce praktického významu v intervalu -π ≤x≤ π lze vyjádřit ve formě konvergentních goniometrických řad (řada je považována za konvergentní, jestliže posloupnost dílčích součtů složená z jejích členů konverguje):
Standardní (=obyčejný) zápis přes součet sinx a cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
kde a o, a 1,a 2,...,b 1,b 2,.. jsou reálné konstanty, tzn.
Kde pro rozsah od -π do π se koeficienty Fourierovy řady vypočítají pomocí vzorců:
Nazývají se koeficienty a o , a n a b n Fourierovy koeficienty a pokud je lze najít, zavolá se řada (1). vedle Fouriera, odpovídající funkci f(x). Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nazývá první resp základní harmonická,
Dalším způsobem, jak napsat řadu, je použít vztah acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Kde a o je konstanta, c 1 = (a 1 2 +b 1 2) 1/2, c n = (a n 2 +b n 2) 1/2 jsou amplitudy různých složek a rovná se a n =arctg a n /b n.
Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nebo c 1 sin(x+α 1) nazývá první resp. základní harmonická,(a 2 cos2x+b 2 sin2x) nebo c 2 sin(2x+α 2) se nazývá druhá harmonická a tak dále.
Přesná reprezentace komplexního signálu obvykle vyžaduje nekonečný počet termínů. V mnoha praktických problémech však stačí vzít v úvahu pouze prvních několik termínů.
Fourierova řada neperiodických funkcí s periodou 2π.
Rozšíření neperiodických funkcí do Fourierových řad.
Pokud je funkce f(x) neperiodická, znamená to, že ji nelze rozšířit do Fourierovy řady pro všechny hodnoty x. Je však možné definovat Fourierovu řadu reprezentující funkci v libovolném rozsahu šířky 2π.
Vzhledem k neperiodické funkci lze novou funkci zkonstruovat výběrem hodnot f(x) v určitém rozsahu a jejich opakováním mimo tento rozsah v intervalech 2π. Protože je nová funkce periodická s periodou 2π, lze ji rozšířit do Fourierovy řady pro všechny hodnoty x. Například funkce f(x)=x není periodická. Pokud je však nutné ji rozšířit na Fourierovu řadu v intervalu od o do 2π, pak se mimo tento interval sestrojí periodická funkce s periodou 2π (jak je znázorněno na obrázku níže).
Pro neperiodické funkce, jako je f(x)=x, se součet Fourierovy řady rovná hodnotě f(x) ve všech bodech v daném rozsahu, ale u bodů se nerovná f(x). mimo rozsah. K nalezení Fourierovy řady neperiodické funkce v rozsahu 2π se používá stejný vzorec Fourierových koeficientů.
Sudé a liché funkce.
Říkají, že funkce y=f(x) dokonce, pokud f(-x)=f(x) pro všechny hodnoty x. Grafy sudých funkcí jsou vždy symetrické podle osy y (tj. jsou to zrcadlové obrazy). Dva příklady sudých funkcí: y=x2 a y=cosx.
Říká se, že funkce y=f(x) zvláštní, jestliže f(-x)=-f(x) pro všechny hodnoty x. Grafy lichých funkcí jsou vždy symetrické podle počátku.
Mnoho funkcí není ani sudých, ani lichých.
Expanze Fourierovy řady v kosinech.
Fourierova řada sudé periodické funkce f(x) s periodou 2π obsahuje pouze kosinové členy (tj. žádné sinusové členy) a může zahrnovat konstantní člen. Proto,
kde jsou koeficienty Fourierovy řady,
Fourierova řada liché periodické funkce f(x) s periodou 2π obsahuje pouze členy se siny (tj. neobsahuje členy s kosiny).
Proto,
kde jsou koeficienty Fourierovy řady,
Fourierova řada v půlcyklu.
Pokud je funkce definována pro rozsah, řekněme od 0 do π, a nikoli pouze od 0 do 2π, lze ji v řadě rozšířit pouze v sinech nebo pouze v kosinech. Výsledná Fourierova řada se nazývá poblíž Fouriera v polovičním cyklu.
Pokud chcete získat rozklad Půlcyklus Fourier podle kosinu funkce f(x) v rozsahu od 0 do π, pak je nutné sestrojit sudou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože sudá funkce je symetrická kolem osy f(x), nakreslíme přímku AB, jak je znázorněno na Obr. níže. Pokud předpokládáme, že mimo uvažovaný interval je výsledný trojúhelníkový tvar periodický s periodou 2π, pak výsledný graf vypadá takto: na Obr. níže. Protože potřebujeme získat Fourierovu expanzi v kosinech, jako dříve, vypočítáme Fourierovy koeficienty a o a a n
Pokud chcete získat funkce f(x) v rozsahu od 0 do π, musíte sestrojit lichou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože lichá funkce je symetrická k počátku, sestrojíme úsečku CD, jak je znázorněno na obr. Předpokládáme-li, že mimo uvažovaný interval je výsledný pilový signál periodický s periodou 2π, pak má výsledný graf tvar znázorněný na Obr. Protože potřebujeme získat Fourierovu expanzi polocyklu v sinech, jako dříve, vypočítáme Fourierův koeficient. b
Fourierova řada pro libovolný interval.
Rozšíření periodické funkce s periodou L.
Periodická funkce f(x) se opakuje, když se x zvětšuje o L, tzn. f(x+L)=f(x). Přechod od dříve uvažovaných funkcí s periodou 2π k funkcím s periodou L je poměrně jednoduchý, protože jej lze provést pomocí změny proměnné.
Abychom našli Fourierovu řadu funkce f(x) v rozsahu -L/2≤x≤L/2, zavedeme novou proměnnou u, takže funkce f(x) má vůči u periodu 2π. Jestliže u=2πx/L, pak x=-L/2 pro u=-π a x=L/2 pro u=π. Nechť také f(x)=f(Lu/2π)=F(u). Fourierova řada F(u) má tvar
Kde jsou koeficienty Fourierovy řady,
Častěji však výše uvedený vzorec vede k závislosti na x. Protože u=2πx/L, znamená to du=(2π/L)dx a limity integrace jsou od -L/2 do L/2 místo - π do π. V důsledku toho má Fourierova řada pro závislost na x tvar
kde v rozsahu od -L/2 do L/2 jsou koeficienty Fourierovy řady,
(Meze integrace lze nahradit libovolným intervalem délky L, například od 0 do L)
Fourierova řada na půlcyklu pro funkce zadané v intervalu L≠2π.
Pro substituci u=πх/L interval od x=0 do x=L odpovídá intervalu od u=0 do u=π. Funkce může být následně rozšířena do řady pouze v kosinech nebo pouze v sinech, tzn. PROTI Fourierova řada v půlcyklu.
Kosinusová expanze v rozsahu od 0 do L má tvar
