Domov Bolest zubu Rozšíření periodické funkce do trigonometrické Fourierovy řady. Expanze Fourierovy řady v kosinech

Bolest zubu

Rozšíření periodické funkce do trigonometrické Fourierovy řady. Expanze Fourierovy řady v kosinech

Které už jsou docela nudné. A cítím, že nastala chvíle, kdy je čas vytěžit ze strategických rezerv teorie nové konzervy. Je možné funkci rozšířit do série nějakým jiným způsobem? Vyjádřete například úsečku v podobě sinus a kosinus? Zdá se to neuvěřitelné, ale takové zdánlivě vzdálené funkce mohou být
"shledání". Kromě známých titulů v teorii a praxi existují další přístupy k rozšíření funkce do řady.

V této lekci se naučíme o trigonometrii. vedle Fouriera, dotkneme se problematiky její konvergence a součtu a samozřejmě rozebereme četné příklady expanze funkcí ve Fourierově řadě. Upřímně jsem chtěl článek nazvat „Fourierovy řady pro figuríny“, ale bylo by to nefér, protože řešení problémů by vyžadovalo znalost jiných odvětví matematické analýzy a určité praktické zkušenosti. Proto bude preambule připomínat výcvik astronautů =)

Za prvé, měli byste přistupovat ke studiu materiálů stránky ve vynikající formě. Ospalý, odpočatý a střízlivý. Bez silných emocí o zlomené křeččí tlapce a obsedantní myšlenky o útrapách života akvarijní ryby. Fourierovy řady však není těžké pochopit praktické úkoly prostě vyžadují zvýšenou koncentraci pozornosti – v ideálním případě byste se měli zcela odpoutat od vnějších podnětů. Situaci zhoršuje fakt, že neexistuje jednoduchý způsob, jak si řešení a odpověď ověřit. Pokud je tedy vaše zdraví podprůměrné, je lepší udělat něco jednoduššího. Je to pravda.

Za druhé, před letem do vesmíru si musíte prostudovat přístrojovou desku kosmická loď. Začněme hodnotami funkcí, na které je třeba na stroji kliknout:

Pro jakoukoli přírodní hodnotu:

1). Ve skutečnosti sinusoida „prošívá“ osu x každým „pí“:
. V případě záporných hodnot argumentu bude výsledek samozřejmě stejný: .

2). Ale ne každý to věděl. Kosinus „pí“ je ekvivalentem „blikače“:

Negativní argument na věci nic nemění: .

Snad to stačí.

A za třetí, milý kosmonautský sbor, musíte být schopni... integrovat se.
Zejména s jistotou zahrnout funkci pod diferenciální znaménko, integrovat po částech a být v souladu s Newton-Leibnizovým vzorcem. Začněme důležitá předletová cvičení. Kategoricky nedoporučuji přeskakovat, abych se později nezmačkal ve stavu beztíže:

Příklad 1

Vypočítejte určité integrály

kde nabývá přírodních hodnot.

Řešení: integrace se provádí přes proměnnou „x“ a v této fázi je diskrétní proměnná „en“ považována za konstantu. Ve všech integrálech přiřadíme funkci pod diferenciální znaménko:

Krátká verze řešení, na kterou by bylo dobré cílit, vypadá takto:

Pojďme si zvyknout:

Zbývající čtyři body jsou na vás. Pokuste se k úkolu přistupovat svědomitě a integrály pište stručně. Ukázky řešení na konci lekce.

Po provedení cviků KVALITA oblékáme skafandry
a připravte se na start!

Rozšíření funkce do Fourierovy řady na intervalu

Uvažujme nějakou funkci, která je definována alespoň na intervalu (a případně na větším intervalu). Pokud je tato funkce integrovatelná na intervalu, lze ji rozšířit na trigonometrické Fourierovy řady:
, kde jsou tzv Fourierovy koeficienty.

V tomto případě se číslo nazývá perioda rozkladu a číslo se nazývá půlperioda rozkladu.

Je zřejmé, že v obecném případě se Fourierova řada skládá ze sinů a kosinů:

Opravdu, pojďme to napsat podrobně:

Nultý člen řady se obvykle zapisuje ve tvaru .

Fourierovy koeficienty se vypočítají pomocí následujících vzorců:

Dobře chápu, že těm, kdo začínají toto téma studovat, stále nejsou jasné nové termíny: období rozkladu, poloviční cyklus, Fourierovy koeficienty atd. Nepanikařte, to se nedá srovnat s vzrušením před odletem do vesmíru. Pochopme vše v následujícím příkladu, před jeho provedením je logické položit naléhavé praktické otázky:

Co musíte udělat v následujících úkolech?

Rozšiřte funkci do Fourierovy řady. Navíc je často nutné zobrazit graf funkce, graf součtu řady, částečného součtu a v případě sofistikovaných profesorských fantazií udělat něco jiného.

Jak rozšířit funkci do Fourierovy řady?

V podstatě musíte najít Fourierovy koeficienty, tedy sestavit a vypočítat tři určité integrály.

Zkopírujte si prosím obecný tvar Fourierovy řady a tři pracovní vzorce do svého poznámkového bloku. Jsem velmi rád, že někteří návštěvníci stránek realizují svůj dětský sen stát se astronautem přímo před mýma očima =)

Příklad 2

Rozšiřte funkci do Fourierovy řady na intervalu. Sestrojte graf, graf součtu řady a dílčího součtu.

Řešení: První částí úlohy je rozšířit funkci do Fourierovy řady.

Začátek je standardní, nezapomeňte si zapsat, že:

V tomto problému je období expanze poloviční.

Rozšiřme funkci na Fourierovu řadu na intervalu:

Pomocí příslušných vzorců najdeme Fourierovy koeficienty. Nyní musíte sestavit a vypočítat tři určité integrály. Pro usnadnění očísluji body:

1) První integrál je nejjednodušší, ale vyžaduje také oční bulvy:

2) Použijte druhý vzorec:

Tento integrál je dobře známý a skládá se z částí:

Při hledání byla použita metoda subsumování funkce pod diferenciální znaménko.

V uvažované úloze je výhodnější okamžitě použít vzorec pro integraci po částech v určitém integrálu :

Pár technických poznámek. Za prvé, po použití vzorce musí být celý výraz uzavřen do velkých závorek, protože před původním integrálem je konstanta. Ať ji neztratíme! Závorky lze rozšířit v jakémkoli dalším kroku. Udělal jsem to jako poslední možnost. V prvním "kusu" Při substituci projevujeme extrémní péči, jak vidíte, konstanta se nepoužívá a do produktu se dosazují meze integrace. Tato akce je zvýrazněna v hranatých závorkách. Integrál druhého „kusu“ vzorce znáte z tréninkového úkolu ;-)

A hlavně – maximální koncentrace!

3) Hledáme třetí Fourierův koeficient:

Získá se relativní vztah k předchozímu integrálu, který lze také integrovat po částech:

Tento případ je trochu složitější, další kroky okomentuji krok za krokem:

(1) Celý výraz uzavíráme do velkých závorek. Nechtěl jsem vypadat nudně, příliš často ztrácejí konstantu.

(2) V v tomto případě Okamžitě jsem otevřel ty velké závorky. Speciální pozornost Věnujeme se prvnímu „kousku“: konstanta kouří stranou a nepodílí se na nahrazování mezí integrace (a ) do produktu. Vzhledem k nepřehlednosti nahrávky je opět vhodné tento úkon zvýraznit hranatými závorkami. S druhým "kusem" vše je jednodušší: zde se zlomek objevil po otevření velkých závorek a konstanta - jako výsledek integrace známého integrálu;-)

(3) Transformace provádíme v hranatých závorkách a do pravého integrálu dosadíme meze integrace.

(4) Vyjmeme „blikající světlo“ z hranatých závorek: a poté otevřete vnitřní závorky: .

(5) Zrušíme 1 a –1 v závorce a provedeme konečná zjednodušení.

Nakonec jsou nalezeny všechny tři Fourierovy koeficienty:

Dosadíme je do vzorce :

Zároveň nezapomeňte rozdělit na polovinu. V posledním kroku je konstanta („mínus dva“), která nezávisí na „en“, převzata mimo součet.

Tak jsme získali rozšíření funkce do Fourierovy řady na intervalu:

Podívejme se na problematiku konvergence Fourierovy řady. Vysvětlím zejména teorii Dirichletova věta, doslova "na prstech", takže pokud potřebujete striktní formulace, podívejte se prosím na učebnici na matematická analýza (například 2. díl Bohana; nebo 3. díl Fichtenholtze, ale je to složitější).

Druhá část úlohy vyžaduje nakreslení grafu, grafu součtu řady a grafu částečného součtu.

Graf funkce je obyčejná přímka v rovině, která je nakreslena černou tečkovanou čarou:

Pojďme zjistit součet série. Jak víte, funkční řady konvergují k funkcím. V našem případě zkonstruovaná Fourierova řada pro jakoukoli hodnotu "x" bude konvergovat k funkci, která je zobrazena červeně. Tato funkce trpí nespojitostmi 1. druhu v bodech, ale je v nich také definován (červené tečky na výkrese)

Tím pádem: . Je snadné vidět, že se znatelně liší od původní funkce, proto v záznamu Spíše než rovnítko se používá vlnovka.

Pojďme studovat algoritmus, který je vhodný pro konstrukci součtu řady.

Na centrálním intervalu Fourierova řada konverguje k samotné funkci (střední červený segment se shoduje s černou tečkovanou čarou lineární funkce).

Nyní si řekněme něco málo o povaze uvažovaného trigonometrického rozšíření. Fourierova řada jsou zahrnuty pouze periodické funkce (konstanta, sinus a kosinus), tedy součet řady je také periodická funkce.

Co to znamená v našem konkrétním příkladu? A to znamená, že součet řady – je jistě periodické a červený úsek intervalu se musí donekonečna opakovat vlevo i vpravo.

Myslím, že význam fráze „období rozkladu“ je nyní konečně jasný. Zjednodušeně řečeno, pokaždé se situace opakuje znovu a znovu.

V praxi obvykle stačí znázornit tři doby rozkladu, jak je to na výkrese. No a také „pahýly“ sousedních období - aby bylo jasné, že graf pokračuje.

Zvláště zajímavé jsou body diskontinuity 1. druhu. V takových bodech Fourierova řada konverguje k izolovaným hodnotám, které se nacházejí přesně uprostřed „skoku“ diskontinuity (červené tečky na výkrese). Jak zjistit pořadnici těchto bodů? Nejprve najdeme pořadnici „horního patra“: k tomu vypočítáme hodnotu funkce v pravém bodě centrální periody expanze: . Pro výpočet pořadnice „spodního patra“ je nejjednodušší použít extrém levá hodnota ze stejného období: . Ordináta průměrné hodnoty je aritmetickým průměrem součtu „nahoře a dole“: . Příjemným faktem je, že při konstrukci výkresu hned uvidíte, zda je střed vypočten správně nebo špatně.

Sestrojme částečný součet řady a zároveň zopakujme význam pojmu „konvergence“. Motiv je znám i z lekce o součtu číselné řady. Popišme naše bohatství podrobně:

Chcete-li sestavit částečný součet, musíte napsat nulu + další dva členy řady. to znamená,

Na výkresu je znázorněn graf funkce zelená, a jak je vidět, celou částku docela pevně „zabalí“. Pokud vezmeme v úvahu částečný součet pěti členů řady, pak graf této funkce ještě přesněji aproximuje červené čáry, pokud jich bude sto, pak „zelený had“ ve skutečnosti zcela splyne s červenými segmenty, atd. Fourierova řada tedy konverguje ke svému součtu.

Je zajímavé poznamenat, že jakýkoli částečný součet je spojitá funkce, ale celkový součet řady je stále nespojitý.

V praxi není tak vzácné sestrojit graf částečného součtu. Jak to udělat? V našem případě je nutné zvážit funkci na segmentu, vypočítat její hodnoty na koncích segmentu a v mezilehlých bodech (čím více bodů zvážíte, tím přesnější bude graf). Poté byste měli označit tyto body na výkresu a pečlivě nakreslit graf periody a poté jej „replikovat“ do sousedních intervalů. Jak jinak? Koneckonců, aproximace je také periodická funkce... ...v některých ohledech mi její graf připomíná plynulý srdeční rytmus na displeji lékařského zařízení.

Provádění konstrukce samozřejmě není příliš pohodlné, protože musíte být velmi opatrní a udržovat přesnost nejméně půl milimetru. Potěším však čtenáře, kterým kreslení nevyhovuje - v „opravdovém“ problému není vždy nutné provádět kreslení v cca 50 % případů je nutné funkci rozšířit do Fourierovy řady a je to .

Po dokončení výkresu dokončíme úkol:

Odpovědět :

V mnoha problémech funkce trpí diskontinuitou 1. druhu právě v období expanze:

Příklad 3

Rozšiřte funkci zadanou na intervalu do Fourierovy řady. Nakreslete graf funkce a celkového součtu řady.

Navržená funkce je specifikována po částech (a pozor, pouze na segmentu) a trpí diskontinuitou 1. druhu v bodě . Je možné vypočítat Fourierovy koeficienty? Žádný problém. Levá i pravá strana funkce jsou integrovatelné na svých intervalech, proto by integrály v každém ze tří vzorců měly být reprezentovány jako součet dvou integrálů. Podívejme se například, jak se to dělá pro nulový koeficient:

Druhý integrál se ukázal být roven nule, což snížilo práci, ale není tomu tak vždy.

Další dva Fourierovy koeficienty jsou popsány podobně.

Jak zobrazit součet řady? Na levém intervalu nakreslíme úsečku a na intervalu přímku (výsek osy zvýrazníme tučně a tučně). To znamená, že na intervalu rozšíření se součet řady shoduje s funkcí všude kromě tří „špatných“ bodů. V bodě diskontinuity funkce bude Fourierova řada konvergovat k izolované hodnotě, která se nachází přesně uprostřed „skoku“ diskontinuity. Není těžké to vidět orálně: levostranný limit: , pravostranný limit: a samozřejmě, ordináta středu je 0,5.

Vzhledem k periodicitě součtu je nutné obrázek „rozmnožit“ do sousedních období, zejména musí být totéž znázorněno na intervalech a . Současně bude v bodech Fourierova řada konvergovat k hodnotám mediánu.

Ve skutečnosti zde není nic nového.

Zkuste se s tímto úkolem vyrovnat sami. Přibližná ukázka finálního návrhu a nákres na konci lekce.

Expanze funkce do Fourierovy řady za libovolnou periodu

Pro libovolnou expanzní periodu, kde „el“ je jakékoli kladné číslo, se vzorce pro Fourierovy řady a Fourierovy koeficienty odlišují poněkud komplikovanějším argumentem pro sinus a kosinus:

Jestliže , pak dostaneme intervalové vzorce, se kterými jsme začali.

Algoritmus a principy řešení problému jsou zcela zachovány, ale zvyšuje se technická složitost výpočtů:

Příklad 4

Rozšiřte funkci na Fourierovu řadu a vykreslete součet.

Řešení: vlastně obdoba příkladu č. 3 s nespojitostí 1. druhu v bodě. V tomto problému je období expanze poloviční. Funkce je definována pouze na polovičním intervalu, ale to na věci nic nemění - důležité je, aby byly obě části funkce integrovatelné.

Rozšiřme funkci na Fourierovu řadu:

Protože funkce je na počátku nespojitá, každý Fourierův koeficient by měl být samozřejmě zapsán jako součet dvou integrálů:

1) První integrál napíšu co nejpodrobněji:

2) Pozorně se podíváme na povrch Měsíce:

Vezmeme druhý integrál po částech:

Na co si dát dobrý pozor poté, co pokračování řešení otevřeme hvězdičkou?

Za prvé, neztratíme první integrál , kde okamžitě aplikujeme diferenciální znaménko. Za druhé, nezapomeňte na nešťastnou konstantu před velkými závorkami a nenechte se zmást ve znacích při použití vzorce . Velké držáky je stále pohodlnější otevřít hned v dalším kroku.

Zbytek je otázkou techniky, potíže mohou být způsobeny pouze nedostatečnou zkušeností s řešením integrálů.

Ano, ne nadarmo byli významní kolegové francouzského matematika Fouriera rozhořčeni – jak si dovolil uspořádat funkce do goniometrických řad?! =) Mimochodem, každého asi zajímá praktický význam daného úkolu. Fourier sám pracoval na matematický model tepelné vodivosti a následně se po něm pojmenovaná řada začala využívat ke studiu mnoha periodických procesů, které jsou v okolním světě viditelné i neviditelné. Teď, mimochodem, jsem se přistihl, jak jsem si myslel, že to nebylo náhodou, že jsem porovnal graf druhého příkladu s periodickým rytmem srdce. Zájemci se mohou seznámit s praktickou aplikací Fourierova transformace ve zdrojích třetích stran. ...I když je lepší ne - bude se to pamatovat jako První láska =)

3) Vezmeme-li v úvahu opakovaně zmiňované slabé články, podívejme se na třetí koeficient:

Pojďme integrovat po částech:

Dosadíme do vzorce nalezené Fourierovy koeficienty , nezapomeňte rozdělit nulový koeficient na polovinu:

Nakreslete součet řady. Krátce postup zopakujeme: na intervalu sestrojíme přímku a na intervalu přímku. Pokud je hodnota „x“ nulová, vložíme bod doprostřed „skoku“ mezery a „replikujeme“ graf pro sousední období:

Na „spojení“ období se součet také bude rovnat středům „skoku“ mezery.

Připraveno. Dovolte mi připomenout, že samotná funkce je podmínkou definovaná pouze na polovičním intervalu a samozřejmě se shoduje se součtem řad na intervalech

Odpovědět :

Někdy je po částech daná funkce spojitá po dobu expanze. Nejjednodušší příklad: . Řešení (viz Bohan svazek 2) stejně jako ve dvou předchozích příkladech: i přes spojitost funkce v bodě je každý Fourierův koeficient vyjádřen jako součet dvou integrálů.

V intervalu rozšíření může být více bodů nespojitosti 1. druhu a/nebo „spojených“ bodů grafu (dva, tři a obecně libovolné finále Množství). Pokud je funkce integrovatelná na každé části, pak je také rozšiřitelná ve Fourierově řadě. Ale z praktické zkušenosti si tak krutou věc nepamatuji. Existují však obtížnější úkoly, než které byly právě uvažovány, a na konci článku jsou odkazy na Fourierovy řady se zvýšenou složitostí pro každého.

Mezitím se uvolníme, opřeme se v křeslech a rozjímáme o nekonečných rozlohách hvězd:

Příklad 5

Rozbalte funkci na Fourierovu řadu na intervalu a vykreslete součet řady.

V tomto problému je funkce spojitá na polovičním intervalu expanze, což zjednodušuje řešení. Vše je velmi podobné příkladu č. 2. Z vesmírné lodi není úniku - budete se muset rozhodnout =) Přibližná ukázka návrhu na konci lekce, rozvrh je přiložen.

Rozšíření Fourierových řad sudých a lichých funkcí

Pomocí sudých a lichých funkcí je proces řešení problému znatelně zjednodušen. A právě proto. Vraťme se k rozšíření funkce ve Fourierově řadě s periodou „dvě pí“ a libovolné období „dva el“ .

Předpokládejme, že naše funkce je sudá. Obecný termín řady, jak vidíte, obsahuje sudé kosiny a liché sinusy. A pokud rozšiřujeme funkci SUDÝ, tak proč potřebujeme liché sinus?! Vynulujeme zbytečný koeficient: .

Sudou funkci lze tedy rozšířit do Fourierovy řady pouze v kosinech:

Protože integrály sudých funkcí v integračním segmentu, který je symetrický vzhledem k nule, lze zdvojnásobit, jsou zbývající Fourierovy koeficienty také zjednodušeny.

Pro mezeru:

Pro libovolný interval:

Příklady učebnic, které lze nalézt téměř v každé učebnici matematické analýzy, zahrnují rozšíření sudých funkcí . Kromě toho jsem se s nimi několikrát setkal v mé osobní praxi:

Příklad 6

Funkce je dána. Požadované:

1) rozšiřte funkci na Fourierovu řadu s periodou , kde je libovolné kladné číslo;

2) zapište rozvoj na intervalu, sestrojte funkci a znázorněte celkový součet řady.

Řešení: V prvním odstavci je navrženo řešení problému v obecný pohled, a je to velmi pohodlné! V případě potřeby stačí nahradit svou hodnotu.

1) V tomto problému je období expanze poloviční. Během další akce, zejména během integrace je "el" považován za konstantu

Funkce je sudá, což znamená, že ji lze rozšířit do Fourierovy řady pouze v kosinech: .

Fourierovy koeficienty hledáme pomocí vzorců . Věnujte pozornost jejich bezpodmínečným výhodám. Za prvé, integrace se provádí přes pozitivní segment rozšíření, což znamená, že se modulu bezpečně zbavíme , vezmeme-li v úvahu pouze „X“ ze dvou kusů. A za druhé, integrace je znatelně zjednodušena.

Dva:

Pojďme integrovat po částech:

Tím pádem:
, zatímco konstanta , která nezávisí na „en“, je brána mimo součet.

Odpovědět :

2) Zapišme rozšíření na interval, pro tento účel v obecný vzorec nahradit požadovanou hodnotu půl cyklu:

Fourierovy řady jsou reprezentací libovolné funkce s určitou periodou ve formě řady. Obecně se toto řešení nazývá rozklad prvku podél ortogonální báze. Rozšíření funkcí do Fourierových řad je díky vlastnostem této transformace při integraci, derivaci a také posouvání výrazů argumentem a konvolucí poměrně silným nástrojem pro řešení různých problémů.

Člověk, který není obeznámen s vyšší matematikou, stejně jako s díly francouzského vědce Fouriera, s největší pravděpodobností nepochopí, co tyto „řady“ jsou a k čemu jsou potřeba. Mezitím se tato transformace zcela integrovala do našich životů. Používají ho nejen matematici, ale také fyzici, chemici, lékaři, astronomové, seismologové, oceánografové a mnoho dalších. Podívejme se také blíže na díla velkého francouzského vědce, který učinil objev, který předběhl dobu.

Člověk a Fourierova transformace

Fourierovy řady jsou jednou z metod (spolu s analýzou a dalšími k tomuto procesu dochází pokaždé, když člověk slyší zvuk). Naše ucho automaticky provádí transformaci elementární částice v elastickém médiu jsou v řadách (podél spektra) uspořádány po sobě jdoucí hodnoty úrovně hlasitosti pro tóny různých výšek. Dále mozek přemění tato data na zvuky, které jsou nám známé. To vše se děje bez naší touhy nebo vědomí, samo o sobě, ale abychom těmto procesům porozuměli, bude trvat několik let, než budeme studovat vyšší matematiku.

Více o Fourierově transformaci

Fourierova transformace může být provedena pomocí analytických, numerických a dalších metod. Fourierovy řady odkazují na numerickou metodu rozkladu jakýchkoli oscilačních procesů - od oceánských přílivů a světelných vln po cykly sluneční (a dalších astronomických objektů) aktivity. Pomocí těchto matematických technik můžete analyzovat funkce reprezentující jakékoli oscilační procesy jako řadu sinusových složek, které se pohybují od minima k maximu a zpět. Fourierova transformace je funkce, která popisuje fázi a amplitudu sinusoid odpovídající určité frekvenci. Tento proces lze využít k řešení velmi složitých rovnic, které popisují dynamické děje vznikající vlivem tepla, světla popř elektrická energie. Fourierovy řady také umožňují izolovat konstantní složky v komplexních oscilačních signálech, což umožňuje správně interpretovat experimentální pozorování získaná v medicíně, chemii a astronomii.

Historický odkaz

Zakladatelem této teorie je francouzský matematik Jean Baptiste Joseph Fourier. Tato transformace byla následně pojmenována po něm. Zpočátku vědec svou metodou studoval a vysvětloval mechanismy tepelné vodivosti – šíření tepla v pevné látky. Fourier navrhl, že počáteční nepravidelné rozložení lze rozložit na jednoduché sinusoidy, z nichž každá bude mít své vlastní teplotní minimum a maximum, stejně jako svou vlastní fázi. V tomto případě bude každá taková složka měřena od minima do maxima a naopak. Matematická funkce, která popisuje horní a dolní vrcholy křivky, stejně jako fázi každé z harmonických, se nazývá Fourierova transformace výrazu rozložení teploty. Autor teorie dal dohromady obecná funkce rozdělení, které je obtížné matematicky popsat, na velmi vhodnou řadu kosinus a sinus, které dohromady dávají původní rozdělení.

Princip transformace a názory současníků

Vědcovi současníci – přední matematici počátku devatenáctého století – tuto teorii nepřijali. Hlavní námitkou bylo Fourierovo tvrzení, že nespojitou funkci, popisující přímku nebo nespojitou křivku, lze reprezentovat jako součet sinusových výrazů, které jsou spojité. Jako příklad uvažujme krok Heaviside: jeho hodnota je nula vlevo od diskontinuity a jedna vpravo. Tato funkce popisuje závislost elektrického proudu na dočasné proměnné při sepnutí obvodu. Současníci tehdejší teorie se nikdy nesetkali s podobnou situací, kdy by nespojitý výraz byl popsán kombinací spojitých, běžných funkcí, jako je exponenciální, sinusová, lineární nebo kvadratická.

Co zmátlo francouzské matematiky na Fourierově teorii?

Koneckonců, pokud měl matematik ve svých tvrzeních pravdu, pak sečtením nekonečné goniometrické Fourierovy řady lze získat přesnou reprezentaci skokového výrazu, i když má mnoho podobných kroků. Na začátku devatenáctého století se takové tvrzení zdálo absurdní. Ale navzdory všem pochybnostem mnoho matematiků rozšířilo rozsah studia tohoto jevu a vzalo jej za rámec studia tepelné vodivosti. Většinu vědců však i nadále trápila otázka: „Může součet sinusové řady konvergovat k přesná hodnota diskontinuální funkce?

Konvergence Fourierovy řady: příklad

Otázka konvergence vyvstává vždy, když je potřeba sečíst nekonečné řady čísel. Chcete-li tomuto jevu porozumět, zvažte klasický příklad. Dokážete někdy dosáhnout na zeď, pokud bude každý následující krok poloviční než ten předchozí? Řekněme, že jste dva metry od cíle, první krok vás zavede na polovinu, další do tří čtvrtin a po pátém budete mít za sebou téměř 97 procent trasy. Bez ohledu na to, kolik kroků uděláte, nedosáhnete svého zamýšleného cíle v přísném matematickém smyslu. Pomocí numerických výpočtů lze dokázat, že je nakonec možné přiblížit se na danou vzdálenost. Tento důkaz je ekvivalentní k prokázání, že součet jedné poloviny, jedné čtvrtiny atd. bude mít tendenci k jednotě.

Otázka konvergence: Druhý příchod aneb Nástroj lorda Kelvina

Tato otázka byla znovu nastolena na konci devatenáctého století, kdy se pokusili použít Fourierovy řady k předpovědi intenzity přílivu a odlivu. V této době lord Kelvin vynalezl zařízení, které bylo analogové výpočetní zařízení, která umožnila vojenským a obchodním námořníkům sledovat tento přírodní jev. Tento mechanismus určoval sady fází a amplitud z tabulky výšek přílivu a odpovídajících časových bodů, pečlivě měřených v daném přístavu po celý rok. Každý parametr byl sinusovou složkou výrazu výšky přílivu a byl jednou z pravidelných složek. Měření byla vložena do výpočetního přístroje lorda Kelvina, který syntetizoval křivku, která předpovídala výšku vody jako funkci času pro následující rok. Velmi brzy byly podobné křivky nakresleny pro všechny přístavy světa.

Co když je proces narušen nespojitou funkcí?

V té době se zdálo zřejmé, že prediktor přílivové vlny s velkým počtem čítacích prvků dokáže vypočítat velký počet fází a amplitud a poskytnout tak přesnější předpovědi. Ukázalo se však, že tento vzorec není pozorován v případech, kdy slapový výraz, který by měl být syntetizován, obsahoval ostrý skok, to znamená, že byl nespojitý. Pokud jsou do zařízení zadána data z tabulky časových momentů, vypočítá několik Fourierových koeficientů. Původní funkce je obnovena díky sinusovým složkám (v souladu s nalezenými koeficienty). Nesoulad mezi původním a rekonstruovaným výrazem lze měřit v libovolném bodě. Při provádění opakovaných výpočtů a porovnávání je zřejmé, že hodnota největší chyby neklesá. Jsou však lokalizovány v oblasti odpovídající bodu diskontinuity a v jakémkoli jiném bodě mají tendenci k nule. V roce 1899 tento výsledek teoreticky potvrdil Joshua Willard Gibbs z Yale University.

Konvergence Fourierových řad a vývoj matematiky obecně

Fourierova analýza není použitelná pro výrazy obsahující nekonečný počet špiček v určitém intervalu. Obecně Fourierova řada, pokud je původní funkce reprezentována výsledkem reálné fyzický rozměr, vždy konvergovat. Otázky o konvergenci tohoto procesu pro konkrétní třídy funkcí vedly ke vzniku nových odvětví v matematice, například teorie zobecněných funkcí. Je spojována se jmény jako L. Schwartz, J. Mikusinski a J. Temple. V rámci této teorie jasné a přesné teoretický základ pod takovými výrazy, jako je Diracova delta funkce (popisuje oblast jedné oblasti soustředěné v nekonečně malém okolí bodu) a Heavisideův „krok“. Díky této práci se Fourierova řada stala použitelnou pro řešení rovnic a problémů zahrnujících intuitivní koncepty: bodový náboj, hmotnost bodu, magnetické dipóly a koncentrované zatížení svazku.

Fourierova metoda

Fourierovy řady v souladu s principy interference začínají rozkladem složitých forem na jednodušší. Například změna tepelného toku se vysvětluje jeho průchodem přes různé překážky z tepelně izolačního materiálu nepravidelného tvaru nebo změna povrchu země - zemětřesení, změna oběžné dráhy nebeské těleso- vliv planet. Zpravidla lze takové rovnice, které popisují jednoduché klasické systémy, snadno řešit pro každou jednotlivou vlnu. Fourier to ukázal jednoduchá řešení lze také shrnout, abychom získali řešení složitějších problémů. Z matematického hlediska jsou Fourierovy řady technikou pro reprezentaci výrazu jako součtu harmonických – kosinus a sinus. Proto tato analýza také známý jako harmonická analýza.

Fourierova řada - ideální technika před „věkem počítačů“

Před stvořením počítačové vybavení Fourierova technika byla nejlepší zbraní v arzenálu vědců při práci s vlnovou povahou našeho světa. Fourierova řada komplexní forma umožňuje rozhodnout nejen jednoduché úkoly, které jsou přístupné přímé aplikaci Newtonových zákonů mechaniky, ale také základních rovnic. Většinu objevů newtonovské vědy v devatenáctém století umožnila pouze Fourierova technika.

Fourierova řada dnes

S rozvojem počítačů se Fourierovy transformace zvedly na kvalitativně novou úroveň. Tato technika je pevně zavedena téměř ve všech oblastech vědy a techniky. Příkladem je digitální audio a video. Jeho implementace byla možná pouze díky teorii vyvinuté francouzským matematikem na začátku devatenáctého století. Fourierova řada tak v komplexní podobě umožnila průlom ve studiu kosmického prostoru. Kromě toho ovlivnila studium fyziky polovodičových materiálů a plazmatu, mikrovlnné akustiky, oceánografie, radaru a seismologie.

Trigonometrické Fourierovy řady

V matematice je Fourierova řada způsob reprezentace libovolného komplexní funkce součet jednodušších. V obecné případy počet takových výrazů může být nekonečný. Navíc, čím více je jejich počet při výpočtu zohledněn, tím přesnější je konečný výsledek. Nejčastěji se používá jako prvoci goniometrické funkce kosinus nebo sinus. V tomto případě se Fourierovy řady nazývají trigonometrické a řešení takových výrazů se nazývá harmonická expanze. Tato metoda hraje důležitá role v matematice. Především goniometrická řada poskytuje prostředek pro zobrazování a také studium funkcí, je hlavním aparátem teorie. Navíc umožňuje řešit řadu problémů z matematické fyziky. Nakonec tato teorie přispěla k rozvoji a uvedla v život řadu velmi důležitých úseků matematická věda(teorie integrálů, teorie periodických funkcí). Kromě toho posloužila jako výchozí bod pro vývoj následujících funkcí reálné proměnné a položila také základ pro harmonickou analýzu.

Fourierova řada periodických funkcí s periodou 2π.

Fourierova řada nám umožňuje studovat periodické funkce jejich rozkladem na složky. Typické jsou střídavé proudy a napětí, výchylky, rychlost a zrychlení klikových mechanismů a akustické vlny praktické příklady aplikace periodických funkcí v inženýrských výpočtech.

Rozšíření Fourierovy řady je založeno na předpokladu, že všechny funkce praktického významu v intervalu -π ≤x≤ π lze vyjádřit ve formě konvergentních goniometrických řad (řada je považována za konvergentní, jestliže posloupnost dílčích součtů složená z jejích členů konverguje):

Standardní (=obyčejný) zápis přes součet sinx a cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

kde a o, a 1,a 2,...,b 1,b 2,.. jsou reálné konstanty, tzn.

Kde pro rozsah od -π do π se koeficienty Fourierovy řady vypočítají pomocí vzorců:

Koeficienty a o , a n a b n se nazývají Fourierovy koeficienty, a pokud je lze nalézt, pak řada (1) se nazývá Fourierova řada odpovídající funkci f (x). Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nazývá první neboli základní harmonická,

Dalším způsobem, jak napsat řadu, je použít vztah acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Kde a o je konstanta, c 1 = (a 1 2 +b 1 2) 1/2, c n = (a n 2 +b n 2) 1/2 jsou amplitudy různých složek a rovná se a n =arctg a n /b n.

Pro řadu (1) se termín (a 1 cosx+b 1 sinx) nebo c 1 sin(x+α 1) nazývá první neboli základní harmonická, (a 2 cos2x+b 2 sin2x) nebo c 2 sin(2x +α 2) nazývaná druhá harmonická a tak dále.

Přesná reprezentace komplexního signálu obvykle vyžaduje nekonečný počet termínů. V mnoha praktických problémech však stačí vzít v úvahu pouze prvních několik termínů.

Fourierova řada neperiodických funkcí s periodou 2π.

Rozšíření neperiodických funkcí.

Pokud je funkce f(x) neperiodická, znamená to, že ji nelze rozšířit do Fourierovy řady pro všechny hodnoty x. Je však možné definovat Fourierovu řadu reprezentující funkci v libovolném rozsahu šířky 2π.

Vzhledem k neperiodické funkci lze novou funkci zkonstruovat výběrem hodnot f(x) v určitém rozsahu a jejich opakováním mimo tento rozsah v intervalech 2π. Protože je nová funkce periodická s periodou 2π, lze ji rozšířit do Fourierovy řady pro všechny hodnoty x. Například funkce f(x)=x není periodická. Pokud je však nutné ji rozšířit na Fourierovu řadu v intervalu od o do 2π, pak se mimo tento interval sestrojí periodická funkce s periodou 2π (jak je znázorněno na obrázku níže).

Pro neperiodické funkce, jako je f(x)=x, se součet Fourierovy řady rovná hodnotě f(x) ve všech bodech v daném rozsahu, ale u bodů se nerovná f(x). mimo rozsah. K nalezení Fourierovy řady neperiodické funkce v rozsahu 2π se používá stejný vzorec Fourierových koeficientů.

Sudé a liché funkce.

Říká se, že funkce y=f(x) je i když f(-x)=f(x) pro všechny hodnoty x. Grafy sudých funkcí jsou vždy symetrické podle osy y (tj. jsou to zrcadlové obrazy). Dva příklady sudých funkcí: y=x2 a y=cosx.

O funkci y=f(x) se říká, že je lichá, pokud f(-x)=-f(x) pro všechny hodnoty x. Grafy lichých funkcí jsou vždy symetrické podle počátku.

Mnoho funkcí není ani sudých, ani lichých.

Expanze Fourierovy řady v kosinech.

Fourierova řada sudé periodické funkce f(x) s periodou 2π obsahuje pouze kosinové členy (tj. žádné sinusové členy) a může zahrnovat konstantní člen. Proto,

kde jsou koeficienty Fourierovy řady,

Fourierova řada liché periodické funkce f(x) s periodou 2π obsahuje pouze členy se siny (tj. neobsahuje členy s kosiny).

Proto,

kde jsou koeficienty Fourierovy řady,

Fourierova řada v půlcyklu.

Pokud je funkce definována pro rozsah, řekněme od 0 do π, a nikoli pouze od 0 do 2π, lze ji v řadě rozšířit pouze v sinech nebo pouze v kosinech. Výsledná Fourierova řada se nazývá půlcyklová Fourierova řada.

Pokud chcete získat půlcyklový Fourierův rozvoj kosinů funkce f(x) v rozsahu od 0 do π, musíte sestrojit sudou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože dokonce funkce symetricky podle osy f(x) nakreslete čáru AB, jak je znázorněno na obr. níže. Pokud předpokládáme, že mimo uvažovaný interval získaná trojúhelníkový tvar je periodický s periodou 2π, pak výsledný graf vypadá, ukaž. na Obr. níže. Protože potřebujeme získat Fourierovu expanzi v kosinech, jako dříve, vypočítáme Fourierovy koeficienty a o a a n

Pokud chcete získat půlcyklový Fourierův rozvoj z hlediska sinů funkce f(x) v rozsahu od 0 do π, musíte sestrojit lichou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože lichá funkce je symetrická k počátku, sestrojíme úsečku CD, jak je znázorněno na obr. Předpokládáme-li, že mimo uvažovaný interval je výsledný pilový signál periodický s periodou 2π, pak má výsledný graf tvar znázorněný na Obr. Protože potřebujeme získat Fourierovu expanzi polocyklu v sinech, jako dříve, vypočítáme Fourierův koeficient. b

Fourierova řada pro libovolný interval.

Rozšíření periodické funkce s periodou L.

Periodická funkce f(x) se opakuje, když se x zvětšuje o L, tzn. f(x+L)=f(x). Přechod od dříve uvažovaných funkcí s periodou 2π k funkcím s periodou L je poměrně jednoduchý, protože jej lze provést pomocí změny proměnné.

Abychom našli Fourierovu řadu funkce f(x) v rozsahu -L/2≤x≤L/2, zavedeme novou proměnnou u, takže funkce f(x) má vůči u periodu 2π. Jestliže u=2πx/L, pak x=-L/2 pro u=-π a x=L/2 pro u=π. Nechť také f(x)=f(Lu/2π)=F(u). Fourierova řada F(u) má tvar

(Meze integrace lze nahradit libovolným intervalem délky L, například od 0 do L)

Fourierova řada na půlcyklu pro funkce zadané v intervalu L≠2π.

Pro substituci u=πх/L interval od x=0 do x=L odpovídá intervalu od u=0 do u=π. Funkce může být následně rozšířena do řady pouze v kosinech nebo pouze v sinech, tzn. do Fourierovy řady v polovičním cyklu.

Kosinusová expanze v rozsahu od 0 do L má tvar

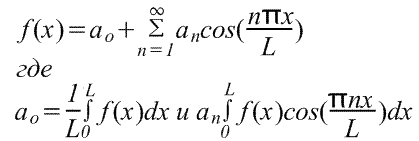
Funkce, jejich rozklad na komponenty. Střídavé proudy a napětí, výchylky, rychlost a zrychlení klikových mechanismů a akustické vlny jsou typickými praktickými příklady využití periodických funkcí v inženýrských výpočtech.

Standardní (=obyčejný) zápis přes součet sinx a cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

kde a o, a 1,a 2,...,b 1,b 2,.. jsou reálné konstanty, tzn.

Kde pro rozsah od -π do π se koeficienty Fourierovy řady vypočítají pomocí vzorců:

Dalším způsobem, jak napsat řadu, je použít vztah acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Kde a o je konstanta, c 1 = (a 1 2 +b 1 2) 1/2, c n = (a n 2 +b n 2) 1/2 jsou amplitudy různých složek a rovná se a n =arctg a n /b n.

Přesná reprezentace komplexního signálu obvykle vyžaduje nekonečný počet termínů. V mnoha praktických problémech však stačí vzít v úvahu pouze prvních několik termínů.

Fourierova řada neperiodických funkcí s periodou 2π. Rozšíření neperiodických funkcí do Fourierových řad.

Sudé a liché funkce.

O funkci y=f(x) se říká, že je lichá, pokud f(-x)=-f(x) pro všechny hodnoty x. Grafy lichých funkcí jsou vždy symetrické podle počátku.

Mnoho funkcí není ani sudých, ani lichých.

Expanze Fourierovy řady v kosinech.

Fourierova řada sudé periodické funkce f(x) s periodou 2π obsahuje pouze kosinové členy (tj. žádné sinusové členy) a může zahrnovat konstantní člen. Proto,

kde jsou koeficienty Fourierovy řady,

Fourierova řada liché periodické funkce f(x) s periodou 2π obsahuje pouze členy se siny (tj. neobsahuje členy s kosiny).

Proto,

kde jsou koeficienty Fourierovy řady,

Fourierova řada v půlcyklu.

Pokud chcete získat půlcyklový Fourierův rozvoj kosinů funkce f(x) v rozsahu od 0 do π, musíte sestrojit sudou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože sudá funkce je symetrická kolem osy f(x), nakreslíme přímku AB, jak je znázorněno na Obr. níže. Pokud předpokládáme, že mimo uvažovaný interval je výsledný trojúhelníkový tvar periodický s periodou 2π, pak výsledný graf vypadá takto: na Obr. níže. Protože potřebujeme získat Fourierovu expanzi v kosinech, jako dříve, vypočítáme Fourierovy koeficienty a o a a n

Pokud je potřeba získat funkce f(x) v rozsahu od 0 do π, pak je nutné sestrojit lichou periodickou funkci. Na Obr. Níže je funkce f(x)=x, postavená na intervalu od x=0 do x=π. Protože lichá funkce je symetrická k počátku, sestrojíme úsečku CD, jak je znázorněno na obr. Předpokládáme-li, že mimo uvažovaný interval je výsledný pilový signál periodický s periodou 2π, pak má výsledný graf tvar znázorněný na Obr. Protože potřebujeme získat Fourierovu expanzi polocyklu v sinech, jako dříve, vypočítáme Fourierův koeficient. b

Fourierova řada pro libovolný interval.

Rozšíření periodické funkce s periodou L.

Kde jsou koeficienty Fourierovy řady,

Častěji se však výše uvedený vzorec uvádí jako závislost na x. Protože u=2πx/L, znamená to du=(2π/L)dx a limity integrace jsou od -L/2 do L/2 místo - π do π. V důsledku toho má Fourierova řada pro závislost na x tvar

kde v rozsahu od -L/2 do L/2 jsou koeficienty Fourierovy řady,

(Meze integrace lze nahradit libovolným intervalem délky L, například od 0 do L)

Fourierova řada na půlcyklu pro funkce zadané v intervalu L≠2π.

Kosinusová expanze v rozsahu od 0 do L má tvar

Jak vložit matematické vzorce na web?

Pokud někdy budete potřebovat přidat jeden nebo dva matematické vzorce na webovou stránku, pak nejjednodušší způsob, jak to udělat, je ten, který je popsán v článku: matematické vzorce lze snadno vložit na web ve formě obrázků, které automaticky generuje Wolfram Alpha . Tato univerzální metoda kromě jednoduchosti pomůže zlepšit viditelnost webu vyhledávače. Funguje to už dlouho (a myslím, že bude fungovat navždy), ale už je morálně zastaralé.

Pokud na svém webu pravidelně používáte matematické vzorce, pak vám doporučuji používat MathJax – speciální knihovnu JavaScript, která zobrazuje matematický zápis ve webových prohlížečích pomocí značek MathML, LaTeX nebo ASCIIMathML.

Existují dva způsoby, jak začít používat MathJax: (1) pomocí jednoduchého kódu můžete ke své webové stránce rychle připojit skript MathJax, který se ve správný čas automaticky načte ze vzdáleného serveru (seznam serverů); (2) stáhněte si skript MathJax ze vzdáleného serveru na váš server a připojte jej ke všem stránkám vašeho webu. Druhý způsob – složitější a časově náročnější – urychlí načítání stránek vašeho webu, a pokud se nadřazený server MathJax z nějakého důvodu stane dočasně nedostupným, váš vlastní web to nijak neovlivní. I přes tyto výhody jsem zvolil první metodu, protože je jednodušší, rychlejší a nevyžaduje technické dovednosti. Postupujte podle mého příkladu a za pouhých 5 minut budete moci na svém webu používat všechny funkce MathJax.

Skript knihovny MathJax můžete připojit ze vzdáleného serveru pomocí dvou možností kódu převzatých z hlavního webu MathJax nebo na stránce dokumentace:

Jednu z těchto možností kódu je třeba zkopírovat a vložit do kódu vaší webové stránky, nejlépe mezi značky a nebo bezprostředně za značku. Podle první možnosti se MathJax načítá rychleji a méně zpomaluje stránku. Ale druhá možnost automaticky sleduje a načítá nejnovější verze MathJax. Pokud vložíte první kód, bude nutné jej pravidelně aktualizovat. Pokud vložíte druhý kód, stránky se budou načítat pomaleji, ale nebudete muset neustále sledovat aktualizace MathJax.

Nejjednodušší způsob, jak připojit MathJax, je v Bloggeru nebo WordPressu: do ovládacího panelu webu přidejte widget určený pro vložení kódu JavaScript třetí strany, zkopírujte do něj první nebo druhou verzi výše uvedeného kódu pro stahování a umístěte widget blíže. na začátek šablony (mimochodem to není vůbec nutné, protože skript MathJax se načítá asynchronně). To je vše. Nyní se naučte syntaxi značek MathML, LaTeX a ASCIIMathML a jste připraveni vkládat matematické vzorce do webových stránek svého webu.

Jakýkoli fraktál je konstruován podle určitého pravidla, které je důsledně aplikováno neomezeně mnohokrát. Každý takový čas se nazývá iterace.

Iterační algoritmus pro konstrukci Mengerovy houby je poměrně jednoduchý: původní krychle se stranou 1 je rozdělena rovinami rovnoběžnými s jejími plochami na 27 stejných krychlí. Odebere se z ní jedna centrální krychle a 6 k ní přiléhajících krychlí podél stěn. Výsledkem je sada skládající se ze zbývajících 20 menších kostek. Když uděláme totéž s každou z těchto kostek, získáme sadu skládající se ze 400 menších kostek. Pokračujeme-li v tomto procesu donekonečna, získáme Mengerovu houbu.