ढूँढ़ने के लिए एक त्रिकोणमितीय फ़ंक्शन का व्युत्पन्न उपयोग करने की आवश्यकता डेरिवेटिव की तालिका, अर्थात् डेरिवेटिव 6-13।
जब तुम पाओगे प्राइम डेरिवेटिव त्रिकोणमितीय कार्य सामान्य गलतियों से बचने के लिए आपको निम्नलिखित बातों पर ध्यान देना चाहिए:
- फ़ंक्शन अभिव्यक्ति में, शब्दों में से एक अक्सर होता है साइन, कोसाइन या अन्य त्रिकोणमितीय फ़ंक्शनफ़ंक्शन के तर्क से नहीं, बल्कि संख्या (स्थिर) से, इसलिए इस पद का व्युत्पन्न शून्य के बराबर है;
- लगभग हमेशा आपको विभेदन के परिणामस्वरूप प्राप्त अभिव्यक्ति को सरल बनाने की आवश्यकता होती है, और इसके लिए आपको भिन्नों के साथ संचालन के ज्ञान का आत्मविश्वास से उपयोग करने की आवश्यकता होती है;
- किसी अभिव्यक्ति को सरल बनाने के लिए, आपको लगभग हमेशा त्रिकोणमितीय सर्वसमिकाओं को जानने की आवश्यकता होती है, उदाहरण के लिए, सूत्र दोहरा कोणऔर ज्या और कोज्या के वर्गों के योग के रूप में एकता का सूत्र।
उदाहरण 1।किसी फ़ंक्शन का व्युत्पन्न खोजें
समाधान। चलो साथ कहते हैं कोसाइन का व्युत्पन्नसब कुछ स्पष्ट है, जो लोग डेरिवेटिव का अध्ययन करना शुरू करते हैं वे कहेंगे। किस बारे में साइन का व्युत्पन्नबारह को पाई से विभाजित किया गया? उत्तर: इसे शून्य के बराबर मानें! यहां साइन (आखिरकार एक फ़ंक्शन!) एक जाल है, क्योंकि तर्क वेरिएबल एक्स या कोई अन्य वेरिएबल नहीं है, बल्कि सिर्फ एक संख्या है। अर्थात् इस संख्या की ज्या भी एक संख्या है। और किसी संख्या (स्थिरांक) का व्युत्पन्न, जैसा कि हम व्युत्पन्न तालिका से जानते हैं, शून्य के बराबर है। इसलिए, हम केवल X की ऋण ज्या को छोड़ते हैं और इसके व्युत्पन्न का पता लगाते हैं, चिह्न के बारे में नहीं भूलते:
![]() .
.
उदाहरण 2.किसी फ़ंक्शन का व्युत्पन्न खोजें
![]() .
.
समाधान। दूसरा पद पिछले उदाहरण के पहले पद के समान ही है। अर्थात्, यह एक संख्या है, और संख्या का व्युत्पन्न शून्य है। हम दूसरे पद के व्युत्पन्न को भागफल के व्युत्पन्न के रूप में पाते हैं:
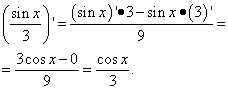
उदाहरण 3.किसी फ़ंक्शन का व्युत्पन्न खोजें
समाधान। यह एक और समस्या है: यहां पहले पद में कोई आर्कसाइन या अन्य त्रिकोणमितीय फलन नहीं है, लेकिन x है, जिसका अर्थ है कि यह x का एक फलन है। इसलिए, हम इसे कार्यों के योग में एक पद के रूप में अलग करते हैं:

यहां भिन्नों के साथ संचालन में कौशल की आवश्यकता थी, अर्थात् भिन्न की तीन-मंजिला संरचना को खत्म करने में।
उदाहरण 4.किसी फ़ंक्शन का व्युत्पन्न खोजें
![]() .
.
समाधान। यहां अक्षर "फी" पिछले मामलों में (और अधिकांश अन्य में, लेकिन सभी में नहीं) "एक्स" के समान भूमिका निभाता है - स्वतंत्र चर। इसलिए, जब हम कार्यों के उत्पाद के व्युत्पन्न की तलाश करते हैं, तो हम "फी" की जड़ के व्युत्पन्न को शून्य के बराबर घोषित करने में जल्दबाजी नहीं करेंगे। इसलिए:
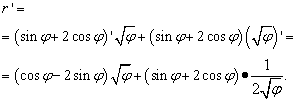
लेकिन समाधान यहीं ख़त्म नहीं होता. चूँकि समान पद दो कोष्ठकों में एकत्रित हैं, इसलिए हमें अभी भी अभिव्यक्ति को रूपांतरित (सरलीकृत) करने की आवश्यकता है। इसलिए, हम कोष्ठकों को उनके पीछे के कारकों से गुणा करते हैं, और फिर हम पदों को एक सामान्य हर में लाते हैं और अन्य प्राथमिक परिवर्तन करते हैं:

उदाहरण 5.किसी फ़ंक्शन का व्युत्पन्न खोजें
समाधान। इस उदाहरण में, हमें इस तथ्य को जानने की आवश्यकता होगी कि कोसाइन के माध्यम से एक ऐसा त्रिकोणमितीय फ़ंक्शन - सेकेंट - और इसके सूत्र मौजूद हैं। आइए अंतर करें:

उदाहरण 6.किसी फ़ंक्शन का व्युत्पन्न खोजें
![]() .
.
समाधान। इस उदाहरण में, हमें स्कूल का दोहरा कोण फॉर्मूला याद रखना होगा। लेकिन पहले आइए अंतर करें:

![]() ,
,
(यह द्विकोण सूत्र है)
व्युत्क्रम त्रिकोणमितीय फलनों के व्युत्पन्न और उनके सूत्रों की व्युत्पत्ति प्रस्तुत की गई है। उच्च क्रम के डेरिवेटिव के लिए अभिव्यक्तियाँ भी दी गई हैं। सूत्रों की व्युत्पत्ति के अधिक विस्तृत विवरण वाले पृष्ठों के लिंक।
सबसे पहले, हम आर्क्साइन के व्युत्पन्न के लिए सूत्र प्राप्त करते हैं। होने देना
य = आर्कसिन एक्स.
चूँकि आर्क्साइन, साइन का व्युत्क्रम फलन है
.
यहाँ y, x का एक फलन है। चर x के संबंध में अंतर करें:
.
हम आवेदन करते हैं:
.
तो हमने पाया:
.
क्योंकि तब । तब
.
और पिछला सूत्र इस प्रकार बनता है:
. यहाँ से
.
ठीक इसी प्रकार, आप चाप कोज्या के अवकलज का सूत्र प्राप्त कर सकते हैं। हालाँकि, व्युत्क्रम त्रिकोणमितीय फलनों से संबंधित सूत्र का उपयोग करना आसान है:
.
तब
.
अधिक विस्तृत विवरण "आर्क्साइन और आर्ककोसाइन के व्युत्पन्नों की व्युत्पत्ति" पृष्ठ पर प्रस्तुत किया गया है। वहां यह दिया गया है दो प्रकार से व्युत्पन्न की व्युत्पत्ति- ऊपर चर्चा की गई है और व्युत्क्रम फलन के अवकलज के सूत्र के अनुसार।
आर्कटैन्जेंट और आर्ककोटैंजेंट के व्युत्पन्नों की व्युत्पत्ति
इसी प्रकार हम आर्कटेन्जेंट और आर्ककोटैंजेंट के व्युत्पन्न ढूंढेंगे।
होने देना
य = आर्कटान एक्स.
आर्कटेंजेंट स्पर्शरेखा का व्युत्क्रम कार्य है:
.
चर x के संबंध में अंतर करें:
.
हम एक जटिल फ़ंक्शन के व्युत्पन्न के लिए सूत्र लागू करते हैं:
.
तो हमने पाया:
.
चाप कोटैंजेंट का व्युत्पन्न:
.
आर्क्साइन डेरिवेटिव
होने देना
.
हमने आर्क्साइन का प्रथम-क्रम व्युत्पन्न पहले ही पा लिया है:
.
विभेदन करके, हम दूसरे क्रम का व्युत्पन्न पाते हैं:
;
.
इसे निम्नलिखित रूप में भी लिखा जा सकता है:
.
यहीं से हमें मिलता है अंतर समीकरण, जो पहले और दूसरे क्रम के आर्क्साइन डेरिवेटिव से संतुष्ट है:
.
इस समीकरण को विभेदित करके, हम उच्च कोटि के व्युत्पन्न ज्ञात कर सकते हैं।
nवें क्रम के आर्क्साइन का व्युत्पन्न
nवें क्रम के आर्क्साइन के व्युत्पन्न का निम्नलिखित रूप है:
,
घात का बहुपद कहाँ है? यह सूत्रों द्वारा निर्धारित किया जाता है:
;
.
यहाँ ।
बहुपद अवकल समीकरण को संतुष्ट करता है:
.
nवें क्रम के आर्ककोसाइन का व्युत्पन्न
त्रिकोणमितीय सूत्र का उपयोग करके आर्क कोसाइन के डेरिवेटिव आर्क साइन के डेरिवेटिव से प्राप्त किए जाते हैं:
.
इसलिए, इन कार्यों के व्युत्पन्न केवल संकेत में भिन्न होते हैं:
.
आर्कटेंजेंट के व्युत्पन्न
होने देना । हमने पहले क्रम के चाप कोटैंजेंट का व्युत्पन्न पाया:
.
आइए भिन्न को उसके सरलतम रूप में तोड़ें:
.
यहाँ काल्पनिक इकाई है, .
हम एक बार अंतर करते हैं और भिन्न को एक सामान्य हर में लाते हैं:
.
प्रतिस्थापित करने पर, हमें प्राप्त होता है:
.
nवें क्रम के चापस्पर्शज्या का व्युत्पन्न
इस प्रकार, nवें क्रम के चाप स्पर्शरेखा के व्युत्पन्न को कई तरीकों से दर्शाया जा सकता है:
;
.
चाप कोटैंजेंट के व्युत्पन्न
अब रहने दो. आइए व्युत्क्रम त्रिकोणमितीय फलनों को जोड़ने वाला सूत्र लागू करें:
.
तब चाप स्पर्शरेखा का nवाँ क्रम व्युत्पन्न चाप स्पर्शरेखा के व्युत्पन्न से केवल चिह्न में भिन्न होता है:
.
प्रतिस्थापित करने पर, हम पाते हैं:
.
सन्दर्भ:
एन.एम. गुंटर, आर.ओ. कुज़मिन, उच्च गणित में समस्याओं का संग्रह, "लैन", 2003।
तालिका का पहला सूत्र निकालते समय, हम एक बिंदु पर व्युत्पन्न फ़ंक्शन की परिभाषा से आगे बढ़ेंगे। चलो कहाँ ले चलो एक्स- कोई भी वास्तविक संख्या, अर्थात, एक्स- फ़ंक्शन की परिभाषा के क्षेत्र से कोई भी संख्या। आइए फ़ंक्शन की वृद्धि और तर्क की वृद्धि के अनुपात की सीमा को यहां लिखें: ![]()
यह ध्यान दिया जाना चाहिए कि सीमा चिह्न के तहत अभिव्यक्ति प्राप्त की जाती है, जो शून्य से विभाजित शून्य की अनिश्चितता नहीं है, क्योंकि अंश में एक अनंत मान नहीं होता है, लेकिन सटीक शून्य होता है। दूसरे शब्दों में, एक स्थिर फलन की वृद्धि सदैव शून्य होती है।
इस प्रकार, एक स्थिर फलन का व्युत्पन्नपरिभाषा के संपूर्ण क्षेत्र में शून्य के बराबर है.
एक शक्ति फलन का व्युत्पन्न.
व्युत्पन्न सूत्र ऊर्जा समीकरणकी तरह लगता है ![]() , जहां प्रतिपादक पी- कोई भी वास्तविक संख्या।
, जहां प्रतिपादक पी- कोई भी वास्तविक संख्या।
आइए सबसे पहले प्राकृतिक घातांक, अर्थात्, के लिए सूत्र सिद्ध करें पी = 1, 2, 3, ...
हम व्युत्पन्न की परिभाषा का उपयोग करेंगे। आइए हम किसी पावर फ़ंक्शन की वृद्धि और तर्क की वृद्धि के अनुपात की सीमा लिखें: 
अंश में व्यंजक को सरल बनाने के लिए, हम न्यूटन द्विपद सूत्र की ओर मुड़ते हैं: 
इस तरह, 
यह एक प्राकृतिक घातांक के लिए घात फलन के व्युत्पन्न के सूत्र को सिद्ध करता है।
एक घातीय फलन का व्युत्पन्न.
हम परिभाषा के आधार पर व्युत्पन्न सूत्र की व्युत्पत्ति प्रस्तुत करते हैं:
हम अनिश्चितता पर आ गये हैं। इसका विस्तार करने के लिए, हम एक नया वेरिएबल पेश करते हैं, और पर। तब । पिछले संक्रमण में, हमने एक नए लघुगणकीय आधार पर संक्रमण के लिए सूत्र का उपयोग किया था।
आइए मूल सीमा में स्थानापन्न करें: 
यदि हम दूसरी उल्लेखनीय सीमा को याद करते हैं, तो हम घातीय फ़ंक्शन के व्युत्पन्न के सूत्र पर पहुंचते हैं: 
लघुगणकीय फलन का व्युत्पन्न.
आइए हम सभी के लिए एक लघुगणकीय फलन के अवकलज का सूत्र सिद्ध करें एक्सपरिभाषा के क्षेत्र और आधार के सभी मान्य मानों से एलोगारित्म व्युत्पन्न की परिभाषा के अनुसार हमारे पास है: 
जैसा कि आपने देखा, प्रमाण के दौरान परिवर्तन लघुगणक के गुणों का उपयोग करके किए गए थे। समानता  दूसरी उल्लेखनीय सीमा के कारण सत्य है।
दूसरी उल्लेखनीय सीमा के कारण सत्य है।
त्रिकोणमितीय कार्यों के व्युत्पन्न।
त्रिकोणमितीय फलनों के व्युत्पन्नों के लिए सूत्र प्राप्त करने के लिए, हमें कुछ त्रिकोणमिति सूत्रों के साथ-साथ पहली उल्लेखनीय सीमा को भी याद करना होगा।
हमारे पास साइन फ़ंक्शन के लिए व्युत्पन्न की परिभाषा है ![]() .
.
आइए ज्या के अंतर सूत्र का उपयोग करें: 
पहली उल्लेखनीय सीमा की ओर मुड़ना बाकी है: 
इस प्रकार, फ़ंक्शन का व्युत्पन्न पाप एक्सवहाँ है क्योंकि x.
कोज्या के अवकलज का सूत्र बिल्कुल इसी प्रकार सिद्ध किया जाता है। 
इसलिए, फ़ंक्शन का व्युत्पन्न क्योंकि xवहाँ है -पाप एक्स.
हम विभेदन (अंश का व्युत्पन्न) के सिद्ध नियमों का उपयोग करके स्पर्शरेखा और कोटैंजेंट के व्युत्पन्न की तालिका के लिए सूत्र प्राप्त करेंगे। 
अतिशयोक्तिपूर्ण कार्यों के व्युत्पन्न.
विभेदीकरण के नियम और डेरिवेटिव की तालिका से घातीय फ़ंक्शन के व्युत्पन्न के लिए सूत्र हमें हाइपरबोलिक साइन, कोसाइन, टेंगेंट और कोटैंजेंट के डेरिवेटिव के लिए सूत्र प्राप्त करने की अनुमति देते हैं। 
व्युत्क्रम फलन का व्युत्पन्न.
प्रेजेंटेशन के दौरान भ्रम से बचने के लिए, आइए सबस्क्रिप्ट में उस फ़ंक्शन के तर्क को निरूपित करें जिसके द्वारा विभेदीकरण किया जाता है, अर्थात यह फ़ंक्शन का व्युत्पन्न है एफ(एक्स)द्वारा एक्स.
अब आइये सूत्रीकरण करें व्युत्क्रम फलन का अवकलज ज्ञात करने का नियम।
चलो कार्य करें वाई = एफ(एक्स)और एक्स = जी(वाई)परस्पर व्युत्क्रम, अंतरालों पर परिभाषित और क्रमशः। यदि किसी बिंदु पर फ़ंक्शन का एक सीमित गैर-शून्य व्युत्पन्न है एफ(एक्स), तो बिंदु पर व्युत्क्रम फलन का एक परिमित व्युत्पन्न होता है जी(वाई), और ![]() . एक अन्य पोस्ट में
. एक अन्य पोस्ट में ![]() .
.
इस नियम को किसी के लिए भी दोबारा बनाया जा सकता है एक्सअंतराल से, तब हम पाते हैं  .
.
आइए इन फॉर्मूलों की वैधता की जाँच करें।
आइए प्राकृतिक लघुगणक के लिए व्युत्क्रम फलन खोजें ![]() (यहाँ यएक फ़ंक्शन है, और एक्स- तर्क)। इस समीकरण को हल करने के बाद एक्स, हमें (यहाँ) मिलता है एक्सएक फ़ंक्शन है, और य- उसका तर्क)। वह है,
(यहाँ यएक फ़ंक्शन है, और एक्स- तर्क)। इस समीकरण को हल करने के बाद एक्स, हमें (यहाँ) मिलता है एक्सएक फ़ंक्शन है, और य- उसका तर्क)। वह है, ![]() और परस्पर विपरीत कार्य।
और परस्पर विपरीत कार्य।
डेरिवेटिव की तालिका से हम इसे देखते हैं ![]() और
और ![]() .
.
आइए सुनिश्चित करें कि व्युत्क्रम फ़ंक्शन के व्युत्पन्न खोजने के सूत्र हमें समान परिणामों तक ले जाते हैं: 
ज्यामिति और गणित के पाठ्यक्रम से, स्कूली बच्चे इस तथ्य के आदी हो गए हैं कि व्युत्पन्न की अवधारणा उन्हें एक आकृति के क्षेत्र, अंतर, कार्यों की सीमाओं के साथ-साथ सीमाओं के माध्यम से बताई जाती है। आइए व्युत्पन्न की अवधारणा को एक अलग कोण से देखने का प्रयास करें, और निर्धारित करें कि व्युत्पन्न और त्रिकोणमितीय कार्यों को कैसे जोड़ा जा सकता है।
तो, आइए कुछ मनमाने वक्र पर विचार करें जो अमूर्त फ़ंक्शन y = f(x) द्वारा वर्णित है।
आइए कल्पना करें कि अनुसूची एक पर्यटक मार्ग का मानचित्र है। चित्र में वृद्धि ∆x (डेल्टा x) पथ की एक निश्चित दूरी है, और ∆y समुद्र तल से पथ की ऊंचाई में परिवर्तन है।
फिर यह पता चलता है कि अनुपात ∆x/∆y मार्ग के प्रत्येक खंड पर मार्ग की जटिलता को चित्रित करेगा। इस मूल्य को जानने के बाद, आप आत्मविश्वास से कह सकते हैं कि क्या चढ़ाई/उतरन तीव्र है, क्या आपको चढ़ाई के उपकरण की आवश्यकता होगी और क्या पर्यटकों को एक निश्चित की आवश्यकता होगी शारीरिक प्रशिक्षण. लेकिन यह सूचक केवल एक छोटे अंतराल ∆x के लिए मान्य होगा।
यदि यात्रा का आयोजक पथ के आरंभ और समाप्ति बिंदुओं के लिए मान लेता है, अर्थात, ∆x मार्ग की लंबाई के बराबर है, तो वह कठिनाई की डिग्री पर वस्तुनिष्ठ डेटा प्राप्त नहीं कर पाएगा यात्रा का. इसलिए, एक और ग्राफ़ बनाना आवश्यक है जो पथ में परिवर्तनों की गति और "गुणवत्ता" को चित्रित करेगा, दूसरे शब्दों में, मार्ग के प्रत्येक "मीटर" के लिए अनुपात ∆x/∆y निर्धारित करेगा।
यह ग्राफ़ एक विशिष्ट पथ के लिए एक दृश्य व्युत्पन्न होगा और रुचि के प्रत्येक अंतराल पर इसके परिवर्तनों का निष्पक्ष रूप से वर्णन करेगा। इसे सत्यापित करना बहुत सरल है; मान ∆x/∆y x और y के विशिष्ट मान के लिए लिए गए अंतर से अधिक कुछ नहीं है। आइए हम विभेदन को विशिष्ट निर्देशांकों पर नहीं, बल्कि समग्र रूप से फ़ंक्शन पर लागू करें:

व्युत्पन्न और त्रिकोणमितीय कार्य
त्रिकोणमितीय फलन व्युत्पन्नों के साथ अटूट रूप से जुड़े हुए हैं। इसे निम्नलिखित चित्र से समझा जा सकता है। निर्देशांक अक्ष का चित्र फ़ंक्शन Y = f (x) - नीला वक्र दिखाता है।
K (x0; f (x0)) एक मनमाना बिंदु है, x0 + ∆x OX अक्ष के साथ वृद्धि है, और f (x0 + ∆x) एक निश्चित बिंदु L पर OY अक्ष के साथ वृद्धि है।

आइए बिंदु K और L से होकर एक सीधी रेखा खींचें और निर्माण करें सही त्रिकोणकेएलएन. यदि आप मानसिक रूप से खंड LN को ग्राफ़ Y = f (x) के साथ ले जाते हैं, तो बिंदु L और N मान K (x0; f (x0)) की ओर प्रवृत्त होंगे। आइए इस बिंदु को ग्राफ़ की सशर्त शुरुआत कहें - सीमा; यदि फ़ंक्शन अनंत है, कम से कम एक अंतराल पर, यह प्रवृत्ति भी अनंत होगी, और इसका सीमित मान 0 के करीब है।
इस प्रवृत्ति की प्रकृति को चयनित बिंदु y = kx + b के स्पर्शरेखा द्वारा या मूल फ़ंक्शन डाई - हरी सीधी रेखा के व्युत्पन्न के ग्राफ़ द्वारा वर्णित किया जा सकता है।
लेकिन यहाँ त्रिकोणमिति कहाँ है?! सब कुछ बहुत सरल है, समकोण त्रिभुज KLN पर विचार करें। किसी विशिष्ट बिंदु K के लिए अंतर मान कोण α या ∠K की स्पर्शरेखा है:

इस प्रकार, हम व्युत्पन्न के ज्यामितीय अर्थ और त्रिकोणमितीय कार्यों के साथ उसके संबंध का वर्णन कर सकते हैं।
त्रिकोणमितीय कार्यों के लिए व्युत्पन्न सूत्र
व्युत्पन्न का निर्धारण करते समय साइन, कोसाइन, स्पर्शरेखा और कोटैंजेंट के परिवर्तनों को याद रखना चाहिए।

अंतिम दो सूत्र कोई त्रुटि नहीं हैं, मुद्दा यह है कि एक साधारण तर्क के व्युत्पन्न और एक ही क्षमता में एक फ़ंक्शन को परिभाषित करने के बीच अंतर है।
आइए साइनस, कोसाइन, स्पर्शज्या और कोटैंजेंट के व्युत्पन्नों के सूत्रों के साथ एक तुलनात्मक तालिका देखें:

आर्क्साइन, आर्ककोसाइन, आर्कटैंजेंट और आर्ककोटैंजेंट के व्युत्पन्नों के लिए भी सूत्र निकाले गए हैं, हालांकि इनका उपयोग बहुत ही कम किया जाता है:

यह ध्यान देने योग्य है कि उपरोक्त सूत्र विशिष्ट यूएसई कार्यों को सफलतापूर्वक हल करने के लिए स्पष्ट रूप से पर्याप्त नहीं हैं, जो त्रिकोणमितीय अभिव्यक्ति के व्युत्पन्न को खोजने के एक विशिष्ट उदाहरण को हल करते समय प्रदर्शित किया जाएगा।
व्यायाम: फ़ंक्शन का व्युत्पन्न ज्ञात करना और π/4 के लिए इसका मान ज्ञात करना आवश्यक है:

समाधान: 'y' को खोजने के लिए मूल फ़ंक्शन को व्युत्पन्न में परिवर्तित करने के लिए मूल सूत्रों को याद करना आवश्यक है।
विषय:"त्रिकोणमितीय कार्यों का व्युत्पन्न"।
पाठ का प्रकार- ज्ञान को समेकित करने का एक पाठ।
पाठ रूप- एकीकृत पाठ.
इस अनुभाग के लिए पाठ प्रणाली में पाठ का स्थान- सामान्य पाठ.
लक्ष्य व्यापक रूप से निर्धारित किए गए हैं:
- शैक्षिक:विभेदीकरण के नियमों को जानें, समीकरणों और असमानताओं को हल करते समय डेरिवेटिव की गणना के नियमों को लागू करने में सक्षम हों; कम्प्यूटेशनल, कौशल और क्षमताओं सहित विषय में सुधार; कंप्यूटर कौशल;
- विकसित होना:बौद्धिक और तार्किक कौशल और संज्ञानात्मक रुचियों का विकास;
- शैक्षिक:के प्रति अनुकूलनशीलता विकसित करें आधुनिक स्थितियाँप्रशिक्षण।
तरीके:
- प्रजनन और उत्पादक;
- व्यावहारिक और मौखिक;
- स्वतंत्र काम;
- क्रमादेशित शिक्षण, टी.एस.ओ.;
- ललाट, समूह और का संयोजन व्यक्तिगत काम;
- विभेदित शिक्षा;
- प्रेरक निगमन।
नियंत्रण के रूप:
- मौखिक सर्वेक्षण,
- क्रमादेशित नियंत्रण,
- स्वतंत्र काम,
- कंप्यूटर पर व्यक्तिगत कार्य,
- छात्र के डायग्नोस्टिक कार्ड का उपयोग करके सहकर्मी समीक्षा।
कक्षाओं के दौरान
I. संगठनात्मक क्षण
द्वितीय. संदर्भ ज्ञान का अद्यतनीकरण
क) लक्ष्यों और उद्देश्यों का संचार करना:
- विभेदीकरण के नियमों को जानें, समस्याओं, समीकरणों और असमानताओं को हल करते समय डेरिवेटिव की गणना के नियमों को लागू करने में सक्षम हों;
- कम्प्यूटेशनल, कौशल और क्षमताओं सहित विषय में सुधार; कंप्यूटर कौशल;
- बौद्धिक और तार्किक कौशल और संज्ञानात्मक रुचियों का विकास करना;
- आधुनिक शिक्षण परिस्थितियों के प्रति अनुकूलन क्षमता विकसित करना।
बी) शैक्षिक सामग्री की पुनरावृत्ति
डेरिवेटिव की गणना के नियम (ध्वनि के साथ कंप्यूटर पर सूत्रों की पुनरावृत्ति)। दस्तावेज़.7.
- साइन का व्युत्पन्न क्या है?
- कोसाइन का व्युत्पन्न क्या है?
- स्पर्शरेखा का व्युत्पन्न क्या है?
- कोटैंजेंट का व्युत्पन्न क्या है?
तृतीय. मौखिक कार्य
व्युत्पन्न खोजें. |
|||
विकल्प 1। |
विकल्प 2। |
||
पर = 2एक्स + 5. |
पर = 2एक्स – 5. |
||
पर= 4cos एक्स. |
पर= 3पाप एक्स. |
||
पर= टीजी एक्स+सीटीजी एक्स. |
पर= टीजी एक्स-सीटीजी एक्स. |
||
पर= पाप 3 एक्स. |
पर= क्योंकि 4 एक्स. |
||
उत्तर विकल्प. |
|||
– 4 पाप एक्स |
– 3cos एक्स |
||
1/cos 2 एक्स+1/पाप 2 एक्स |
1/cos 2 एक्स–1/पाप 2 एक्स |
1/पाप 2 एक्स–1/cos 2 एक्स |
|
– 4sin4 एक्स |
– 3cos3 एक्स |
||
नोटबुक का आदान-प्रदान करें। डायग्नोस्टिक कार्ड में, सही ढंग से पूर्ण किए गए कार्यों को + चिह्न के साथ चिह्नित करें, और गलत तरीके से पूर्ण किए गए कार्यों को - चिह्न के साथ चिह्नित करें।
चतुर्थ. व्युत्पन्न का उपयोग करके समीकरणों को हल करना
- उन बिंदुओं को कैसे खोजें जिन पर व्युत्पन्न शून्य है?
उन बिंदुओं को खोजने के लिए जिन पर व्युत्पन्न है यह फ़ंक्शनशून्य के बराबर, आपको चाहिए:
- फ़ंक्शन की प्रकृति निर्धारित करें,
- क्षेत्र खोजें फ़ंक्शन परिभाषाएँ,
- इस फ़ंक्शन का व्युत्पन्न खोजें,
- प्रश्न हल करें एफ "(एक्स) = 0,
- सही उत्तर का चयन करें।
कार्य 1।
दिया गया: पर
= एक्स-पाप एक्स.
खोजो:जिन बिंदुओं पर व्युत्पन्न शून्य है।
समाधान।फ़ंक्शन सभी वास्तविक संख्याओं के सेट पर परिभाषित और भिन्न होता है, क्योंकि फ़ंक्शन सभी वास्तविक संख्याओं के सेट पर परिभाषित और भिन्न होता है जी(एक्स) = एक्सऔर टी(एक्स)=-पाप एक्स.
विभेदीकरण नियमों का उपयोग करते हुए, हम प्राप्त करते हैं एफ
"(एक्स) = (एक्स-पाप एक्स)" = (एक्स)"- (पाप एक्स)" = 1 – क्योंकि एक्स.
अगर एफ "(एक्स) = 0, फिर 1 – कॉस एक्स = 0.
ओल एक्स= 1/; आइए हर में अतार्किकता से छुटकारा पाएं, हमें क्योंकि मिलता है एक्स
= /2.
सूत्र के अनुसार टी= ± आर्ककोस ए+ 2एन, एनजेड, हमें मिलता है: एक्स= ± आर्ककोस /2 + 2एन, एन जेड।
उत्तर: x = ± /4 + 2n, n Z.
V. एल्गोरिथम का उपयोग करके समीकरणों को हल करना
पता लगाएं कि किन बिंदुओं पर व्युत्पन्न गायब हो जाता है।
एफ(एक्स) = पाप एक्स+क्योंकि एक्स |
एफ(एक्स) = पाप 2 एक्स – एक्स |
एफ(एक्स) = 2एक्स+क्योंकि(4 एक्स – ) |
छात्र तीन उदाहरणों में से कोई भी चुन सकता है। पहला उदाहरण रेट किया गया है " 3 ", दूसरा - " 4 ", तीसरा - " 5 " आपसी जाँच के बाद नोटबुक में समाधान। एक छात्र बोर्ड में निर्णय लेता है। यदि समाधान गलत हो जाता है, तो छात्र को एल्गोरिदम पर वापस लौटना होगा और फिर से हल करने का प्रयास करना होगा।
क्रमादेशित नियंत्रण.
विकल्प 1 |
विकल्प 2 |
|||
य = 2एक्स 3 |
य = 3एक्स 2 |
|||
य = 1/4 एक्स 4 + 2एक्स 2 – 7 |
य = 1/2 एक्स 4 + 4एक्स + 5 |
|||
य = एक्स 3 + 4एक्स 2
– 3एक्स. |
य = 2एक्स 3 – 9एक्स 2
+ 12एक्स + 7. |
|||
य= पाप 2 एक्स– क्योंकि 3 एक्स. |
य= क्योंकि 2 एक्स– पाप 3 एक्स. |
|||
य= टीजी एक्स-सीटीजी( एक्स + /4). |
य=ctg एक्स+ टीजी( एक्स – /4). |
|||
य= पाप 2 एक्स. |
य= क्योंकि 2 एक्स. |
|||
उत्तर विकल्प. |
||||
|
| ||||








