HOMOGĒNO LINEĀRO VIENĀDĀJUMU SISTĒMA
Viendabīga sistēma lineārie vienādojumi sauc par formu sistēmu
Skaidrs, ka šajā gadījumā 
, jo visi vienas kolonnas elementi šajos determinantos ir vienādi ar nulli.
Tā kā nezināmie tiek atrasti pēc formulām 
, tad gadījumā, ja Δ ≠ 0, sistēmai ir unikāls nulles risinājums x = y = z= 0. Tomēr daudzās problēmās interesants ir jautājums, vai viendabīga sistēma risinājumi, kas nav nulles.
Teorēma. Lai lineārajai sistēmai viendabīgi vienādojumi bija risinājums, kas nav nulle, ir nepieciešams un pietiekami, lai Δ ≠ 0.
Tātad, ja determinants Δ ≠ 0, tad sistēmai ir unikāls risinājums. Ja Δ ≠ 0, tad lineāro viendabīgo vienādojumu sistēmai ir bezgalīgs atrisinājumu skaits.
Piemēri.
Matricas īpašvektori un īpatnējās vērtības
Dota kvadrātveida matrica 
, X– kāda matrica-kolonna, kuras augstums sakrīt ar matricas secību A. .
Daudzās problēmās mums ir jāņem vērā vienādojums X
kur λ ir noteikts skaitlis. Ir skaidrs, ka jebkuram λ šim vienādojumam ir nulles risinājums.
Tiek izsaukts skaitlis λ, kuram šim vienādojumam ir nulles atrisinājumi īpašvērtība matricas A, A X par šādu λ sauc īpašvektors matricas A.
Atradīsim matricas īpašvektoru A. Jo E∙X = X, tad matricas vienādojumu var pārrakstīt kā 
vai 
. Izvērstā formā šo vienādojumu var pārrakstīt kā lineāru vienādojumu sistēmu. Tiešām 
.
Un tāpēc 
Tātad, mēs esam ieguvuši viendabīgu lineāru vienādojumu sistēmu koordinātu noteikšanai x 1, x 2, x 3 vektors X. Lai sistēmai būtu risinājumi, kas atšķiras no nulles, ir nepieciešams un pietiekami, lai sistēmas determinants būtu vienāds ar nulli, t.i.
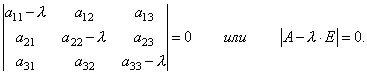
Šis ir λ trešās pakāpes vienādojums. To sauc raksturīgais vienādojums matricas A un kalpo λ īpašvērtību noteikšanai.
Katra īpašvērtība λ atbilst īpašvektoram X, kuras koordinātas tiek noteiktas no sistēmas pie atbilstošās λ vērtības.
Piemēri.
VEKTORS ALGEBRA. VEKTORA JĒDZIENS
Pētot dažādas fizikas nozares, ir lielumi, kurus pilnībā nosaka, norādot to skaitliskās vērtības, piemēram, garumu, laukumu, masu, temperatūru u.c. Šādus lielumus sauc par skalāriem. Taču papildus tiem ir arī lielumi, kuru noteikšanai papildus skaitliskajai vērtībai ir jāzina arī to virziens telpā, piemēram, spēks, kas iedarbojas uz ķermeni, kustības ātrums un paātrinājums. ķermenis, kad tas pārvietojas telpā, spriedze magnētiskais lauks noteiktā telpas punktā utt. Šādus lielumus sauc par vektora lielumiem.
Ieviesīsim stingru definīciju.
Režisēts segments Sauksim segmentu, attiecībā pret kura galiem ir zināms, kurš no tiem ir pirmais un kurš otrais.
Vektors sauc par virzītu segmentu ar noteiktu garumu, t.i. Šis ir noteikta garuma segments, kurā viens no to ierobežojošajiem punktiem tiek ņemts par sākumu, bet otrs - kā beigas. Ja A- vektora sākums, B ir tā beigas, tad vektoru apzīmē ar simbolu, turklāt vektoru bieži apzīmē ar vienu burtu. Attēlā vektors ir norādīts ar segmentu, bet tā virziens ar bultiņu.
Modulis vai garums Vektoru sauc par virzītā segmenta garumu, kas to nosaka. Apzīmē ar || vai ||.
Kā vektorus iekļausim arī tā saukto nulles vektoru, kura sākums un beigas sakrīt. Tas ir norādīts. Nulles vektoram nav noteikta virziena, un tā modulis ir nulle ||=0.
Vektorus sauc kolineārs, ja tie atrodas uz vienas līnijas vai uz paralēlām līnijām. Turklāt, ja vektori un atrodas vienā virzienā, mēs rakstīsim , pretēji.
Tiek saukti vektori, kas atrodas uz taisnēm, kas ir paralēlas tai pašai plaknei koplanārs.
Abi vektori tiek saukti vienāds, ja tie ir kolineāri, tiem ir vienāds virziens un vienāds garums. Šajā gadījumā viņi raksta.
No vektoru vienādības definīcijas izriet, ka vektoru var transportēt paralēli sev, novietojot tā sākumu jebkurā telpas punktā.
Piemēram.
LINEĀRAS OPERĀCIJAS UZ VEKTORIEM
- Vektora reizināšana ar skaitli.
Vektora un skaitļa λ reizinājums ir jauns vektors, kurā:
Vektora un skaitļa λ reizinājumu apzīmē ar .
Piemēram, ir vektors, kas ir vērsts tajā pašā virzienā kā vektors un kura garums ir uz pusi mazāks nekā vektora garums.
Ieviestajai darbībai ir sekojošs īpašības:
- Vektoru pievienošana.
Ļaut un ir divi patvaļīgi vektori. Ņemsim patvaļīgu punktu O un izveidojiet vektoru. Pēc tam no punkta A noliksim malā vektoru. Tiek izsaukts vektors, kas savieno pirmā vektora sākumu ar otrā vektora beigām summa no šiem vektoriem un ir apzīmēts
.
Tiek saukta formulētā vektoru saskaitīšanas definīcija paralelograma noteikums, jo vienu un to pašu vektoru summu var iegūt šādi. Atliksim no punkta O vektori un . Konstruēsim uz šiem vektoriem paralelogramu OABC. Tā kā vektori, tad vektors, kas ir no virsotnes novilkta paralelograma diagonāle O, acīmredzot būs vektoru summa.
Ir viegli pārbaudīt tālāk norādīto vektoru pievienošanas īpašības.
- Vektoru atšķirība.
Tiek izsaukts vektors, kas ir kolineārs noteiktam vektoram, vienāda garuma un pretējā virzienā pretī vektors vektoram un tiek apzīmēts ar . Pretējo vektoru var uzskatīt par vektora reizināšanas ar skaitli λ = –1 rezultātu: .
Definīcija 9.3. Vektors X sauca īpašvektors matricas A, ja tāds skaitlis ir λ, ka vienlīdzība ir spēkā: A X= λ X, tas ir, pieteikšanās rezultāts uz X lineārā transformācija, ko nosaka matrica A, ir šī vektora reizinājums ar skaitli λ . Pats numurs λ sauca īpašvērtība matricas A.
Aizstāšana ar formulām (9.3.) x` j = λx j , iegūstam vienādojumu sistēmu īpašvektora koordinātu noteikšanai:
. (9.5)
Šai lineārajai viendabīgai sistēmai būs netriviāls risinājums tikai tad, ja tās galvenais determinants ir 0 (Krāmera likums). Ierakstot šo nosacījumu formā:
iegūstam vienādojumu īpašvērtību noteikšanai λ , zvanīja raksturīgais vienādojums. Īsumā to var attēlot šādi:
| A - λE | = 0, (9.6)
jo tā kreisajā pusē ir matricas determinants A-λE. Polinoma radinieks λ | A - λE| sauca raksturīgs polinoms matricas A.
Raksturīgā polinoma īpašības:
1) Lineāras transformācijas raksturīgais polinoms nav atkarīgs no bāzes izvēles. Pierādījums. 
(sk. (9.4)), bet 
tātad,. Tādējādi tas nav atkarīgs no bāzes izvēles. Tas nozīmē, ka | A-λE| nemainās, pārejot uz jaunu pamatu.
2) Ja matrica A lineārā transformācija ir simetrisks(tie. un ij =a ji), tad visas raksturīgā vienādojuma (9.6) saknes ir reāli skaitļi.
Īpašvērtību un īpašvektoru īpašības:
1) Ja izvēlaties bāzi no īpašvektoriem x 1, x 2, x 3 , kas atbilst īpašvērtībām λ 1, λ 2, λ 3 matricas A, tad šajā pamatā lineārajai transformācijai A ir diagonālas formas matrica:
(9.7) Šīs īpašības pierādījums izriet no īpašvektoru definīcijas.
2) Ja transformācijas īpašvērtības A ir atšķirīgi, tad tiem atbilstošie īpašvektori ir lineāri neatkarīgi.
3) Ja matricas raksturīgais polinoms A ir trīs dažādas saknes, tad kaut kādā veidā matrica A ir diagonāls izskats.
Atradīsim matricas īpašvērtības un īpašvektorus raksturīgais vienādojums: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7 λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
Atradīsim katrai atrastajai vērtībai atbilstošo īpašvektoru koordinātas λ. No (9.5) izriet, ka ja X (1) ={x 1, x 2, x 3) – atbilstošs īpašvektors λ 1 =-2, tad
- kooperatīva, bet nenoteikta sistēma. Tās risinājumu var ierakstīt formā X (1)
={a,0,-a), kur a ir jebkurš skaitlis. Jo īpaši, ja mēs to prasām | x (1)
|=1, X (1)
=
Aizstāšana sistēmā (9.5.) λ 2 =3, iegūstam otrā īpašvektora koordinātu noteikšanas sistēmu - x (2) ={y 1 ,y 2 ,y 3}:
, kur X (2)
={b,-b,b) vai, ja | x (2)
|=1, x (2)
= 
Par λ 3 = 6 atrodiet īpašvektoru x (3) ={z 1 , z 2 , z 3}:
, x (3)
={c,2c,c) vai normalizētajā versijā
x (3) = 
To var pamanīt X (1) X (2)
= ab–ab= 0, x (1) x (3)
= ac-ac= 0, x (2) x (3)
= bc- 2bc + bc= 0. Tādējādi šīs matricas īpašvektori ir pa pāriem ortogonāli.
10. lekcija.
Kvadrātformas un to saistība ar simetriskām matricām. Simetriskas matricas īpašvektoru un īpašvērtību īpašības. Kvadrātiskās formas reducēšana uz kanonisko formu.
Definīcija 10.1.Kvadrātiskā forma reāli mainīgie x 1, x 2,…, x n tiek saukts par otrās pakāpes polinomu šajos mainīgajos, kas nesatur brīvo terminu un pirmās pakāpes terminus.
Kvadrātisko formu piemēri:
(n = 2),
(n = 3). (10.1)
Atcerēsimies simetriskas matricas definīciju, kas sniegta pēdējā lekcijā:
Definīcija 10.2. Tiek saukta kvadrātveida matrica simetrisks, ja , tas ir, ja matricas elementi, kas ir simetriski galvenajai diagonālei, ir vienādi.
Simetriskas matricas īpašvērtību un īpašvektoru īpašības:
1) Visas simetriskas matricas īpašvērtības ir reālas.
Pierādījums (par n = 2).
Ļaujiet matricai A ir šāda forma: 
. Izveidosim raksturīgo vienādojumu:
(10.2) Atradīsim diskriminantu:
Tāpēc vienādojumam ir tikai reālas saknes.
2) Pašvektori simetriskās matricas ir ortogonālas.
Pierādījums (par n= 2).
Īpašvektoru un koordinātām ir jāatbilst vienādojumiem.
www.vietneļauj atrast. Vietne veic aprēķinu. Pēc dažām sekundēm serveris sniegs pareizo risinājumu. Matricai raksturīgais vienādojums būs algebriskā izteiksme, ko nosaka determinanta aprēķināšanas noteikums matricas matricas, savukārt gar galveno diagonāli būs atšķirības diagonālo elementu un mainīgā vērtībās. Aprēķinot raksturīgs vienādojums matricai tiešsaistē, katrs elements matricas tiks reizināts ar atbilstošiem citiem elementiem matricas. Atrast režīmā tiešsaistē iespējams tikai kvadrātā matricas. Meklēšanas operācija raksturīgs vienādojums matricai tiešsaistē samazina līdz elementu reizinājuma algebriskās summas aprēķināšanai matricas noteicēja atrašanas rezultātā matricas, tikai ar mērķi noteikt raksturīgs vienādojums matricai tiešsaistē. Šī operācija teorētiski ieņem īpašu vietu matricas, ļauj atrast īpašvērtības un vektorus, izmantojot saknes. Uzdevums atrast raksturīgs vienādojums matricai tiešsaistē sastāv no vairojošiem elementiem matricas kam seko šo produktu summēšana saskaņā ar noteiktu noteikumu. www.vietne atrod matricas raksturīgo vienādojumu dotā dimensija režīmā tiešsaistē. Aprēķins raksturīgs vienādojums matricai tiešsaistēņemot vērā tā dimensiju, tas ir polinoma atrašana ar skaitliskiem vai simboliskiem koeficientiem, kas atrasti saskaņā ar determinanta aprēķināšanas noteikumu matricas- kā atbilstošo elementu reizinājumu summa matricas, tikai ar mērķi noteikt raksturīgs vienādojums matricai tiešsaistē. Polinoma atrašana attiecībā pret kvadrātveida mainīgo matricas, kā definīcija matricas raksturīgo vienādojumu, teorētiski izplatīts matricas. Polinoma sakņu nozīme raksturīgs vienādojums matricai tiešsaistē izmanto, lai noteiktu īpašvektorus un īpašvērtības matricas. Turklāt, ja noteicošais matricas būs vienāds ar nulli, tad matricas raksturīgais vienādojums joprojām pastāvēs, atšķirībā no otrādi matricas. Lai aprēķinātu matricas raksturīgo vienādojumu vai atrodiet vairākus uzreiz matricu raksturīgie vienādojumi, jums jāpavada daudz laika un pūļu, savukārt mūsu serveris atradīs dažu sekunžu laikā raksturīgs vienādojums matricai tiešsaistē. Šajā gadījumā atbilde uz atrašanu raksturīgs vienādojums matricai tiešsaistē būs pareizi un ar pietiekamu precizitāti, pat ja skaitļus atrodot raksturīgs vienādojums matricai tiešsaistē būs neracionāli. Vietnē www.vietne rakstzīmju ieraksti ir atļauti elementos matricas, tas ir raksturīgs vienādojums matricai tiešsaistē aprēķinot var attēlot vispārīgā simboliskā formā matricas raksturīgs vienādojums tiešsaistē. Iegūto atbildi ir lietderīgi pārbaudīt, risinot atrašanas problēmu raksturīgs vienādojums matricai tiešsaistē izmantojot vietni www.vietne. Veicot polinoma aprēķināšanas operāciju - matricas raksturīgais vienādojums, jums jābūt uzmanīgam un ļoti koncentrētam, risinot šo problēmu. Savukārt mūsu vietne palīdzēs jums pārbaudīt jūsu lēmumu par tēmu matricas raksturīgs vienādojums tiešsaistē. Ja jums nav laika ilgstoši pārbaudīt atrisinātās problēmas, tad www.vietne noteikti būs ērts rīks pārbaudei, atrodot un aprēķinot raksturīgs vienādojums matricai tiešsaistē.
Kvadrātveida matricas īpašvektors ir tāds, kas, reizinot ar doto matricu, rada kolineāru vektoru. Vienkāršiem vārdiem sakot, reizinot matricu ar īpašvektoru, pēdējais paliek nemainīgs, bet reizināts ar noteiktu skaitli.
Definīcija
Īpatnējs vektors ir vektors V, kas atšķiras no nulles, kurš, reizinot ar kvadrātmatricu M, pats kļūst palielināts ar kādu skaitli λ. Algebriskajā apzīmējumā tas izskatās šādi:
M × V = λ × V,
kur λ ir matricas M īpašvērtība.
Apsvērsim skaitlisks piemērs. Lai atvieglotu ierakstīšanu, skaitļi matricā tiks atdalīti ar semikolu. Ļaujiet mums izveidot matricu:
- M = 0; 4;
- 6; 10.
Sareizināsim to ar kolonnas vektoru:
- V = -2;
Reizinot matricu ar kolonnas vektoru, mēs iegūstam arī kolonnas vektoru. Stingri matemātiskā valoda formula 2 × 2 matricas reizināšanai ar kolonnas vektoru izskatītos šādi:
- M × V = M11 × V11 + M12 × V21;
- M21 × V11 + M22 × V21.
M11 ir matricas M elements, kas atrodas pirmajā rindā un pirmajā kolonnā, un M22 ir elements, kas atrodas otrajā rindā un otrajā kolonnā. Mūsu matricai šie elementi ir vienādi ar M11 = 0, M12 = 4, M21 = 6, M22 10. Kolonnas vektoram šīs vērtības ir vienādas ar V11 = –2, V21 = 1. Saskaņā ar šo formulu, mēs iegūstam šādu kvadrātmatricas reizinājuma rezultātu ar vektoru:
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
Ērtības labad ierakstīsim kolonnas vektoru rindā. Tātad, mēs reizinām kvadrātveida matricu ar vektoru (-2; 1), iegūstot vektoru (4; -2). Acīmredzot tas ir tas pats vektors, kas reizināts ar λ = -2. Lambda iekšā šajā gadījumā apzīmē matricas īpašvērtību.
Matricas īpašvektors ir kolineārs vektors, tas ir, objekts, kas nemaina savu pozīciju telpā, reizinot ar matricu. Kolinearitātes jēdziens vektoru algebrā ir līdzīgs paralēlisma terminam ģeometrijā. Ģeometriskā interpretācijā kolineārie vektori ir dažāda garuma paralēli virzīti segmenti. Kopš Eiklida laikiem mēs zinām, ka vienai taisnei ir bezgalīgs skaits tai paralēlu līniju, tāpēc ir loģiski pieņemt, ka katrai matricai ir bezgalīgs skaits īpašvektoru.
No iepriekšējā piemēra ir skaidrs, ka īpašvektori var būt (-8; 4), un (16; -8) un (32, -16). Tie visi ir kolineārie vektori, kas atbilst īpašvērtībai λ = -2. Reizinot sākotnējo matricu ar šiem vektoriem, mēs tik un tā iegūsim vektoru, kas no sākotnējās atšķiras 2 reizes. Tāpēc, risinot īpašvektora atrašanas uzdevumus, ir jāatrod tikai lineāri neatkarīgi vektoru objekti. Visbiežāk n × n matricai ir n skaits īpašvektoru. Mūsu kalkulators ir paredzēts otrās kārtas kvadrātveida matricu analīzei, tāpēc gandrīz vienmēr rezultāts atradīs divus īpašvektorus, izņemot gadījumus, kad tie sakrīt.
Iepriekš minētajā piemērā mēs iepriekš zinājām sākotnējās matricas īpašvektoru un skaidri noteicām lambda skaitli. Tomēr praksē viss notiek otrādi: vispirms tiek atrastas īpašvērtības un tikai pēc tam īpašvektori.
Risinājuma algoritms
Apskatīsim vēlreiz sākotnējo matricu M un mēģināsim atrast abus tās īpašvektorus. Tātad matrica izskatās šādi:
- M = 0; 4;
- 6; 10.
Vispirms mums ir jānosaka īpašvērtība λ, kam nepieciešams aprēķināt šādas matricas determinantu:
- (0 - λ); 4;
- 6; (10 − λ).
Šo matricu iegūst, atņemot nezināmo λ no elementiem galvenajā diagonālē. Determinantu nosaka, izmantojot standarta formulu:
- detA = M11 × M21 - M12 × M22
- detA = (0 − λ) × (10 − λ) − 24
Tā kā mūsu vektoram nav jābūt nullei, mēs pieņemam iegūto vienādojumu kā lineāri atkarīgu un pielīdzinām mūsu determinantu detA ar nulli.
(0 − λ) × (10 − λ) − 24 = 0
Atvērsim iekavas un iegūstam matricas raksturīgo vienādojumu:
λ 2 - 10 λ - 24 = 0
Tas ir standarts kvadrātvienādojums, kas jāatrisina, izmantojot diskriminantu.
D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196
Diskriminanta sakne ir sqrt(D) = 14, tāpēc λ1 = -2, λ2 = 12. Tagad katrai lambda vērtībai jāatrod īpašvektors. Izteiksim sistēmas koeficientus λ = -2.
- M – λ × E = 2; 4;
- 6; 12.
Šajā formulā E ir identitātes matrica. Pamatojoties uz iegūto matricu, mēs izveidojam lineāro vienādojumu sistēmu:
2x + 4g = 6x + 12g,
kur x un y ir īpašvektora elementi.
Apkoposim visus X kreisajā pusē un visus Y labajā pusē. Acīmredzot - 4x = 8g. Sadaliet izteiksmi ar - 4 un iegūstiet x = -2y. Tagad mēs varam noteikt pirmo matricas īpašvektoru, ņemot jebkuras nezināmo vērtības (atcerieties lineāri atkarīgo īpašvektoru bezgalību). Pieņemsim, ka y = 1, tad x = –2. Tāpēc pirmais īpašvektors izskatās kā V1 = (–2; 1). Atgriezties uz raksta sākumu. Tieši ar šo vektora objektu mēs reizinājām matricu, lai parādītu īpašvektora jēdzienu.
Tagad atradīsim īpašvektoru λ = 12.
- M - λ × E = -12; 4
- 6; -2.
Izveidosim tādu pašu lineāro vienādojumu sistēmu;
- -12x + 4y = 6x - 2y
- -18x = -6 gadi
- 3x = y.
Tagad mēs ņemam x = 1, tāpēc y = 3. Tādējādi otrais īpašvektors izskatās kā V2 = (1; 3). Reizinot sākotnējo matricu ar doto vektoru, rezultāts vienmēr būs tas pats vektors, kas reizināts ar 12. Šeit beidzas risinājuma algoritms. Tagad jūs zināt, kā manuāli noteikt matricas īpašvektoru.
- noteicējs;
- izsekot, tas ir, elementu summa galvenajā diagonālē;
- rangs, tas ir, maksimālais lineāri neatkarīgo rindu/kolonnu skaits.
Programma darbojas pēc iepriekšminētā algoritma, pēc iespējas saīsinot risinājuma procesu. Svarīgi norādīt, ka programmā lambda tiek apzīmēta ar burtu “c”. Apskatīsim skaitlisko piemēru.
Programmas darbības piemērs
Mēģināsim noteikt īpašvektorus šādai matricai:
- M = 5; 13;
- 4; 14.
Ievadīsim šīs vērtības kalkulatora šūnās un saņemsim atbildi šādā formā:
- Matricas rangs: 2;
- Matricas determinants: 18;
- Matricas trase: 19;
- Īpašvektora aprēķins: c 2 − 19,00c + 18,00 (raksturojošs vienādojums);
- Pašvektora aprēķins: 18 (pirmā lambda vērtība);
- Pašvektora aprēķins: 1 (otrā lambda vērtība);
- Vienādojumu sistēma vektoram 1: -13x1 + 13y1 = 4x1 − 4y1;
- Vienādojumu sistēma vektoram 2: 4x1 + 13y1 = 4x1 + 13y1;
- 1. pašvektors: (1; 1);
- 2. īpašvektors: (-3,25; 1).
Tādējādi mēs ieguvām divus lineāri neatkarīgus īpašvektorus.
Secinājums
Lineārā algebra un analītiskā ģeometrija ir standarta priekšmeti jebkuram inženierzinātņu pirmkursniekam. Lielais vektoru un matricu skaits ir biedējošs, un šādos apgrūtinošos aprēķinos ir viegli kļūdīties. Mūsu programma ļaus studentiem pārbaudīt savus aprēķinus vai automātiski atrisināt īpašvektora atrašanas problēmu. Mūsu katalogā ir arī citi lineārās algebras kalkulatori, kurus varat izmantot mācībās vai darbā.
