Szczególne znaczenie dla charakterystyki rozkładu zmiennej losowej mają charakterystyki numeryczne zwane momentami początkowymi i centralnymi.
Moment początkowy k-ta kolejność α k(X) zmienna losowa X k-ta potęga tej wielkości, tj.
α k(X) = M(X k) (6.8)
Wzór (6.8) ze względu na definicję oczekiwań matematycznych dla różnych zmienne losowe ma swoją postać, a mianowicie dyskretnej zmiennej losowej o skończonym zbiorze wartości
dla ciągłej zmiennej losowej
 , (6.10)
, (6.10)
Gdzie F(X) - gęstość rozkładu zmiennej losowej X.
Niewłaściwa integralność we wzorze (6.10) zamienia się w określona całka w skończonym przedziale, jeśli wartości ciągłej zmiennej losowej istnieją tylko w tym przedziale.
Jedną z wcześniej wprowadzonych charakterystyk numerycznych jest wartość oczekiwana- to nic innego jak początkowy moment pierwszego rzędu, czyli, jak mówią, pierwszy moment początkowy:
M(X) = α 1 (X).
W poprzednim akapicie wprowadzono koncepcję wycentrowanej zmiennej losowej HM(X). Jeśli tę wielkość uznamy za główną, wówczas można dla niej znaleźć również momenty początkowe. Dla samej wielkości X te momenty będą nazywane centralnymi.
Centralny moment k-ta kolejność μk(X) zmienna losowa X zwane oczekiwaniami matematycznymi k-ta potęga wyśrodkowanej zmiennej losowej, tj.
μk(X) = M[(HM(X))k] (6.11)
Inaczej mówiąc, punkt centralny k-ty rząd to oczekiwanie matematyczne k stopień odchylenia.
Centralny moment k rząd dla dyskretnej zmiennej losowej o skończonym zbiorze wartości wyznacza się ze wzoru:
![]() , (6.12)
, (6.12)
dla ciągłej zmiennej losowej korzystając ze wzoru:
 (6.13)
(6.13)
W przyszłości, gdy będzie już jasne, o jakim rodzaju zmiennej losowej mówimy, nie będziemy jej pisać w zapisie dla momentów początkowych i centralnych, tj. zamiast α k(X) I μk(X) po prostu napiszemy α k I μk .
Oczywiste jest, że moment centralny pierwszego rzędu jest równy zeru, ponieważ jest to nic innego jak matematyczne oczekiwanie odchylenia, które jest równe zeru zgodnie z tym, co zostało wcześniej udowodnione, tj. .
Nietrudno zrozumieć, że moment centralny drugiego rzędu zmiennej losowej X pokrywa się z wariancją tej samej zmiennej losowej, tj.
Ponadto istnieją następujące wzory łączące momenty początkowy i centralny:

Zatem momenty pierwszego i drugiego rzędu (oczekiwanie matematyczne i dyspersja) charakteryzują się najbardziej Ważne cechy rozkład: jego położenie i stopień rozproszenia wartości. Aby uzyskać więcej szczegółowy opis rozkłady są momentami wyższego rzędu. Pokażmy to.
Załóżmy, że rozkład zmiennej losowej jest symetryczny względem jej oczekiwań matematycznych. Wtedy wszystkie momenty centralne nieparzystego rzędu, jeśli istnieją, są równe zeru. Wyjaśnia to fakt, że ze względu na symetrię rozkładu dla każdej dodatniej wartości wielkości X − M(X) istnieje wartość ujemna równa jej wielkości, a prawdopodobieństwa tych wartości są równe. W rezultacie suma we wzorze (6.12) składa się z kilku par wyrazów równych co do wielkości, ale różniących się znakiem, które po zsumowaniu znoszą się. Tym samym cała kwota, tj. centralny moment dowolnej dyskretnej zmiennej losowej rzędu nieparzystego wynosi zero. Podobnie moment centralny dowolnego rzędu nieparzystego ciągłej zmiennej losowej jest równy zeru, podobnie jak całka w granicach symetrycznych funkcji nieparzystej.
Naturalnym jest założenie, że jeśli moment centralny rzędu nieparzystego jest różny od zera, to sam rozkład nie będzie symetryczny względem jego oczekiwań matematycznych. Co więcej, im bardziej moment centralny różni się od zera, tym większa jest asymetria w rozkładzie. Przyjmijmy centralny moment najmniejszego rzędu nieparzystego jako cechę asymetrii. Ponieważ moment centralny pierwszego rzędu wynosi zero dla zmiennych losowych o dowolnym rozkładzie, lepiej jest w tym celu wykorzystać moment centralny trzeciego rzędu. Jednak moment ten ma wymiar sześcianu zmiennej losowej. Aby pozbyć się tej wady i przejść do bezwymiarowej zmiennej losowej, należy podzielić wartość momentu centralnego przez sześcian odchylenia standardowego.
Współczynnik asymetrii Jak lub po prostu asymetria nazywa się stosunkiem centralnego momentu trzeciego rzędu do sześcianu odchylenia standardowego, tj.
Czasami asymetria nazywana jest „skośnością” i jest określana Sk z czego pochodzi angielskie słowo pochylić - „ukośny”.
Jeżeli współczynnik asymetrii jest ujemny, to na jego wartość duży wpływ mają składniki ujemne (odchylenia) i rozkład będzie miał lewa asymetria, a wykres rozkładu (krzywa) jest bardziej płaski na lewo od oczekiwań matematycznych. Jeśli współczynnik jest dodatni, to asymetria, prawda, a krzywa jest bardziej płaska na prawo od oczekiwań matematycznych (ryc. 6.1).
 |
Jak pokazano, do scharakteryzowania rozrzutu wartości zmiennej losowej wokół jej matematycznej wartości oczekiwanej wykorzystuje się drugi moment centralny, tj. dyspersja. Jeśli ten moment jest bardzo ważny wartość numeryczna, to ta zmienna losowa ma duży rozrzut wartości i odpowiadająca jej krzywa rozkładu ma bardziej płaski kształt niż krzywa, dla której drugi moment centralny ma mniejszą wartość. Dlatego drugi moment centralny charakteryzuje w pewnym stopniu krzywą rozkładu o „płaskim” lub „ostrym wierzchołku”. Jednak ta cecha nie jest zbyt wygodna. Moment centralny drugiego rzędu ma wymiar równy kwadratowi wymiary zmiennej losowej. Jeśli spróbujemy otrzymać wielkość bezwymiarową dzieląc wartość momentu przez kwadrat odchylenia standardowego, to dla dowolnej zmiennej losowej otrzymamy: ![]() . Zatem współczynnik ten nie może być żadną cechą rozkładu zmiennej losowej. To samo dotyczy wszystkich dystrybucji. W tym przypadku można zastosować moment centralny czwartego rzędu.
. Zatem współczynnik ten nie może być żadną cechą rozkładu zmiennej losowej. To samo dotyczy wszystkich dystrybucji. W tym przypadku można zastosować moment centralny czwartego rzędu.
Nadmiar Ek jest ilością określoną ze wzoru
![]() (6.15)
(6.15)
Kurtoza jest stosowana głównie w przypadku ciągłych zmiennych losowych i służy do scharakteryzowania tzw. „stromości” krzywej rozkładu lub inaczej, jak już wspomniano, do scharakteryzowania krzywej rozkładu o „płaskim wierzchołku” lub „ostrym wierzchołku”. Krzywą rozkładu odniesienia uważa się za krzywą normalna dystrybucja(zostanie to szczegółowo omówione w następnym rozdziale). W przypadku zmiennej losowej o rozkładzie zgodnym z prawem normalnym zachodzi równość. Zatem kurtoza określona wzorem (6.15) służy porównaniu tego rozkładu z rozkładem normalnym, dla którego kurtoza jest równa zeru.
Jeśli dla jakiejś zmiennej losowej uzyska się dodatnią kurtozę, to krzywa rozkładu tej wartości jest bardziej szczytowa niż krzywa rozkładu normalnego. Jeżeli kurtoza jest ujemna, wówczas krzywa ma bardziej płaski wierzchołek w porównaniu z krzywą rozkładu normalnego (ryc. 6.2).
 |
Przejdźmy teraz do konkretnych typów praw rozkładu dla dyskretnych i ciągłych zmiennych losowych.
Oprócz charakterystyk pozycji - średnich, typowych wartości zmiennej losowej - stosuje się szereg cech, z których każda opisuje jedną lub drugą właściwość rozkładu. Jako takie cechy najczęściej wykorzystuje się tzw. momenty.
Pojęcie momentu jest szeroko stosowane w mechanice do opisu rozkładu mas (momenty statyczne, momenty bezwładności itp.). Dokładnie te same techniki są stosowane w teorii prawdopodobieństwa do opisu podstawowych właściwości rozkładu zmiennej losowej. Najczęściej w praktyce stosuje się dwa rodzaje momentów: początkowy i centralny.
Początkowy moment rzędu nieciągłej zmiennej losowej jest sumą postaci:
 . (5.7.1)
. (5.7.1)
Oczywiście definicja ta pokrywa się z definicją początkowego momentu porządku s w mechanice, jeżeli masy skupiają się w punktach na osi odciętych.
Dla ciągłej zmiennej losowej X początkowy moment s-tego rzędu nazywany jest całką
 . (5.7.2)
. (5.7.2)
Łatwo zauważyć, że główna cecha pozycji wprowadzonej w poprzednim numerze – oczekiwanie matematyczne – to nic innego jak pierwszy moment początkowy zmiennej losowej.
Używając matematycznego znaku oczekiwania, możesz połączyć dwa wzory (5.7.1) i (5.7.2) w jeden. Rzeczywiście, wzory (5.7.1) i (5.7.2) mają całkowicie podobną strukturę do wzorów (5.6.1) i (5.6.2), z tą różnicą, że zamiast i są odpowiednio i . Dlatego możemy napisać ogólną definicję momentu początkowego rzędu th, obowiązującą zarówno dla nieciągłych, jak i ilości ciągłe:
![]() , (5.7.3)
, (5.7.3)
te. Moment początkowy trzeciego rzędu zmiennej losowej jest matematycznym oczekiwaniem trzeciego stopnia tej zmiennej losowej.
Przed zdefiniowaniem momentu centralnego wprowadzamy nową koncepcję „centralnej zmiennej losowej”.
Niech istnieje zmienna losowa z oczekiwaniem matematycznym. Wyśrodkowana zmienna losowa odpowiadająca wartości to odchylenie zmiennej losowej od jej oczekiwań matematycznych:
W przyszłości zgodzimy się na oznaczanie wszędzie wyśrodkowanej zmiennej losowej odpowiadającej danej zmiennej losowej tą samą literą z symbolem u góry.
Łatwo jest sprawdzić, że matematyczne oczekiwanie wyśrodkowanej zmiennej losowej jest równe zero. Rzeczywiście, dla nieciągłej ilości
podobnie dla wielkości ciągłej.
Centrowanie zmiennej losowej jest oczywiście równoznaczne z przesunięciem początku współrzędnych do środkowego, „centralnego” punktu, którego odcięta jest równa oczekiwaniu matematycznemu.
Momenty wyśrodkowanej zmiennej losowej nazywane są momentami centralnymi. Są one analogiczne do momentów wokół środka ciężkości w mechanice.
Zatem centralny moment rzędu s zmiennej losowej jest matematycznym oczekiwaniem th potęgi odpowiedniej wyśrodkowanej zmiennej losowej:
![]() , (5.7.6)
, (5.7.6)
a dla ciągłego – przez całkę
 . (5.7.8)
. (5.7.8)
W dalszej części, w przypadkach, gdy nie ma wątpliwości, do której zmiennej losowej należy dany moment, dla uproszczenia napiszemy po prostu i zamiast i .
Oczywiście dla dowolnej zmiennej losowej moment centralny pierwszego rzędu jest równy zeru:
![]() , (5.7.9)
, (5.7.9)
ponieważ matematyczne oczekiwanie wyśrodkowanej zmiennej losowej jest zawsze równe zero.
Wyprowadźmy relacje łączące momenty centralne i początkowe różnych porządków. Wniosek przeprowadzimy tylko dla ilości nieciągłych; łatwo sprawdzić, że dokładnie te same zależności obowiązują dla wielkości ciągłych, jeśli zastąpimy sumy skończone całkami, a prawdopodobieństwa elementami prawdopodobieństwa.
Rozważmy drugi punkt centralny:

Podobnie dla trzeciego momentu centralnego otrzymujemy:
Wyrażenia dla itp. można uzyskać w podobny sposób.
Zatem dla momentów centralnych dowolnej zmiennej losowej obowiązują wzory:
 (5.7.10)
(5.7.10)
Ogólnie rzecz biorąc, momenty można rozpatrywać nie tylko w odniesieniu do początku (momenty początkowe) lub oczekiwań matematycznych (momenty centralne), ale także w odniesieniu do dowolnego punktu:
![]() . (5.7.11)
. (5.7.11)
Momenty centralne mają jednak przewagę nad wszystkimi innymi: pierwszy moment centralny, jak widzieliśmy, jest zawsze równy zeru, a następny, drugi moment centralny, w tym układzie odniesienia ma wartość minimalną. Udowodnijmy to. Dla nieciągłej zmiennej losowej w wzór (5.7.11) ma postać:
 . (5.7.12)
. (5.7.12)
Przekształćmy to wyrażenie:
Oczywiście wartość ta osiąga minimum, gdy , tj. gdy moment jest rozpatrywany w odniesieniu do punktu.
Ze wszystkich momentów jako charakterystyki zmiennej losowej najczęściej wykorzystuje się pierwszy moment początkowy (oczekiwanie matematyczne) i drugi moment centralny.
Drugi moment centralny nazywany jest wariancją zmiennej losowej. Między innymi ze względu na ogromne znaczenie tej cechy wprowadzamy dla niej specjalne oznaczenie:
Zgodnie z definicją momentu centralnego
te. wariancja zmiennej losowej X jest matematycznym oczekiwaniem kwadratu odpowiedniej zmiennej wyśrodkowanej.
Zastępując wielkość wyrażoną w wyrażeniu (5.7.13) jego wyrażeniem, otrzymujemy również:
![]() . (5.7.14)
. (5.7.14)
Aby bezpośrednio obliczyć wariancję, użyj następujących wzorów:
 , (5.7.15)
, (5.7.15)
 (5.7.16)
(5.7.16)
Odpowiednio dla ilości nieciągłych i ciągłych.
Rozproszenie zmiennej losowej jest cechą dyspersji, rozproszenia wartości zmiennej losowej wokół jej oczekiwań matematycznych. Samo słowo „dyspersja” oznacza „dyspersję”.
Jeśli przejdziemy do mechanicznej interpretacji rozkładu, to rozproszenie to nic innego jak moment bezwładności danego rozkładu masy względem środka ciężkości (oczekiwanie matematyczne).
Wariancja zmiennej losowej ma wymiar kwadratu zmiennej losowej; Aby wizualnie scharakteryzować dyspersję, wygodniej jest użyć wielkości, której wymiar pokrywa się z wymiarem zmiennej losowej. Aby to zrobić, weź pierwiastek kwadratowy z wariancji. Wynikowa wartość nazywana jest odchyleniem standardowym (inaczej „standardowym”) zmiennej losowej. Oznaczymy odchylenie standardowe:
![]() , (5.7.17)
, (5.7.17)
Aby uprościć oznaczenia, często będziemy używać skrótów odchylenia standardowego i dyspersji: i . W przypadku, gdy nie ma wątpliwości, jakiej zmiennej losowej dotyczą te cechy, czasami pominiemy symbol x y i napiszemy po prostu i . Słowa „odchylenie standardowe” będą czasami skracane i zastępowane literami r.s.o.
W praktyce często stosuje się wzór wyrażający rozproszenie zmiennej losowej w jej drugim momencie początkowym (drugi ze wzorów (5.7.10)). W nowym zapisie będzie to wyglądać następująco:
Oczekiwanie i wariancja (lub odchylenie standardowe) to najczęściej używane cechy zmiennej losowej. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. Do bardziej szczegółowego opisu rozkładu wykorzystano momenty wyższych rzędów.
Trzeci centralny punkt służy do scharakteryzowania asymetrii (lub „skośności”) rozkładu. Jeśli rozkład jest symetryczny względem oczekiwań matematycznych (lub, w interpretacji mechanicznej, masa rozkłada się symetrycznie względem środka ciężkości), wówczas wszystkie momenty rzędu nieparzystego (jeśli istnieją) są równe zeru. Rzeczywiście, w sumie

gdy prawo dystrybucji jest symetryczne względem prawa i nieparzyste, każdy wyraz dodatni odpowiada równym całkowita wartość wyraz ujemny, więc cała suma wynosi zero. To samo dotyczy oczywiście całki
 ,
,
która jest równa zeru jako całka w granicach symetrycznych funkcji nieparzystej.
Naturalnym jest zatem wybranie jednego z momentów nieparzystych jako cechy asymetrii rozkładu. Najprostszym z nich jest trzeci moment centralny. Ma wymiar sześcianu zmiennej losowej: aby otrzymać charakterystykę bezwymiarową, trzeci moment dzieli się przez sześcian odchylenia standardowego. Wynikowa wartość nazywana jest „współczynnikiem asymetrii” lub po prostu „asymetrią”; będziemy to oznaczać:
Na ryc. 5.7.1 pokazuje dwa rozkłady asymetryczne; jedna z nich (krzywa I) ma dodatnią asymetrię (); druga (krzywa II) jest ujemna ().

Czwarty centralny punkt służy do scharakteryzowania tzw. „chłodu”, tj. dystrybucja szczytowa lub płaska. Te właściwości rozkładu opisuje się za pomocą tzw. kurtozy. Kurtoza zmiennej losowej jest ilością
Od proporcji odejmujemy liczbę 3 ze względu na bardzo ważne i szeroko rozpowszechnione w przyrodzie prawo rozkładu normalnego (które bliżej poznamy później). Zatem dla rozkładu normalnego kurtoza wynosi zero; krzywe, które są bardziej szczytowe w porównaniu z krzywą normalną, mają dodatnią kurtozę; Krzywe o bardziej płaskich wierzchołkach mają ujemną kurtozę.
Na ryc. Rysunek 5.7.2 przedstawia: rozkład normalny (krzywa I), rozkład z dodatnią kurtozą (krzywa II) i rozkład z ujemną kurtozą (krzywa III).

Oprócz omówionych powyżej momentów początkowych i centralnych, w praktyce czasami stosuje się tzw. momenty absolutne (początkowy i centralny), określone wzorami
Oczywiście momenty absolutne parzystych rzędów pokrywają się z momentami zwykłymi.
Spośród momentów absolutnych najczęściej używany jest pierwszy absolutny moment centralny.
![]() , (5.7.21)
, (5.7.21)
zwane średnim odchyleniem arytmetycznym. Oprócz dyspersji i odchylenia standardowego, jako charakterystykę dyspersji czasami stosuje się odchylenie średnie arytmetyczne.
Oczekiwanie, moda, mediana, momenty początkowe i centralne, a w szczególności dyspersja, odchylenie standardowe, skośność i kurtoza to najczęściej stosowane charakterystyki numeryczne zmiennych losowych. W wielu problemach praktycznych pełna charakterystyka zmienna losowa – prawo dystrybucji – albo nie jest potrzebna, albo nie można jej uzyskać. W takich przypadkach ogranicza się do przybliżonego opisu zmiennej losowej korzystając z pomocy. Charakterystyka liczbowa, z których każda wyraża jakąś charakterystyczną właściwość rozkładu.
Bardzo często charakterystyki liczbowe służą do przybliżonego zastąpienia jednego rozkładu drugim i zwykle starają się dokonać tego zastąpienia w taki sposób, aby kilka ważnych punktów pozostało niezmienionych.
Przykład 1. Przeprowadza się jedno doświadczenie, w wyniku którego może nastąpić zdarzenie, którego prawdopodobieństwo jest równe . Uwzględniana jest zmienna losowa – liczba wystąpień zdarzenia (charakterystyczna zmienna losowa zdarzenia). Określ jego cechy: oczekiwanie matematyczne, rozproszenie, odchylenie standardowe.
Rozwiązanie. Szereg rozkładu wartości ma postać:

gdzie jest prawdopodobieństwo, że zdarzenie nie nastąpi.
Korzystając ze wzoru (5.6.1) znajdujemy matematyczne oczekiwanie wartości:
Rozrzut wartości określa się wzorem (5.7.15):
(Sugerujemy, aby czytelnik uzyskał ten sam wynik, wyrażając rozproszenie w odniesieniu do drugiego momentu początkowego).
Przykład 2. Do tarczy oddano trzy niezależne strzały; Prawdopodobieństwo trafienia każdego strzału wynosi 0,4. zmienna losowa – liczba trafień. Wyznaczanie cech wielkości – oczekiwanie matematyczne, dyspersja, r.s.d., asymetria.
Rozwiązanie. Szereg rozkładu wartości ma postać:

Obliczamy charakterystykę liczbową wielkości.
Moment początkowy k t zamówienie zmienna losowaX X k :
W szczególności,
Centralny moment k t zamówienie zmienna losowaXnazywa się matematycznym oczekiwaniem wielkości k :
 .
(5.11)
.
(5.11)
W szczególności,
Korzystając z definicji i właściwości matematycznego oczekiwania i dyspersji, możemy to uzyskać
 ,
,
 ,
,
Momenty wyższego rzędu są rzadko używane.
Załóżmy, że rozkład zmiennej losowej jest symetryczny względem oczekiwań matematycznych. Wtedy wszystkie centrale nieparzystego rzędu są równe zeru. Można to wytłumaczyć faktem, że dla każdej dodatniej wartości odchylenia X–M[X] przypada (ze względu na symetrię rozkładu) wartość ujemna równa wartości bezwzględnej, a ich prawdopodobieństwa będą takie same. Jeśli moment centralny jest rzędu nieparzystego i nie jest równy zero, oznacza to asymetrię rozkładu i im większy moment, tym większa asymetria. Dlatego najrozsądniej jest przyjąć jakiś dziwny moment centralny jako cechę asymetrii rozkładu. Ponieważ moment centralny pierwszego rzędu jest zawsze równy zero, zaleca się wykorzystanie w tym celu momentu centralnego trzeciego rzędu. Przyjmowanie tego punktu do oceny asymetrii jest jednak niewygodne, ponieważ jego wartość zależy od jednostek, w jakich mierzona jest zmienna losowa. Aby wyeliminować tę wadę, 3 dzieli się przez 3 i uzyskuje w ten sposób charakterystykę.
Współczynnik asymetrii A nazywa się ilością
 .
(5.12)
.
(5.12)

Ryż. 5.1
Jeżeli współczynnik asymetrii jest ujemny, oznacza to duży wpływ na wartość 3 ujemnych odchyleń. W tym przypadku krzywe rozkładu są bardziej płaskie na lewo od M[X]. Jeżeli współczynnik A jest dodatni, wówczas krzywa jest bardziej płaska po prawej stronie.Jak wiadomo, dyspersja (drugi moment centralny) służy do scharakteryzowania rozproszenia wartości zmiennej losowej wokół oczekiwań matematycznych. Im większa dyspersja, tym bardziej płaska jest odpowiednia krzywa rozkładu. Jednak znormalizowany moment drugiego rzędu 2 / 2 nie może służyć jako charakterystyka rozkładu „płaskiego” lub „ostrego”, ponieważ dla dowolnego rozkładu D[ X]/ 2 =1. W tym przypadku stosuje się moment centralny czwartego rzędu.
Nadmiar mi nazywa się ilością
 .
(5.13)
.
(5.13)
H
Ryż. 5.2
Przykład 5.6. DSV X wynika z następującego prawa dystrybucji:
Znajdź współczynnik skośności i kurtozę.
 Ryż. 5.4
Ryż. 5.4




Teraz obliczmy momenty centralne:

Znajdźmy oczekiwanie matematyczne X 2 :
M(X 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.
Widzimy to M(X 2) dużo więcej M(X). Dzieje się tak, ponieważ po podniesieniu do kwadratu możliwe znaczenie wielkie ilości X 2 odpowiadające wartości X= 100 magnitudo X, stał się równy 10 000, tj. znacznie wzrósł; prawdopodobieństwo tej wartości jest niskie (0,01).
Tym samym przejście z M(X)Do M(X 2) umożliwiło lepsze uwzględnienie wpływu na oczekiwanie matematyczne tej możliwej wartości, która jest duża i ma małe prawdopodobieństwo. Oczywiście, jeśli wartość X miał kilka dużych i mało prawdopodobnych wartości, następnie przejście do wartości X 2, a tym bardziej do ilości X 3 , X 4 itd., pozwoliłyby nam na dalsze „wzmocnienie roli” tych dużych, ale mało prawdopodobnych możliwych wartości. Dlatego celowe okazuje się uwzględnienie matematycznego oczekiwania całkowitej dodatniej potęgi zmiennej losowej (nie tylko dyskretnej, ale także ciągłej).
Początkowy moment zamówienia k zmienna losowa X nazywa się matematycznym oczekiwaniem wielkości Xk:
v k = M(X).
W szczególności,
w 1 = M(X), w 2 = M(X 2).
Korzystając z tych punktów, wzór na obliczenie wariancji D(X)= M(X 2)- [M(X)] 2 można zapisać w ten sposób:
D(X)= w 2 – . (*)
Oprócz momentów zmiennej losowej X wskazane jest uwzględnienie momentów odchylenia X-M(X).
Centralnym momentem rzędu k zmiennej losowej X jest matematyczne oczekiwanie wielkości(HM(X))k:
W szczególności,
Łatwo wyprowadzić zależności łączące moment początkowy i centralny. Na przykład porównując (*) i (***) otrzymujemy
m 2 = w 2 – .
Opierając się na definicji momentu centralnego i korzystając z własności oczekiwań matematycznych, nie jest trudno otrzymać wzory:
m 3 = w 3 – 3w 2 w 1 + 2 ,
m 4= w 4 – 4w 3 w 1 + 6w 2 + 3 .
Momenty wyższego rzędu są rzadko używane.
Komentarz. Omawiane tutaj punkty nazywane są teoretyczny. W przeciwieństwie do momentów teoretycznych, nazywane są momenty obliczone na podstawie danych obserwacyjnych empiryczny. Poniżej podano definicje momentów empirycznych (patrz rozdział XVII, § 2).
Zadania
1. Znane są wariancje dwóch niezależnych zmiennych losowych: D(X) = 4, D(Y)=3. Znajdź wariancję sumy tych wielkości.
Reprezentant. 7.
2. Wariancja zmiennej losowej X jest równe 5. Znajdź wariancję następujących wielkości: a) X-1; b) -2 X; V) ZH + 6.
Reprezentant. a) 5; b) 20; c) 45.
3. Losowa wartość X przyjmuje tylko dwie wartości: +C i -C, każda z prawdopodobieństwem 0,5. Znajdź wariancję tej wielkości.
Reprezentant. Z 2 .
4. , znając prawo jego dystrybucji
| X | 0, 1 | |||
| P | 0, 4 | 0, 2 | 0, 15 | 0, 25 |
Reprezentant. 67,6404.
5. Losowa wartość X może przyjmować dwie możliwe wartości: X 1 z prawdopodobieństwem 0,3 i X 2 z prawdopodobieństwem 0,7 i X 2 > x 1 . Znajdować X 1 i X 2, wiedząc o tym M(X) = 2, 7i D(X) =0,21.
Reprezentant. X 1 = 2, X 2 = 3.
6. Znajdź wariancję zmiennej losowej X-liczba wystąpień zdarzeń A We dwóch niezależne testy, Jeśli M(X) = 0, 8.
Notatka. Napisz dwumianowe prawo rozkładu prawdopodobieństwa liczby wystąpień zdarzenia A w dwóch niezależnych badaniach.
Reprezentant. 0, 48.
7. Testowane jest urządzenie składające się z czterech niezależnie działających urządzeń. Prawdopodobieństwo awarii urządzenia jest następujące: R 1 = 0,3; R 2 = 0,4; P 3 = 0,5; R 4 = 0,6. Znajdź matematyczne oczekiwanie i wariancję liczby uszkodzonych urządzeń.
Reprezentant. 1,8; 0,94.
8. Znajdź wariancję zmiennej losowej X- liczba wystąpień zdarzenia w 100 niezależnych próbach, w każdej z których prawdopodobieństwo wystąpienia zdarzenia wynosi 0,7.
Reprezentant. 21.
9. Wariancja zmiennej losowej D(X) = 6,25. Znajdź odchylenie standardowe s( X).
Reprezentant. 2, 5.
10. Zmienna losowa jest określona przez prawo dystrybucji
| X | |||
| P | 0, 1 | 0, 5 | 0, 4 |
Znajdź odchylenie standardowe tej wartości.
Reprezentant. 2, 2.
11. Wariancja każdej z 9 wzajemnie niezależnych zmiennych losowych o jednakowym rozkładzie jest równa 36. Znajdź wariancję średniej arytmetycznej tych zmiennych.
Reprezentant. 4.
12. Odchylenie standardowe każdej z 16 wzajemnie niezależnych zmiennych losowych o jednakowym rozkładzie wynosi 10. Znajdź odchylenie standardowe średniej arytmetycznej tych zmiennych.
Reprezentant. 2,5.
Rozdział dziewiąty
PRAWO DUŻYCH LICZB
Uwagi wstępne
Jak już wiadomo, nie można z całą pewnością przewidzieć z góry, które z możliwych wartości przyjmie zmienna losowa w wyniku testu; to zależy od wielu przyczyny przypadkowe, których nie można brać pod uwagę. Wydawać by się mogło, że skoro w tym sensie dysponujemy bardzo skromnymi informacjami o każdej zmiennej losowej, ustalenie wzorców zachowań i sumy dostatecznie dużej liczby zmiennych losowych jest prawie niemożliwe. W rzeczywistości nie jest to prawdą. Okazuje się, że dla niektórych stosunkowo szerokie warunki ogólne zachowanie wystarczająco dużej liczby zmiennych losowych prawie traci swój losowy charakter i staje się naturalne.
W praktyce bardzo ważna jest znajomość warunków, w jakich połączone działanie wielu przyczyn losowych prowadzi do skutku niemal niezależnego od przypadku, gdyż pozwala przewidzieć przebieg zjawisk. Warunki te są wskazane w twierdzeniach Nazwa zwyczajowa prawo duże liczby. Należą do nich twierdzenia Czebyszewa i Bernoulliego (istnieją inne twierdzenia, które nie są tutaj omawiane). Twierdzenie Czebyszewa jest najbardziej ogólnym prawem wielkich liczb, twierdzenie Bernoulliego jest najprostsze. Aby udowodnić te twierdzenia, skorzystamy z nierówności Czebyszewa.
Nierówność Czebyszewa
Nierówność Czebyszewa obowiązuje dla dyskretnych i ciągłych zmiennych losowych. Dla uproszczenia ograniczymy się do udowodnienia tej nierówności dla wielkości dyskretnych.
Rozważmy dyskretną zmienną losową X, określone przez tabelę rozkładu:
| X | X 1 | X 2 | … | x rz |
| P | P 1 | P 2 | … | p.n |
Postawmy sobie zadanie oszacowania prawdopodobieństwa, że odchylenie zmiennej losowej od jej oczekiwań matematycznych nie przekroczy wartości bezwzględnej liczby dodatniej e. Jeśli e jest wystarczająco małe, oszacowamy prawdopodobieństwo, że X przyjmie wartości dość zbliżone do swoich matematycznych oczekiwań. P. L. Czebyszew udowodnił nierówność, która pozwala podać interesujące nas oszacowanie.
Nierówność Czebyszewa. Prawdopodobieństwo, że odchylenie zmiennej losowej X od jej matematycznych oczekiwań w wartości bezwzględnej jest mniejsze niż liczba dodatnia e, jest nie mniejsze niż 1-D(X)/mi 2 :
R(|X-M(X)|< e ) 1-D(X)/mi 2 .
Dowód. Od zdarzeń polegających na realizacji nierówności |X-M(X)|
R(|X-M(X)|< e )+ R(|X-M(X)| mi)= 1.
Stąd prawdopodobieństwo, które nas interesuje
R(|X-M(X)|< e )= 1- R(|X-M(X)| mi). (*)
Zatem problem sprowadza się do obliczenia prawdopodobieństwa R(| HM(X)| mi).
Zapiszmy wyrażenie na wariancję zmiennej losowej X:
D(X)= [X 1 -M(X)] 2 P 1 + [X 2 -M(X)] 2 P 2 +…+ [x n-M(X)]2przyp.
Oczywiście wszystkie wyrazy tej sumy są nieujemne.
Odrzućmy te terminy, dla których | x ja-M(X)|<mi(dla pozostałych terminów | x j-M(X)| mi), W rezultacie kwota może się jedynie zmniejszyć. Załóżmy dla pewności, że k pierwsze wyrazy (bez utraty ogólności możemy założyć, że w tabeli rozkładu możliwe wartości są ponumerowane dokładnie w tej kolejności). Zatem,
D(X) [x k + 1 -M(X)] 2 p k + 1 + [x k + 2 -M(X)] 2 p k + z + ... +[x n-M(X)] 2 przyp.
Zauważ, że obie strony nierówności | x j - M(X)| mi (J = k+1, k+ 2, ..., P) są dodatnie, zatem podnosząc je do kwadratu otrzymujemy równoważną nierówność | x j - M(X)| 2 mi 2 Skorzystajmy z tej uwagi i zastępując każdy z czynników w pozostałej sumie | x j - M(X)| 2 w liczbie mi 2(w tym przypadku nierówność może tylko wzrosnąć), otrzymujemy
D(X) mi 2 (r k+ 1 + p k + 2 + … + р n). (**)
Zgodnie z twierdzeniem o dodawaniu, suma prawdopodobieństw r k+ 1 + p k + 2 + … + р n istnieje taka możliwość X przyjmie jedną, nieważne która z wartości x k + 1 , xk+ 2 ,....xp, i dla każdego z nich odchylenie spełnia nierówność | x j - M(X)| mi Wynika z tego, że kwota r k+ 1 + p k + 2 + … + р n wyraża prawdopodobieństwo
P(|X - M(X)| mi).
Powyższe rozważania pozwalają nam przepisać nierówność (**) w następujący sposób:
D(X) e 2 P(|X - M(X)| mi),
P(|X - M(X)| mi)D(X) /mi 2 (***)
Podstawiając (***) do (*), w końcu otrzymujemy
P(|X - M(X)| <mi) 1- D(X) /mi 2 ,
co było do okazania
Komentarz. Nierówność Czebyszewa ma ograniczone znaczenie praktyczne, ponieważ często daje przybliżone, a czasem trywialne (nieinteresujące) oszacowanie. Na przykład, jeśli D(X)>tj 2 i dlatego D(X)/mi 2 > 1, potem 1 - D(X)/mi 2 < 0; Zatem w tym przypadku nierówność Czebyszewa wskazuje jedynie, że prawdopodobieństwo odchylenia jest nieujemne, co jest już oczywiste, ponieważ każde prawdopodobieństwo wyraża się liczbą nieujemną.
Teoretyczne znaczenie nierówności Czebyszewa jest bardzo duże. Poniżej wykorzystamy tę nierówność do wyprowadzenia twierdzenia Czebyszewa.
Twierdzenie Czebyszewa
Twierdzenie Czebyszewa. Jeśli X 1 , X 2 ,…, X n, ...-parami niezależne zmienne losowe, a ich wariancje są równomiernie ograniczone(nie przekraczać stałej liczby C), to niezależnie od tego, jak mała jest liczba dodatnia e, prawdopodobieństwo nierówności
Innymi słowy, zgodnie z warunkami twierdzenia
Zatem twierdzenie Czebyszewa stwierdza, że jeśli weźmie się pod uwagę wystarczająco dużą liczbę niezależnych zmiennych losowych o ograniczonych wariancjach, to zdarzenie można uznać za prawie wiarygodne, polegające na tym, że odchylenie średniej arytmetycznej zmiennych losowych od średniej arytmetycznej ich oczekiwania matematyczne będą dowolnie duże, a wartość bezwzględna mała
Dowód. Wprowadźmy do rozważań nową zmienną losową – średnią arytmetyczną zmiennych losowych
=(X 1 +X 2 +…+X rz)/N.
Znajdźmy oczekiwanie matematyczne . Korzystając z właściwości oczekiwania matematycznego (ze znaku oczekiwania matematycznego można wyjąć stały współczynnik, oczekiwanie matematyczne sumy jest równe sumie oczekiwań matematycznych wyrazów) otrzymujemy
M ![]() =
=
![]() . (*)
. (*)
Stosując nierówność Czebyszewa do ilości, mamy
Podstawiając prawą stronę (***) do nierówności (**) (dlatego tę drugą można jedynie wzmocnić), mamy
Stąd, przechodząc do granicy w , otrzymujemy
Wreszcie, biorąc pod uwagę, że prawdopodobieństwo nie może przekraczać jedności, możemy w końcu napisać
Twierdzenie zostało udowodnione.
Powyżej, formułując twierdzenie Czebyszewa, założyliśmy, że zmienne losowe mają różne oczekiwania matematyczne. W praktyce często zdarza się, że zmienne losowe mają takie same oczekiwania matematyczne. Oczywiście, jeśli ponownie założymy, że rozproszenia tych wielkości są ograniczone, wówczas będzie miało do nich zastosowanie twierdzenie Czebyszewa.
Oznaczmy matematyczne oczekiwanie każdej ze zmiennych losowych przez A; w rozpatrywanym przypadku średnia arytmetyczna oczekiwań matematycznych, jak łatwo zauważyć, jest również równa A. Dla konkretnego rozpatrywanego przypadku możemy sformułować twierdzenie Czebyszewa.
Jeśli X 1 , X 2 , ..., KM...-parami niezależne zmienne losowe, które mają takie same oczekiwania matematyczne a, a jeśli wariancje tych zmiennych są równomiernie ograniczone, to niezależnie od tego, jak mała jest liczba e>Och, prawdopodobieństwo nierówności
![]()
będzie tak blisko jedności, jak to pożądane, jeśli liczba zmiennych losowych jest wystarczająco duża.
Innymi słowy, zgodnie z warunkami twierdzenia będzie równość

Istota twierdzenia Czebyszewa
Istota sprawdzonego twierdzenia jest następująca: choć poszczególne niezależne zmienne losowe mogą przyjmować wartości odbiegające od ich matematycznych oczekiwań, to średnia arytmetyczna dostatecznie dużej liczby zmiennych losowych z dużym prawdopodobieństwem przyjmuje wartości bliskie pewnej stałej liczba, a mianowicie liczba ( M(X 1)+ M(X 2)+...+M(X s))/P(lub pod numer A w specjalnym przypadku). Innymi słowy, poszczególne zmienne losowe mogą wykazywać znaczny rozrzut, a ich średnia arytmetyczna jest rozproszonie mała.
Zatem nie można z całą pewnością przewidzieć, jaką możliwą wartość przyjmie każda ze zmiennych losowych, ale można przewidzieć, jaką wartość przyjmie ich średnia arytmetyczna.
Więc, średnia arytmetyczna wystarczająco dużej liczby niezależnych zmiennych losowych(którego wariancje są równomiernie ograniczone) traci charakter zmiennej losowej. Wyjaśnia to fakt, że odchylenia każdej z wielkości od ich oczekiwań matematycznych mogą być zarówno dodatnie, jak i ujemne, a w średniej arytmetycznej znoszą się.
Twierdzenie Czebyszewa obowiązuje nie tylko dla dyskretnych, ale także dla ciągłych zmiennych losowych; tak się składa, że ona jest świecący przykład, potwierdzając słuszność doktryny materializmu dialektycznego o związku przypadku z koniecznością.
Wartość oczekiwana. Oczekiwanie matematyczne Dyskretna zmienna losowa X, przyjmując skończoną liczbę wartości XI z prawdopodobieństwami RI, kwota ta nazywa się:
Oczekiwanie matematyczne ciągła zmienna losowa X nazywa się całką iloczynu jej wartości X na gęstość rozkładu prawdopodobieństwa F(X):
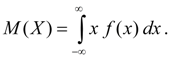 (6B)
(6B)
Całka niewłaściwa (6 B) przyjmuje się, że jest absolutnie zbieżny (w przeciwnym razie mówią, że jest to oczekiwanie matematyczne M(X) nie istnieje). Charakteryzuje się oczekiwaniem matematycznym Średnia wartość zmienna losowa X. Jego wymiar pokrywa się z wymiarem zmiennej losowej.
Właściwości oczekiwań matematycznych:
Dyspersja. Zmienność zmienna losowa X numer nazywa się:
Różnica jest charakterystyka rozpraszania losowe wartości zmiennych X w stosunku do jego średniej wartości M(X). Wymiar wariancji jest równy kwadratowi wymiaru zmiennej losowej. Bazując na definicjach wariancji (8) i oczekiwaniu matematycznym (5) dla dyskretnej zmiennej losowej i (6) dla ciągłej zmiennej losowej otrzymujemy podobne wyrażenia na wariancję:
 (9)
(9)
Tutaj M = M(X).
Właściwości dyspersji:
Odchylenie standardowe:
![]() (11)
(11)
Ponieważ wymiar średniej odchylenie kwadratowe podobnie jak zmienna losowa, częściej jest używana jako miara rozproszenia niż wariancji.
Momenty dystrybucji. Pojęcia matematycznego oczekiwania i rozproszenia są szczególnymi przypadkami więcej ogólna koncepcja dla numerycznych charakterystyk zmiennych losowych – momenty dystrybucji. Momenty rozkładu zmiennej losowej wprowadza się jako oczekiwania matematyczne prostych funkcji zmiennej losowej. A więc chwila porządku k w stosunku do punktu X Wartość 0 nazywa się oczekiwaniem matematycznym M(X–X 0 )k. Chwile o pochodzeniu X= 0 są wywoływane początkowe chwile i są oznaczone:
![]() (12)
(12)
Momentem początkowym pierwszego rzędu jest środek rozkładu rozpatrywanej zmiennej losowej:
![]() (13)
(13)
Chwile o centrum dystrybucji X= M są nazywane punkty centralne i są oznaczone:
![]() (14)
(14)
Z (7) wynika, że moment centralny pierwszego rzędu jest zawsze równy zeru:
Momenty centralne nie zależą od pochodzenia wartości zmiennej losowej, ponieważ są przesunięte o stałą wartość Z jego środek dystrybucji przesuwa się o tę samą wartość Z, a odchylenie od środka nie zmienia się: X – M = (X – Z) – (M – Z).
Teraz to oczywiste dyspersja- Ten moment centralny drugiego rzędu:
Asymetria. Moment centralny trzeciego rzędu:
![]() (17)
(17)
służy ocenie asymetrie dystrybucji. Jeśli rozkład jest symetryczny względem punktu X= M, wówczas moment centralny trzeciego rzędu będzie równy zeru (jak wszystkie momenty centralne rzędów nieparzystych). Dlatego też, jeżeli moment centralny trzeciego rzędu jest różny od zera, to rozkład nie może być symetryczny. Wielkość asymetrii ocenia się za pomocą bezwymiarowości współczynnik asymetrii:
 (18)
(18)
Znak współczynnika asymetrii (18) wskazuje na asymetrię prawostronną lub lewostronną (rys. 2).

Ryż. 2. Rodzaje asymetrii rozkładu.
Nadmiar. Moment centralny czwartego rzędu:
![]() (19)
(19)
służy do oceny tzw nadmiar, który określa stopień stromości (szczytu) krzywej rozkładu w pobliżu środka rozkładu w stosunku do krzywej rozkładu normalnego. Ponieważ dla rozkładu normalnego wartość przyjęta jako kurtoza wynosi:
 (20)
(20)
Na ryc. Rysunek 3 pokazuje przykłady krzywych rozkładu o różnych wartościach kurtozy. Do rozkładu normalnego mi= 0. Krzywe, które są bardziej szczytowe niż normalnie, mają kurtozę dodatnią, a te, które są bardziej płaskie, mają kurtozę ujemną.

Ryż. 3. Krzywe rozkładu z różnym stopniu chłód (nadmiar).
Momenty wyższego rzędu w zastosowaniach inżynierskich statystyka matematyczna zwykle nie używany.
Moda
oddzielny zmienna losowa to jej najbardziej prawdopodobna wartość. Moda ciągły zmienna losowa to jej wartość, przy której gęstość prawdopodobieństwa jest maksymalna (rys. 2). Jeżeli krzywa rozkładu ma jedno maksimum, wówczas nazywa się rozkład jednomodalny. Jeżeli krzywa rozkładu ma więcej niż jedno maksimum, wówczas nazywa się rozkład multimodalny. Czasami istnieją rozkłady, których krzywe mają raczej minimum niż maksimum. Takie rozkłady nazywane są antymodalne. W przypadek ogólny tryb i oczekiwanie matematyczne zmiennej losowej nie pokrywają się. W szczególnym przypadku, np modalny, tj. mający modę, rozkład symetryczny i pod warunkiem, że istnieje oczekiwanie matematyczne, to drugie pokrywa się z trybem i środkiem symetrii rozkładu.
Mediana zmienna losowa X– taki jest jego sens Meh, dla którego zachodzi równość: tj. jest równie prawdopodobne, że zmienna losowa X będzie mniej lub więcej Meh. Geometrycznie mediana jest odciętą punktu, w którym pole pod krzywą rozkładu jest podzielone na pół (ryc. 2). W przypadku symetrycznego rozkładu modalnego mediana, moda i oczekiwanie matematyczne są takie same.








