Определение. Нека функция f(x) е дефинирана на някакъв интервал и x 0 е точка в този интервал. Ако , тогава се казва, че f(x) е непрекъсната в точката x 0 .
От дефиницията следва, че можем да говорим за непрекъснатост само по отношение на онези точки, в които е дефинирана f(x) (при дефинирането на границата на функция такова условие не е било поставено). За непрекъснати функции , тоест операциите f и lim са комутируеми. Съответно на две дефиниции на границата на функция в точка могат да се дадат две дефиниции на непрекъснатост - „на езика на последователностите“ и „на езика на неравенствата“ (на езика на ε-δ). Препоръчително е да направите това сами.
За практическа употреба понякога е по-удобно непрекъснатостта да се дефинира на езика на нарастванията.
Стойността Δx=x-x 0 се нарича увеличение на аргумента, а Δy=f(x)-f(x 0) е увеличението на функцията при преместване от точка x 0 към точка x.
Определение. Нека f(x) е дефинирано в точка x 0 . Функция f(x) се нарича непрекъсната в точка x 0, ако безкрайно малко увеличение на аргумента в тази точка съответства на безкрайно малко увеличение на функцията, тоест Δy→0 за Δx→0.

Пример 1. Докажете, че функцията y=sinx е непрекъсната за всяка стойност на x.
Решение. Нека x 0 е произволна точка. Давайки му увеличение Δx, получаваме точката x=x 0 +Δx. Тогава . Получаваме .
Определение. Функцията y=f(x) се нарича непрекъсната в точката x 0 отдясно (вляво), ако
.
Функция, непрекъсната във вътрешна точка, ще бъде непрекъсната както вдясно, така и вляво. Обратното също е вярно: ако една функция е непрекъсната в точка отляво и отдясно, тогава тя ще бъде непрекъсната в тази точка. Една функция обаче може да бъде непрекъсната само от едната страна. Например за , , f(1)=1, следователно тази функция е непрекъсната само отляво (за графиката на тази функция вижте параграф 5.7.2 по-горе).
Определение. Една функция се нарича непрекъсната на някакъв интервал, ако е непрекъсната във всяка точка от този интервал.
По-специално, ако интервалът е сегмент, тогава в неговите краища се подразбира едностранна непрекъснатост.

Свойства на непрекъснатите функции

1. Всички елементарни функции са непрекъснати в своята област на дефиниция.
2. Ако f(x) и φ(x), дадени на определен интервал, са непрекъснати в точката x 0 на този интервал, тогава функциите също ще бъдат непрекъснати в тази точка.
3. Ако y=f(x) е непрекъснат в точката x 0 от X и z=φ(y) е непрекъснат в съответната точка y 0 =f(x 0) от Y, тогава сложна функция z=φ(f(x)) ще бъде непрекъснато в точка x 0 .

Функционални прекъсвания и тяхната класификация

Знак за непрекъснатост на функцията f(x) в точката x 0 е равенството, което предполага наличието на три условия:
1) f(x) е дефинирана в точка x 0 ;
2) ;
3) .
Ако поне едно от тези изисквания е нарушено, тогава x 0 се нарича точка на прекъсване на функцията. С други думи, точката на прекъсване е точка, в която тази функция не е непрекъсната. От определението за точки на прекъсване следва, че точките на прекъсване на функция са:
а) точки, принадлежащи към областта на дефиниране на функцията, при която f(x) губи свойството на непрекъснатост,
б) точки, които не принадлежат на областта на дефиниране на f(x), които са съседни точки на два интервала от областта на дефиниция на функцията.
Например за функция точката x=0 е точка на прекъсване, тъй като функцията в тази точка не е дефинирана и функцията има прекъсване в точката x=1, която е съседна на два интервала (-∞,1) и (1,∞) от областта на дефиниране на f(x) и не съществува.

Следната класификация е приета за точки на прекъсване.
1) Ако в точката x 0 има крайни И , но f(x 0 +0)≠f(x 0 -0), тогава x 0 се нарича точка на прекъсване от първи род , и се нарича скок на функцията .

Пример 2. Помислете за функцията
Функцията може да бъде разбита само в точката x=2 (в останалите точки тя е непрекъсната като всеки полином).
Ще намерим , . Тъй като едностранните граници са крайни, но не са равни една на друга, то в точката x=2 функцията има прекъсване от първи род. забележи това , следователно функцията в тази точка е непрекъсната вдясно (фиг. 2).
2) Точки на прекъсване от втори род се наричат ​​точки, в които поне една от едностранните граници е равна на ∞ или не съществува.

Пример 3. Функцията y=2 1/ x е непрекъсната за всички стойности на x с изключение на x=0. Нека намерим едностранни ограничения: , , следователно x=0 е точка на прекъсване от втори род (фиг. 3).
3) Точка x=x 0 се нарича подвижна точка на прекъсване , ако f(x 0 +0)=f(x 0 -0)≠f(x 0).
Ще „елиминираме“ празнината в смисъл, че е достатъчно да променим (предефинираме или предефинираме) стойността на функцията в тази точка, като зададем , и функцията ще стане непрекъсната в точката x 0 .
Пример 4. Известно е, че и тази граница не зависи от начина, по който x клони към нула. Но функцията в точка x=0 не е дефинирана. Ако предефинираме функцията, като зададем f(0)=1, тогава тя се оказва непрекъсната в тази точка (в други точки тя е непрекъсната като частно на непрекъснатите функции sinx и x).
Пример 5. Изследване на непрекъснатостта на функция .
Решение. Функциите y=x 3 и y=2x са определени и непрекъснати навсякъде, включително и в посочените интервали. Нека разгледаме точката на свързване на интервалите x=0:
, , . Получаваме, че , което означава, че в точката x=0 функцията е непрекъсната.
Определение. Функция, която е непрекъсната на интервал, с изключение на краен брой точки на прекъсване от първи вид или отстраним прекъсване, се нарича частично непрекъсната на този интервал.

Примери за прекъснати функции

Пример 1. Функцията е дефинирана и непрекъсната върху (-∞,+∞) с изключение на точката x=2. Да определим вида на прекъсването. Тъй като И , то в точката x=2 има прекъсване от втори род (фиг. 6).
Пример 2. Функцията е дефинирана и непрекъсната за всички x с изключение на x=0, където знаменателят е нула. Нека намерим едностранни граници в точката x=0:
Едностранните граници са крайни и различни, следователно x=0 е точка на прекъсване от първи род (фиг. 7).
Пример 3. Определете в кои точки и какъв вид прекъсвания има функцията
Тази функция е дефинирана на [-2,2]. Тъй като x 2 и 1/x са непрекъснати в интервалите [-2,0] и съответно, прекъсването може да възникне само на кръстовището на интервалите, тоест в точката x=0. Тъй като , тогава x=0 е точка на прекъсване от втори род.

Пример 4. Възможно ли е да се премахнат функционалните пропуски:
а) в точка х=2;
б) в точка х=2;
V) в точка х=1?
Решение. По отношение на пример а) можем веднага да кажем, че прекъсването f(x) в точката x=2 не може да бъде елиминирано, тъй като в тази точка има безкрайни едностранни граници (виж пример 1).
б) Функцията g(x) въпреки че има крайни едностранни граници в точката x=2

(,),

но те не съвпадат, така че празнината също не може да бъде премахната.
в) Функцията φ(x) в точката на прекъсване x=1 има равни едностранни крайни граници: . Следователно празнината може да бъде елиминирана чрез предефиниране на функцията при x=1 чрез поставяне на f(1)=1 вместо f(1)=2.

Пример 5. Покажете, че функцията на Дирихле

прекъснат във всяка точка на числовата ос.
Решение. Нека x 0 е всяка точка от (-∞,+∞). Във всеки от неговите квартали има както рационални, така и ирационални точки. Това означава, че във всеки квартал на x 0 функцията ще има стойности, равни на 0 и 1. В този случай не може да има граница на функцията в точката x 0 нито отляво, нито отдясно, което означава че функцията на Дирихле има прекъсвания от втори род във всяка точка на реалната ос.

Пример 6. Намерете точки на прекъсване на функцията

и определя техния вид.
Решение. Точките, за които се подозира, че са счупени, са точки x 1 =2, x 2 =5, x 3 =3.
В точката x 1 =2 f(x) има прекъсване от втори род, тъй като
.
Точката x 2 =5 е точка на непрекъснатост, тъй като стойността на функцията в тази точка и в нейната близост се определя от втория ред, а не от първия: .
Нека разгледаме точката x 3 =3: , , от което следва, че x=3 е точка на прекъсване от първи род.

За независимо решение.
Разгледайте функциите за непрекъснатост и определете типа точки на прекъсване:
1) ; Отговор: x=-1 – точка на отстраним прекъсване;
2) ; Отговор: Прекъснатост от втори род в точка x=8;
3) ; Отговор: Прекъснатост от първи род при x=1;
4)
Отговор: В точката x 1 =-5 има отстранима празнина, в x 2 =1 има празнина от втори род и в точката x 3 =0 има празнина от първи вид.
5) Как трябва да се избере числото A, така че функцията

ще бъде непрекъснато при x=0?
Отговор: A=2.
6) Възможно ли е да се избере числото A, така че функцията

ще бъде непрекъснато при x=2?
Отговор: не.

Непрекъснатост на функция в точка. Функция y = f(x ) се нарича непре-

рязко в точка x 0, ако:

1) тази функция е дефинирана в някаква околност на точката x 0;

2) има лимит f(x);

→ x 0

3) тази граница равно на стойносттафункции в точка x 0, т.е. limf (x )= f (x 0 ) .
		x→x0
Последното условие е еквивалентно на условието lim		y = 0, където x = x − x 0 – когато
	x→ 0
завъртане на аргумента, y = f (x 0 +	x )− f (x 0 ) – нарастване на функцията, съотв
увеличаване на аргумента	х, т.е. функция	f(x) е непрекъснато при x 0

ако и само ако в този момент безкрайно малко увеличение на аргумента съответства на безкрайно малко увеличение на функцията.

Еднопосочна непрекъснатост.Функцията y = f (x) се нарича непрекъсната

отляво в точката x 0, ако е дефинирана на някакъв полуинтервал (a ;x 0 ]

и lim f (x)= f (x 0).

x→ x0 − 0

За функция y = f (x) се казва, че е непрекъсната отдясно в точката x 0, ако е оп-

се разпределя в определен полуинтервал [ x 0 ;a ) и limf (x )= f (x 0 ) .

x→ x0 + 0

Функция y = f(x)		непрекъснато в точка x 0			тогава и само когато тя
непрекъснато
lim f (x)= limf (x)= limf (x)= f (x 0).
x→ x0 + 0	x→ x0 − 0	x→x0

Непрекъснатост на функция върху множество. Извиква се функцията y = f (x).

непрекъснато на снимачната площадка X, ако е непрекъсната във всяка точка от това множество. Освен това, ако дадена функция е дефинирана в края на определен интервал от числовата ос, тогава непрекъснатостта в тази точка се разбира като непрекъснатост отдясно или отляво. По-специално, функцията y = f (x) се нарича не-

прекъснат на сегмента [a; b] ако тя

1) непрекъснато във всяка точка от интервала(a;b) ;

2) е дясно непрекъснато в точкаа;

3) остава непрекъснато в точка b.

Точки на прекъсване на функцията.Точката x 0, принадлежаща към областта на дефиниране на функцията y = f (x) или гранична точка на тази област, се нарича

точка на прекъсване на тази функция, ако (x) не е непрекъснат в тази точка.

Точките на прекъсване се разделят на точки на прекъсване от първи и втори вид:

1) Ако има крайни граници lim f (x )= f (x 0 − 0) и

x→ x0 − 0

	f (x)= f (x 0 + 0) и не всичките три числа са f (x 0 − 0), f (x 0 + 0),		f (x 0 ) са равни
x→ x0 + 0
помежду си, след това x 0		се нарича точка на прекъсване от първи род.
	По-специално, ако лявата и дясната граница на функцията в точката x 0		равен между
	себе си, но	не са равни на стойността на функцията в този момент:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , тогава x 0 се нарича отстранима точка на прекъсване.

В този случай, като зададете f (x 0 )= A, можете да промените функцията в точка x 0

така че да стане непрекъснат ( предефинирайте функцията чрез непрекъснатост). Разликата f (x 0 + 0)− f (x 0 − 0) се нарича скок на функция в точка x 0 .

Скокът на функцията в точката на отстраним прекъсване е нула.

2) Наричат ​​се точки на прекъсване, които не са точки на прекъсване от първи род точки на прекъсване от втори вид. В точките на прекъсване от втори вид поне една от едностранните граници f (x 0 − 0) и f (x 0 + 0) не съществува или е безкрайна.

Свойства на функции, непрекъснати в точка.

		f(x)	и g (x) са непрекъснати в точката x 0, тогава функциите
f(x)±g(x),	f(x)g(x) и	f(x)	(където g (x)≠ 0) също са непрекъснати в точка x.
		g(x)

2) Ако функцията u (x) е непрекъсната в точката x 0, а функцията f (u) е непрекъсната

в точката u 0 = u (x 0), тогава комплексната функция f (u (x)) е непрекъсната в точката x 0.

3) Всички основни елементарни функции (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) са непрекъснати във всяка

до точката на техните области на дефиниране.

От свойства 1)–3) следва, че всички елементарни функции (функции, получени от основни елементарни функции с помощта на краен брой аритметични операции и операции на съставяне) също са непрекъснати във всяка точка от своите области на дефиниране.

Свойства на функции, непрекъснати на интервал.

1) (теорема за междинна стойност) Нека функцията f(x) е дефинирана

върху и е непрекъснат на отсечката [a;b]. Тогава за произволно число C от ограденото

между числата f (a) и f (b), (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Теорема на Болцано-Коши

е прекъснат на отсечката [a;b] и приема стойности на различни знаци в краищата си.

Тогава има поне една точка x 0 [ a ; b ], така че f (x 0 )= 0 .

3) (1-во Теорема на Вайерщрас) Нека функцията f (x) е дефинирана и

разкъсан на сегмента [a;b]. Тогава тази функция е ограничена в този сегмент.

4) (2-ро Теорема на Вайерщрас) Нека функцията f (x) е дефинирана и

бързаме на сегмента		[a;b] . Тогава тази функция достига на интервала [ a ; b ]
най-великия		най-малко	ценности, т.е.	съществуват
x1, x2 [a; б],		за всякакви	точки x [a;b]	справедлив	неравенства

f (x 1 ) ≤ f (x ) ≤ f (x 2 ) .

Пример 5.17. Използвайки определението за непрекъснатост, докажете, че функцията y = 3x 2 + 2x − 5 е непрекъсната в произволна точка x 0 на числовата ос.

Решение: Метод 1: Нека x 0 е произволна точка на числовата ос. Вие-

Първо изчисляваме границата на функцията f (x) като x → x 0, прилагайки теоремите за границата на сумата и произведението на функциите:

lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2							− 5.
x→x0	x→x0	x→x0	x→x0
След това изчисляваме стойността на функцията в точка x:f (x)= 3x 2							− 5 .
Сравнявайки получените резултати, виждаме				lim f (x)= f (x 0) което според
				x→x0

определение и означава непрекъснатостта на разглежданата функция в точката x 0.

Метод 2: Нека		x – нарастване на аргумента в точка x 0. Да намерим кореспонденцията
подходящо	нарастване			y = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
Нека сега изчислим границата на увеличението на функцията, когато нарастването на аргумента
		се стреми

	y = lim (6x + 2)		x + (x )2 = (6x + 2) lim		x + (limx)2 = 0.
x→ 0	x→ 0			x→ 0	x→ 0

Така lim y = 0, което по дефиниция означава непрекъснатост

x→ 0

функции за всеки x 0 R .

Пример 5.18. Намерете точките на прекъсване на функцията f (x) и определете техния тип. IN

В случай на отстранимо прекъсване, дефинирайте функцията чрез непрекъснатост:

1) f (x) = 1− x 2 при x< 3;

5x, когато x ≥ 3

2) f (x)= x 2 + 4 x + 3;

х+1

	f(x)=
		x4 (x− 2)
	f(x)= арктан
			(x − 5)

Решение: 1) Домейнът на дефиниция на тази функция е цялото число

оста y (−∞ ;+∞ ) . На интервалите (−∞ ;3) ,(3;+∞ ) функцията е непрекъсната. Прекъсване е възможно само в точката x = 3, в която се променя аналитичната спецификация на функцията.

Нека намерим едностранните граници на функцията в посочената точка:

f (3− 0)= lim (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= lim 5x = 15.

x →3 +0

Виждаме, че лявата и дясната граница са крайни, така че x = 3
разкъсване I			f(x). Функция за прескачане към
f (3+ 0)− f (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , следователно в точката		х = 3

f(x) е непрекъсната отдясно.

2) Функцията е непрекъсната на цялата числова ос с изключение на точката x = − 1, в който не е дефиниран. Нека трансформираме израза за f (x), разширявайки числителя

дроби на множители:		f(x)=			4 х +3			(x + 1) (x + 3)	X + 3 за x ≠ − 1.
					х+1			х+1
Нека намерим едностранните граници на функцията в точката x = − 1:
	f(x)=лим	f (x )= lim(x + 3)= 2 .
x → −1−0	x → −1 +0		x → −1

Открихме, че лявата и дясната граница на функцията в изследваната точка съществуват, крайни са и равни една на друга, следователно x = − 1 е отстранима точка

права линия y = x + 3 с „надупчена“ точка M (− 1;2) . За да стане постоянна функцията

прекъснат, трябва да поставим f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

Така, след като допълнително дефинирахме f (x) чрез непрекъснатост в точката x = − 1, получихме функцията f * (x)= x + 3 с област на дефиниция (−∞ ;+∞) .

3) Тази функцияопределени и непрекъснати за всички x с изключение на точки

x = 0,x = 2, при което знаменателят на дробта става нула.

Разгледайте точката x = 0:

Тъй като в достатъчно малка околност на нула функцията отнема само

	за отрицателни стойности, тогава f (− 0)= lim			= −∞ = f (+0)	Тези. точка
			(x − 2)
	x → −0
	x = 0 е точка на прекъсване на втория вид функция		f(x).

Помислете сега за точката x = 2:

Функцията приема отрицателни стойности близо до лявата страна на разглежданата

	точка и положителните са отдясно, следователно				f (2− 0)=			= −∞,
							x4 (x− 2)
						x →2 −0
	f (2+ 0)= lim			= +∞ . Както в предишния случай, в точка x = 2
			(x − 2)
	x →2 +0

ция няма нито леви, нито десни крайни граници, т.е. страда от тип II разкъсване в този момент.

x = 5.

f (5− 0)= lim arctan

π ,f (5+ 0)= lim arctan

х = 5

(x − 5)

(x − 5)

x →5 −0

x →5 +0

ка разкъсване

f (5+ 0)− f (5− 0)=

π − (−

π )= π (виж Фиг. 5.2).

Проблеми за самостоятелно решаване

5,174. Използвайки само определението, докажете непрекъснатостта на функцията f (x) в

всяка точка x 0 R :

а) f(x) = c= const;		b) f (x)= x;
в) f (x)= x 3;		г) f (x)= 5x 2 − 4x + 1;
д) f (x) = sinx.
5,175. Докажете, че функцията	f(x) = x2	1, когато x ≥ 0,	е непрекъснато включен
		1 на х< 0
цялата числова линия. Постройте графика на тази функция.
5,176. Докажете, че функцията	f(x) = x2	1, когато x ≥ 0,	не е непрекъснат
		0 при х< 0

в точката x = 0, но е непрекъсната отдясно в тази точка. Начертайте графика на функцията f(x).

рязко в точка x =

Но е непрекъснат отляво в тази точка. Постройте графика

функции f(x).

5,178. Графични функции

а) y =

х+1

б) y= x+

х+1

х+1

х+1

Кои от условията за непрекъснатост в точките на прекъсване на тези функции са изпълнени и кои не са изпълнени?

5,179. Посочете точката на прекъсване на функцията

грях х		За x ≠ 0
		при x = 0

Кои от условията за непрекъснатост са изпълнени в този момент и кои не са изпълнени?

Определение точки на прекъсване на функцията и техните видове е продължение на темата за непрекъснатостта на функцията. Визуално (графично) обяснение на значението на точките на прекъсване на функция също е дадено в контраст с концепцията за непрекъснатост. Нека научим как да намираме точки на прекъсване на функция и да определяме техните типове. И нашите ще ни помогнат в това верни приятели- леви и десни граници, обикновено наричани едностранни граници. Ако някой има страх от едностранни ограничения, скоро ще го разсеем.

Точките на графиката, които не са свързани помежду си, се наричат точки на прекъсване на функцията . Графиката на такава функция, която претърпява прекъсване в точката x=2 - - на фигурата по-долу.

Обобщение на горното е следното определение. Ако функцията не е непрекъсната в точка, тогава тя има прекъсване в тази точка и самата точка се извиква точка на пречупване . Смущенията са от първи вид и от втори вид .

За да се определи видове (характер) на точките на прекъсване функциите трябва да бъдат намерени с увереност граници, така че е добра идея да отворите съответния урок в нов прозорец. Но във връзка с точките на прекъсване имаме нещо ново и важно - едностранни (ляво и дясно) ограничения. Най-общо те са написани (дясна граница) и (лява граница). Както в случая с границата по принцип, за да намерите границата на функция, трябва да замените X в израза на функцията за това, към което X клони. Но може би ще попитате как ще се различават дясната и лявата граница, ако в случая на дясната нещо се добави към X, но това нещо е нула, а в случая на лявата нещо се извади от X, но това нещо - също нула? И ще бъдеш прав. В повечето случаи.

Но в практиката на търсене на точки на прекъсване на функция и определяне на техния тип има два типични случая, когато дясната и лявата граница не са равни:

• функция има два или повече израза в зависимост от частта от числовата линия, към която x принадлежи (тези изрази обикновено се записват във къдрави скоби след f(х)= );
• в резултат на заместване на това, към което X клони, получаваме дроб, в чийто знаменател остава или плюс нула (+0), или минус нула (-0) и следователно такава дроб означава или плюс безкрайност, или минус безкрайност, и това са съвсем различни неща.

Точки на прекъсване от първи род

Точка на прекъсване от първи вид: функция има както крайна (т.е. не равна на безкрайност) лява граница, така и крайна дясна граница, но функцията не е дефинирана в точка или лявата и дясната граница са различни (не са равни).

Точка на отстранимо прекъсване от първи вид.Лявата и дясната граница са равни. В този случай е възможно допълнително да се дефинира функцията в точка. Да се ​​дефинира функция в точка, най-просто казано, означава да се осигури връзка от точки, между които има точка, в която лявата и дясната граница са равни една на друга. В този случай връзката трябва да представлява само една точка, в която трябва да се намери стойността на функцията.

Пример 1.Определете точката на прекъсване на функцията и вида (характера) на точката на прекъсване.

Точки на прекъсване от втори род

Точка на прекъсване от втори вид: точката, в която поне една от границите (лява или дясна) е безкрайна (равна на безкрайност).

Пример 3.

Решение. От израза за мощността при дясно е, че функцията не е дефинирана в точката. Нека намерим лявата и дясната граница на функцията в този момент:

Една от границите е равна на безкрайност, така че точката е точка на прекъсване от втори род. Графиката на функция с точка на прекъсване е под примера.

Намирането на точки на прекъсване на функция може да бъде или независима задача, или част от Пълно функционално изследване и графично изготвяне .

Пример 4.Определете точката на прекъсване на функцията и типа (характера) на точката на прекъсване за функцията

Решение. От израза за степен при 2 става ясно, че функцията не е дефинирана в точката. Нека намерим лявата и дясната граница на функцията в тази точка.

Подвижна празнина.

Определение. Точка анаречена отстранима точка на прекъсване на функцията y=f(x), ако границата на функцията f(x)съществува в тази точка, но в точката афункция f(x)или не е дефиниран, или има лично значение е(а), различен от лимита f(x)в този момент.

Пример. Например функцията

има в точката х=0ремонтируема празнина. Всъщност граничната стойност на тази функция в точката х=0е равно на 1. Частичната стойност е равна на 2.

Ако функцията f(x)има в точката аподвижна празнина, тогава тази празнина може да бъде елиминирана, без да се променят стойностите на функцията в точки, различни от а. За да направите това, достатъчно е да поставите стойността на функцията в точката аравна на граничната си стойност в тази точка. Така че в разгледания по-горе пример е достатъчно да поставите f(0)=1и тогава , т.е. функция f(x)ще стане непрекъснат в точката х=0.

Разстройство от първи вид.

Определение. Точка асе нарича точка на прекъсване от първи вид, ако в тази точка функцията f(x)има ограничени, но неравни десни и леви граници

Нека дадем няколко примера.

Пример. функция y=sgn xима в точката х=0разкъсване от първи вид. Всъщност и по този начин тези граници не са равни една на друга.

Пример. функция , дефинирани навсякъде с изключение на точката х=1, има в точката х=1разкъсване от първи вид. Наистина, .

Разстройство от втори вид.

Определение. Точка асе нарича точка на прекъсване от втори род, ако в тази точка функцията f(x)няма поне една от едностранните граници или ако поне една от едностранните граници е безкрайна.

Пример. функция f(x)=tan x, очевидно, има прекъсване от втори род във всяка точка x k =π/2+π k, k=0, ± 1, ± 2,..., защото във всяка такава точка

Пример. Функцията има прекъсване от втори род в точката х=0, тъй като в този момент тя няма нито дясна, нито лява граница.

Непрекъснатост на функция върху отсечка

Определение. Функция, дефинирана на интервал и непрекъсната във всяка негова точка се нарича непрекъсната на този сегмент.

Освен това, при непрекъснатост в точката асе разбира като непрекъснатост отдясно и като непрекъснатост в точка b- непрекъснатост отляво.

Ще кажем, че функцията y=f(x), определени на множеството (х)достига горния (долния) си ръб върху него , ако такава точка съществува x 0 ∈(x), Какво f(x 0)=β (f(x 0)=α).

[Вайерщрас] Теорема. Всяка функция, непрекъсната на интервал, е ограничена и достига своята горна граница и долната си граница върху него.

Теорема [Болцано-Коши]. Ако функцията y=f(x)непрекъснат на сегмента И f(a)=A, f(b)=B, след това за всякакви ° С, сключен между АИ б, има такъв момент ξ∈ , Какво f(ξ)=C.

С други думи, функция, непрекъсната на интервал, приемаща произволни две стойности, също приема всяка стойност, разположена между тях.

Последица. Ако една функция е непрекъсната на сегмент и приема стойности с различни знаци в своите краища, тогава има поне една точка на този сегмент, в която функцията изчезва.

Последица. Нека функцията y=f(x)непрекъснат на сегмента И , . След това функцията f(x)взема всички стойности от сегмента и само тези стойности.

По този начин наборът от всички стойности на функция, която е дадена и непрекъсната на определен сегмент, също е сегмент.

Непрекъснатост на функцията. Преломни точки.

Бикът върви, люлее се, въздиша като върви:
- Ох, дъската свършва, сега ще падна!

В този урок ще разгледаме концепцията за непрекъснатост на функция, класификацията на точките на прекъсване и общ практически проблем изследвания на непрекъснатостта на функциите. От самото име на темата мнозина интуитивно предполагат какво ще се обсъжда и смятат, че материалът е доста прост. Това е вярно. Но простите задачи най-често се наказват за пренебрегване и повърхностен подход към решаването им. Затова ви препоръчвам да проучите статията много внимателно и да уловите всички тънкости и техники.

Какво трябва да знаете и да можете?Не много. За да научите добре урока, трябва да разберете какво представлява той граница на функция. Читателите с ниско нивоподготовката е достатъчна, за да разберете статията Функционални ограничения. Примери за решенияи да гледам геометричен смисълограничение в ръководството Графики и свойства на елементарни функции. Също така е препоръчително да се запознаете с геометрични трансформации на графики, тъй като практиката в повечето случаи включва конструиране на чертеж. Перспективите са оптимистични за всички и дори пълен чайник ще може да се справи сам със задачата в следващите час-два!

Непрекъснатост на функцията. Точки на прекъсване и тяхната класификация

Понятие за непрекъснатост на функцията

Нека разгледаме някаква функция, която е непрекъсната на цялата числова ос:

Или, казано по-накратко, нашата функция е непрекъсната върху (множеството от реални числа).

Какъв е "филистимският" критерий за приемственост? Очевидно графикът непрекъсната функцияможе да се рисува, без да се вдига моливът от хартията.

В този случай трябва ясно да се разграничат две прости понятия: област на функцияИ непрекъснатост на функцията. IN общ случай не е едно и също нещо. Например:

Тази функция е дефинирана на цялата числова линия, тоест за всекиЗначението на “x” има собствено значение на “y”. По-специално, ако , тогава . Обърнете внимание, че другата точка е с препинателна точка, тъй като според дефиницията на функция стойността на аргумента трябва да съответства на единственото нещостойност на функцията. По този начин, домейннашата функция: .

въпреки това тази функция не е непрекъснато включена!Съвсем очевидно е, че в момента тя страда празнина. Терминът също е доста разбираем и визуален; наистина, тук моливът така или иначе ще трябва да бъде откъснат от хартията. Малко по-късно ще разгледаме класификацията на точките на прекъсване.

Непрекъснатост на функция в точка и на интервал

В конкретен математически проблем можем да говорим за непрекъснатост на функция в точка, непрекъснатост на функция в интервал, полуинтервал или непрекъснатост на функция в сегмент. Това е, няма "обикновена приемственост"– функцията може да бъде непрекъсната НЯКЪДЕ. И основният „градивен елемент“ на всичко останало е непрекъснатост на функцията в точката .

Теория математически анализдава дефиниция на непрекъснатостта на функция в точка, използвайки "делта" и "епсилон" околности, но на практика се използва друга дефиниция, на която ще обърнем голямо внимание.

Първо да си спомним едностранни границикоито нахлуха в живота ни в първия урок относно функционалните графики. Помислете за ежедневна ситуация:

Ако приближим оста до точката наляво(червена стрелка), тогава съответните стойности на „игрите“ ще вървят по оста до точката (пурпурна стрелка). Математически този факт се фиксира с помощта на ляво ограничение:

Обърнете внимание на записа (чете се „x клони към ka отляво“). „Добавката“ „минус нула“ символизира , по същество това означава, че приближаваме числото от лявата страна.

По същия начин, ако се приближите до точката „ка“ на дясно(синя стрелка), тогава „игрите“ ще достигнат същата стойност, но по зелената стрелка и дясна границаще бъде форматиран, както следва:

„Добавка“ символизира , а записът гласи: „x клони към ka отдясно.“

Ако едностранните граници са крайни и равни(както в нашия случай): , тогава ще кажем, че има ОБЩА граница. Просто е, общото ограничение е нашето „обичайно“ граница на функция, равно на крайно число.

Имайте предвид, че ако функцията не е дефинирана в (пробиване черна точкана клона на графиката), тогава горните изчисления остават валидни. Както вече беше отбелязано няколко пъти, по-специално в статията върху безкрайно малки функции, изразите означават, че "x" безкрайно близосе доближава до точката, докато НЯМА ЗНАЧЕНИЕ, дали самата функция е дефинирана в дадена точка или не. Добър примерще се появи в следващия параграф, когато функцията се анализира.

Определение: функция е непрекъсната в точка, ако границата на функцията в дадена точка е равна на стойността на функцията в тази точка: .

Дефиницията е подробно описана в следните условия:

1) Функцията трябва да бъде дефинирана в точката, тоест стойността трябва да съществува.

2) Трябва да има обща граница на функцията. Както беше отбелязано по-горе, това предполага наличието и равенството на едностранни ограничения: .

3) Границата на функцията в дадена точка трябва да бъде равна на стойността на функцията в тази точка: .

Ако се наруши поне единот трите условия, тогава функцията губи свойството на непрекъснатост в точката .

Непрекъснатост на функция върху интервале формулиран гениално и много просто: една функция е непрекъсната на интервала, ако е непрекъсната във всяка точка от дадения интервал.

По-специално, много функции са непрекъснати в безкраен интервал, т.е. в множеството от реални числа. Това е линейна функция, полиноми, експоненциал, синус, косинус и т.н. И като цяло всяка елементарна функциянепрекъснато на своя област на дефиниция, например, логаритмична функция е непрекъсната на интервала . Надявам се да в този моментимате доста добра представа как изглеждат графиките на основните функции. | Повече ▼ подробна информациятяхната приемственост може да бъде извлечена от любезен човекс фамилното име Фихтенголц.

С непрекъснатостта на функция на сегмент и полуинтервали, всичко също не е трудно, но е по-подходящо да се говори за това в клас относно намирането на минималните и максималните стойности на функция в сегмент, но засега нека не се тревожим за това.

Класификация на точките на прекъсване

Увлекателният живот на функциите е богат на всякакви специални точки, а точките на прекъсване са само една от страниците на тяхната биография.

Забележка : за всеки случай ще се спра на елементарен момент: точката на пречупване е винаги единична точка– няма „няколко точки на прекъсване подред“, тоест няма такова нещо като „интервал на прекъсване“.

Тези точки от своя страна са разделени на две големи групи: разкъсвания от първи видИ разкъсвания от втори вид. Всеки тип празнина има своя собствена характеристикикоито ще разгледаме в момента:

Точка на прекъсване от първи род

Ако условието за непрекъснатост е нарушено в точка и едностранни ограничения краен , тогава се нарича точка на прекъсване от първи род.

Да започнем с най-оптимистичния случай. Според първоначалната идея на урока, исках да разкажа теорията „в общ изглед”, но за да демонстрирам реалността на материала, се спрях на варианта с конкретни герои.

Тъжно е като снимка на младоженци на фона на Вечния огън, но следният кадър е общоприет. Нека изобразим графиката на функцията на чертежа:


Тази функция е непрекъсната на цялата числова ос, с изключение на точката. И всъщност знаменателят не може да бъде равен на нула. Въпреки това, в съответствие със значението на границата, можем безкрайно близосе приближават до „нула“ както отляво, така и отдясно, тоест съществуват едностранни граници и очевидно съвпадат:
(Условие № 2 за приемственост е изпълнено).

Но функцията не е дефинирана в точката, следователно, условие № 1 за непрекъснатост е нарушено и функцията претърпява прекъсване в тази точка.

Прекъсване от този тип (със съществуващите общ лимит) са наречени ремонтируема празнина. Защо подвижни? Тъй като функцията може предефинирамв точката на счупване:

Изглежда странно? Може би. Но такова обозначение на функцията не противоречи на нищо! Сега празнината е затворена и всички са доволни:


Нека извършим официална проверка:

2) – има общо ограничение;
3)

По този начин и трите условия са изпълнени и функцията е непрекъсната в точка според определението за непрекъснатост на функция в точка.

Въпреки това мразещите матан могат да дефинират функцията по лош начин, например :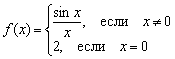


Интересно е, че тук са изпълнени първите две условия за непрекъснатост:
1) – функцията е дефинирана в дадена точка;
2) – има общо ограничение.

Но третата граница не е премината: , тоест границата на функцията в точката не е равностойността на дадена функция в дадена точка.

Така в даден момент функцията претърпява прекъсване.

Вторият, по-тъжен случай се нарича разкъсване от първи вид със скок. И тъгата се предизвиква от едностранчиви ограничения, които крайни и различни. Пример е показан на втория чертеж на урока. Такава празнина обикновено възниква в частично дефинирани функции, които вече бяха споменати в статията относно трансформациите на графиките.

Разгледайте функцията на части и ние ще завършим чертежа му. Как да изградим графика? Много просто. На полуинтервал рисуваме фрагмент от парабола ( зелен цвят), на интервала – права отсечка (червено) и на полуинтервал – права линия ( Син цвят).

Освен това, поради неравенство, стойността се определя за квадратична функция(зелена точка) и поради неравенството стойността се определя за линейна функция(синя точка):

В най-трудния случай трябва да прибягвате до изграждане точка по точка на всяка част от графиката (вижте първата урок за графики на функции).

Сега ще ни интересува само точката. Нека го разгледаме за приемственост:

2) Да изчислим едностранните граници.

Отляво имаме сегмент от червена линия, така че лявата граница е:

Отдясно е синята права линия, а дясната граница:

В резултат на това получихме крайни числа, и те не е равно. Тъй като едностранни ограничения крайни и различни: , тогава нашата функция толерира прекъсване от първи вид със скок.

Логично е, че пропускът не може да бъде премахнат - функцията наистина не може да бъде допълнително дефинирана и „залепена заедно“, както в предишния пример.

Точки на прекъсване от втори род

Обикновено всички други случаи на разкъсване са умело класифицирани в тази категория. Няма да изброявам всичко, защото на практика в 99% от проблемите ще срещнете безкрайна празнина– при лява или дясна ръка и по-често и двете граници са безкрайни.

И, разбира се, най-очевидната картина е хиперболата в точка нула. Тук и двете едностранни граници са безкрайни: , следователно функцията претърпява прекъсване от втори вид в точката .

Опитвам се да напълня статиите си с възможно най-разнообразно съдържание, така че нека да разгледаме графиката на функция, която все още не е срещана:

по стандартната схема:

1) Функцията не е дефинирана в този момент, защото знаменателят отива на нула.

Разбира се, можем веднага да заключим, че функцията претърпява прекъсване в точка , но би било добре да класифицираме естеството на прекъсването, което често се изисква от условието. За това:

Нека ви напомня, че под запис разбираме безкрайно малък отрицателно число , а под записа - безкрайно малко положително число.

Едностранните ограничения са безкрайни, което означава, че функцията претърпява прекъсване от 2-ри вид в точката . Оста y е вертикална асимптотаза графиката.

Не е необичайно да съществуват и двете едностранни граници, но само една от тях е безкрайна, например:

Това е графиката на функцията.

Разглеждаме точката за приемственост:

1) Функцията не е дефинирана на този етап.

2) Нека изчислим едностранните граници:

Ще говорим за метода за изчисляване на такива едностранни граници в последните два примера на лекцията, въпреки че много читатели вече са видели и познали всичко.

Лявата граница е крайна и равна на нула (ние „не отиваме до самата точка“), но дясната граница е безкрайна и оранжевият клон на графиката се приближава безкрайно близо до нейната вертикална асимптота, дадено от уравнението (черна пунктирана линия).

Така че функцията страда втори вид прекъсванев точка .

Що се отнася до прекъсване от 1-ви вид, функцията може да бъде дефинирана в самата точка на прекъсване. Например за частична функция Чувствайте се свободни да поставите черна удебелена точка в началото на координатите. Отдясно има клон на хипербола, а дясната граница е безкрайна. Мисля, че почти всеки има представа как изглежда тази графика.

Това, което всички очакваха с нетърпение:

Как да изследваме функция за непрекъснатост?

Изследването на функция за непрекъснатост в точка се извършва по вече установена рутинна схема, която се състои в проверка на три условия на непрекъснатост:

Пример 1

Функция за изследване

Решение:

1) Единствената точка в обхвата е мястото, където функцията не е дефинирана.

2) Нека изчислим едностранните граници:

Едностранните граници са крайни и равни.

По този начин в момента функцията претърпява отстранимо прекъсване.

Как изглежда графиката на тази функция?

Бих искал да опростя , и изглежда, че се получава обикновена парабола. НОоригиналната функция не е дефинирана в точка, така че се изисква следната клауза:

Да направим чертежа:

Отговор: функцията е непрекъсната на цялата числова ос, с изключение на точката, в която претърпява отстраним прекъсване.

Функцията може да бъде допълнително дефинирана по добър или не толкова добър начин, но според условието това не е задължително.

Казвате, че това е пресилен пример? Въобще не. Това се е случвало десетки пъти в практиката. Почти всички задачи на сайта идват от реална самостоятелна работа и тестове.

Нека се отървем от нашите любими модули:

Пример 2

Функция за изследване за приемственост. Определете естеството на функционалните прекъсвания, ако съществуват. Изпълнете чертежа.

Решение: По някаква причина учениците се страхуват и не харесват функции с модул, въпреки че в тях няма нищо сложно. Вече засегнахме малко такива неща в урока. Геометрични трансформации на графики. Тъй като модулът е неотрицателен, той се разширява, както следва: , където „алфа“ е някакъв израз. IN в такъв случайи нашата функция трябва да бъде написана на части: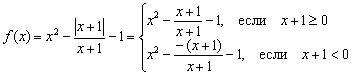

Но дробите на двете парчета трябва да бъдат намалени с . Намаляването, както в предишния пример, няма да се осъществи без последствия. Оригиналната функция не е дефинирана в точката, тъй като знаменателят отива на нула. Следователно системата трябва допълнително да уточни условието и да направи първото неравенство строго:

Сега за МНОГО ПОЛЕЗЕН приемрешения: преди да завършите задачата на чернова, е добре да направите чертеж (независимо дали се изисква от условията или не). Това ще помогне, първо, незабавно да видите точки на непрекъснатост и точки на прекъсване, и, второ, ще ви предпази 100% от грешки при намиране на едностранни граници.

Да направим чертежа. В съответствие с нашите изчисления, отляво на точката е необходимо да се начертае фрагмент от парабола (син цвят), а отдясно - парче от парабола (червен цвят), докато функцията не е дефинирана в самата точка:

Ако се съмнявате, вземете няколко x стойности и ги включете във функцията (не забравяйте, че модулът унищожава възможния знак минус) и проверете графиката.

Нека разгледаме аналитично функцията за непрекъснатост:

1) Функцията не е дефинирана в точката, така че веднага можем да кажем, че не е непрекъсната в нея.

2) Нека установим естеството на прекъсването; за да направим това, изчисляваме едностранни граници:

Едностранните граници са крайни и различни, което означава, че функцията претърпява прекъсване от 1-ви вид със скок в точката . Обърнете внимание отново, че когато намирате ограничения, няма значение дали функцията в точката на прекъсване е дефинирана или не.

Сега остава само да прехвърлите чертежа от черновата (направен е сякаш с помощта на проучване ;-)) и да изпълните задачата:

Отговор: функцията е непрекъсната на цялата числова ос, с изключение на точката, в която претърпява прекъсване от първи вид със скок.

Понякога те изискват допълнителна индикация за скока на прекъсване. Изчислява се просто - от дясната граница трябва да извадите лявата граница: , тоест в точката на прекъсване нашата функция скочи с 2 единици надолу (както ни казва знакът минус).

Пример 3

Функция за изследване за приемственост. Определете естеството на функционалните прекъсвания, ако съществуват. Направете рисунка.

Това е пример, който можете да решите сами, примерно решение в края на урока.

Нека да преминем към най-популярната и разпространена версия на задачата, когато функцията се състои от три части:

Пример 4

Изследвайте функция за непрекъснатост и начертайте графика на функцията .

Решение: очевидно е, че и трите части на функцията са непрекъснати на съответните интервали, така че остава да се проверят само две точки на „свързване“ между частите. Първо, нека направим чернова на чертеж, коментирах техниката на изграждане достатъчно подробно в първата част на статията. Единственото нещо е, че трябва внимателно да следваме нашите особени точки: поради неравенството стойността принадлежи на правата линия (зелена точка), а поради неравенството стойността принадлежи на параболата (червена точка):


Е, по принцип всичко е ясно =) Остава само да формализираме решението. За всяка от двете точки на „съединяване“ стандартно проверяваме 3 условия за непрекъснатост:

аз)Проверяваме точката за приемственост

1)

Едностранните граници са крайни и различни, което означава, че функцията претърпява прекъсване от 1-ви вид със скок в точката .

Нека изчислим скока на прекъсване като разликата между дясната и лявата граница:
, тоест графиката рязко се повиши с една единица.

II)Проверяваме точката за приемственост

1) – функцията е дефинирана в дадена точка.

2) Намерете едностранни ограничения:

– едностранните граници са крайни и равни, което означава, че има обща граница.

3) – границата на функция в точка е равна на стойността на тази функция в дадена точка.

На последния етап прехвърляме чертежа в окончателния вариант, след което поставяме последния акорд:

Отговор: функцията е непрекъсната на цялата числова ос, с изключение на точката, в която претърпява прекъсване от първи род със скок.

Пример 5

Изследвайте функцията за непрекъснатост и постройте нейната графика .

Това е пример, който можете да решите сами, кратко решениеи примерен образец на задачата в края на урока.

Може да останете с впечатлението, че в един момент функцията трябва да е непрекъсната, а в друг трябва да има прекъсване. На практика това не винаги е така. Опитайте се да не пренебрегвате останалите примери - ще има няколко интересни и важни функции:

Пример 6

Дадена функция . Изследвайте функцията за непрекъснатост в точки. Постройте графика.

Решение: и отново веднага изпълнете чертежа върху черновата:

Особеността на тази графика е, че частичната функция е дадена от уравнението на абсцисната ос. Тази област е начертана тук зелено, а в бележника обикновено се подчертава с удебелен шрифт с обикновен молив. И, разбира се, не забравяйте за нашите овни: стойността принадлежи на допирателната клонка (червена точка), а стойността принадлежи на правата линия.

Всичко е ясно от чертежа - функцията е непрекъсната по цялата числова линия, остава само да се формализира решението, което се довежда до пълна автоматизация буквално след 3-4 подобни примера:

аз)Проверяваме точката за приемственост

1) – функцията е дефинирана в дадена точка.

2) Нека изчислим едностранните граници:

, което означава, че има общо ограничение.

За всеки случай нека ви напомня един тривиален факт: границата на константата е равна на самата константа. В този случай границата на нула е равна на самата нула (лява граница).

3) – границата на функция в точка е равна на стойността на тази функция в дадена точка.

По този начин една функция е непрекъсната в точка според дефиницията за непрекъснатост на функция в точка.

II)Проверяваме точката за приемственост

1) – функцията е дефинирана в дадена точка.

2) Намерете едностранни ограничения:

И тук – границата на единица е равна на самата единица.

– има общо ограничение.

3) – границата на функция в точка е равна на стойността на тази функция в дадена точка.

По този начин една функция е непрекъсната в точка според дефиницията за непрекъснатост на функция в точка.

Както обикновено, след проучване прехвърляме нашия чертеж в окончателния вариант.

Отговор: функцията е непрекъсната в точките.

Моля, имайте предвид, че в условието не бяхме попитани нищо относно изучаването на цялата функция за непрекъснатост и се счита за добра математическа форма за формулиране точно и ясноотговорът на поставения въпрос. Между другото, ако условието не изисква да изградите графика, значи имате всяко правоне го изграждайте (въпреки че учителят може да ви принуди да го направите по-късно).

Малка математическа „свирка на езиците“, за да я решите сами:

Пример 7

Дадена функция . Изследвайте функцията за непрекъснатост в точки. Класифицирайте точките на прекъсване, ако има такива. Изпълнете чертежа.

Опитайте се да „произнесете“ всички „думи“ правилно =) И начертайте графиката по-точно, точност, няма да е излишно навсякъде;-)

Както си спомняте, препоръчах незабавно да завършите чертежа като чернова, но от време на време се натъквате на примери, при които не можете веднага да разберете как изглежда графиката. Следователно в някои случаи е изгодно първо да се намерят едностранни граници и едва след това, въз основа на изследването, да се изобразят клоните. В последните два примера ще научим и техника за изчисляване на някои едностранни ограничения:

Пример 8

Проверете функцията за непрекъснатост и изградете нейната схематична графика.

Решение: лошите точки са очевидни: (намалява знаменателя на степента до нула) и (намалява знаменателя на цялата дроб до нула). Не е ясно как изглежда графиката на тази функция, което означава, че е по-добре първо да направите някои изследвания.