एक संख्या जो दशमलव के रूप में होती है। भिन्नात्मक संख्या का दशमलव अंकन

इस ट्यूटोरियल में हम इनमें से प्रत्येक ऑपरेशन को अलग से देखेंगे।

पाठ सामग्री

दशमलव जोड़ना

जैसा कि हम जानते हैं, दशमलव भिन्न में एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव जोड़ते समय पूर्णांक और भिन्नात्मक भाग अलग-अलग जोड़े जाते हैं।

उदाहरण के लिए, आइए दशमलव भिन्न 3.2 और 5.3 जोड़ें। किसी कॉलम में दशमलव भिन्नों को जोड़ना अधिक सुविधाजनक है।

आइए पहले इन दो भिन्नों को एक कॉलम में लिखें, जिसमें पूर्णांक भाग आवश्यक रूप से पूर्णांक के अंतर्गत हों, और भिन्नात्मक भाग भिन्नात्मक के अंतर्गत हों। स्कूल में इस आवश्यकता को कहा जाता है "अल्पविराम के अंतर्गत अल्पविराम".

आइए भिन्नों को एक कॉलम में लिखें ताकि अल्पविराम अल्पविराम के नीचे रहे:

हम भिन्नात्मक भागों को जोड़ना शुरू करते हैं: 2 + 3 = 5। हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम पूरे भाग को जोड़ते हैं: 3 + 5 = 8. हम अपने उत्तर के पूरे भाग में आठ लिखते हैं:

अब हम पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं। ऐसा करने के लिए हम फिर से नियम का पालन करते हैं "अल्पविराम के अंतर्गत अल्पविराम":

हमें 8.5 का उत्तर मिला. अतः व्यंजक 3.2 + 5.3, 8.5 के बराबर है

वास्तव में, सब कुछ उतना सरल नहीं है जितना पहली नज़र में लगता है। यहां नुकसान भी हैं, जिनके बारे में हम अभी बात करेंगे।

दशमलव में स्थान

सामान्य संख्याओं की तरह दशमलव भिन्नों के भी अपने अंक होते हैं। ये दसवें के स्थान, सौवें के स्थान, हजारवें के स्थान हैं। इस मामले में, अंक दशमलव बिंदु के बाद शुरू होते हैं।

दशमलव बिंदु के बाद का पहला अंक दसवें स्थान के लिए जिम्मेदार है, दशमलव बिंदु के बाद दूसरा अंक सौवें स्थान के लिए, और दशमलव बिंदु के बाद तीसरा अंक हजारवें स्थान के लिए जिम्मेदार है।

दशमलव भिन्नों में कुछ स्थान होते हैं उपयोगी जानकारी. विशेष रूप से, वे आपको बताते हैं कि एक दशमलव में कितने दसवें, सौवें और हज़ारवें भाग होते हैं।

उदाहरण के लिए, दशमलव अंश 0.345 पर विचार करें

वह स्थिति जहां तीनों स्थित हैं, कहलाती है दसवाँ स्थान

वह स्थिति जहां चारों स्थित हैं, कहलाती है सौवां स्थान

वह स्थिति जहां पांच स्थित हैं, कहलाती है हज़ारवाँ स्थान

आइए इस चित्र को देखें. हम देखते हैं कि दसवें स्थान पर तीन है। इसका मतलब यह है कि दशमलव भिन्न 0.345 में तीन दसवें भाग होते हैं।

यदि हम भिन्नों को जोड़ते हैं, तो हमें मूल दशमलव भिन्न 0.345 प्राप्त होता है

यह देखा जा सकता है कि पहले तो हमें उत्तर मिला, लेकिन हमने इसे दशमलव अंश में बदल दिया और 0.345 प्राप्त हुआ।

दशमलव भिन्नों को जोड़ते समय उन्हीं सिद्धांतों और नियमों का पालन किया जाता है जैसे सामान्य संख्याओं को जोड़ते समय किया जाता है। दशमलव भिन्नों का योग अंकों में होता है: दसवें को दसवें में जोड़ा जाता है, सौवें को सौवें में, हजारवें को हजारवें में जोड़ा जाता है।

इसलिए, दशमलव भिन्नों को जोड़ते समय, आपको नियम का पालन करना चाहिए "अल्पविराम के अंतर्गत अल्पविराम". अल्पविराम के अंतर्गत अल्पविराम वही क्रम प्रदान करता है जिसमें दसवें को दसवें, सौवें को सौवें, हजारवें को हजारवें में जोड़ा जाता है।

उदाहरण 1।व्यंजक 1.5 + 3.4 का मान ज्ञात कीजिए

सबसे पहले, हम भिन्नात्मक भाग 5 + 4 = 9 जोड़ते हैं। हम अपने उत्तर के भिन्नात्मक भाग में नौ लिखते हैं:

अब हम पूर्णांक भाग 1 + 3 = 4 जोड़ते हैं। हम अपने उत्तर के पूर्णांक भाग में चार लिखते हैं:

अब हम पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं। ऐसा करने के लिए, हम फिर से "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हैं:

हमें 4.9 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 1.5 + 3.4 का मान 4.9 है

उदाहरण 2.व्यंजक का मान ज्ञात कीजिए: 3.51 + 1.22

हम इस अभिव्यक्ति को "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं।

सबसे पहले, हम भिन्नात्मक भाग को जोड़ते हैं, अर्थात् 1+2=3 का सौवां भाग। हम अपने उत्तर के सौवें भाग में त्रिक लिखते हैं:

अब दशमांश 5+2=7 जोड़ें। हम अपने उत्तर के दसवें भाग में सात लिखते हैं:

अब हम पूरे भागों को जोड़ते हैं 3+1=4. हम अपने उत्तर के पूरे भाग में चार लिखते हैं:

हम "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए, पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं:

हमें जो उत्तर मिला वह 4.73 था। इसका मतलब है कि अभिव्यक्ति 3.51 + 1.22 का मान 4.73 के बराबर है

3,51 + 1,22 = 4,73

नियमित संख्याओं की तरह, दशमलव जोड़ते समय, . इस मामले में, उत्तर में एक अंक लिखा जाता है, और बाकी को अगले अंक में स्थानांतरित कर दिया जाता है।

उदाहरण 3.व्यंजक 2.65 + 3.27 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को कॉलम में लिखते हैं:

सौवें भाग को जोड़ें 5+7=12. संख्या 12 हमारे उत्तर के सौवें भाग में फिट नहीं बैठेगी। इसलिए, सौवें भाग में हम संख्या 2 लिखते हैं, और इकाई को अगले अंक पर ले जाते हैं:

अब हम 6+2=8 का दसवां हिस्सा और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 9 मिलता है। हम अपने उत्तर के दसवें में संख्या 9 लिखते हैं:

अब हम पूरे भागों को जोड़ते हैं 2+3=5. हम अपने उत्तर के पूर्णांक भाग में संख्या 5 लिखते हैं:

हमें जो उत्तर मिला वह 5.92 था। इसका मतलब है कि अभिव्यक्ति 2.65 + 3.27 का मान 5.92 के बराबर है

2,65 + 3,27 = 5,92

उदाहरण 4.व्यंजक 9.5 + 2.8 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को कॉलम में लिखते हैं

हम भिन्नात्मक भाग 5 + 8 = 13 जोड़ते हैं। संख्या 13 हमारे उत्तर के भिन्नात्मक भाग में फिट नहीं होगी, इसलिए हम पहले संख्या 3 लिखते हैं, और इकाई को अगले अंक में ले जाते हैं, या यों कहें कि इसे स्थानांतरित करते हैं। पूर्णांक भाग:

अब हम पूर्णांक भाग 9+2=11 और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 12 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 12 लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें उत्तर 12.3 प्राप्त हुआ। इसका मतलब है कि अभिव्यक्ति 9.5 + 2.8 का मान 12.3 है

9,5 + 2,8 = 12,3

दशमलव जोड़ते समय, दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान होनी चाहिए। यदि पर्याप्त संख्याएँ नहीं हैं, तो भिन्नात्मक भाग में ये स्थान शून्य से भरे हुए हैं।

उदाहरण 5. व्यंजक का मान ज्ञात कीजिए: 12.725 + 1.7

इस अभिव्यक्ति को एक कॉलम में लिखने से पहले, आइए दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान कर लें। दशमलव भिन्न 12.725 में दशमलव बिंदु के बाद तीन अंक होते हैं, लेकिन भिन्न 1.7 में केवल एक अंक होता है। इसका मतलब है कि भिन्न 1.7 में आपको अंत में दो शून्य जोड़ने होंगे। तब हमें भिन्न 1.700 प्राप्त होता है। अब आप इस अभिव्यक्ति को एक कॉलम में लिख सकते हैं और गणना शुरू कर सकते हैं:

हजारवें भाग को जोड़ें 5+0=5. हम अपने उत्तर के हज़ारवें भाग में संख्या 5 लिखते हैं:

सैकड़ावाँ भाग 2+0=2 जोड़ें। हम अपने उत्तर के सौवें भाग में संख्या 2 लिखते हैं:

दहाई जोड़ें 7+7=14. संख्या 14 हमारे उत्तर के दसवें हिस्से में फिट नहीं बैठेगी। इसलिए, हम पहले संख्या 4 लिखते हैं, और इकाई को अगले अंक पर ले जाते हैं:

अब हम पूर्णांक भाग 12+1=13 और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 14 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 14 लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 14,425 की प्रतिक्रिया मिली। इसका मतलब है कि अभिव्यक्ति 12.725+1.700 का मान 14.425 है

12,725+ 1,700 = 14,425

दशमलव घटाना

दशमलव अंशों को घटाते समय, आपको उन्हीं नियमों का पालन करना चाहिए जो जोड़ते समय करते हैं: "दशमलव बिंदु के नीचे अल्पविराम" और "दशमलव बिंदु के बाद अंकों की समान संख्या।"

उदाहरण 1।व्यंजक 2.5 − 2.2 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं:

हम भिन्नात्मक भाग 5−2=3 की गणना करते हैं। हम अपने उत्तर के दसवें भाग में संख्या 3 लिखते हैं:

हम पूर्णांक भाग 2−2=0 की गणना करते हैं। हम अपने उत्तर के पूर्णांक भाग में शून्य लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 0.3 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 2.5 − 2.2 का मान 0.3 के बराबर है

2,5 − 2,2 = 0,3

उदाहरण 2.व्यंजक 7.353 - 3.1 का मान ज्ञात कीजिए

इस अभिव्यक्ति में दशमलव स्थानों की भिन्न संख्या है। भिन्न 7.353 में दशमलव बिंदु के बाद तीन अंक होते हैं, लेकिन भिन्न 3.1 में केवल एक अंक होता है। इसका मतलब यह है कि भिन्न 3.1 में आपको दोनों भिन्नों में अंकों की संख्या समान बनाने के लिए अंत में दो शून्य जोड़ने की आवश्यकता है। तो हमें 3,100 मिलते हैं.

अब आप इस अभिव्यक्ति को एक कॉलम में लिख सकते हैं और इसकी गणना कर सकते हैं:

हमें 4,253 की प्रतिक्रिया मिली। इसका मतलब है कि अभिव्यक्ति 7.353 - 3.1 का मान 4.253 के बराबर है

7,353 — 3,1 = 4,253

सामान्य संख्याओं की तरह, यदि घटाव असंभव हो जाए तो कभी-कभी आपको आसन्न अंक से एक अंक उधार लेना होगा।

उदाहरण 3.व्यंजक 3.46 − 2.39 का मान ज्ञात कीजिए

6−9 का सौवाँ भाग घटाएँ। आप संख्या 6 में से संख्या 9 नहीं घटा सकते। इसलिए, आपको आसन्न अंक में से एक अंक उधार लेना होगा। आसन्न अंक में से एक को उधार लेने पर, संख्या 6 संख्या 16 में बदल जाती है। अब आप 16−9=7 के सौवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के सौवें भाग में सात लिखते हैं:

अब हम दसवाँ भाग घटाते हैं। चूँकि हमने दसवें स्थान पर एक इकाई ले ली, इसलिए वहाँ स्थित आंकड़ा एक इकाई कम हो गया। दूसरे शब्दों में, दसवें स्थान पर अब संख्या 4 नहीं, बल्कि संख्या 3 है। आइए 3−3=0 के दसवें हिस्से की गणना करें। हम अपने उत्तर के दसवें भाग में शून्य लिखते हैं:

अब हम पूर्ण भाग 3−2=1 घटाते हैं। हम अपने उत्तर के पूर्णांक भाग में एक लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 1.07 का उत्तर मिला. इसका मतलब है कि व्यंजक 3.46−2.39 का मान 1.07 के बराबर है

3,46−2,39=1,07

उदाहरण 4. व्यंजक 3−1.2 का मान ज्ञात कीजिए

यह उदाहरण एक पूर्ण संख्या से दशमलव घटाता है। आइए इस अभिव्यक्ति को एक कॉलम में लिखें ताकि संपूर्ण भागदशमलव अंश 1.23 संख्या 3 निकला

अब दशमलव बिंदु के बाद अंकों की संख्या समान कर लेते हैं। ऐसा करने के लिए, संख्या 3 के बाद हम अल्पविराम लगाते हैं और एक शून्य जोड़ते हैं:

अब हम दसवां हिस्सा घटाते हैं: 0−2. आप शून्य में से संख्या 2 नहीं घटा सकते। इसलिए, आपको आसन्न अंक में से एक अंक लेना होगा। पड़ोसी अंक से एक उधार लेने पर, 0 संख्या 10 में बदल जाता है। अब आप 10−2=8 के दसवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के दसवें भाग में आठ लिखते हैं:

अब हम पूरे भागों को घटाते हैं। पहले, संख्या 3 संपूर्ण में स्थित थी, लेकिन हमने इसमें से एक इकाई ले ली। परिणामस्वरूप, यह संख्या 2 में बदल गया। इसलिए, 2 से हम 1 घटाते हैं। 2−1=1। हम अपने उत्तर के पूर्णांक भाग में एक लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें जो उत्तर मिला वह 1.8 था। इसका मतलब है कि व्यंजक 3−1.2 का मान 1.8 है

दशमलव को गुणा करना

दशमलव को गुणा करना सरल भी है और मज़ेदार भी। दशमलव को गुणा करने के लिए, आप अल्पविरामों को अनदेखा करते हुए, उन्हें नियमित संख्याओं की तरह गुणा करें।

उत्तर प्राप्त करने के बाद, आपको पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी, फिर उत्तर में दाईं ओर से समान अंकों की संख्या गिननी होगी और अल्पविराम लगाना होगा।

उदाहरण 1।व्यंजक 2.5 × 1.5 का मान ज्ञात कीजिए

आइए अल्पविरामों को अनदेखा करते हुए, इन दशमलव भिन्नों को सामान्य संख्याओं की तरह गुणा करें। अल्पविरामों को अनदेखा करने के लिए, आप अस्थायी रूप से कल्पना कर सकते हैं कि वे पूरी तरह से अनुपस्थित हैं:

हमें 375 मिला। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.5 और 1.5 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। पहले भिन्न में दशमलव बिंदु के बाद एक अंक होता है, और दूसरे भिन्न में भी एक अंक होता है। कुल दो नंबर.

हम संख्या 375 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 3.75 का उत्तर मिला. अतः व्यंजक 2.5 × 1.5 का मान 3.75 है

2.5 × 1.5 = 3.75

उदाहरण 2.व्यंजक 12.85 × 2.7 का मान ज्ञात कीजिए

आइए अल्पविरामों को अनदेखा करते हुए, इन दशमलव भिन्नों को गुणा करें:

हमें 34695 मिला। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 12.85 और 2.7 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 12.85 में दशमलव बिंदु के बाद दो अंक होते हैं, और भिन्न 2.7 में एक अंक होता है - कुल तीन अंक।

हम संख्या 34695 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 34,695 का रिस्पॉन्स मिला. अतः व्यंजक 12.85 × 2.7 का मान 34.695 है

12.85 × 2.7 = 34.695

दशमलव को एक नियमित संख्या से गुणा करना

कभी-कभी ऐसी स्थितियाँ उत्पन्न होती हैं जब आपको दशमलव भिन्न को किसी नियमित संख्या से गुणा करने की आवश्यकता होती है।

दशमलव और संख्या को गुणा करने के लिए, आप दशमलव में अल्पविराम पर ध्यान दिए बिना उन्हें गुणा करते हैं। उत्तर प्राप्त करने के बाद, आपको पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव भिन्न में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी, फिर उत्तर में दाईं ओर से अंकों की समान संख्या गिननी होगी और अल्पविराम लगाना होगा।

उदाहरण के लिए, 2.54 को 2 से गुणा करें

अल्पविराम को अनदेखा करते हुए, दशमलव भिन्न 2.54 को सामान्य संख्या 2 से गुणा करें:

हमें संख्या 508 मिली। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.54 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 2.54 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 508 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 5.08 का उत्तर मिला. अतः व्यंजक 2.54 × 2 का मान 5.08 है

2.54 × 2 = 5.08

दशमलव को 10, 100, 1000 से गुणा करना

दशमलव को 10, 100, या 1000 से गुणा करना उसी तरह से किया जाता है जैसे दशमलव को नियमित संख्याओं से गुणा करना। आपको दशमलव अंश में अल्पविराम पर ध्यान न देते हुए गुणन करना है, फिर उत्तर में, पूरे भाग को भिन्नात्मक भाग से अलग करना है, दाईं ओर से अंकों की उतनी ही संख्या गिननी है जितनी दशमलव बिंदु के बाद अंक थे।

उदाहरण के लिए, 2.88 को 10 से गुणा करें

दशमलव भिन्न में अल्पविराम को अनदेखा करते हुए, दशमलव भिन्न 2.88 को 10 से गुणा करें:

हमें 2880 मिला। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.88 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। हम देखते हैं कि भिन्न 2.88 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 2880 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 28.80 का जवाब मिला. आइए अंतिम शून्य को हटा दें और 28.8 प्राप्त करें। इसका मतलब है कि अभिव्यक्ति 2.88×10 का मान 28.8 है

2.88 × 10 = 28.8

दशमलव भिन्नों को 10, 100, 1000 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। इसमें दशमलव बिंदु को दाईं ओर उतने अंकों तक ले जाना शामिल है जितने गुणनखंड में शून्य हैं।

उदाहरण के लिए, आइए पिछले उदाहरण 2.88×10 को इस प्रकार हल करें। कोई गणना दिए बिना, हम तुरंत कारक 10 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें एक शून्य है। अब भिन्न 2.88 में हम दशमलव बिंदु को दाएँ एक अंक तक ले जाते हैं, हमें 28.8 प्राप्त होता है।

2.88 × 10 = 28.8

आइए 2.88 को 100 से गुणा करने का प्रयास करें। हम तुरंत कारक 100 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें दो शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को दाएँ दो अंकों तक ले जाते हैं, हमें 288 प्राप्त होता है

2.88 × 100 = 288

आइए 2.88 को 1000 से गुणा करने का प्रयास करें। हम तुरंत कारक 1000 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाते हैं। वहां कोई तीसरा अंक नहीं है, इसलिए हम एक और शून्य जोड़ते हैं। परिणामस्वरूप, हमें 2880 मिलते हैं।

2.88 × 1000 = 2880

दशमलव को 0.1 0.01 और 0.001 से गुणा करना

दशमलव को 0.1, 0.01, और 0.001 से गुणा करना उसी तरह काम करता है जैसे दशमलव को दशमलव से गुणा करना। भिन्नों को सामान्य संख्याओं की तरह गुणा करना और उत्तर में अल्पविराम लगाना, दाहिनी ओर उतने ही अंक गिनना आवश्यक है जितने दोनों भिन्नों में दशमलव बिंदु के बाद अंक हों।

उदाहरण के लिए, 3.25 को 0.1 से गुणा करें

हम इन भिन्नों को सामान्य संख्याओं की तरह गुणा करते हैं, अल्पविरामों को अनदेखा करते हुए:

हमें 325 मिला। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 3.25 और 0.1 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 3.25 में दशमलव बिंदु के बाद दो अंक होते हैं, और भिन्न 0.1 में एक अंक होता है। कुल तीन नंबर.

हम संख्या 325 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है। तीन अंक गिनने के बाद पता चलता है कि अंक खत्म हो गए हैं। इस मामले में, आपको एक शून्य जोड़ना होगा और अल्पविराम जोड़ना होगा:

हमें 0.325 का उत्तर मिला। इसका मतलब है कि अभिव्यक्ति 3.25 × 0.1 का मान 0.325 है

3.25 × 0.1 = 0.325

दशमलव को 0.1, 0.01 और 0.001 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। इसमें दशमलव बिंदु को बाईं ओर उतने अंकों तक ले जाना शामिल है जितने गुणनखंड में शून्य हैं।

उदाहरण के लिए, आइए पिछले उदाहरण 3.25 × 0.1 को इस प्रकार हल करें। बिना कोई गणना दिए हम तुरंत 0.1 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें एक शून्य है। अब भिन्न 3.25 में हम दशमलव बिंदु को एक अंक से बाईं ओर ले जाते हैं। अल्पविराम को एक अंक बाईं ओर ले जाने पर, हम देखते हैं कि तीन से पहले कोई और अंक नहीं हैं। इस स्थिति में, एक शून्य जोड़ें और अल्पविराम लगाएं। परिणाम 0.325 है

3.25 × 0.1 = 0.325

आइए 3.25 को 0.01 से गुणा करने का प्रयास करें। हम तुरंत 0.01 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें दो शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को बाएँ दो अंकों पर ले जाते हैं, हमें 0.0325 मिलता है

3.25 × 0.01 = 0.0325

आइए 3.25 को 0.001 से गुणा करने का प्रयास करें। हम तुरंत 0.001 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को तीन अंकों से बाईं ओर ले जाते हैं, हमें 0.00325 मिलता है

3.25 × 0.001 = 0.00325

दशमलव भिन्नों को 0.1, 0.001 और 0.001 से गुणा करने को 10, 100, 1000 से गुणा करने में भ्रमित न हों। सामान्य गलतीज्यादातर लोग।

10, 100, 1000 से गुणा करने पर, दशमलव बिंदु दाईं ओर उतने ही अंकों से चला जाता है जितने गुणक में शून्य होते हैं।

और जब 0.1, 0.01 और 0.001 से गुणा किया जाता है, तो दशमलव बिंदु बाईं ओर उतने ही अंकों से चला जाता है, क्योंकि गुणक में शून्य होते हैं।

यदि शुरुआत में याद रखना कठिन हो, तो आप पहली विधि का उपयोग कर सकते हैं, जिसमें सामान्य संख्याओं की तरह गुणा किया जाता है। उत्तर में आपको दाहिनी ओर के अंकों की समान संख्या गिनकर पूर्ण भाग को भिन्नात्मक भाग से अलग करना होगा क्योंकि दोनों भिन्नों में दशमलव बिंदु के बाद अंक होते हैं।

छोटी संख्या को बड़ी संख्या से भाग देना। अग्रवर्ती स्तर।

पिछले पाठों में से एक में, हमने कहा था कि जब एक छोटी संख्या को बड़ी संख्या से विभाजित किया जाता है, तो एक भिन्न प्राप्त होता है, जिसका अंश लाभांश होता है, और हर भाजक होता है।

उदाहरण के लिए, एक सेब को दो के बीच विभाजित करने के लिए, आपको अंश में 1 (एक सेब) लिखना होगा, और हर में 2 (दो दोस्त) लिखना होगा। परिणामस्वरूप, हमें भिन्न प्राप्त होता है। इसका मतलब है कि प्रत्येक मित्र को एक सेब मिलेगा। दूसरे शब्दों में, आधा सेब. भिन्न समस्या का उत्तर है "एक सेब को दो भागों में कैसे बाँटें"

यह पता चलता है कि यदि आप 1 को 2 से विभाजित करते हैं तो आप इस समस्या को और अधिक हल कर सकते हैं। आखिरकार, किसी भी भिन्न में भिन्नात्मक रेखा का अर्थ विभाजन होता है, और इसलिए भिन्न में इस विभाजन की अनुमति है। आख़िर कैसे? हम इस तथ्य के आदी हैं कि लाभांश हमेशा भाजक से बड़ा होता है। लेकिन यहां, इसके विपरीत, लाभांश भाजक से कम है।

यदि हम यह याद रखें कि अंश का अर्थ कुचलना, विभाजन करना, विभाजन करना है तो सब कुछ स्पष्ट हो जाएगा। इसका मतलब यह है कि इकाई को केवल दो भागों में नहीं, बल्कि जितने चाहें उतने भागों में विभाजित किया जा सकता है।

जब आप किसी छोटी संख्या को बड़ी संख्या से विभाजित करते हैं, तो आपको एक दशमलव अंश मिलता है जिसमें पूर्णांक भाग 0 (शून्य) होता है। भिन्नात्मक भाग कुछ भी हो सकता है।

तो, आइए 1 को 2 से विभाजित करें। आइए इस उदाहरण को एक कोने से हल करें:

एक को पूर्णतः दो भागों में विभाजित नहीं किया जा सकता। यदि आप कोई प्रश्न पूछते हैं "एक में कितने दो होते हैं" , तो उत्तर 0 होगा। इसलिए, भागफल में हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब, हमेशा की तरह, शेषफल प्राप्त करने के लिए हम भागफल को भाजक से गुणा करते हैं:

वह क्षण आ गया है जब इकाई को दो भागों में विभाजित किया जा सकता है। ऐसा करने के लिए, परिणामी शून्य के दाईं ओर एक और शून्य जोड़ें:

हमें 10 प्राप्त हुआ। 10 को 2 से विभाजित करने पर, हमें 5 प्राप्त होता है। हम पाँच को अपने उत्तर के भिन्नात्मक भाग में लिखते हैं:

अब हम गणना पूरी करने के लिए अंतिम शेषफल निकालते हैं। 10 प्राप्त करने के लिए 5 को 2 से गुणा करें

हमें 0.5 का उत्तर मिला. अतः भिन्न 0.5 है

दशमलव अंश 0.5 का उपयोग करके आधा सेब भी लिखा जा सकता है। यदि हम इन दो हिस्सों (0.5 और 0.5) को जोड़ दें, तो हमें फिर से असली पूरा सेब मिलता है:

यह बात तब भी समझ में आ सकती है जब आप कल्पना करें कि 1 सेमी को दो भागों में कैसे विभाजित किया जाता है। यदि आप 1 सेंटीमीटर को 2 भागों में विभाजित करते हैं, तो आपको 0.5 सेमी मिलता है

उदाहरण 2.व्यंजक 4:5 का मान ज्ञात कीजिए

एक चार में कितनी पाँच होती हैं? बिल्कुल नहीं। हम भागफल में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम चार के नीचे एक शून्य लिखते हैं। इस शून्य को लाभांश से तुरंत घटा दें:

अब चारों को 5 भागों में बाँटना शुरू करते हैं। ऐसा करने के लिए, 4 के दाईं ओर एक शून्य जोड़ें और 40 को 5 से विभाजित करें, हमें 8 मिलता है। हम भागफल में आठ लिखते हैं।

हम 40 प्राप्त करने के लिए 8 को 5 से गुणा करके उदाहरण पूरा करते हैं:

हमें 0.8 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 4:5 का मान 0.8 है

उदाहरण 3.व्यंजक 5:125 का मान ज्ञात कीजिए

पाँच में 125 कितनी संख्याएँ हैं? बिल्कुल नहीं। हम भागफल में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम पाँच के नीचे 0 लिखते हैं। पांच में से तुरंत 0 घटाएं

अब पाँचों को 125 भागों में बाँटना शुरू करते हैं। ऐसा करने के लिए, हम इन पाँच के दाईं ओर एक शून्य लिखते हैं:

50 को 125 से भाग दें। संख्या 50 में 125 कितनी संख्याएँ हैं? बिल्कुल नहीं। अतः भागफल में हम पुनः 0 लिखते हैं

0 को 125 से गुणा करें, हमें 0 मिलता है। इस शून्य को 50 के नीचे लिखें। तुरंत 50 में से 0 घटा दें

अब संख्या 50 को 125 भागों में विभाजित करें। ऐसा करने के लिए, हम 50 के दाईं ओर एक और शून्य लिखते हैं:

500 को 125 से विभाजित करें। संख्या 500 में 125 कितनी संख्याएँ हैं? संख्या 500 में चार संख्याएँ 125 हैं। चारों को भागफल में लिखें:

हम 500 प्राप्त करने के लिए 4 को 125 से गुणा करके उदाहरण पूरा करते हैं

हमें 0.04 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 5:125 का मान 0.04 है

बिना किसी शेषफल के संख्याओं को विभाजित करना

तो, चलिए भागफल में इकाई के बाद अल्पविराम लगाते हैं, जिससे यह संकेत मिलता है कि पूर्णांक भागों का विभाजन समाप्त हो गया है और हम भिन्नात्मक भाग की ओर आगे बढ़ रहे हैं:

आइए शेषफल 4 में शून्य जोड़ें

अब 40 को 5 से विभाजित करें, हमें 8 प्राप्त होता है। हम भागफल में आठ लिखते हैं:

40−40=0. हमें 0 बचा है. इसका मतलब है कि विभाजन पूरी तरह से पूरा हो गया है। 9 को 5 से विभाजित करने पर दशमलव भिन्न 1.8 प्राप्त होता है:

9: 5 = 1,8

उदाहरण 2. 84 को बिना किसी शेषफल के 5 से विभाजित करें

सबसे पहले, 84 को हमेशा की तरह शेषफल के साथ 5 से विभाजित करें:

हमें निजी तौर पर 16 मिल गए और 4 और बचे हैं। आइए अब इस शेषफल को 5 से विभाजित करें। भागफल में अल्पविराम लगाएं, और शेष 4 में 0 जोड़ें

अब हम 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम दशमलव बिंदु के बाद भागफल में आठ लिखते हैं:

और यह जांच कर उदाहरण पूरा करें कि क्या अभी भी कुछ शेष है:

दशमलव को एक नियमित संख्या से विभाजित करना

जैसा कि हम जानते हैं, दशमलव भिन्न में एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव अंश को किसी नियमित संख्या से विभाजित करते समय, आपको सबसे पहले यह करना होगा:

• दशमलव भिन्न के पूरे भाग को इस संख्या से विभाजित करें;
• पूरे भाग को विभाजित करने के बाद, आपको तुरंत भागफल में अल्पविराम लगाना होगा और सामान्य विभाजन की तरह गणना जारी रखनी होगी।

उदाहरण के लिए, 4.8 को 2 से विभाजित करें

आइए इस उदाहरण को एक कोने में लिखें:

अब पूरे भाग को 2 से विभाजित करते हैं। चार को दो से विभाजित करने पर दो बराबर होता है। हम भागफल में दो लिखते हैं और तुरंत अल्पविराम लगाते हैं:

अब हम भागफल को भाजक से गुणा करते हैं और देखते हैं कि भाग से कोई शेषफल बचता है या नहीं:

4−4=0. शेषफल शून्य है. हम अभी तक शून्य नहीं लिखते हैं, क्योंकि समाधान पूरा नहीं हुआ है। इसके बाद, हम सामान्य विभाजन की तरह गणना करना जारी रखेंगे। 8 को हटाएं और इसे 2 से विभाजित करें

8: 2 = 4. हम भागफल में चार लिखते हैं और तुरंत इसे भाजक से गुणा करते हैं:

हमें 2.4 का उत्तर मिला. व्यंजक 4.8:2 का मान 2.4 है

उदाहरण 2.व्यंजक 8.43:3 का मान ज्ञात कीजिए

8 को 3 से विभाजित करने पर हमें 2 प्राप्त होता है। 2 के तुरंत बाद अल्पविराम लगाएं:

अब हम भागफल को भाजक 2 × 3 = 6 से गुणा करते हैं। हम आठ के नीचे छह लिखते हैं और शेषफल ज्ञात करते हैं:

24 को 3 से भाग देने पर 8 प्राप्त होता है। हम भागफल में आठ लिखते हैं। भाग का शेषफल ज्ञात करने के लिए इसे तुरंत भाजक से गुणा करें:

24−24=0. शेषफल शून्य है. हम अभी तक शून्य नहीं लिखते हैं। हम लाभांश से अंतिम तीन हटाते हैं और 3 से विभाजित करते हैं, हमें 1 मिलता है। इस उदाहरण को पूरा करने के लिए तुरंत 1 को 3 से गुणा करें:

हमें जो उत्तर मिला वह 2.81 था। इसका अर्थ है कि व्यंजक 8.43:3 का मान 2.81 है

दशमलव को दशमलव से विभाजित करना

किसी दशमलव भिन्न को दशमलव भिन्न से विभाजित करने के लिए, आपको लाभांश और भाजक में दशमलव बिंदु को दाईं ओर उतने ही अंकों से ले जाना होगा जितना कि भाजक में दशमलव बिंदु के बाद होता है, और फिर सामान्य संख्या से विभाजित करना होगा।

उदाहरण के लिए, 5.95 को 1.7 से विभाजित करें

आइए इस अभिव्यक्ति को एक कोने से लिखें

अब लाभांश और भाजक में हम दशमलव बिंदु को दाईं ओर उतने ही अंकों से ले जाते हैं जितने अंक भाजक में दशमलव बिंदु के बाद होते हैं। भाजक में दशमलव बिंदु के बाद एक अंक होता है। इसका मतलब यह है कि लाभांश और भाजक में हमें दशमलव बिंदु को एक अंक से दाईं ओर ले जाना होगा। हम हस्तांतरण:

दशमलव बिंदु को दाएँ एक अंक तक ले जाने के बाद, दशमलव भिन्न 5.95, भिन्न 59.5 बन गया। और दशमलव भिन्न 1.7, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, सामान्य संख्या 17 में बदल गया। और हम पहले से ही जानते हैं कि दशमलव भिन्न को एक नियमित संख्या से कैसे विभाजित किया जाता है। आगे की गणना कठिन नहीं है:

विभाजन को आसान बनाने के लिए अल्पविराम को दाईं ओर ले जाया जाता है। इसकी अनुमति इसलिए है क्योंकि लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित करने पर भागफल नहीं बदलता है। इसका मतलब क्या है?

ये एक है दिलचस्प विशेषताएंविभाजन। इसे भागफल गुण कहा जाता है। अभिव्यक्ति 9: 3 = 3 पर विचार करें। यदि इस अभिव्यक्ति में लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित किया जाता है, तो भागफल 3 नहीं बदलेगा।

आइए लाभांश और भाजक को 2 से गुणा करें और देखें कि इससे क्या निकलता है:

(9 × 2) : (3 × 2) = 18: 6 = 3

जैसा कि उदाहरण से देखा जा सकता है, भागफल नहीं बदला है।

यही बात तब होती है जब हम लाभांश और भाजक में अल्पविराम लगाते हैं। पिछले उदाहरण में, जहां हमने 5.91 को 1.7 से विभाजित किया था, हमने लाभांश और भाजक में अल्पविराम को एक अंक दाईं ओर ले जाया था। दशमलव बिंदु को स्थानांतरित करने के बाद, अंश 5.91 को अंश 59.1 में बदल दिया गया और अंश 1.7 को सामान्य संख्या 17 में बदल दिया गया।

दरअसल, इस प्रक्रिया के अंदर 10 से गुणा होता था। यह इस तरह दिखता था:

5.91 × 10 = 59.1

इसलिए, भाजक में दशमलव बिंदु के बाद अंकों की संख्या यह निर्धारित करती है कि लाभांश और भाजक को किससे गुणा किया जाएगा। दूसरे शब्दों में, भाजक में दशमलव बिंदु के बाद अंकों की संख्या यह निर्धारित करेगी कि लाभांश में कितने अंक और भाजक में दशमलव बिंदु दाईं ओर ले जाया जाएगा।

दशमलव को 10, 100, 1000 से विभाजित करना

दशमलव को 10, 100, या 1000 से विभाजित करना उसी तरह किया जाता है जैसे। उदाहरण के लिए, 2.1 को 10 से विभाजित करें। एक कोने का उपयोग करके इस उदाहरण को हल करें:

लेकिन एक दूसरा तरीका भी है. यह हल्का है. इस पद्धति का सार यह है कि लाभांश में अल्पविराम को उतने अंकों से बाईं ओर ले जाया जाता है जितने भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस प्रकार हल करें। 2.1:10. हम भाजक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। इसका मतलब है कि 2.1 के लाभांश में आपको दशमलव बिंदु को एक अंक से बाईं ओर ले जाना होगा। हम अल्पविराम को बाएँ एक अंक पर ले जाते हैं और देखते हैं कि कोई और अंक नहीं बचा है। इस स्थिति में, संख्या से पहले एक और शून्य जोड़ें। परिणामस्वरूप हमें 0.21 प्राप्त होता है

आइए 2.1 को 100 से विभाजित करने का प्रयास करें। 100 में दो शून्य हैं। इसका मतलब है कि लाभांश 2.1 में हमें अल्पविराम को दो अंकों से बाईं ओर ले जाना होगा:

2,1: 100 = 0,021

आइए 2.1 को 1000 से विभाजित करने का प्रयास करें। 1000 में तीन शून्य होते हैं। इसका मतलब है कि लाभांश 2.1 में आपको अल्पविराम को तीन अंकों से बाईं ओर ले जाना होगा:

2,1: 1000 = 0,0021

दशमलव को 0.1, 0.01 और 0.001 से विभाजित करना

दशमलव अंश को 0.1, 0.01, और 0.001 से विभाजित करना उसी तरह से किया जाता है। लाभांश और भाजक में, आपको दशमलव बिंदु को दाईं ओर उतने अंकों तक ले जाना होगा जितने अंक भाजक में दशमलव बिंदु के बाद हों।

उदाहरण के लिए, आइए 6.3 को 0.1 से विभाजित करें। सबसे पहले, आइए लाभांश और भाजक में अल्पविरामों को दाईं ओर उतने ही अंकों से ले जाएँ जितने अंकों की संख्या भाजक में दशमलव बिंदु के बाद होती है। भाजक में दशमलव बिंदु के बाद एक अंक होता है। इसका मतलब है कि हम लाभांश और भाजक में अल्पविराम को एक अंक से दाईं ओर ले जाते हैं।

दशमलव बिंदु को दाएँ एक अंक पर ले जाने के बाद, दशमलव भिन्न 6.3 सामान्य संख्या 63 बन जाता है, और दशमलव भिन्न 0.1 दशमलव बिंदु को दाएँ एक अंक पर ले जाने के बाद एक में बदल जाता है। और 63 को 1 से विभाजित करना बहुत सरल है:

इसका मतलब है कि अभिव्यक्ति 6.3: 0.1 का मान 63 है

लेकिन एक दूसरा तरीका भी है. यह हल्का है. इस पद्धति का सार यह है कि लाभांश में अल्पविराम को उतने अंकों से दाईं ओर ले जाया जाता है जितने भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस प्रकार हल करें। 6.3: 0.1. आइए भाजक को देखें. हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। इसका मतलब है कि 6.3 के लाभांश में आपको दशमलव बिंदु को एक अंक से दाईं ओर ले जाना होगा। अल्पविराम को दाएँ एक अंक पर ले जाएँ और 63 प्राप्त करें

आइए 6.3 को 0.01 से विभाजित करने का प्रयास करें। 0.01 के भाजक में दो शून्य होते हैं। इसका मतलब है कि लाभांश 6.3 में हमें दशमलव बिंदु को दो अंकों से दाईं ओर ले जाना होगा। लेकिन लाभांश में दशमलव बिंदु के बाद केवल एक अंक होता है। इस स्थिति में, आपको अंत में एक और शून्य जोड़ना होगा। परिणामस्वरूप हमें 630 मिलते हैं

आइए 6.3 को 0.001 से विभाजित करने का प्रयास करें। 0.001 के भाजक में तीन शून्य होते हैं। इसका मतलब है कि लाभांश 6.3 में हमें दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाना होगा:

6,3: 0,001 = 6300

स्वतंत्र समाधान के लिए कार्य

क्या आपको पाठ पसंद आया?
हमारा शामिल करें नया समूह VKontakte और नए पाठों के बारे में सूचनाएं प्राप्त करना प्रारंभ करें

हम इस सामग्री को दशमलव भिन्न जैसे महत्वपूर्ण विषय पर समर्पित करेंगे। सबसे पहले, आइए बुनियादी परिभाषाओं को परिभाषित करें, उदाहरण दें और दशमलव अंकन के नियमों पर ध्यान दें, साथ ही दशमलव भिन्नों के अंक क्या हैं। इसके बाद, हम मुख्य प्रकारों पर प्रकाश डालते हैं: परिमित और अनंत, आवधिक और गैर-आवधिक भिन्न। अंतिम भाग में हम दिखाएंगे कि भिन्नात्मक संख्याओं के संगत बिंदु निर्देशांक अक्ष पर कैसे स्थित होते हैं।

Yandex.RTB R-A-339285-1

भिन्नात्मक संख्याओं का दशमलव अंकन क्या है?

भिन्नात्मक संख्याओं के तथाकथित दशमलव अंकन का उपयोग प्राकृतिक और भिन्नात्मक दोनों संख्याओं के लिए किया जा सकता है। यह दो या दो से अधिक संख्याओं के समूह जैसा दिखता है जिनके बीच अल्पविराम है।

पूर्ण भाग को भिन्नात्मक भाग से अलग करने के लिए दशमलव बिंदु की आवश्यकता होती है। एक नियम के रूप में, दशमलव अंश का अंतिम अंक शून्य नहीं होता है, जब तक कि दशमलव बिंदु पहले शून्य के तुरंत बाद दिखाई न दे।

दशमलव अंकन में भिन्नात्मक संख्याओं के कुछ उदाहरण क्या हैं? यह 34, 21, 0, 35035044, 0, 0001, 11,231,552, 9, आदि हो सकता है।

कुछ पाठ्यपुस्तकों में आप अल्पविराम के बजाय एक अवधि का उपयोग पा सकते हैं (5. 67, 6789. 1011, आदि)। इस विकल्प को समतुल्य माना जाता है, लेकिन यह अंग्रेजी भाषा के स्रोतों के लिए अधिक विशिष्ट है।

दशमलव की परिभाषा

दशमलव अंकन की उपरोक्त अवधारणा के आधार पर, हम दशमलव भिन्नों की निम्नलिखित परिभाषा तैयार कर सकते हैं:

परिभाषा 1

दशमलव दशमलव अंकन में भिन्नात्मक संख्याओं का प्रतिनिधित्व करते हैं।

हमें भिन्नों को इस रूप में लिखने की आवश्यकता क्यों है? यह हमें सामान्य अंकन की तुलना में कुछ लाभ देता है, उदाहरण के लिए, एक अधिक संक्षिप्त अंकन, विशेष रूप से ऐसे मामलों में जहां हर में 1000, 100, 10, आदि या एक मिश्रित संख्या होती है। उदाहरण के लिए, 6 10 के स्थान पर हम 0.6, 25 के स्थान पर 10000 - 0.0023, 512 3 100 के स्थान पर - 512.03 निर्दिष्ट कर सकते हैं।

दशमलव रूप में हर में दहाई, सैकड़ों, हजारों के साथ सामान्य भिन्नों को सही ढंग से कैसे दर्शाया जाए, इस पर एक अलग सामग्री में चर्चा की जाएगी।

दशमलव को सही तरीके से कैसे पढ़ें

दशमलव अंकन पढ़ने के लिए कुछ नियम हैं। इस प्रकार, वे दशमलव अंश जो उनके नियमित सामान्य समकक्षों के अनुरूप होते हैं, लगभग उसी तरह पढ़े जाते हैं, लेकिन शुरुआत में "शून्य दसवां" शब्द जोड़ने के साथ। इस प्रकार, प्रविष्टि 0, 14, जो 14,100 से मेल खाती है, को "शून्य दशमलव चौदह सौवां" के रूप में पढ़ा जाता है।

यदि दशमलव भिन्न को मिश्रित संख्या के साथ जोड़ा जा सकता है, तो इसे इस संख्या के समान ही पढ़ा जाता है। इसलिए, यदि हमारे पास अंश 56, 002 है, जो 56 2 1000 से मेल खाता है, तो हम इस प्रविष्टि को "छप्पन दशमलव दो हजारवें" के रूप में पढ़ते हैं।

दशमलव अंश में किसी अंक का अर्थ इस बात पर निर्भर करता है कि वह कहाँ स्थित है (प्राकृतिक संख्याओं के मामले में भी ऐसा ही है)। तो, दशमलव अंश 0.7 में, सात दसवां है, 0.0007 में यह दस हजारवां है, और अंश 70,000.345 में इसका मतलब सात दसियों हजार पूर्ण इकाइयाँ हैं। इस प्रकार, दशमलव भिन्नों में स्थानीय मान की अवधारणा भी होती है।

दशमलव बिंदु से पहले स्थित अंकों के नाम प्राकृतिक संख्याओं के समान होते हैं। बाद में स्थित लोगों के नाम तालिका में स्पष्ट रूप से प्रस्तुत किए गए हैं:

आइए एक उदाहरण देखें.

उदाहरण 1

हमारे पास दशमलव भिन्न 43,098 है। उसके पास दहाई के स्थान पर चार, इकाई के स्थान पर तीन, दसवें स्थान पर शून्य, सौवें स्थान पर 9 और हजारवें स्थान पर 8 अंक हैं।

दशमलव भिन्नों की श्रेणियों को प्राथमिकता के आधार पर अलग करने की प्रथा है। यदि हम संख्याओं को बाएँ से दाएँ ओर ले जाएँ, तो हम सबसे महत्वपूर्ण से सबसे कम महत्वपूर्ण की ओर चले जाएँगे। यह पता चला है कि सैकड़ों दसियों से पुराने हैं, और प्रति मिलियन भाग सौवें से छोटे हैं। यदि हम उस अंतिम दशमलव अंश को लेते हैं जिसे हमने ऊपर उदाहरण के रूप में उद्धृत किया है, तो इसमें उच्चतम, या उच्चतम, स्थान सैकड़ों का स्थान होगा, और सबसे कम, या सबसे कम, स्थान 10-हजारवाँ स्थान होगा।

किसी भी दशमलव अंश को अलग-अलग अंकों में विस्तारित किया जा सकता है, अर्थात योग के रूप में प्रस्तुत किया जा सकता है। यह क्रिया उसी प्रकार की जाती है जैसे के लिए की जाती है प्राकृतिक संख्या.

उदाहरण 2

आइए भिन्न 56, 0455 को अंकों में विस्तारित करने का प्रयास करें।

हमें मिल जाएगा:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

यदि हम योग के गुणों को याद रखें, तो हम इस अंश को अन्य रूपों में प्रस्तुत कर सकते हैं, उदाहरण के लिए, योग 56 + 0, 0455, या 56, 0055 + 0, 4, आदि के रूप में।

अनुवर्ती दशमलव क्या हैं?

ऊपर हमने जिन भिन्नों के बारे में बात की वे सभी परिमित हैं दशमलव. इसका मतलब यह है कि दशमलव बिंदु के बाद अंकों की संख्या सीमित है। आइए परिभाषा निकालें:

परिभाषा 1

अनुगामी दशमलव एक प्रकार का दशमलव अंश है जिसमें दशमलव चिह्न के बाद दशमलव स्थानों की एक सीमित संख्या होती है।

ऐसे भिन्नों के उदाहरण 0, 367, 3, 7, 55, 102567958, 231 032, 49, आदि हो सकते हैं।

इनमें से किसी भी भिन्न को या तो मिश्रित संख्या में बदला जा सकता है (यदि उनके भिन्नात्मक भाग का मान शून्य से भिन्न हो) या सामान्य अंश(शून्य पूर्णांक भाग के साथ)। यह कैसे किया जाता है, इसके लिए हमने एक अलग लेख समर्पित किया है। यहां हम केवल कुछ उदाहरण बताएंगे: उदाहरण के लिए, हम अंतिम दशमलव अंश 5, 63 को 5 63 100 के रूप में घटा सकते हैं, और 0, 2 2 10 (या इसके बराबर कोई अन्य अंश, के लिए) से मेल खाता है। उदाहरण, 4 20 या 1 5.)

लेकिन उलटी प्रक्रिया, यानी. एक सामान्य भिन्न को दशमलव रूप में लिखना हमेशा संभव नहीं हो सकता है। इसलिए, 5 13 को हर 100, 10, आदि के साथ एक समान भिन्न द्वारा प्रतिस्थापित नहीं किया जा सकता है, जिसका अर्थ है कि इससे अंतिम दशमलव अंश प्राप्त नहीं किया जा सकता है।

अनंत दशमलव भिन्नों के मुख्य प्रकार: आवधिक और गैर-आवधिक भिन्न

हमने ऊपर बताया कि परिमित भिन्न कहलाते हैं क्योंकि उनमें दशमलव बिंदु के बाद अंकों की एक सीमित संख्या होती है। हालाँकि, यह अनंत भी हो सकता है, ऐसी स्थिति में भिन्नों को भी अनंत कहा जाएगा।

परिभाषा 2

अनंत दशमलव भिन्न वे हैं जिनमें दशमलव बिंदु के बाद अंकों की अनंत संख्या होती है।

जाहिर है, ऐसी संख्याओं को पूरी तरह से नहीं लिखा जा सकता है, इसलिए हम उनमें से केवल एक भाग को इंगित करते हैं और फिर एक दीर्घवृत्त जोड़ते हैं। यह चिन्ह दशमलव स्थानों के क्रम की अनंत निरंतरता को इंगित करता है। अनंत दशमलव भिन्नों के उदाहरणों में 0, 143346732…, ​​3, 1415989032…, 153, 0245005…, 2, 6666666666…, 69, 748768152… शामिल हैं। वगैरह।

ऐसे अंश की "पूंछ" में न केवल संख्याओं के प्रतीत होने वाले यादृच्छिक अनुक्रम हो सकते हैं, बल्कि निरंतर पुनरावृत्तिएक ही चिह्न या चिह्नों का समूह। दशमलव बिंदु के बाद प्रत्यावर्ती संख्याओं वाली भिन्नों को आवर्त कहा जाता है।

परिभाषा 3

आवधिक दशमलव भिन्न वे अनंत दशमलव भिन्न होते हैं जिनमें दशमलव बिंदु के बाद एक अंक या कई अंकों का समूह दोहराया जाता है। दोहराए जाने वाले भाग को भिन्न का आवर्त कहा जाता है।

उदाहरण के लिए, भिन्न 3, 444444… के लिए। अवधि संख्या 4 होगी, और 76 के लिए, 134134134134... - समूह 134।

किसी आवर्त भिन्न के अंकन में छोड़े जा सकने वाले वर्णों की न्यूनतम संख्या क्या है? आवर्त भिन्नों के लिए संपूर्ण आवर्त को एक बार कोष्ठक में लिखना पर्याप्त होगा। तो, भिन्न 3, 444444... इसे 3, (4), और 76, 134134134134... - 76, (134) के रूप में लिखना सही होगा।

सामान्य तौर पर, कोष्ठक में कई अवधियों वाली प्रविष्टियों का बिल्कुल वही अर्थ होगा: उदाहरण के लिए, आवधिक अंश 0.677777 0.6 (7) और 0.6 (77), आदि के समान है। फॉर्म 0, 67777 (7), 0, 67 (7777), आदि के रिकॉर्ड भी स्वीकार्य हैं।

गलतियों से बचने के लिए, हम अंकन की एकरूपता का परिचय देते हैं। आइए केवल एक अवधि (संख्याओं का सबसे छोटा संभव अनुक्रम) लिखने के लिए सहमत हों, जो दशमलव बिंदु के सबसे करीब है, और इसे कोष्ठक में संलग्न करें।

अर्थात्, उपरोक्त भिन्न के लिए, हम मुख्य प्रविष्टि 0, 6 (7) मानेंगे, और, उदाहरण के लिए, भिन्न 8, 9134343434 के मामले में, हम 8, 91 (34) लिखेंगे।

यदि किसी साधारण भिन्न के हर में ऐसे अभाज्य गुणनखंड हों जो 5 और 2 के बराबर न हों, तो दशमलव अंकन में परिवर्तित करने पर, उनका परिणाम अनंत भिन्न होगा।

सिद्धांत रूप में, हम किसी भी परिमित भिन्न को आवर्त के रूप में लिख सकते हैं। ऐसा करने के लिए, हमें बस दाईं ओर अनंत संख्या में शून्य जोड़ने की जरूरत है। रिकॉर्डिंग में यह कैसा दिखता है? मान लीजिए कि हमारे पास अंतिम भिन्न 45, 32 है। आवधिक रूप में यह 45, 32 (0) जैसा दिखेगा। यह क्रिया संभव है क्योंकि किसी भी दशमलव भिन्न के दाईं ओर शून्य जोड़ने पर उसके बराबर भिन्न प्राप्त होता है।

9 की अवधि वाले आवधिक भिन्नों पर विशेष ध्यान दिया जाना चाहिए, उदाहरण के लिए, 4, 89 (9), 31, 6 (9)। वे 0 की अवधि वाली समान भिन्नों के लिए एक वैकल्पिक संकेतन हैं, इसलिए शून्य अवधि वाली भिन्नों के साथ लिखते समय उन्हें अक्सर बदल दिया जाता है। इस मामले में, अगले अंक के मान में एक जोड़ा जाता है, और (0) कोष्ठक में दर्शाया जाता है। परिणामी संख्याओं की समानता को साधारण भिन्नों के रूप में प्रस्तुत करके आसानी से सत्यापित किया जा सकता है।

उदाहरण के लिए, भिन्न 8, 31 (9) को संगत भिन्न 8, 32 (0) से बदला जा सकता है। या 4, (9) = 5, (0) = 5.

अनंत दशमलव आवर्त भिन्नों का संदर्भ लें भिन्नात्मक संख्याएं. दूसरे शब्दों में, किसी भी आवधिक अंश को एक साधारण अंश के रूप में दर्शाया जा सकता है, और इसके विपरीत।

ऐसे अंश भी हैं जिनमें दशमलव बिंदु के बाद अंतहीन दोहराव वाला क्रम नहीं होता है। इस स्थिति में, उन्हें गैर-आवधिक भिन्न कहा जाता है।

परिभाषा 4

गैर-आवधिक दशमलव अंशों में वे अनंत दशमलव अंश शामिल होते हैं जिनमें दशमलव बिंदु के बाद कोई अवधि नहीं होती है, अर्थात। संख्याओं का दोहराव वाला समूह।

कभी-कभी गैर-आवधिक भिन्न, आवर्त अंशों के समान ही दिखते हैं। उदाहरण के लिए, 9, 03003000300003 ... पहली नज़र में ऐसा लगता है कि यह एक अवधि है, हालाँकि विस्तृत विश्लेषणदशमलव स्थान पुष्टि करता है कि यह अभी भी एक गैर-आवधिक भिन्न है। ऐसे नंबरों से आपको बेहद सावधान रहने की जरूरत है.

गैर-आवधिक भिन्नों को अपरिमेय संख्याओं के रूप में वर्गीकृत किया गया है। वे साधारण भिन्नों में परिवर्तित नहीं होते।

दशमलव के साथ बुनियादी संचालन

निम्नलिखित ऑपरेशन दशमलव अंशों के साथ किए जा सकते हैं: तुलना, घटाव, जोड़, विभाजन और गुणा। आइए उनमें से प्रत्येक को अलग से देखें।

दशमलव की तुलना को मूल दशमलव के अनुरूप भिन्नों की तुलना करने तक कम किया जा सकता है। लेकिन अनंत गैर-आवधिक भिन्नों को इस रूप में नहीं बदला जा सकता है, और दशमलव भिन्नों को साधारण भिन्नों में परिवर्तित करना अक्सर एक श्रम-गहन कार्य होता है। यदि किसी समस्या को हल करते समय हमें ऐसा करने की आवश्यकता हो तो हम तुलनात्मक कार्रवाई कैसे शीघ्रता से कर सकते हैं? जिस प्रकार हम प्राकृतिक संख्याओं की तुलना करते हैं, उसी प्रकार अंकों के आधार पर दशमलव भिन्नों की तुलना करना सुविधाजनक होता है। हम इस पद्धति पर एक अलग लेख समर्पित करेंगे।

कुछ दशमलव भिन्नों को दूसरों के साथ जोड़ने के लिए, प्राकृतिक संख्याओं की तरह, कॉलम जोड़ विधि का उपयोग करना सुविधाजनक होता है। आवधिक दशमलव अंशों को जोड़ने के लिए, आपको पहले उन्हें सामान्य अंशों से बदलना होगा और मानक योजना के अनुसार गिनना होगा। यदि, समस्या की स्थितियों के अनुसार, हमें अनंत गैर-आवधिक भिन्नों को जोड़ने की आवश्यकता है, तो हमें पहले उन्हें एक निश्चित अंक तक पूर्णांकित करना होगा, और फिर उन्हें जोड़ना होगा। हम जिस अंक को जितना छोटा करेंगे, गणना की सटीकता उतनी ही अधिक होगी। अनंत भिन्नों को घटाने, गुणा करने तथा भाग देने के लिए पूर्व-पूर्णांकन भी आवश्यक है।

दशमलव भिन्नों के बीच अंतर ज्ञात करना योग का व्युत्क्रम है। अनिवार्य रूप से, घटाव का उपयोग करके हम एक संख्या पा सकते हैं जिसका योग जिस अंश के साथ हम घटा रहे हैं वह हमें वह अंश देगा जिसे हम कम कर रहे हैं। हम इस बारे में एक अलग लेख में अधिक विस्तार से बात करेंगे।

दशमलव भिन्नों को गुणा करना प्राकृतिक संख्याओं की तरह ही किया जाता है। स्तंभ गणना विधि भी इसके लिए उपयुक्त है। हम फिर से पहले से अध्ययन किए गए नियमों के अनुसार आवधिक भिन्नों के साथ इस क्रिया को साधारण भिन्नों के गुणन तक कम कर देते हैं। जैसा कि हमें याद है, अनंत भिन्नों को गणना से पहले पूर्णांकित किया जाना चाहिए।

दशमलव को विभाजित करने की प्रक्रिया गुणा करने की विपरीत प्रक्रिया है। समस्याओं को हल करते समय, हम स्तंभ गणना का भी उपयोग करते हैं।

आप अंतिम दशमलव अंश और निर्देशांक अक्ष पर एक बिंदु के बीच एक सटीक पत्राचार स्थापित कर सकते हैं। आइए जानें कि अक्ष पर एक बिंदु को कैसे चिह्नित किया जाए जो आवश्यक दशमलव अंश के बिल्कुल अनुरूप होगा।

हम पहले ही अध्ययन कर चुके हैं कि साधारण भिन्नों के अनुरूप बिंदु कैसे बनाए जाते हैं, लेकिन दशमलव भिन्नों को इस रूप में घटाया जा सकता है। उदाहरण के लिए, सामान्य अंश 14 10, 1, 4 के समान है, इसलिए संबंधित बिंदु को मूल से सकारात्मक दिशा में बिल्कुल उसी दूरी से हटा दिया जाएगा:

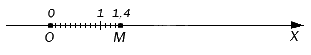
आप दशमलव अंश को साधारण अंश से बदले बिना भी काम कर सकते हैं, लेकिन आधार के रूप में अंकों द्वारा विस्तार की विधि का उपयोग करें। इसलिए, यदि हमें एक बिंदु चिह्नित करना है जिसका निर्देशांक 15, 4008 के बराबर होगा, तो हम पहले इस संख्या को योग 15 + 0, 4 +, 0008 के रूप में प्रस्तुत करेंगे। आरंभ करने के लिए, आइए उलटी गिनती की शुरुआत से सकारात्मक दिशा में 15 संपूर्ण इकाई खंडों को अलग रखें, फिर एक खंड का 4 दसवां हिस्सा, और फिर एक खंड का 8 दस-हजारवां हिस्सा। परिणामस्वरूप, हमें एक समन्वय बिंदु मिलता है जो भिन्न 15, 4008 से मेल खाता है।

अनंत दशमलव अंश के लिए, इस पद्धति का उपयोग करना बेहतर है, क्योंकि यह आपको वांछित बिंदु के जितना करीब चाहें उतना करीब पहुंचने की अनुमति देता है। कुछ मामलों में, निर्देशांक अक्ष पर एक अनंत अंश के लिए सटीक पत्राचार बनाना संभव है: उदाहरण के लिए, 2 = 1, 41421। . . , और यह अंश निर्देशांक किरण पर एक बिंदु से जुड़ा हो सकता है, जो वर्ग के विकर्ण की लंबाई से 0 से दूर है, जिसकी भुजा एक इकाई खंड के बराबर होगी।

यदि हमें अक्ष पर कोई बिंदु नहीं, बल्कि उसके अनुरूप एक दशमलव अंश मिलता है, तो इस क्रिया को किसी खंड का दशमलव माप कहा जाता है। आइए देखें कि इसे सही तरीके से कैसे करें।

मान लीजिए कि हमें शून्य से परे की ओर जाना है इस बिंदुनिर्देशांक अक्ष पर (या अनंत अंश के मामले में जितना संभव हो उतना करीब पहुंचें)। ऐसा करने के लिए, हम धीरे-धीरे इकाई खंडों को मूल बिंदु से तब तक स्थगित करते हैं जब तक हम वांछित बिंदु तक नहीं पहुंच जाते। पूरे खंडों के बाद, यदि आवश्यक हो, तो हम दसवें, सौवें और छोटे अंशों को मापते हैं ताकि मिलान यथासंभव सटीक हो। परिणामस्वरूप, हमें एक दशमलव अंश प्राप्त हुआ जो इसके अनुरूप है दिया गया बिंदुसमन्वय अक्ष पर.

ऊपर हमने बिंदु M के साथ एक चित्र दिखाया है। इसे फिर से देखें: इस बिंदु तक पहुंचने के लिए, आपको एक इकाई खंड और उसके चार दसवें हिस्से को शून्य से मापने की आवश्यकता है, क्योंकि यह बिंदु दशमलव अंश 1, 4 से मेल खाता है।

यदि हम दशमलव माप की प्रक्रिया में किसी बिंदु तक नहीं पहुंच पाते हैं, तो इसका मतलब है कि यह एक अनंत दशमलव अंश से मेल खाता है।

यदि आपको पाठ में कोई त्रुटि दिखाई देती है, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएँ

ऐसा होता है कि गणना की सुविधा के लिए आपको एक साधारण अंश को दशमलव में बदलने की आवश्यकता होती है और इसके विपरीत। हम इस लेख में यह कैसे करें इसके बारे में बात करेंगे। आइए सामान्य भिन्नों को दशमलव में बदलने और इसके विपरीत के नियमों को देखें, और उदाहरण भी दें।

Yandex.RTB R-A-339285-1

हम एक निश्चित क्रम का पालन करते हुए साधारण भिन्नों को दशमलव में बदलने पर विचार करेंगे। सबसे पहले, आइए देखें कि 10 के गुणज वाले हर वाले साधारण भिन्नों को दशमलव में कैसे परिवर्तित किया जाता है: 10, 100, 1000, आदि। ऐसे हर वाले भिन्न, वास्तव में, दशमलव भिन्नों का एक अधिक बोझिल अंकन हैं।

इसके बाद, हम देखेंगे कि केवल 10 के गुणज ही नहीं बल्कि किसी भी हर वाली साधारण भिन्न को दशमलव भिन्न में कैसे बदला जाए। ध्यान दें कि साधारण भिन्नों को दशमलव में परिवर्तित करते समय, न केवल परिमित दशमलव प्राप्त होते हैं, बल्कि अनंत आवधिक दशमलव भिन्न भी प्राप्त होते हैं।

आएँ शुरू करें!

10, 100, 1000 आदि हर वाली साधारण भिन्नों का अनुवाद। दशमलव तक

सबसे पहले, मान लें कि कुछ भिन्नों को दशमलव रूप में परिवर्तित करने से पहले कुछ तैयारी की आवश्यकता होती है। यह क्या है? अंश में संख्या से पहले आपको इतने शून्य जोड़ने होंगे कि अंश में अंकों की संख्या हर में शून्य की संख्या के बराबर हो जाए। उदाहरण के लिए, भिन्न 3100 के लिए, संख्या 0 को अंश में 3 के बाईं ओर एक बार जोड़ा जाना चाहिए। ऊपर बताए गए नियम के अनुसार, अंश 610 में संशोधन की आवश्यकता नहीं है।

आइए एक और उदाहरण देखें, जिसके बाद हम एक नियम बनाएंगे जो पहली बार में उपयोग करने के लिए विशेष रूप से सुविधाजनक है, जबकि भिन्नों को परिवर्तित करने में बहुत अधिक अनुभव नहीं है। तो, अंश में शून्य जोड़ने के बाद भिन्न 1610000 001510000 जैसा दिखेगा।

10, 100, 1000, आदि के हर के साथ एक सामान्य भिन्न को कैसे परिवर्तित करें। दशमलव तक?

साधारण उचित भिन्नों को दशमलव में बदलने का नियम

1. 0 लिखें और उसके बाद अल्पविराम लगाएं।
2. हम अंश-गणक से वह संख्या लिखते हैं जो शून्य जोड़ने पर प्राप्त होती है।

अब आइए उदाहरणों पर चलते हैं।

उदाहरण 1: भिन्नों को दशमलव में बदलना

आइए भिन्न 39,100 को दशमलव में बदलें।

सबसे पहले, हम भिन्न को देखते हैं और देखते हैं कि कोई प्रारंभिक कार्रवाई करने की आवश्यकता नहीं है - अंश में अंकों की संख्या हर में शून्य की संख्या के साथ मेल खाती है।

नियम का पालन करते हुए हम 0 लिखते हैं, उसके बाद दशमलव बिंदु लगाते हैं और अंश से संख्या लिखते हैं। हमें दशमलव भिन्न 0.39 प्राप्त होता है।

आइए इस विषय पर एक अन्य उदाहरण का समाधान देखें।

उदाहरण 2. भिन्नों को दशमलव में बदलना

आइए भिन्न 105 10000000 को दशमलव के रूप में लिखें।

हर में शून्य की संख्या 7 है और अंश में केवल तीन अंक हैं। आइए अंश-गणक में संख्या से पहले 4 और शून्य जोड़ें:

0000105 10000000

अब हम 0 लिखते हैं, उसके बाद दशमलव बिंदु लगाते हैं और अंश से संख्या लिखते हैं। हमें दशमलव अंश 0.0000105 प्राप्त होता है।

सभी उदाहरणों में विचारित भिन्न सामान्य उचित भिन्न हैं। लेकिन आप एक अनुचित भिन्न को दशमलव में कैसे बदलते हैं? आइए तुरंत कहें कि ऐसे भिन्नों के लिए शून्य जोड़ने की तैयारी की कोई आवश्यकता नहीं है। चलिए एक नियम बनाते हैं.

साधारण अनुचित भिन्नों को दशमलव में बदलने का नियम

1. अंश-गणक में जो संख्या है उसे लिखो।
2. हम दाहिनी ओर के उतने अंकों को अलग करने के लिए दशमलव बिंदु का उपयोग करते हैं जितने मूल भिन्न के हर में शून्य होते हैं।

इस नियम का उपयोग कैसे करें इसका एक उदाहरण नीचे दिया गया है।

उदाहरण 3. भिन्नों को दशमलव में बदलना

आइए भिन्न 56888038009 100000 को एक साधारण अनियमित भिन्न से दशमलव में बदलें।

सबसे पहले, आइए अंश-गणक से संख्या लिखें:

अब, दाईं ओर, हम पांच अंकों को दशमलव बिंदु से अलग करते हैं (हर में शून्य की संख्या पांच है)। हम पाते हैं:

अगला प्रश्न जो स्वाभाविक रूप से उठता है वह यह है: एक मिश्रित संख्या को दशमलव भिन्न में कैसे परिवर्तित किया जाए यदि उसके भिन्नात्मक भाग का हर संख्या 10, 100, 1000, आदि है। ऐसी संख्या को दशमलव भिन्न में बदलने के लिए आप निम्नलिखित नियम का उपयोग कर सकते हैं।

मिश्रित संख्याओं को दशमलव में बदलने का नियम

1. यदि आवश्यक हो तो हम संख्या का भिन्नात्मक भाग तैयार करते हैं।
2. हम मूल संख्या का पूरा भाग लिखते हैं और उसके बाद अल्पविराम लगाते हैं।
3. हम भिन्नात्मक भाग के अंश से संख्या को जोड़े गए शून्य के साथ लिखते हैं।

आइए एक उदाहरण देखें.

उदाहरण 4: मिश्रित संख्याओं को दशमलव में बदलना

आइए मिश्रित संख्या 23 17 10000 को दशमलव भिन्न में बदलें।

भिन्नात्मक भाग में हमारे पास अभिव्यक्ति 17 10000 है। आइए इसे तैयार करें और अंश के बाईं ओर दो और शून्य जोड़ें। हमें मिलता है: 0017 10000.

अब हम संख्या का पूरा भाग लिखते हैं और उसके बाद अल्पविराम लगाते हैं: 23, . .

दशमलव बिंदु के बाद अंश-गणक से शून्य सहित संख्या लिखें। हमें परिणाम मिलता है:

23 17 10000 = 23 , 0017

साधारण भिन्नों को परिमित एवं अनंत आवर्त भिन्नों में परिवर्तित करना

निःसंदेह, आप 10, 100, 1000 आदि के बराबर हर वाले दशमलव और साधारण भिन्नों में परिवर्तित कर सकते हैं।

अक्सर एक भिन्न को आसानी से एक नए हर में घटाया जा सकता है, और फिर इस लेख के पहले पैराग्राफ में निर्धारित नियम का उपयोग करें। उदाहरण के लिए, भिन्न 25 के अंश और हर को 2 से गुणा करना पर्याप्त है, और हमें भिन्न 410 मिलता है, जिसे आसानी से दशमलव रूप 0.4 में परिवर्तित किया जा सकता है।

हालाँकि, भिन्न को दशमलव में बदलने की इस विधि का उपयोग हमेशा नहीं किया जा सकता है। नीचे हम विचार करेंगे कि यदि विचारित पद्धति को लागू करना असंभव हो तो क्या करें।

किसी अंश को दशमलव में बदलने का एक मौलिक नया तरीका अंश को एक कॉलम के साथ हर से विभाजित करना है। यह ऑपरेशन प्राकृतिक संख्याओं को एक कॉलम से विभाजित करने के समान है, लेकिन इसकी अपनी विशेषताएं हैं।

विभाजित करते समय अंश को दशमलव अंश के रूप में दर्शाया जाता है - के दाईं ओर पिछले अंकअंश के पहले अल्पविराम लगाया जाता है और शून्य जोड़ा जाता है। परिणामी भागफल में, अंश के पूर्णांक भाग का विभाजन समाप्त होने पर एक दशमलव बिंदु रखा जाता है। यह विधि वास्तव में कैसे काम करती है यह उदाहरणों को देखने के बाद स्पष्ट हो जाएगा।

उदाहरण 5. भिन्नों को दशमलव में बदलना

आइए सामान्य भिन्न 621 4 को दशमलव रूप में बदलें।

आइए अंश-गणक से संख्या 621 को दशमलव भिन्न के रूप में निरूपित करें, दशमलव बिंदु के बाद कुछ शून्य जोड़ें। 621 = 621.00

आइए अब एक कॉलम का उपयोग करके 621.00 को 4 से विभाजित करें। विभाजन के पहले तीन चरण प्राकृतिक संख्याओं को विभाजित करने के समान ही होंगे, और हमें प्राप्त होगा।

जब हम लाभांश में दशमलव बिंदु पर पहुंचते हैं, और शेष शून्य से भिन्न होता है, तो हम भागफल में एक दशमलव बिंदु डालते हैं और विभाजित करना जारी रखते हैं, लाभांश में अल्पविराम पर ध्यान नहीं देते हैं।

परिणामस्वरूप, हमें दशमलव भिन्न 155, 25 प्राप्त होता है, जो सामान्य भिन्न 621 4 को उलटने का परिणाम है।

621 4 = 155 , 25

आइए सामग्री को सुदृढ़ करने के लिए एक और उदाहरण देखें।

उदाहरण 6. भिन्नों को दशमलव में बदलना

आइए सामान्य भिन्न 21 800 को उलट दें।

ऐसा करने के लिए, भिन्न 21,000 को एक कॉलम में 800 से विभाजित करें। पूरे भाग का विभाजन पहले चरण पर समाप्त हो जाएगा, इसलिए इसके तुरंत बाद हम भागफल में एक दशमलव बिंदु डालते हैं और विभाजन जारी रखते हैं, लाभांश में अल्पविराम पर ध्यान नहीं देते जब तक कि हमें शून्य के बराबर शेषफल नहीं मिलता।

परिणामस्वरूप, हमें मिला: 21,800 = 0.02625।

लेकिन क्या होगा यदि विभाजित करने पर भी हमें 0 शेष न मिले। ऐसे मामलों में, विभाजन को अनिश्चित काल तक जारी रखा जा सकता है। हालाँकि, एक निश्चित चरण से शुरू करके, अवशेषों को समय-समय पर दोहराया जाएगा। तदनुसार, भागफल में संख्याएँ दोहराई जाएंगी। इसका मतलब यह है कि एक साधारण भिन्न को दशमलव अनंत आवर्त भिन्न में बदल दिया जाता है। आइये इसे एक उदाहरण से समझाते हैं।

उदाहरण 7. भिन्नों को दशमलव में बदलना

आइए सामान्य भिन्न 19 44 को दशमलव में बदलें। ऐसा करने के लिए, हम कॉलम द्वारा विभाजन करते हैं।

हम देखते हैं कि विभाजन के दौरान, अवशेष 8 और 36 दोहराए जाते हैं। इस स्थिति में, भागफल में संख्याएँ 1 और 8 दोहराई जाती हैं। यह दशमलव अंश में अवधि है. रिकॉर्डिंग करते समय, इन नंबरों को कोष्ठक में रखा जाता है।

इस प्रकार, मूल साधारण अंश एक अनंत आवधिक दशमलव अंश में परिवर्तित हो जाता है।

19 44 = 0 , 43 (18) .

आइए एक अघुलनशील साधारण भिन्न को देखें। यह क्या रूप लेगा? कौन सी साधारण भिन्नों को परिमित दशमलवों में परिवर्तित किया जाता है, और कौन सी भिन्नों को अनंत आवर्त दशमलवों में परिवर्तित किया जाता है?

सबसे पहले, मान लें कि यदि किसी भिन्न को हर 10, 100, 1000... में से किसी एक तक घटाया जा सकता है, तो इसका रूप अंतिम दशमलव भिन्न होगा। किसी भिन्न को इन हरों में से किसी एक में घटाने के लिए, उसका हर 10, 100, 1000 आदि संख्याओं में से कम से कम एक का भाजक होना चाहिए। संख्याओं को अभाज्य गुणनखंडों में विभाजित करने के नियमों से यह निष्कर्ष निकलता है कि संख्याओं का विभाजक 10, 100, 1000, आदि है। जब इसे अभाज्य गुणनखंडों में विभाजित किया जाता है, तो इसमें केवल संख्याएँ 2 और 5 ही होनी चाहिए।

आइए संक्षेप में बताएं कि क्या कहा गया है:

1. एक सामान्य भिन्न को अंतिम दशमलव तक घटाया जा सकता है यदि उसके हर को 2 और 5 के अभाज्य गुणनखंडों में विभाजित किया जा सके।
2. यदि, संख्या 2 और 5 के अलावा, हर के विस्तार में अन्य अभाज्य संख्याएँ हैं, तो भिन्न को अनंत आवधिक दशमलव अंश के रूप में घटा दिया जाता है।

चलिए एक उदाहरण देते हैं.

उदाहरण 8. भिन्नों को दशमलव में बदलना

इनमें से कौन सा अंश 47 20, 7 12, 21 56, 31 17 अंतिम दशमलव अंश में परिवर्तित हो जाता है, और कौन सा - केवल एक आवधिक अंश में। आइए भिन्न को सीधे दशमलव में बदले बिना इस प्रश्न का उत्तर दें।

भिन्न 47 20, जैसा कि देखना आसान है, अंश और हर को 5 से गुणा करके एक नए हर 100 में घटा दिया जाता है।

47 20 = 235 100. इससे हम यह निष्कर्ष निकालते हैं कि यह भिन्न अंतिम दशमलव भिन्न में परिवर्तित हो जाता है।

भिन्न 7 12 के हर का गुणनखंड करने पर 12 = 2 · 2 · 3 प्राप्त होता है। चूँकि अभाज्य गुणनखंड 3, 2 और 5 से भिन्न है, इसलिए इस भिन्न को एक परिमित दशमलव भिन्न के रूप में प्रस्तुत नहीं किया जा सकता है, बल्कि यह एक अनंत आवधिक भिन्न के रूप में होगा।

भिन्न 21 56 को सबसे पहले कम करने की आवश्यकता है। 7 से घटाने के बाद, हमें अपरिवर्तनीय भिन्न 3 8 प्राप्त होता है, जिसके हर का गुणनखंडन करने पर 8 = 2 · 2 · 2 मिलता है। इसलिए, यह अंतिम दशमलव भिन्न है।

भिन्न 31 17 के मामले में, हर का गुणनखंडन अभाज्य संख्या 17 ही है। तदनुसार, इस भिन्न को अनंत आवर्त दशमलव भिन्न में परिवर्तित किया जा सकता है।

एक साधारण अंश को अनंत और गैर-आवधिक दशमलव अंश में परिवर्तित नहीं किया जा सकता है

ऊपर हमने केवल परिमित और अनंत आवर्त भिन्नों के बारे में बात की। लेकिन क्या किसी साधारण भिन्न को अनंत गैर-आवधिक भिन्न में बदला जा सकता है?

हम उत्तर देते हैं: नहीं!

महत्वपूर्ण!

किसी अनंत भिन्न को दशमलव में परिवर्तित करते समय, परिणाम या तो एक परिमित दशमलव या अनंत आवधिक दशमलव होता है।

किसी भाग का शेषफल सदैव भाजक से कम होता है। दूसरे शब्दों में, विभाज्यता प्रमेय के अनुसार, यदि हम किसी प्राकृतिक संख्या को संख्या q से विभाजित करते हैं, तो किसी भी स्थिति में विभाजन का शेष भाग q-1 से अधिक नहीं हो सकता है। विभाजन पूरा होने के बाद, निम्नलिखित स्थितियों में से एक संभव है:

1. हमें 0 का शेषफल मिलता है और यहीं पर विभाजन समाप्त होता है।
2. हमें एक शेषफल मिलता है, जिसे बाद में विभाजित करने पर दोहराया जाता है, जिसके परिणामस्वरूप एक अनंत आवधिक अंश प्राप्त होता है।

भिन्न को दशमलव में परिवर्तित करते समय कोई अन्य विकल्प नहीं हो सकता। आइए यह भी कहें कि एक अनंत आवधिक अंश में अवधि की लंबाई (अंकों की संख्या) हमेशा संबंधित साधारण अंश के हर में अंकों की संख्या से कम होती है।

दशमलव को भिन्नों में बदलना

अब दशमलव भिन्न को सामान्य भिन्न में बदलने की विपरीत प्रक्रिया को देखने का समय आ गया है। आइए हम एक अनुवाद नियम बनाएं जिसमें तीन चरण शामिल हों। दशमलव भिन्न को सामान्य भिन्न में कैसे बदलें?

दशमलव भिन्नों को साधारण भिन्नों में बदलने का नियम

1. अंश में हम मूल दशमलव अंश से संख्या लिखते हैं, अल्पविराम और बाईं ओर के सभी शून्य, यदि कोई हो, को हटा देते हैं।
2. हर में हम एक के बाद उतने ही शून्य लिखते हैं जितने मूल दशमलव अंश में दशमलव बिंदु के बाद अंक होते हैं।
3. यदि आवश्यक हो, तो परिणामी साधारण अंश को कम करें।

आइए आवेदन पर विचार करें इस नियम काउदाहरण सहित.

उदाहरण 8. दशमलव भिन्नों को साधारण भिन्नों में बदलना

आइए संख्या 3.025 की एक साधारण भिन्न के रूप में कल्पना करें।

1. हम दशमलव अंश को अंश में ही लिखते हैं, अल्पविराम को हटाते हुए: 3025।
2. हर में हम एक लिखते हैं, और उसके बाद तीन शून्य - यह दशमलव बिंदु के बाद मूल भिन्न में कितने अंक समाहित हैं: 3025 1000।
3. परिणामी अंश 3025 1000 को 25 से कम किया जा सकता है, जिसके परिणामस्वरूप: 3025 1000 = 121 40।

उदाहरण 9. दशमलव भिन्नों को साधारण भिन्नों में बदलना

आइए भिन्न 0.0017 को दशमलव से साधारण में बदलें।

1. अंश में हम बाईं ओर अल्पविराम और शून्य को हटाकर भिन्न 0, 0017 लिखते हैं। यह 17 साल का हो जाएगा.
2. हम हर में एक लिखते हैं, और उसके बाद हम चार शून्य लिखते हैं: 17 10000। यह अंश अप्रासंगिक है।

यदि दशमलव भिन्न में पूर्णांक भाग हो तो ऐसे भिन्न को तुरंत मिश्रित संख्या में बदला जा सकता है। इसे कैसे करना है?

चलिए एक और नियम बनाते हैं.

दशमलव को मिश्रित संख्या में बदलने का नियम.

1. भिन्न में दशमलव बिंदु से पहले की संख्या को मिश्रित संख्या के पूर्णांक भाग के रूप में लिखा जाता है।
2. अंश में हम भिन्न में दशमलव बिंदु के बाद की संख्या लिखते हैं, बाईं ओर यदि कोई शून्य हो तो उसे हटा देते हैं।
3. भिन्नात्मक भाग के हर में हम एक और उतने ही शून्य जोड़ते हैं जितने भिन्नात्मक भाग में दशमलव बिंदु के बाद अंक होते हैं।

चलिए एक उदाहरण लेते हैं

उदाहरण 10. दशमलव को मिश्रित संख्या में बदलना

आइए भिन्न 155, 06005 की एक मिश्रित संख्या के रूप में कल्पना करें।

1. हम संख्या 155 को पूर्णांक भाग के रूप में लिखते हैं।
2. अंश में हम दशमलव बिंदु के बाद शून्य को हटाकर संख्याएँ लिखते हैं।
3. हम हर में एक और पांच शून्य लिखते हैं

आइए एक मिश्रित संख्या सीखें: 155 6005 100000

भिन्नात्मक भाग को 5 से कम किया जा सकता है। हम इसे छोटा करते हैं और अंतिम परिणाम प्राप्त करते हैं:

155 , 06005 = 155 1201 20000

अनंत आवर्त दशमलवों को भिन्नों में परिवर्तित करना

आइए आवर्ती दशमलव भिन्नों को साधारण भिन्नों में बदलने के उदाहरण देखें। शुरू करने से पहले, आइए स्पष्ट करें: किसी भी आवधिक दशमलव भिन्न को साधारण भिन्न में बदला जा सकता है।

सबसे सरल मामला तब होता है जब भिन्न की अवधि शून्य होती है। शून्य अवधि वाले एक आवधिक अंश को अंतिम दशमलव अंश द्वारा प्रतिस्थापित किया जाता है, और ऐसे अंश को उलटने की प्रक्रिया को अंतिम दशमलव अंश को उलटने तक कम कर दिया जाता है।

उदाहरण 11. एक आवर्त दशमलव भिन्न को सामान्य भिन्न में बदलना

आइए आवर्त भिन्न 3, 75 (0) को उल्टा करें।

दाईं ओर के शून्य को हटाकर, हमें अंतिम दशमलव अंश 3.75 प्राप्त होता है।

पिछले पैराग्राफ में चर्चा किए गए एल्गोरिदम का उपयोग करके इस अंश को एक साधारण अंश में परिवर्तित करने पर, हम प्राप्त करते हैं:

3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .

यदि भिन्न की अवधि शून्य से भिन्न हो तो क्या होगा? आवधिक भाग को ज्यामितीय प्रगति की शर्तों के योग के रूप में माना जाना चाहिए, जो घटता है। आइए इसे एक उदाहरण से समझाएं:

0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

अनंत घटती ज्यामितीय प्रगति के पदों के योग का एक सूत्र है। यदि प्रगति का पहला पद b है और हर q ऐसा है कि 0 है< q < 1 , то сумма равна b 1 - q .

आइए इस सूत्र का उपयोग करके कुछ उदाहरण देखें।

उदाहरण 12. एक आवर्त दशमलव भिन्न को सामान्य भिन्न में बदलना

मान लीजिए हमारे पास एक आवर्त भिन्न 0, (8) है और हमें इसे एक साधारण भिन्न में बदलना है।

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .

यहां हमारे पास अनंत ह्रास है ज्यामितीय अनुक्रमपहले पद 0, 8 और हर 0, 1 के साथ।

आइए सूत्र लागू करें:

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9

यह आवश्यक साधारण अंश है.

सामग्री को समेकित करने के लिए, एक और उदाहरण पर विचार करें।

उदाहरण 13. एक आवर्त दशमलव भिन्न को सामान्य भिन्न में बदलना

आइए भिन्न 0, 43 (18) को उलट दें।

सबसे पहले हम भिन्न को अनंत योग के रूप में लिखते हैं:

0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)

आइए कोष्ठक में शब्दों को देखें। इस ज्यामितीय प्रगति को इस प्रकार दर्शाया जा सकता है:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

हम परिणाम को अंतिम भिन्न 0, 43 = 43 100 में जोड़ते हैं और परिणाम प्राप्त करते हैं:

0 , 43 (18) = 43 100 + 18 9900

इन भिन्नों को जोड़ने और घटाने के बाद, हमें अंतिम उत्तर मिलता है:

0 , 43 (18) = 19 44

इस लेख को समाप्त करने के लिए, हम कहेंगे कि गैर-आवधिक अनंत दशमलव अंशों को साधारण भिन्नों में परिवर्तित नहीं किया जा सकता है।

यदि आपको पाठ में कोई त्रुटि दिखाई देती है, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएँ

यह आलेख निम्न से संबंधित है दशमलव. यहां हम भिन्नात्मक संख्याओं के दशमलव अंकन को समझेंगे, दशमलव भिन्न की अवधारणा का परिचय देंगे और दशमलव भिन्नों के उदाहरण देंगे। आगे हम दशमलव भिन्नों के अंकों के बारे में बात करेंगे और अंकों के नाम देंगे। इसके बाद, हम अनंत दशमलव भिन्नों पर ध्यान केंद्रित करेंगे, आइए आवर्ती और गैर-आवधिक भिन्नों के बारे में बात करते हैं। आगे हम दशमलव भिन्नों के साथ बुनियादी संक्रियाओं को सूचीबद्ध करेंगे। अंत में, आइए हम निर्देशांक बीम पर दशमलव अंशों की स्थिति स्थापित करें।

पेज नेविगेशन.

भिन्नात्मक संख्या का दशमलव अंकन

दशमलव पढ़ना

आइए दशमलव भिन्नों को पढ़ने के नियमों के बारे में कुछ शब्द कहें।

दशमलव भिन्न, जो उचित साधारण भिन्नों के अनुरूप होते हैं, इन साधारण भिन्नों की तरह ही पढ़े जाते हैं, केवल "शून्य पूर्णांक" पहले जोड़ा जाता है। उदाहरण के लिए, दशमलव भिन्न 0.12 सामान्य भिन्न 12/100 ("बारह सौवां" पढ़ें) से मेल खाता है, इसलिए, 0.12 को "शून्य दशमलव बारह सौवां" के रूप में पढ़ा जाता है।

मिश्रित संख्याओं के अनुरूप दशमलव अंश बिल्कुल इन मिश्रित संख्याओं के समान ही पढ़े जाते हैं। उदाहरण के लिए, दशमलव अंश 56.002 एक मिश्रित संख्या से मेल खाता है, इसलिए दशमलव अंश 56.002 को "छप्पन दशमलव दो हजारवें" के रूप में पढ़ा जाता है।

दशमलव में स्थान

दशमलव भिन्नों को लिखने के साथ-साथ प्राकृतिक संख्याओं को लिखने में, प्रत्येक अंक का अर्थ उसकी स्थिति पर निर्भर करता है। दरअसल, दशमलव अंश 0.3 में संख्या 3 का अर्थ है तीन दसवां हिस्सा, दशमलव अंश 0.0003 में - तीन दस हजारवां, और दशमलव अंश 30,000.152 में - तीन दस हजारवां। तो हम बात कर सकते हैं दशमलव स्थानों, साथ ही प्राकृतिक संख्याओं के अंकों के बारे में भी।

दशमलव अंश में दशमलव बिंदु तक के अंकों के नाम प्राकृतिक संख्याओं के अंकों के नाम से पूरी तरह मेल खाते हैं। और दशमलव बिंदु के बाद दशमलव स्थानों के नाम निम्न तालिका से देखे जा सकते हैं।

उदाहरण के लिए, दशमलव अंश 37.051 में, अंक 3 दहाई के स्थान पर है, 7 इकाई के स्थान पर है, 0 दशवें स्थान पर है, 5 सौवें स्थान पर है, और 1 हजारवें स्थान पर है।

दशमलव भिन्नों में स्थान भी पूर्वता में भिन्न होते हैं। यदि दशमलव भिन्न को लिखते समय हम एक अंक से दूसरे अंक पर बाएँ से दाएँ जाते हैं, तो हम आगे बढ़ेंगे वरिष्ठको जूनियर रैंक. उदाहरण के लिए, सैकड़ों का स्थान दसवें स्थान से पुराना है, और लाखों का स्थान सौवें स्थान से निचला है। किसी दिए गए अंतिम दशमलव अंश में, हम बड़े और छोटे अंकों के बारे में बात कर सकते हैं। उदाहरण के लिए, दशमलव भिन्न में 604.9387 वरिष्ठ (उच्चतम)स्थान सैकड़ों स्थान है, और कनिष्ठ (निम्नतम)- दस हजारवाँ अंक।

दशमलव भिन्नों के लिए, अंकों में विस्तार होता है। यह प्राकृतिक संख्याओं के अंकों में विस्तार के समान है। उदाहरण के लिए, 45.6072 के दशमलव स्थानों में विस्तार इस प्रकार है: 45.6072=40+5+0.6+0.007+0.0002. और दशमलव अंश के अंकों में अपघटन से जोड़ के गुण आपको इस दशमलव अंश के अन्य निरूपणों पर जाने की अनुमति देते हैं, उदाहरण के लिए, 45.6072=45+0.6072, या 45.6072=40.6+5.007+0.0002, या 45.6072= 45.0072+ 0.6.

दशमलव को समाप्त करना

इस बिंदु तक, हमने केवल दशमलव भिन्नों के बारे में बात की है, जिनके अंकन में दशमलव बिंदु के बाद अंकों की एक सीमित संख्या होती है। ऐसे भिन्नों को परिमित दशमलव कहा जाता है।

परिभाषा।

दशमलव को समाप्त करना- ये दशमलव अंश हैं, जिनके रिकॉर्ड में वर्णों (अंकों) की एक सीमित संख्या होती है।

यहां अंतिम दशमलव भिन्नों के कुछ उदाहरण दिए गए हैं: 0.317, 3.5, 51.1020304958, 230,032.45।

हालाँकि, प्रत्येक अंश को अंतिम दशमलव के रूप में प्रदर्शित नहीं किया जा सकता है। उदाहरण के लिए, भिन्न 5/13 को 10, 100, ... में से किसी एक हर वाले समान भिन्न से प्रतिस्थापित नहीं किया जा सकता है, इसलिए, इसे अंतिम दशमलव भिन्न में परिवर्तित नहीं किया जा सकता है। हम सामान्य भिन्नों को दशमलव में बदलने के सिद्धांत अनुभाग में इसके बारे में अधिक बात करेंगे।

अनंत दशमलव: आवधिक भिन्न और गैर-आवधिक भिन्न

दशमलव बिंदु के बाद दशमलव अंश लिखने में, आप अंकों की अनंत संख्या की संभावना मान सकते हैं। इस मामले में, हम तथाकथित अनंत दशमलव भिन्नों पर विचार करेंगे।

परिभाषा।

अनंत दशमलव- ये दशमलव भिन्न होते हैं, जिनमें अनंत संख्या में अंक होते हैं।

यह स्पष्ट है कि हम अनंत दशमलव अंशों को पूर्ण रूप में नहीं लिख सकते हैं, इसलिए उनकी रिकॉर्डिंग में हम खुद को दशमलव बिंदु के बाद अंकों की एक निश्चित सीमित संख्या तक ही सीमित रखते हैं और अंकों के अनंत निरंतर अनुक्रम को इंगित करने वाला एक दीर्घवृत्त डालते हैं। यहां अनंत दशमलव भिन्नों के कुछ उदाहरण दिए गए हैं: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.1111111111…, 69.74152152152…।

यदि आप अंतिम दो अनंत दशमलव अंशों को ध्यान से देखें, तो भिन्न 2.11111111... में अंतहीन रूप से दोहराई जाने वाली संख्या 1 स्पष्ट रूप से दिखाई देती है, और अंश 69.74152152152... में, तीसरे दशमलव स्थान से शुरू होकर, संख्याओं का एक दोहराव वाला समूह 1, 5 और 2 साफ़ दिखाई दे रहा है. ऐसी अनंत दशमलव भिन्नों को आवर्त कहा जाता है।

परिभाषा।

आवधिक दशमलव(या केवल आवधिक अंश) अनंत दशमलव अंश हैं, जिनकी रिकॉर्डिंग में, एक निश्चित दशमलव स्थान से शुरू करके, कुछ संख्या या संख्याओं के समूह को अंतहीन रूप से दोहराया जाता है, जिसे कहा जाता है अंश की अवधि.

उदाहरण के लिए, आवर्त भिन्न 2.11111111... की अवधि अंक 1 है, और भिन्न की अवधि 69.74152152152... फॉर्म 152 के अंकों का एक समूह है।

अनंत आवर्त दशमलव भिन्नों के लिए इसे स्वीकार किया जाता है विशेष आकारअभिलेख. संक्षिप्तता के लिए, हम अवधि को एक बार कोष्ठक में बंद करके लिखने पर सहमत हुए। उदाहरण के लिए, आवर्त भिन्न 2.111111111... को 2,(1) के रूप में लिखा जाता है, और आवर्त भिन्न 69.74152152152... को 69.74(152) के रूप में लिखा जाता है।

यह ध्यान देने योग्य है कि समान आवधिक दशमलव अंश के लिए आप निर्दिष्ट कर सकते हैं अलग-अलग अवधि. उदाहरण के लिए, आवधिक दशमलव अंश 0.73333... को 3 की अवधि के साथ अंश 0.7(3) के रूप में माना जा सकता है, और 33 की अवधि के साथ अंश 0.7(33) के रूप में भी माना जा सकता है, और इसी तरह 0.7(333) पर भी विचार किया जा सकता है। 0.7 (3333), ... आप आवर्त भिन्न 0.73333 ... को इस तरह भी देख सकते हैं: 0.733(3), या इस तरह 0.73(333), आदि। यहां, अस्पष्टता और विसंगतियों से बचने के लिए, हम दशमलव अंश की अवधि को दोहराए जाने वाले अंकों के सभी संभावित अनुक्रमों में से सबसे छोटे और निकटतम स्थिति से दशमलव बिंदु तक शुरू करने पर विचार करने के लिए सहमत हैं। अर्थात दशमलव अंश 0.73333... का आवर्त एक अंक 3 का क्रम माना जाएगा और आवर्तिता दशमलव बिंदु के बाद दूसरे स्थान से प्रारंभ होती है, अर्थात 0.73333...=0.7(3)। एक अन्य उदाहरण: आवर्त भिन्न 4.7412121212... का आवर्त 12 है, आवर्तता दशमलव बिंदु के बाद तीसरे अंक से शुरू होती है, अर्थात 4.7412121212...=4.74(12)।

अनंत दशमलव आवर्त भिन्नों को उन साधारण भिन्नों को दशमलव भिन्नों में परिवर्तित करके प्राप्त किया जाता है जिनके हर में 2 और 5 के अलावा अन्य अभाज्य गुणनखंड होते हैं।

यहां 9 की अवधि वाली आवर्ती भिन्नों का उल्लेख करना उचित है। आइए हम ऐसे भिन्नों के उदाहरण दें: 6.43(9) , 27,(9) . ये अंश 0 अवधि वाले आवधिक अंशों के लिए एक और संकेतन हैं, और उन्हें आम तौर पर अवधि 0 के साथ आवधिक अंशों द्वारा प्रतिस्थापित किया जाता है। ऐसा करने के लिए, अवधि 9 को अवधि 0 से बदल दिया जाता है, और अगले उच्चतम अंक का मान एक बढ़ा दिया जाता है। उदाहरण के लिए, फॉर्म 7.24(9) के पीरियड 9 वाले अंश को फॉर्म 7.25(0) के पीरियड 0 वाले आवधिक अंश या समान अंतिम दशमलव अंश 7.25 से बदल दिया जाता है। दूसरा उदाहरण: 4,(9)=5,(0)=5. इन दशमलव भिन्नों को समान साधारण भिन्नों से बदलने के बाद आवर्त 9 वाले भिन्न और आवर्त 0 वाले उसके संगत भिन्न की समानता आसानी से स्थापित हो जाती है।

अंत में, आइए अनंत दशमलव अंशों पर करीब से नज़र डालें, जिनमें अंकों का अंतहीन दोहराव वाला क्रम नहीं होता है। उन्हें गैर-आवधिक कहा जाता है।

परिभाषा।

गैर आवर्ती दशमलव(या केवल गैर-आवधिक भिन्न) अनंत दशमलव भिन्न हैं जिनका कोई आवर्त नहीं है।

कभी-कभी गैर-आवधिक भिन्नों का रूप आवर्त भिन्नों के समान होता है, उदाहरण के लिए, 8.02002000200002... एक गैर-आवधिक भिन्न है। इन मामलों में, आपको अंतर पर ध्यान देने के लिए विशेष रूप से सावधान रहना चाहिए।

ध्यान दें कि गैर-आवधिक भिन्न सामान्य भिन्न में परिवर्तित नहीं होते हैं; अनंत गैर-आवधिक दशमलव भिन्न अपरिमेय संख्याओं का प्रतिनिधित्व करते हैं।

दशमलव के साथ संचालन

दशमलव भिन्नों के साथ संचालन में से एक तुलना है, और चार बुनियादी अंकगणितीय कार्यों को भी परिभाषित किया गया है दशमलव के साथ संचालन: जोड़, घटाव, गुणा और भाग। आइए दशमलव भिन्नों वाली प्रत्येक क्रिया पर अलग से विचार करें।

दशमलव की तुलनाअनिवार्य रूप से तुलना किए जा रहे दशमलव अंशों के अनुरूप सामान्य अंशों की तुलना पर आधारित है। हालाँकि, दशमलव भिन्नों को साधारण भिन्नों में परिवर्तित करना एक श्रम-गहन प्रक्रिया है, और अनंत गैर-आवधिक भिन्नों को साधारण भिन्न के रूप में प्रस्तुत नहीं किया जा सकता है, इसलिए दशमलव भिन्नों की स्थान-वार तुलना का उपयोग करना सुविधाजनक है। दशमलव भिन्नों की स्थान-वार तुलना प्राकृतिक संख्याओं की तुलना के समान है। अधिक विस्तृत जानकारी के लिए, हम लेख का अध्ययन करने की सलाह देते हैं: दशमलव भिन्नों की तुलना, नियम, उदाहरण, समाधान।

चलिए आगे बढ़ते हैं अगला कदम - दशमलव को गुणा करना. परिमित दशमलव भिन्नों का गुणन दशमलव भिन्नों को घटाने, नियम, उदाहरण, प्राकृतिक संख्याओं के एक स्तंभ द्वारा गुणन के समाधान के समान ही किया जाता है। आवधिक भिन्नों के मामले में, गुणन को साधारण भिन्नों के गुणन तक कम किया जा सकता है। बदले में, अनंत गैर-आवधिक दशमलव अंशों का गुणन उनके पूर्णांकन के बाद परिमित दशमलव अंशों के गुणन में कम हो जाता है। हम लेख में आगे के अध्ययन के लिए सामग्री की अनुशंसा करते हैं: दशमलव भिन्नों का गुणन, नियम, उदाहरण, समाधान।

एक निर्देशांक किरण पर दशमलव

अंक और दशमलव के बीच एक-से-एक पत्राचार होता है।

आइए जानें कि निर्देशांक किरण पर बिंदु कैसे बनाए जाते हैं जो किसी दिए गए दशमलव अंश के अनुरूप होते हैं।

हम परिमित दशमलव भिन्नों और अनंत आवधिक दशमलव भिन्नों को समान साधारण भिन्नों से बदल सकते हैं, और फिर निर्देशांक किरण पर संगत साधारण भिन्नों का निर्माण कर सकते हैं। उदाहरण के लिए, दशमलव अंश 1.4 सामान्य अंश 14/10 से मेल खाता है, इसलिए निर्देशांक 1.4 वाला बिंदु एक इकाई खंड के दसवें हिस्से के बराबर 14 खंडों द्वारा सकारात्मक दिशा में मूल से हटा दिया जाता है।

किसी दिए गए दशमलव अंश के अंकों में अपघटन से शुरू करके, दशमलव अंशों को एक समन्वय किरण पर चिह्नित किया जा सकता है। उदाहरण के लिए, आइए हमें निर्देशांक 16.3007 के साथ एक बिंदु बनाने की आवश्यकता है, क्योंकि 16.3007=16+0.3+0.0007, फिर हम निर्देशांक की उत्पत्ति से 16 इकाई खंडों को क्रमिक रूप से बिछाकर इस बिंदु तक पहुंच सकते हैं, 3 खंड जिनकी लंबाई दसवें के बराबर है एक इकाई का, और 7 खंड, जिनकी लंबाई एक इकाई खंड के दस हजारवें हिस्से के बराबर है।

एक निर्देशांक किरण पर दशमलव संख्याएँ बनाने की यह विधि आपको अनंत दशमलव अंश के अनुरूप बिंदु के जितना करीब चाहें उतना करीब पहुंचने की अनुमति देती है।

कभी-कभी अनंत दशमलव अंश के अनुरूप बिंदु को सटीक रूप से प्लॉट करना संभव होता है। उदाहरण के लिए, , तो यह अनंत दशमलव अंश 1.41421... निर्देशांक किरण पर एक बिंदु से मेल खाता है, जो 1 इकाई खंड की भुजा वाले वर्ग के विकर्ण की लंबाई से निर्देशांक की उत्पत्ति से दूर है।

निर्देशांक किरण पर दिए गए बिंदु के अनुरूप दशमलव अंश प्राप्त करने की विपरीत प्रक्रिया तथाकथित है किसी खंड का दशमलव माप. आइए जानें कि यह कैसे किया जाता है।

मान लीजिए कि हमारा कार्य मूल बिंदु से निर्देशांक रेखा पर दिए गए बिंदु तक पहुंचना है (या यदि हम उस तक नहीं पहुंच पाते हैं तो उस तक अनंत काल तक पहुंचना है)। एक खंड के दशमलव माप के साथ, हम क्रमिक रूप से मूल से किसी भी संख्या में इकाई खंडों को हटा सकते हैं, फिर ऐसे खंड जिनकी लंबाई एक इकाई के दसवें हिस्से के बराबर है, फिर ऐसे खंड जिनकी लंबाई एक इकाई के सौवें हिस्से के बराबर है, आदि। अलग रखी गई प्रत्येक लंबाई के खंडों की संख्या को रिकॉर्ड करके, हम निर्देशांक किरण पर दिए गए बिंदु के अनुरूप दशमलव अंश प्राप्त करते हैं।

उदाहरण के लिए, उपरोक्त चित्र में बिंदु M तक पहुंचने के लिए, आपको 1 इकाई खंड और 4 खंडों को अलग रखना होगा, जिनकी लंबाई एक इकाई के दसवें हिस्से के बराबर है। इस प्रकार, बिंदु M दशमलव भिन्न 1.4 से मेल खाता है।

यह स्पष्ट है कि निर्देशांक किरण के बिंदु, जिन तक दशमलव माप की प्रक्रिया में नहीं पहुंचा जा सकता, अनंत दशमलव भिन्नों के अनुरूप होते हैं।

ग्रंथ सूची.

• अंक शास्त्र: पाठ्यपुस्तक 5वीं कक्षा के लिए. सामान्य शिक्षा संस्थान / एन. हां. विलेंकिन, वी. आई. झोखोव, ए. एस. चेसनोकोव, एस. आई. श्वार्ट्सबर्ड। - 21वां संस्करण, मिटाया गया। - एम.: मेनेमोसिन, 2007. - 280 पीपी.: बीमार। आईएसबीएन 5-346-00699-0।
• अंक शास्त्र।छठी कक्षा: शैक्षणिक। सामान्य शिक्षा के लिए संस्थान / [एन. हां विलेनकिन और अन्य]। - 22वां संस्करण, रेव। - एम.: मेनेमोसिन, 2008. - 288 पी.: बीमार। आईएसबीएन 978-5-346-00897-2.
• बीजगणित:पाठयपुस्तक आठवीं कक्षा के लिए. सामान्य शिक्षा संस्थान / [यु. एन. मकार्यचेव, एन. जी. माइंड्युक, के. आई. नेशकोव, एस. बी. सुवोरोवा]; द्वारा संपादित एस. ए. तेल्यकोवस्की। - 16वाँ संस्करण। - एम.: शिक्षा, 2008. - 271 पी। : बीमार। - आईएसबीएन 978-5-09-019243-9।
• गुसेव वी.ए., मोर्दकोविच ए.जी.गणित (तकनीकी स्कूलों में प्रवेश करने वालों के लिए एक मैनुअल): प्रोक। भत्ता.- एम.; उच्च स्कूल, 1984.-351 पी., बीमार।

हम पहले ही कह चुके हैं कि भिन्न होते हैं साधारणऔर दशमलव. पर इस पलहमने भिन्नों का थोड़ा अध्ययन किया है। हमने सीखा कि नियमित और अनुचित भिन्न होते हैं। हमने यह भी सीखा कि सामान्य भिन्नों को घटाया, जोड़ा, घटाया, गुणा और विभाजित किया जा सकता है। और हमने यह भी सीखा कि तथाकथित मिश्रित संख्याएँ भी होती हैं, जिनमें एक पूर्णांक और एक भिन्नात्मक भाग होता है।

हमने अभी तक सामान्य भिन्नों का पूरी तरह से पता नहीं लगाया है। ऐसी कई सूक्ष्मताएं और विवरण हैं जिनके बारे में बात की जानी चाहिए, लेकिन आज हम अध्ययन शुरू करेंगे दशमलवभिन्न, चूँकि साधारण और दशमलव भिन्नों को अक्सर संयोजित करना पड़ता है। अर्थात्, समस्याओं को हल करते समय आपको दोनों प्रकार के भिन्नों का उपयोग करना होगा।

यह पाठ जटिल और भ्रमित करने वाला लग सकता है। यह बिल्कुल सामान्य है. इस प्रकार के पाठों के लिए आवश्यक है कि उनका अध्ययन किया जाए, न कि सतही तौर पर सरसरी निगाह से देखा जाए।

पाठ सामग्री

मात्राओं को भिन्नात्मक रूप में व्यक्त करना

कभी-कभी किसी चीज़ को भिन्नात्मक रूप में दिखाना सुविधाजनक होता है। उदाहरण के लिए, एक डेसीमीटर का दसवां हिस्सा इस प्रकार लिखा जाता है:

इस अभिव्यक्ति का अर्थ है कि एक डेसीमीटर को दस भागों में विभाजित किया गया था, और इन दस भागों से एक भाग लिया गया था:

जैसा कि आप चित्र में देख सकते हैं, एक डेसीमीटर का दसवां हिस्सा एक सेंटीमीटर है।

निम्नलिखित उदाहरण पर विचार करें. 6 सेमी और अन्य 3 मिमी को भिन्नात्मक रूप में सेंटीमीटर में दिखाएँ।

तो, आपको 6 सेमी और 3 मिमी को सेंटीमीटर में व्यक्त करने की आवश्यकता है, लेकिन भिन्नात्मक रूप में। हमारे पास पहले से ही 6 पूरे सेंटीमीटर हैं:

लेकिन अभी भी 3 मिलीमीटर बाकी है. इन 3 मिलीमीटर को और सेंटीमीटर में कैसे दिखाएं? अंश बचाव के लिए आते हैं। 3 मिलीमीटर एक सेंटीमीटर का तीसरा भाग है। और एक सेंटीमीटर के तीसरे भाग को सेमी लिखा जाता है

भिन्न का अर्थ है कि एक सेंटीमीटर को दस बराबर भागों में विभाजित किया गया था, और इन दस भागों से तीन भाग निकाले गए (दस में से तीन)।

परिणामस्वरूप, हमारे पास छह पूरे सेंटीमीटर और एक सेंटीमीटर का तीन दसवां हिस्सा है:

इस मामले में, 6 पूरे सेंटीमीटर की संख्या दिखाता है, और अंश आंशिक सेंटीमीटर की संख्या दिखाता है। इस भिन्न को इस प्रकार पढ़ा जाता है "छह दशमलव तीन सेंटीमीटर".

वे भिन्न जिनके हर में संख्याएँ 10, 100, 1000 हों, उन्हें हर के बिना लिखा जा सकता है। पहले पूरा भाग लिखें, और फिर भिन्नात्मक भाग का अंश लिखें। पूर्णांक भाग को भिन्नात्मक भाग के अंश से अल्पविराम द्वारा अलग किया जाता है।

उदाहरण के लिए, आइए इसे हर के बिना लिखें। ऐसा करने के लिए, आइए सबसे पहले पूरा भाग लिखें। पूर्णांक भाग संख्या 6 है। सबसे पहले हम इस संख्या को लिखते हैं:

सारा पार्ट रिकार्ड किया हुआ है। पूरा भाग लिखने के तुरंत बाद हम अल्पविराम लगाते हैं:

और अब हम भिन्नात्मक भाग का अंश लिखते हैं। मिश्रित संख्या में, भिन्नात्मक भाग का अंश संख्या 3 होता है। हम दशमलव बिंदु के बाद तीन लिखते हैं:

इस रूप में प्रदर्शित कोई भी संख्या कहलाती है दशमलव.

इसलिए, आप दशमलव अंश का उपयोग करके 6 सेमी और सेंटीमीटर में अन्य 3 मिमी दिखा सकते हैं:

6.3 सेमी

यह इस तरह दिखेगा:

वास्तव में, दशमलव सामान्य भिन्नों और मिश्रित संख्याओं के समान ही होते हैं। ऐसे भिन्नों की ख़ासियत यह है कि उनके भिन्नात्मक भाग के हर में संख्याएँ 10, 100, 1000 या 10000 होती हैं।

मिश्रित संख्या की तरह, दशमलव भिन्न में एक पूर्णांक भाग और एक भिन्नात्मक भाग होता है। उदाहरण के लिए, किसी मिश्रित संख्या में पूर्णांक भाग 6 है, और भिन्नात्मक भाग है।

दशमलव भिन्न 6.3 में, पूर्णांक भाग संख्या 6 है, और भिन्नात्मक भाग भिन्न का अंश है, अर्थात संख्या 3 है।

ऐसा भी होता है कि साधारण भिन्न जिनके हर में संख्याएँ 10, 100, 1000 बिना किसी पूर्णांक भाग के दी जाती हैं। उदाहरण के लिए, एक भिन्न पूर्ण भाग के बिना दिया जाता है। ऐसे भिन्न को दशमलव के रूप में लिखने के लिए पहले 0 लिखें, फिर अल्पविराम लगाएं और भिन्न का अंश लिखें। हर के बिना भिन्न को इस प्रकार लिखा जाएगा:

जैसे पढ़ता है "शून्य दशमलव पाँच".

मिश्रित संख्याओं को दशमलव में परिवर्तित करना

जब हम हर के बिना मिश्रित संख्याएँ लिखते हैं, तो हम उन्हें दशमलव भिन्नों में बदल देते हैं। भिन्नों को दशमलव में परिवर्तित करते समय, कुछ चीजें हैं जिन्हें आपको जानना आवश्यक है, जिनके बारे में हम अभी बात करेंगे।

पूरा भाग लिखने के बाद, भिन्नात्मक भाग के हर में शून्य की संख्या गिनना आवश्यक है, क्योंकि भिन्नात्मक भाग के शून्य की संख्या और दशमलव अंश में दशमलव बिंदु के बाद अंकों की संख्या होनी चाहिए। वही। इसका मतलब क्या है? निम्नलिखित उदाहरण पर विचार करें:

सर्वप्रथम

और आप भिन्नात्मक भाग का अंश तुरंत लिख सकते हैं और दशमलव भिन्न तैयार है, लेकिन आपको निश्चित रूप से भिन्नात्मक भाग के हर में शून्य की संख्या गिनने की आवश्यकता है।

इसलिए, हम मिश्रित संख्या के भिन्नात्मक भाग में शून्य की संख्या गिनते हैं। भिन्नात्मक भाग के हर में एक शून्य होता है। इसका मतलब यह है कि दशमलव भिन्न में दशमलव बिंदु के बाद एक अंक होगा और यह अंक मिश्रित संख्या के भिन्नात्मक भाग का अंश होगा, अर्थात संख्या 2

इस प्रकार, जब एक मिश्रित संख्या को दशमलव भिन्न में परिवर्तित किया जाता है, तो वह 3.2 हो जाती है।

यह दशमलव अंश इस प्रकार पढ़ता है:

"तीन बिंदु दो"

"दसवां" क्योंकि संख्या 10 मिश्रित संख्या के भिन्नात्मक भाग में है।

उदाहरण 2.मिश्रित संख्या को दशमलव में बदलें.

पूरा भाग लिखें और अल्पविराम लगाएं:

और आप भिन्नात्मक भाग के अंश को तुरंत लिख सकते हैं और दशमलव भिन्न 5.3 प्राप्त कर सकते हैं, लेकिन नियम कहता है कि दशमलव बिंदु के बाद उतने ही अंक होने चाहिए जितने मिश्रित संख्या के भिन्नात्मक भाग के हर में शून्य हों। और हम देखते हैं कि भिन्नात्मक भाग के हर में दो शून्य होते हैं। इसका मतलब यह है कि हमारे दशमलव अंश में दशमलव बिंदु के बाद दो अंक होने चाहिए, एक नहीं।

ऐसे मामलों में, भिन्नात्मक भाग के अंश को थोड़ा संशोधित करने की आवश्यकता है: अंश से पहले एक शून्य जोड़ें, अर्थात संख्या 3 से पहले

अब आप इस मिश्रित संख्या को दशमलव भिन्न में बदल सकते हैं। पूरा भाग लिखें और अल्पविराम लगाएं:

और भिन्नात्मक भाग का अंश लिखिए:

दशमलव भिन्न 5.03 इस प्रकार पढ़ा जाता है:

"पांच दशमलव तीन"

"सैकड़ा" क्योंकि मिश्रित संख्या के भिन्नात्मक भाग के हर में संख्या 100 होती है।

उदाहरण 3.मिश्रित संख्या को दशमलव में बदलें.

पिछले उदाहरणों से, हमने सीखा कि किसी मिश्रित संख्या को सफलतापूर्वक दशमलव में बदलने के लिए, भिन्न के अंश में अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान होनी चाहिए।

किसी मिश्रित संख्या को दशमलव अंश में बदलने से पहले, उसके भिन्नात्मक भाग को थोड़ा संशोधित करने की आवश्यकता होती है, अर्थात्, यह सुनिश्चित करने के लिए कि भिन्नात्मक भाग के अंश में अंकों की संख्या और भिन्नात्मक भाग के हर में शून्य की संख्या होती है। वही।

सबसे पहले, हम भिन्नात्मक भाग के हर में शून्य की संख्या को देखते हैं। हम देखते हैं कि तीन शून्य हैं:

हमारा कार्य भिन्नात्मक भाग के अंश में तीन अंकों को व्यवस्थित करना है। हमारे पास पहले से ही एक अंक है - यह संख्या 2 है। इसमें दो और अंक जोड़ना बाकी है। वे दो शून्य होंगे. उन्हें संख्या 2 से पहले जोड़ें। परिणामस्वरूप, हर में शून्य की संख्या और अंश में अंकों की संख्या समान होगी:

अब आप इस मिश्रित संख्या को दशमलव भिन्न में बदलना शुरू कर सकते हैं। पहले हम पूरा भाग लिखते हैं और अल्पविराम लगाते हैं:

और भिन्नात्मक भाग का अंश तुरंत लिख लें

3,002

हम देखते हैं कि दशमलव बिंदु के बाद अंकों की संख्या और मिश्रित संख्या के भिन्नात्मक भाग के हर में शून्य की संख्या समान होती है।

दशमलव भिन्न 3.002 इस प्रकार पढ़ा जाता है:

"तीन दशमलव दो हज़ारवाँ भाग"

"हज़ारवां" क्योंकि मिश्रित संख्या के भिन्नात्मक भाग के हर में संख्या 1000 होती है।

भिन्नों को दशमलव में बदलना

10, 100, 1000, या 10000 के हर वाले सामान्य भिन्नों को भी दशमलव में बदला जा सकता है। चूँकि एक साधारण भिन्न में पूर्णांक भाग नहीं होता है, पहले 0 लिखें, फिर अल्पविराम लगाएं और भिन्नात्मक भाग का अंश लिखें।

यहां भी हर में शून्य की संख्या और अंश में अंकों की संख्या समान होनी चाहिए। इसलिए आपको सावधान रहना चाहिए.

उदाहरण 1।

पूरा भाग गायब है, इसलिए पहले हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब हम हर में शून्य की संख्या देखते हैं। हम देखते हैं कि एक शून्य है। और अंश में एक अंक होता है। इसका मतलब है कि आप दशमलव बिंदु के बाद संख्या 5 लिखकर दशमलव अंश को सुरक्षित रूप से जारी रख सकते हैं

परिणामी दशमलव भिन्न 0.5 में, दशमलव बिंदु के बाद अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान होती है। इसका मतलब है कि अंश का अनुवाद सही ढंग से किया गया है।

दशमलव भिन्न 0.5 इस प्रकार पढ़ा जाता है:

"शून्य दशमलव पांच"

उदाहरण 2.भिन्न को दशमलव में बदलें.

एक पूरा हिस्सा गायब है. सबसे पहले हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब हम हर में शून्य की संख्या देखते हैं। हम देखते हैं कि दो शून्य हैं। और अंश में केवल एक अंक होता है। अंकों की संख्या और शून्य की संख्या को समान बनाने के लिए, संख्या 2 से पहले अंश में एक शून्य जोड़ें। तब भिन्न रूप ले लेगा। अब हर में शून्य की संख्या और अंश में अंकों की संख्या समान है। तो आप दशमलव अंश जारी रख सकते हैं:

परिणामी दशमलव भिन्न 0.02 में, दशमलव बिंदु के बाद अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान होती है। इसका मतलब है कि अंश का अनुवाद सही ढंग से किया गया है।

दशमलव अंश 0.02 इस प्रकार पढ़ा जाता है:

"शून्य दशमलव दो।"

उदाहरण 3.भिन्न को दशमलव में बदलें.

0 लिखें और अल्पविराम लगाएं:

अब हम भिन्न के हर में शून्य की संख्या गिनते हैं। हम देखते हैं कि पाँच शून्य हैं, और अंश में केवल एक अंक है। हर में शून्य की संख्या और अंश में अंकों की संख्या को समान बनाने के लिए, आपको संख्या 5 से पहले अंश में चार शून्य जोड़ने होंगे:

अब हर में शून्य की संख्या और अंश में अंकों की संख्या समान है। इसलिए हम दशमलव भिन्न के साथ जारी रख सकते हैं। दशमलव बिंदु के बाद भिन्न का अंश लिखें

परिणामी दशमलव भिन्न 0.00005 में, दशमलव बिंदु के बाद अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान होती है। इसका मतलब है कि अंश का अनुवाद सही ढंग से किया गया है।

दशमलव अंश 0.00005 इस प्रकार पढ़ा जाता है:

"शून्य दशमलव पाँच सौ हज़ारवां।"

अनुचित भिन्नों को दशमलव में बदलना

अनुचित भिन्न वह भिन्न होती है जिसमें अंश हर से बड़ा होता है। ऐसी अनुचित भिन्नें होती हैं जिनमें हर संख्याएँ 10, 100, 1000 या 10000 होती हैं। ऐसी भिन्नों को दशमलव में बदला जा सकता है। लेकिन दशमलव भिन्न में बदलने से पहले ऐसे भिन्नों को पूर्ण भाग में अलग करना होगा।

उदाहरण 1।

भिन्न एक अनुचित भिन्न है. ऐसे भिन्न को दशमलव भिन्न में बदलने के लिए, आपको पहले उसके पूरे भाग का चयन करना होगा। आइए याद रखें कि अनुचित भिन्नों के पूरे भाग को कैसे अलग किया जाए। यदि आप भूल गए हैं, तो हम आपको सलाह देते हैं कि आप वापस आकर इसका अध्ययन करें।

तो आइए अनुचित भिन्न में पूरे भाग को हाइलाइट करें। याद रखें कि भिन्न का अर्थ है विभाजन - में इस मामले मेंसंख्या 112 को संख्या 10 से विभाजित करना

आइए इस तस्वीर को देखें और बच्चों के निर्माण सेट की तरह एक नया मिश्रित नंबर इकट्ठा करें। संख्या 11 पूर्णांक भाग होगी, संख्या 2 भिन्नात्मक भाग का अंश होगी, और संख्या 10 भिन्नात्मक भाग का हर होगा।

हमें मिश्रित संख्या मिली. आइए इसे दशमलव भिन्न में बदलें। और हम पहले से ही जानते हैं कि ऐसी संख्याओं को दशमलव भिन्नों में कैसे परिवर्तित किया जाए। सबसे पहले, पूरा भाग लिखें और अल्पविराम लगाएं:

अब हम भिन्नात्मक भाग के हर में शून्य की संख्या गिनते हैं। हम देखते हैं कि एक शून्य है। और भिन्नात्मक भाग के अंश में एक अंक होता है। इसका मतलब यह है कि भिन्नात्मक भाग के हर में शून्य की संख्या और भिन्नात्मक भाग के अंश में अंकों की संख्या समान है। इससे हमें दशमलव बिंदु के बाद भिन्नात्मक भाग के अंश को तुरंत लिखने का अवसर मिलता है:

परिणामी दशमलव भिन्न 11.2 में, दशमलव बिंदु के बाद अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान है। इसका मतलब है कि अंश का अनुवाद सही ढंग से किया गया है।

इसका मतलब यह है कि एक अनुचित भिन्न को दशमलव में बदलने पर 11.2 हो जाता है।

दशमलव भिन्न 11.2 इस प्रकार पढ़ा जाता है:

"ग्यारह दशमलव दो।"

उदाहरण 2.अनुचित भिन्न को दशमलव में बदलें.

यह एक अनुचित भिन्न है क्योंकि अंश हर से बड़ा है। लेकिन इसे दशमलव भिन्न में बदला जा सकता है, क्योंकि हर में संख्या 100 होती है।

सबसे पहले, आइए इस भिन्न के पूर्ण भाग का चयन करें। ऐसा करने के लिए, 450 को एक कोने से 100 से विभाजित करें:

आइए एक नई मिश्रित संख्या एकत्र करें - हमें मिलता है। और हम पहले से ही जानते हैं कि मिश्रित संख्याओं को दशमलव भिन्नों में कैसे बदला जाता है।

पूरा भाग लिखें और अल्पविराम लगाएं:

अब हम भिन्नात्मक भाग के हर में शून्य की संख्या और भिन्नात्मक भाग के अंश में अंकों की संख्या की गणना करते हैं। हम देखते हैं कि हर में शून्य की संख्या और अंश में अंकों की संख्या समान है। इससे हमें दशमलव बिंदु के बाद भिन्नात्मक भाग के अंश को तुरंत लिखने का अवसर मिलता है:

परिणामी दशमलव भिन्न 4.50 में, दशमलव बिंदु के बाद अंकों की संख्या और भिन्न के हर में शून्य की संख्या समान होती है। इसका मतलब है कि अंश का अनुवाद सही ढंग से किया गया है।

इसका मतलब यह है कि एक अनुचित भिन्न को दशमलव में बदलने पर 4.50 हो जाता है।

समस्याओं को हल करते समय, यदि दशमलव भिन्न के अंत में शून्य हों, तो उन्हें ख़ारिज किया जा सकता है। आइए अपने उत्तर में शून्य भी हटा दें। तब हमें 4.5 मिलता है

यह दशमलव के बारे में दिलचस्प बातों में से एक है। यह इस तथ्य में निहित है कि किसी अंश के अंत में आने वाले शून्य इस अंश को कोई भार नहीं देते हैं। दूसरे शब्दों में, दशमलव 4.50 और 4.5 बराबर हैं। आइए उनके बीच एक समान चिह्न लगाएं:

4,50 = 4,5

सवाल उठता है कि ऐसा क्यों होता है? आख़िरकार, 4.50 और 4.5 अलग-अलग भिन्नों की तरह दिखते हैं। सारा रहस्य भिन्नों के मूल गुण में निहित है, जिसका अध्ययन हमने पहले किया था। हम यह सिद्ध करने का प्रयास करेंगे कि दशमलव भिन्न 4.50 और 4.5 बराबर क्यों हैं, लेकिन अगले विषय का अध्ययन करने के बाद, जिसे "दशमलव भिन्न को मिश्रित संख्या में बदलना" कहा जाता है।

दशमलव को मिश्रित संख्या में परिवर्तित करना

किसी भी दशमलव अंश को वापस मिश्रित संख्या में बदला जा सकता है। ऐसा करने के लिए, दशमलव भिन्नों को पढ़ने में सक्षम होना ही पर्याप्त है। उदाहरण के लिए, आइए 6.3 को मिश्रित संख्या में बदलें। 6.3 छह दशमलव तीन है. सबसे पहले हम छह पूर्णांक लिखते हैं:

और तीन दसवें के आगे:

उदाहरण 2.दशमलव 3.002 को मिश्रित संख्या में बदलें

3.002 तीन पूर्ण और दो हज़ारवां है। पहले हम तीन पूर्णांक लिखते हैं

और इसके आगे हम दो हज़ारवां लिखते हैं:

उदाहरण 3.दशमलव 4.50 को मिश्रित संख्या में बदलें

4.50 चार दशमलव पचास है। चार पूर्णांक लिखिए

और अगले पचास सौवां:

वैसे, आइए पिछले विषय से अंतिम उदाहरण याद रखें। हमने कहा कि दशमलव 4.50 और 4.5 बराबर हैं। हमने यह भी कहा कि शून्य को छोड़ा जा सकता है। आइए यह सिद्ध करने का प्रयास करें कि दशमलव 4.50 और 4.5 बराबर हैं। ऐसा करने के लिए, हम दोनों दशमलव भिन्नों को मिश्रित संख्याओं में परिवर्तित करते हैं।

जब मिश्रित संख्या में परिवर्तित किया जाता है, तो दशमलव 4.50 हो जाता है, और दशमलव 4.5 हो जाता है

हमारे पास दो मिश्रित संख्याएँ हैं और। आइए इन मिश्रित संख्याओं को अनुचित भिन्नों में बदलें:

अब हमारे पास दो भिन्न हैं और। अब भिन्न के मूल गुण को याद करने का समय आ गया है, जो कहता है कि जब आप किसी भिन्न के अंश और हर को एक ही संख्या से गुणा (या विभाजित) करते हैं, तो भिन्न का मान नहीं बदलता है।

आइए पहले भिन्न को 10 से विभाजित करें

हमें मिला, और यह दूसरा अंश है। इसका मतलब है कि दोनों एक दूसरे के बराबर हैं और समान मूल्य के बराबर हैं:

कैलकुलेटर का उपयोग करके पहले 450 को 100 से विभाजित करने का प्रयास करें, और फिर 45 को 10 से विभाजित करने का प्रयास करें। यह एक अजीब बात होगी।

दशमलव भिन्न को भिन्न में बदलना

किसी भी दशमलव भिन्न को वापस भिन्न में बदला जा सकता है। ऐसा करने के लिए, फिर से, दशमलव भिन्नों को पढ़ने में सक्षम होना ही पर्याप्त है। उदाहरण के लिए, आइए 0.3 को एक सामान्य भिन्न में बदलें। 0.3 शून्य दशमलव तीन है. सबसे पहले हम शून्य पूर्णांक लिखते हैं:

और तीन दसवें के आगे 0. शून्य को परंपरागत रूप से नहीं लिखा जाता है, इसलिए अंतिम उत्तर 0 नहीं, बल्कि बस होगा।

उदाहरण 2.दशमलव भिन्न 0.02 को भिन्न में बदलें।

0.02 शून्य दशमलव दो है. हम शून्य नहीं लिखते, इसलिए हम तुरंत दो सौवां लिख देते हैं

उदाहरण 3. 0.00005 को भिन्न में बदलें

0.00005 शून्य दशमलव पांच है. हम शून्य नहीं लिखते, इसलिए हम तुरंत पाँच सौ हज़ारवां लिख देते हैं

क्या आपको पाठ पसंद आया?
हमारे नए VKontakte समूह में शामिल हों और नए पाठों के बारे में सूचनाएं प्राप्त करना शुरू करें