Hanapin derivative ng isang trigonometriko function kailangan gamitin talahanayan ng mga derivatives, katulad ng mga derivatives 6-13.
Kapag nahanap mo pangunahing derivatives trigonometriko function Upang maiwasan ang mga karaniwang pagkakamali, dapat mong bigyang pansin ang mga sumusunod na puntos:
- sa isang function expression, ang isa sa mga termino ay madalas sine, cosine o iba pang trigonometric function hindi mula sa argumento ng function, ngunit mula sa numero (constant), samakatuwid ang derivative ng term na ito ay katumbas ng zero;
- halos palaging kailangan mong gawing simple ang expression na nakuha bilang isang resulta ng pagkita ng kaibhan, at para dito kailangan mong kumpiyansa na gumamit ng kaalaman sa mga operasyon na may mga fraction;
- Upang gawing simple ang isang expression, halos palaging kailangan mong malaman ang mga trigonometric na pagkakakilanlan, halimbawa, ang formula dobleng anggulo at ang formula para sa pagkakaisa bilang kabuuan ng mga parisukat ng sine at cosine.
Halimbawa 1. Hanapin ang derivative ng isang function
Solusyon. Sabihin nating kasama derivative ng cosine malinaw ang lahat, sasabihin ng marami na nagsisimulang mag-aral ng mga derivatives. Paano kung derivative ng sine labindalawa hinati sa pi? Sagot: isaalang-alang ito katumbas ng zero! Narito ang sine (isang function pagkatapos ng lahat!) ay isang bitag, dahil ang argumento ay hindi ang variable X o anumang iba pang variable, ngunit isang numero lamang. Ibig sabihin, ang sine ng numerong ito ay isang numero din. At ang derivative ng isang numero (constant), tulad ng alam natin mula sa talahanayan ng mga derivatives, ay katumbas ng zero. Kaya, iniiwan lamang namin ang minus na sine ng X at hanapin ang hinango nito, hindi nalilimutan ang tungkol sa tanda:
![]() .
.
Halimbawa 2. Hanapin ang derivative ng isang function
![]() .
.
Solusyon. Ang pangalawang termino ay kapareho ng kaso ng unang termino sa nakaraang halimbawa. Iyon ay, ito ay isang numero, at ang derivative ng numero ay zero. Nakita namin ang derivative ng pangalawang termino bilang derivative ng quotient:
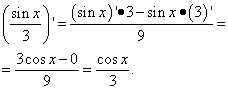
Halimbawa 3. Hanapin ang derivative ng isang function
Solusyon. Ito ay isa pang problema: dito sa unang termino ay walang arcsine o iba pang trigonometic function, ngunit mayroong x, na nangangahulugang ito ay isang function ng x. Samakatuwid, iniiba namin ito bilang isang termino sa kabuuan ng mga function:

Dito kinakailangan ang mga kasanayan sa mga operasyon na may mga fraction, ibig sabihin, sa pag-aalis ng tatlong palapag na istraktura ng isang fraction.
Halimbawa 4. Hanapin ang derivative ng isang function
![]() .
.
Solusyon. Narito ang titik na "phi" ay gumaganap ng parehong papel bilang "x" sa mga nakaraang kaso (at sa karamihan ng iba pa, ngunit hindi lahat) - ang malayang variable. Samakatuwid, kapag hinahanap natin ang derivative ng isang produkto ng mga function, hindi tayo magmamadaling ideklara ang derivative ng ugat ng "phi" na katumbas ng zero. Kaya:
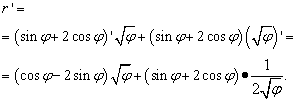
Ngunit ang solusyon ay hindi nagtatapos doon. Dahil ang mga katulad na termino ay kinokolekta sa dalawang bracket, kailangan pa rin nating baguhin (pasimplehin) ang expression. Samakatuwid, pinaparami namin ang mga bracket sa pamamagitan ng mga salik sa likod ng mga ito, at pagkatapos ay dinadala namin ang mga termino sa isang karaniwang denominator at nagsasagawa ng iba pang mga pagbabagong elementarya:

Halimbawa 5. Hanapin ang derivative ng isang function
Solusyon. Sa halimbawang ito, kakailanganin nating malaman ang katotohanan na mayroong gayong trigonometric function - ang secant - at ang mga formula nito sa pamamagitan ng cosine. Ibahin natin:

Halimbawa 6. Hanapin ang derivative ng isang function
![]() .
.
Solusyon. Sa halimbawang ito, kakailanganin nating tandaan ang double angle formula mula sa paaralan. Ngunit unahin natin ang pagkakaiba:

![]() ,
,
(ito ang double angle formula)
Ang mga derivatives ng inverse trigonometriko function at ang derivation ng kanilang mga formula ay ipinakita. Ibinibigay din ang mga expression para sa mga derivative na may mataas na pagkakasunud-sunod. Mga link sa mga pahina na may mas detalyadong paglalarawan ng derivation ng mga formula.
Una, nakukuha namin ang formula para sa derivative ng arcsine. Hayaan
y = arcsin x.
Dahil ang arcsine ay ang kabaligtaran na pag-andar ng sine, kung gayon
.
Narito ang y ay isang function ng x. Magkaiba nang may kinalaman sa variable na x:
.
Nag-a-apply kami:
.
Kaya natagpuan namin:
.
Dahil, kung gayon. Pagkatapos
.
At ang nakaraang formula ay kumukuha ng form:
. Mula rito
.
Sa eksaktong paraan na ito, maaari mong makuha ang formula para sa derivative ng arc cosine. Gayunpaman, mas madaling gumamit ng formula na may kaugnayan sa kabaligtaran na mga function ng trigonometriko:
.
Pagkatapos
.
Ang isang mas detalyadong paglalarawan ay ipinakita sa pahinang "Derivation of the derivatives of arcsine and arccosine". Doon binigay derivation ng derivatives sa dalawang paraan- tinalakay sa itaas at ayon sa formula para sa derivative ng inverse function.
Derivation ng derivatives ng arctangent at arccotangent
Sa parehong paraan makikita natin ang mga derivatives ng arctangent at arccotangent.
Hayaan
y = arctan x.
Ang Arctangent ay ang inverse function ng tangent:
.
Magkaiba nang may kinalaman sa variable na x:
.
Inilapat namin ang formula para sa derivative ng isang kumplikadong function:
.
Kaya natagpuan namin:
.
Derivative ng arc cotangent:
.
Mga derivative ng Arcsine
Hayaan
.
Natagpuan na namin ang first-order derivative ng arcsine:
.
Sa pamamagitan ng pag-iiba, makikita natin ang pangalawang-order na derivative:
;
.
Maaari rin itong isulat sa sumusunod na anyo:
.
Mula dito nakukuha natin differential equation, na nasiyahan ng arcsine derivatives ng una at pangalawang order:
.
Sa pamamagitan ng pagkakaiba-iba ng equation na ito, mahahanap natin ang mga derivatives ng mas mataas na order.
Derivative ng arcsine ng nth order
Ang derivative ng arcsine ng nth order ay may sumusunod na anyo:
,
kung saan ay isang polynomial ng degree . Ito ay tinutukoy ng mga formula:
;
.
Dito .
Natutugunan ng polynomial ang differential equation:
.
Derivative ng arccosine ng nth order
Ang mga derivatives para sa arc cosine ay nakuha mula sa mga derivatives para sa arc sine gamit ang trigonometric formula:
.
Samakatuwid, ang mga derivatives ng mga function na ito ay naiiba lamang sa sign:
.
Derivatives ng arctangent
Hayaan . Natagpuan namin ang derivative ng arc cotangent ng unang order:
.
Hatiin natin ang fraction sa pinakasimpleng anyo nito:
.
Narito ang haka-haka na yunit, .
Nag-iiba kami ng isang beses at dinadala ang fraction sa isang karaniwang denominator:
.
Ang pagpapalit , nakukuha namin ang:
.
Derivative ng arctangent ng nth order
Kaya, ang derivative ng arctangent ng nth order ay maaaring katawanin sa maraming paraan:
;
.
Derivatives ng arc cotangent
Hayaan mo na ngayon. Ilapat natin ang formula na nagkokonekta sa mga inverse trigonometric function:
.
Pagkatapos ang nth order derivative ng arc tangent ay naiiba lamang sa sign mula sa derivative ng arc tangent:
.
Ang pagpapalit , nakita namin:
.
Mga sanggunian:
N.M. Gunter, R.O. Kuzmin, Koleksyon ng mga problema sa mas mataas na matematika, "Lan", 2003.
Kapag hinango ang pinakaunang formula ng talahanayan, magpapatuloy tayo mula sa kahulugan ng derivative function sa isang punto. Dalhin natin kung saan x– anumang tunay na numero, iyon ay, x– anumang numero mula sa domain ng kahulugan ng function. Isulat natin ang limitasyon ng ratio ng increment ng function sa increment ng argument sa : ![]()
Dapat pansinin na sa ilalim ng limit sign ang expression ay nakuha, na hindi ang kawalan ng katiyakan ng zero na hinati ng zero, dahil ang numerator ay hindi naglalaman ng isang infinitesimal na halaga, ngunit tiyak na zero. Sa madaling salita, ang pagtaas ng isang pare-parehong pag-andar ay palaging zero.
kaya, derivative ng isang pare-parehong functionay katumbas ng zero sa buong domain ng kahulugan.
Derivative ng isang power function.
Derivative formula function ng kapangyarihan parang ![]() , kung saan ang exponent p– anumang tunay na numero.
, kung saan ang exponent p– anumang tunay na numero.
Patunayan muna natin ang formula para sa natural na exponent, iyon ay, para sa p = 1, 2, 3, …
Gagamitin natin ang kahulugan ng derivative. Isulat natin ang limitasyon ng ratio ng pagtaas ng isang function ng kapangyarihan sa pagtaas ng argumento: 
Upang gawing simple ang expression sa numerator, bumaling tayo sa Newton binomial formula: 
Kaya naman, 
Pinatutunayan nito ang formula para sa derivative ng isang power function para sa isang natural na exponent.
Derivative ng isang exponential function.
Ipinakita namin ang derivation ng derivative formula batay sa kahulugan:
Dumating kami sa kawalan ng katiyakan. Upang palawakin ito, ipinakilala namin ang isang bagong variable, at sa . Tapos . Sa huling paglipat, ginamit namin ang formula para sa paglipat sa isang bagong logarithmic base.
Palitan natin ang orihinal na limitasyon: 
Kung naaalala natin ang pangalawang kapansin-pansin na limitasyon, dumating tayo sa formula para sa derivative ng exponential function: 
Derivative ng isang logarithmic function.
Patunayan natin ang formula para sa derivative ng isang logarithmic function para sa lahat x mula sa domain ng kahulugan at lahat ng wastong halaga ng base a logarithm Sa pamamagitan ng kahulugan ng derivative mayroon kaming: 
Tulad ng napansin mo, sa panahon ng patunay ang mga pagbabago ay isinagawa gamit ang mga katangian ng logarithm. Pagkakapantay-pantay  ay totoo dahil sa pangalawang kahanga-hangang limitasyon.
ay totoo dahil sa pangalawang kahanga-hangang limitasyon.
Mga derivative ng trigonometriko function.
Upang makakuha ng mga formula para sa mga derivatives ng trigonometriko function, kailangan nating alalahanin ang ilang mga formula ng trigonometry, pati na rin ang unang kapansin-pansin na limitasyon.
Sa pamamagitan ng kahulugan ng derivative para sa sine function na mayroon tayo ![]() .
.
Gamitin natin ang pagkakaiba ng sinus formula: 
Ito ay nananatiling lumiko sa unang kapansin-pansing limitasyon: 
Kaya, ang derivative ng function kasalanan x meron kasi x.
Ang formula para sa derivative ng cosine ay napatunayan sa eksaktong parehong paraan. 
Samakatuwid, ang derivative ng function kasi x meron – kasalanan x.
Magkukuha tayo ng mga formula para sa talahanayan ng mga derivatives para sa tangent at cotangent gamit ang mga napatunayang panuntunan ng pagkita ng kaibhan (derivative ng isang fraction). 
Mga derivative ng hyperbolic function.
Ang mga tuntunin ng pagkita ng kaibhan at ang pormula para sa derivative ng exponential function mula sa talahanayan ng mga derivatives ay nagpapahintulot sa amin na makakuha ng mga formula para sa mga derivatives ng hyperbolic sine, cosine, tangent at cotangent. 
Derivative ng inverse function.
Upang maiwasan ang pagkalito sa panahon ng pagtatanghal, tukuyin natin sa subscript ang argumento ng function kung saan isinasagawa ang pagkita ng kaibhan, iyon ay, ito ay ang derivative ng function. f(x) Sa pamamagitan ng x.
Ngayon ay magbalangkas tayo panuntunan para sa paghahanap ng derivative ng isang inverse function.
Hayaan ang mga function y = f(x) At x = g(y) magkabaligtaran, tinukoy sa pagitan at ayon sa pagkakabanggit. Kung sa isang punto ay mayroong isang finite non-zero derivative ng function f(x), pagkatapos ay sa puntong mayroong isang finite derivative ng inverse function g(y), at ![]() . Sa ibang post
. Sa ibang post ![]() .
.
Ang panuntunang ito ay maaaring reformulated para sa alinman x mula sa pagitan , pagkatapos ay makuha namin  .
.
Suriin natin ang bisa ng mga formula na ito.
Hanapin natin ang inverse function para sa natural na logarithm ![]() (Dito y ay isang function, at x- argumento). Nang malutas ang equation na ito para sa x, nakukuha natin (dito x ay isang function, at y- ang kanyang argumento). Yan ay,
(Dito y ay isang function, at x- argumento). Nang malutas ang equation na ito para sa x, nakukuha natin (dito x ay isang function, at y- ang kanyang argumento). Yan ay, ![]() at magkabaligtaran na mga pag-andar.
at magkabaligtaran na mga pag-andar.
Mula sa talahanayan ng mga derivatives makikita natin iyon ![]() At
At ![]() .
.
Siguraduhin natin na ang mga formula para sa paghahanap ng mga derivatives ng inverse function ay magdadala sa atin sa parehong mga resulta: 
Mula sa kurso ng geometry at matematika, ang mga mag-aaral ay nasanay sa katotohanan na ang konsepto ng isang derivative ay ipinadala sa kanila sa pamamagitan ng lugar ng isang figure, mga pagkakaiba, mga limitasyon ng mga pag-andar, pati na rin ang mga limitasyon. Subukan nating tingnan ang konsepto ng derivative mula sa ibang anggulo, at tukuyin kung paano maiugnay ang mga derivative at trigonometric function.
Kaya, isaalang-alang natin ang ilang arbitrary curve na inilarawan ng abstract function na y = f(x).
Isipin natin na ang iskedyul ay isang mapa ng ruta ng turista. Ang pagtaas ng ∆x (delta x) sa figure ay isang tiyak na distansya ng landas, at ang ∆y ay ang pagbabago sa taas ng landas sa itaas ng antas ng dagat.
Pagkatapos ay lumalabas na ang ratio ∆x/∆y ay magpapakita ng pagiging kumplikado ng ruta sa bawat segment ng ruta. Sa pagkakaroon ng natutunan ang halagang ito, maaari mong kumpiyansa na sabihin kung ang pag-akyat/pagbaba ay matarik, kung kakailanganin mo ng mga kagamitan sa pag-akyat at kung ang mga turista ay nangangailangan ng isang tiyak na pisikal na pagsasanay. Ngunit ang tagapagpahiwatig na ito ay magiging wasto lamang para sa isang maliit na pagitan ∆x.
Kung ang tagapag-ayos ng paglalakbay ay kukuha ng mga halaga para sa simula at pagtatapos ng mga punto ng tugaygayan, iyon ay, ang ∆x ay katumbas ng haba ng ruta, kung gayon hindi siya makakakuha ng layunin ng data tungkol sa antas ng kahirapan ng biyahe. Samakatuwid, kinakailangan na bumuo ng isa pang graph na magpapakita ng bilis at "kalidad" ng mga pagbabago sa landas, sa madaling salita, tukuyin ang ratio ∆x/∆y para sa bawat "metro" ng ruta.
Ang graph na ito ay magiging isang visual na derivative para sa isang partikular na landas at talagang ilalarawan ang mga pagbabago nito sa bawat pagitan ng interes. Napakasimpleng i-verify ito; ang halaga ∆x/∆y ay hindi hihigit sa isang kaugalian na kinuha para sa isang tiyak na halaga ng x at y. Ilapat natin ang pagkita ng kaibhan hindi sa mga partikular na coordinate, ngunit sa function sa kabuuan:

Mga derivative at trigonometriko function
Ang mga function ng trigonometric ay hindi mapaghihiwalay na nauugnay sa mga derivatives. Ito ay mauunawaan mula sa sumusunod na pagguhit. Ang figure ng coordinate axis ay nagpapakita ng function Y = f (x) - ang asul na curve.
Ang K (x0; f (x0)) ay isang arbitrary na punto, ang x0 + ∆x ay ang pagtaas sa kahabaan ng axis ng OX, at ang f (x0 + ∆x) ay ang pagtaas sa kahabaan ng OY axis sa isang tiyak na punto L.

Gumuhit tayo ng isang tuwid na linya sa pamamagitan ng mga puntos na K at L at bumuo kanang tatsulok KLN. Kung iisipin mong ilipat ang segment na LN sa kahabaan ng graph na Y = f (x), kung gayon ang mga puntong L at N ay magiging mga halaga na K (x0; f (x0)). Tawagin natin ang puntong ito na may kondisyong simula ng graph - ang limitasyon; kung ang pag-andar ay walang katapusan, hindi bababa sa isa sa mga pagitan, ang tendensiyang ito ay magiging walang hanggan, at ang halaga ng paglilimita nito ay malapit sa 0.
Ang likas na katangian ng tendensiyang ito ay maaaring ilarawan sa pamamagitan ng isang padaplis sa napiling punto y = kx + b o sa pamamagitan ng isang graph ng derivative ng orihinal na function na dy - ang berdeng tuwid na linya.
Pero nasaan ang trigonometry dito?! Ang lahat ay napaka-simple, isaalang-alang ang tamang tatsulok na KLN. Ang halaga ng kaugalian para sa isang tiyak na punto K ay ang tangent ng anggulo α o ∠K:

Sa ganitong paraan, mailalarawan natin ang geometric na kahulugan ng derivative at ang kaugnayan nito sa mga function na trigonometriko.
Mga derivative na formula para sa trigonometriko function
Ang mga pagbabagong-anyo ng sine, cosine, tangent at cotangent kapag tinutukoy ang derivative ay dapat isaulo.

Ang huling dalawang formula ay hindi isang error, ang punto ay mayroong pagkakaiba sa pagitan ng pagtukoy sa derivative ng isang simpleng argumento at isang function sa parehong kapasidad.
Tingnan natin ang isang comparative table na may mga formula para sa mga derivatives ng sinus, cosine, tangent at cotangent:

Ang mga formula ay hinango din para sa mga derivatives ng arcsine, arccosine, arctangent at arccotangent, bagama't ang mga ito ay bihirang ginagamit:

Kapansin-pansin na ang mga formula sa itaas ay malinaw na hindi sapat upang matagumpay na malutas ang mga tipikal na gawain sa PAGGAMIT, na ipapakita kapag nilutas ang isang partikular na halimbawa ng paghahanap ng derivative ng isang trigonometriko na expression.
Mag-ehersisyo: Kinakailangang hanapin ang derivative ng function at hanapin ang halaga nito para sa π/4:

Solusyon: Upang mahanap ang y’ kinakailangan na alalahanin ang mga pangunahing formula para sa pag-convert ng orihinal na function sa isang derivative, ibig sabihin.
Paksa:"Derivative ng trigonometriko function".
Uri ng aralin– isang aral sa pagsasama-sama ng kaalaman.
Anyo ng aralin– pinagsamang aralin.
Lugar ng aralin sa sistema ng aralin para sa bahaging ito- pangkalahatang aralin.
Komprehensibong itinakda ang mga layunin:
- pang-edukasyon: alamin ang mga alituntunin ng pagkita ng kaibhan, magawang ilapat ang mga tuntunin para sa pagkalkula ng mga derivative kapag nilulutas ang mga equation at hindi pagkakapantay-pantay; pagbutihin ang paksa, kabilang ang computational, mga kasanayan at kakayahan; Mga kasanayan sa kompyuter;
- pagbuo: pagbuo ng intelektwal at lohikal na mga kasanayan at nagbibigay-malay na interes;
- pang-edukasyon: linangin ang kakayahang umangkop sa modernong kondisyon pagsasanay.
Paraan:
- reproductive at produktibo;
- praktikal at berbal;
- pansariling gawain;
- naka-program na pag-aaral, T.S.O.;
- kumbinasyon ng pangharap, pangkat at indibidwal na trabaho;
- pagkakaiba-iba ng pag-aaral;
- inductive-deductive.
Mga anyo ng kontrol:
- oral survey,
- naka-program na kontrol,
- pansariling gawain,
- mga indibidwal na gawain sa computer,
- peer review gamit ang diagnostic card ng mag-aaral.
SA PANAHON NG MGA KLASE
I. Pansamahang sandali
II. Pag-update ng kaalaman sa sanggunian
a) Pagpapahayag ng mga layunin at layunin:
- alamin ang mga alituntunin ng pagkita ng kaibhan, mailapat ang mga tuntunin para sa pagkalkula ng mga derivatives kapag nilulutas ang mga problema, equation at hindi pagkakapantay-pantay;
- pagbutihin ang paksa, kabilang ang computational, mga kasanayan at kakayahan; Mga kasanayan sa kompyuter;
- bumuo ng intelektwal at lohikal na mga kasanayan at nagbibigay-malay na interes;
- linangin ang kakayahang umangkop sa mga modernong kondisyon sa pag-aaral.
b) Pag-uulit ng materyal na pang-edukasyon
Mga panuntunan para sa pagkalkula ng mga derivatives (pag-uulit ng mga formula sa isang computer na may tunog). doc.7.
- Ano ang derivative ng sine?
- Ano ang derivative ng cosine?
- Ano ang derivative ng tangent?
- Ano ang derivative ng cotangent?
III. Oral na gawain
Hanapin ang derivative. |
|||
Pagpipilian 1. |
Opsyon 2. |
||
sa = 2X + 5. |
sa = 2X – 5. |
||
sa= 4cos X. |
sa= 3 kasalanan X. |
||
sa= tg X+ctg X. |
sa= tg X-ctg X. |
||
sa= kasalanan 3 X. |
sa= cos 4 X. |
||
Mga pagpipilian sa sagot. |
|||
– 4 kasalanan X |
– 3cos X |
||
1/cos 2 X+ 1/kasalanan 2 X |
1/cos 2 X–1/kasalanan 2 X |
1/kasalanan 2 X–1/cos 2 X |
|
– 4 kasalanan4 X |
– 3cos3 X |
||
Palitan ng mga notebook. Sa mga diagnostic card, markahan ang wastong natapos na mga gawain gamit ang isang + sign, at maling nakumpleto ang mga gawain gamit ang isang – sign.
IV. Paglutas ng mga equation gamit ang derivative
– Paano mahahanap ang mga punto kung saan ang derivative ay zero?
Upang mahanap ang mga punto kung saan ang derivative function na ito katumbas ng zero, kailangan mo:
- matukoy ang likas na katangian ng pag-andar,
- maghanap ng lugar mga kahulugan ng function,
– hanapin ang derivative ng function na ito,
– lutasin ang equation f "(x) = 0,
- Piliin ang tamang sagot.
Gawain 1.
Ibinigay: sa
= X– kasalanan x.
Hanapin: mga punto kung saan ang derivative ay zero.
Solusyon. Ang function ay tinukoy at naiba sa hanay ng lahat ng tunay na numero, dahil ang mga function ay tinukoy at naiba sa hanay ng lahat ng tunay na numero g(x) = x At t(x) = – kasalanan x.
Gamit ang mga panuntunan sa pagkita ng kaibhan, nakukuha namin f
"(x) = (x– kasalanan x)" = (x)” – (kasalanan x)" = 1 – cos x.
Kung f "(x) = 0, pagkatapos ay 1 – cos x = 0.
cos x= 1/; tanggalin natin ang irrationality sa denominator, we get cos x
= /2.
Ayon sa formula t= ± arccos a+ 2n, n Z, nakukuha natin: X= ± arccos /2 + 2n, n Z.
Sagot: x = ± /4 + 2n, n Z.
V. Paglutas ng mga equation gamit ang isang algorithm
Hanapin sa kung anong mga punto ang derivative ay naglalaho.
f(x) = kasalanan x+cos x |
f(x) = kasalanan 2 x – x |
f(x) = 2x+cos(4 x – ) |
Maaaring pumili ang mag-aaral ng alinman sa tatlong halimbawa. Ang unang halimbawa ay na-rate na " 3 ", pangalawa-" 4 ", pangatlo-" 5 " Solusyon sa mga notebook na sinusundan ng mutual checking. Isang estudyante ang nagpasya sa board. Kung ang solusyon ay lumabas na hindi tama, kailangan ng mag-aaral na bumalik sa algorithm at subukang lutasin muli.
Naka-program na kontrol.
Opsyon 1 |
Opsyon 2 |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= kasalanan 2 X– dahil 3 X. |
y= cos 2 X- kasalanan 3 X. |
|||
y= tg X–ctg( X + /4). |
y=ctg X+ tg( X – /4). |
|||
y= kasalanan 2 X. |
y= cos 2 X. |
|||
Mga pagpipilian sa sagot. |
||||
|
| ||||








