Tərif. Hansısa intervalda f(x) funksiyası təyin olunsun və x 0 bu intervalda nöqtə olsun. Əgər , onda f(x) x 0 nöqtəsində fasiləsiz deyilir.
Tərifdən belə çıxır ki, davamlılıq haqqında yalnız f(x)-in təyin olunduğu nöqtələrə münasibətdə danışmaq olar (funksiyanın həddi müəyyən edilərkən belə şərt qoyulmamışdır). Davamlı funksiyalar üçün , yəni f və lim əməliyyatları kommutativdir. Müvafiq olaraq, bir nöqtədə funksiyanın limitinin iki tərifinə davamlılığın iki tərifi verilə bilər - “ardıcıllıqların dilində” və “bərabərsizliklərin dilində” (ε-δ dilində). Bunu özünüz etməyiniz tövsiyə olunur.
Praktik istifadə üçün, artımların dilində davamlılığı müəyyən etmək bəzən daha rahatdır.
Δx=x-x 0 qiyməti arqumentin artımı adlanır, Δy=f(x)-f(x 0) isə x 0 nöqtəsindən x nöqtəsinə keçərkən funksiyanın artımıdır.
Tərif. f(x) x 0 nöqtəsində təyin olunsun. Bu nöqtədə arqumentin sonsuz kiçik artımı funksiyanın sonsuz kiçik artımına, yəni Δx→0 üçün Δy→0 uyğun gəlirsə, f(x) funksiyası x 0 nöqtəsində davamlı adlanır.

Misal 1. y=sinx funksiyasının x-in istənilən qiyməti üçün kəsilməz olduğunu sübut edin.
Həll. Qoy x 0 ixtiyari nöqtə olsun. Δx artımını verərək, x=x 0 +Δx nöqtəsini alırıq. Sonra . alırıq .
Tərif. Əgər sağda (solda) x 0 nöqtəsində y=f(x) funksiyası davamlı adlanır
.
Daxili nöqtədə davamlı funksiya həm sağ, həm də sol fasiləsiz olacaqdır. Bunun əksi də doğrudur: əgər funksiya solda və sağda bir nöqtədə davamlıdırsa, o zaman həmin nöqtədə davamlı olacaqdır. Bununla belə, funksiya yalnız bir tərəfdən davamlı ola bilər. Məsələn, üçün , , f(1)=1, buna görə də bu funksiya yalnız solda davamlıdır (bu funksiyanın qrafiki üçün yuxarıda 5.7.2-ci paraqrafa baxın).
Tərif. Funksiya bu intervalın hər nöqtəsində fasiləsizdirsə, hansısa intervalda davamlı adlanır.
Xüsusilə, əgər interval bir seqmentdirsə, onun uclarında birtərəfli davamlılıq nəzərdə tutulur.

Davamlı funksiyaların xassələri

1. Bütün elementar funksiyalar tərif dairəsində davamlıdır.
2. Müəyyən intervalda verilmiş f(x) və φ(x) bu intervalın x 0 nöqtəsində fasiləsizdirsə, bu nöqtədə funksiyalar da fasiləsiz olacaqdır.
3. Əgər X-dən x 0 nöqtəsində y=f(x), Y-dən müvafiq y 0 =f(x 0) nöqtəsində isə z=φ(y) fasiləsizdirsə, onda mürəkkəb funksiya z=φ(f(x)) x 0 nöqtəsində davamlı olacaq.

Funksiya fasilələri və onların təsnifatı

f(x) funksiyasının x 0 nöqtəsində davamlılığının əlaməti üç şərtin mövcudluğunu nəzərdə tutan bərabərlikdir:
1) f(x) x 0 nöqtəsində müəyyən edilir;
2) ;
3) .
Bu tələblərdən ən azı biri pozulubsa, x 0 funksiyanın qırılma nöqtəsi adlanır. Başqa sözlə, qırılma nöqtəsi bu funksiyanın davamlı olmadığı bir nöqtədir. Kəsmə nöqtələrinin tərifindən belə çıxır ki, funksiyanın kəsilmə nöqtələri:
a) f(x)-in davamlılıq xassəsini itirdiyi funksiyanın təyini oblastına aid olan nöqtələr,
b) funksiyanın təyin oblastının iki intervalının bitişik nöqtələri olan f(x)-in təyin oblastına aid olmayan nöqtələr.
Məsələn, funksiya üçün x=0 nöqtəsi qırılma nöqtəsidir, çünki bu nöqtədəki funksiya müəyyən edilməmişdir və funksiya f(x)-in tərif dairəsinin iki intervalına (-∞,1) və (1,∞) bitişik olan x=1 nöqtəsində kəsilməyə malikdir və mövcud deyil.

Qırılma nöqtələri üçün aşağıdakı təsnifat qəbul edilir.
1) x 0 nöqtəsində sonlular varsa Və , lakin f(x 0 +0)≠f(x 0 -0), onda x 0 adlanır birinci növ kəsilmə nöqtəsi , və adlanır funksiya atlaması .

Misal 2. Funksiyanı nəzərdən keçirin
Funksiya yalnız x=2 nöqtəsində pozula bilər (digər nöqtələrdə hər hansı çoxhədli kimi davamlıdır).
tapacağıq , . Birtərəfli hədlər sonlu, lakin bir-birinə bərabər olmadığı üçün x=2 nöqtəsində funksiya birinci növ kəsilməyə malikdir. qeyd et ki , buna görə də bu nöqtədəki funksiya sağda davamlıdır (şək. 2).
2) İkinci növ kəsilmə nöqtələri birtərəfli sərhədlərdən ən azı birinin ∞-ə bərabər olduğu və ya mövcud olmadığı nöqtələr adlanır.

Misal 3. y=2 1/ x funksiyası x=0 istisna olmaqla, x-in bütün qiymətləri üçün davamlıdır. Birtərəfli məhdudiyyətləri tapaq: , , buna görə də x=0 ikinci növ kəsilmə nöqtəsidir (şək. 3).
3) x=x 0 nöqtəsi çağırılır çıxarıla bilən qırılma nöqtəsi , əgər f(x 0 +0)=f(x 0 -0)≠f(x 0) olarsa.
Bu nöqtədə funksiyanın dəyərini təyin etməklə dəyişdirmək (yenidən təyin etmək və ya yenidən təyin etmək) kifayətdir və funksiya x 0 nöqtəsində davamlı olacaqdır.
Misal 4. Məlumdur ki , və bu hədd x-in sıfıra meyl etməsindən asılı deyil. Lakin x=0 nöqtəsindəki funksiya müəyyən edilməyib. Əgər f(0)=1 təyin etməklə funksiyanı yenidən təyin etsək, o zaman bu nöqtədə fasiləsiz olur (digər nöqtələrdə sinx və x fasiləsiz funksiyalarının hissəsi kimi davamlıdır).
Misal 5. Funksiyanın davamlılığını yoxlayın .
Həll. y=x 3 və y=2x funksiyaları hər yerdə, o cümlədən göstərilən intervallarda müəyyən edilmiş və davamlıdır. x=0 intervallarının birləşmə nöqtəsini nəzərdən keçirək:
, , . Alırıq ki, x=0 nöqtəsində funksiya davamlıdır.
Tərif. Birinci növ sonlu sayda kəsilmə nöqtələri və ya çıxarıla bilən kəsilməzlik istisna olmaqla, intervalda fasiləsiz olan funksiya bu intervalda parçalı davamlı adlanır.

Fasiləsiz funksiyaların nümunələri

Misal 1. Funksiya x=2 nöqtəsindən başqa (-∞,+∞) üzərində müəyyən edilmiş və davamlıdır. Fasilə növünü müəyyən edək. Çünki Və , onda x=2 nöqtəsində ikinci növ fasiləsizlik yaranır (şək. 6).
Misal 2. Məxrəcin sıfır olduğu x=0 istisna olmaqla, funksiya bütün x üçün müəyyən edilmiş və davamlıdır. x=0 nöqtəsində birtərəfli limitləri tapaq:
Birtərəfli hədlər sonlu və fərqlidir, ona görə də x=0 birinci növ kəsilmə nöqtəsidir (şək. 7).
Misal 3. Funksiyanın hansı nöqtələrdə və hansı növ kəsiklərə malik olduğunu müəyyənləşdirin
Bu funksiya [-2,2] üzərində müəyyən edilmişdir. [-2,0] və müvafiq olaraq, x 2 və 1/x fasiləsiz olduğundan kəsilmə yalnız intervalların qovşağında, yəni x=0 nöqtəsində baş verə bilər. olduğundan, x=0 ikinci növ kəsilmə nöqtəsidir.

Misal 4. Funksiya boşluqlarını aradan qaldırmaq mümkündürmü:
A) x=2 nöqtəsində;
b) x=2 nöqtəsində;
V) x=1 nöqtəsində?
Həll. a) misalına gəlincə, dərhal deyə bilərik ki, x=2 nöqtəsində f(x) kəsilməzliyi aradan qaldırıla bilməz, çünki bu nöqtədə sonsuz birtərəfli hədlər mövcuddur (1-ci nümunəyə bax).
b) g(x) funksiyası x=2 nöqtəsində sonlu birtərəfli limitlərə malik olsa da

(,),

lakin onlar üst-üstə düşmür, ona görə də boşluq aradan qaldırıla bilməz.
c) x=1 kəsilmə nöqtəsində φ(x) funksiyası bərabər birtərəfli sonlu hədlərə malikdir: . Buna görə də, f(1)=2 əvəzinə f(1)=1 qoymaqla x=1-də funksiyanı yenidən təyin etməklə boşluğu aradan qaldırmaq olar.

Misal 5. Dirixlet funksiyasının olduğunu göstərin

ədədi oxun hər nöqtəsində fasiləsiz.
Həll. (-∞,+∞) nöqtəsindən x 0 istənilən nöqtə olsun. Onun hər hansı bir məhəlləsində həm rasional, həm də irrasional məqamlar var. Bu o deməkdir ki, x 0-ın hər hansı qonşuluğunda funksiya 0 və 1-ə bərabər qiymətlərə malik olacaqdır. Bu halda funksiyanın x 0 nöqtəsindəki həddi nə solda, nə də sağda mövcud ola bilməz. Dirixlet funksiyası real oxun hər bir nöqtəsində ikinci növ kəsiklərə malikdir.

Misal 6. Funksiya kəsilmə nöqtələrini tapın

və onların növünü müəyyənləşdirin.
Həll. Qırılma ehtimalı olan nöqtələr x 1 =2, x 2 =5, x 3 =3 nöqtələridir.
x 1 =2 nöqtəsində f(x) ikinci növ fasiləsizliyə malikdir, çünki
.
x 2 =5 nöqtəsi davamlılıq nöqtəsidir, çünki funksiyanın bu nöqtədə və onun yaxınlığındakı qiyməti birinci deyil, ikinci xətt ilə müəyyən edilir: .
x 3 =3 nöqtəsini araşdıraq: , , buradan belə çıxır ki, x=3 birinci növ kəsilmə nöqtəsidir.

üçün müstəqil qərar.
Davamlılıq üçün funksiyaları yoxlayın və kəsilmə nöqtələrinin növünü təyin edin:
1) ; Cavab: x=-1 – çıxarıla bilən kəsilmə nöqtəsi;
2) ; Cavab: x=8 nöqtəsində ikinci növ fasiləsizlik;
3) ; Cavab: x=1-də birinci növ fasiləsizlik;
4)
Cavab: x 1 =-5 nöqtəsində çıxarıla bilən kəsilməzlik, x 2 =1 nöqtəsində ikinci növ fasiləsizlik və x 3 =0 nöqtəsində birinci növ fasiləsizlik var.
5) A rəqəmi necə seçilməlidir ki, funksiya yerinə yetirilsin

x=0-da davamlı olacaq?
Cavab: A=2.
6) A rəqəmini seçmək olarmı ki, funksiya yerinə yetirilsin

x=2-də davamlı olacaq?
Cavab: yox.

Bir nöqtədə funksiyanın davamlılığı. Funksiya y = f(x ) əvvəlcədən adlanır

x 0 nöqtəsində sarsıntı, əgər:

1) bu funksiya nöqtənin bəzi qonşuluğunda müəyyən edilir x 0;

2) həddi var f(x);

→ x 0

3) bu hədd dəyərinə bərabərdir x 0 nöqtəsində funksiyalar, yəni. limf (x )= f (x 0 ) .
		x→x0
Son şərt lim şərtinə bərabərdir		y = 0, burada x = x − x 0 – nə zaman
	x→ 0
arqumentin fırlanması, y = f (x 0 +	x )− f (x 0 ) – uyğun funksiyanın artımı
arqumentin artırılması	x, yəni. funksiyası	f(x) x 0-da davamlıdır

yalnız və yalnız bu nöqtədə arqumentin sonsuz kiçik artımı funksiyanın sonsuz kiçik artımına uyğun gələrsə.

Birtərəfli davamlılıq. y = f (x) funksiyası davamlı adlanır

solda x 0 nöqtəsində, əgər bəzi yarım intervalla (a ;x 0 ] müəyyən edilirsə

və lim f (x)= f (x 0).

x→ x0 − 0

y = f (x) funksiyası x 0 nöqtəsində düz fasiləsiz deyilir, əgər o, op-

müəyyən yarım interval üzrə paylanır [ x 0 ;a ) və limf (x )= f (x 0 ) .

x→ x0 + 0

y = f(x) funksiyası		x 0 nöqtəsində davamlıdır			sonra və yalnız o zaman
davamlı
lim f (x)= limf (x)= limf (x)= f (x 0).
x→ x0 + 0	x→ x0 − 0	x→x0

Çoxluqda funksiyanın davamlılığı. y = f (x) funksiyası çağırılır

setdə davamlı X bu çoxluğun hər nöqtəsində davamlıdırsa. Üstəlik, ədədi oxun müəyyən intervalının sonunda funksiya müəyyən edilirsə, bu nöqtədə davamlılıq sağda və ya solda davamlılıq kimi başa düşülür. Xüsusilə, y = f (x) funksiyası qeyri-ad adlanır.

seqment üzrə fasiləsiz [a; b] əgər o

1) intervalın hər nöqtəsində davamlıdır(a;b);

2) bir nöqtədə düz davamlıdır a;

3) bir nöqtədə davamlı olaraq qalır b.

Funksiya qırılma nöqtələri. y = f (x) funksiyasının təyin oblastına aid olan və ya bu oblastın sərhəd nöqtəsi olan x 0 nöqtəsi adlanır.

bu funksiyanın qırılma nöqtəsi, iff(x) həmin nöqtədə davamlı deyil.

Fasiləsizlik nöqtələri birinci və ikinci növ kəsilmə nöqtələrinə bölünür:

1) Sonlu hədlər varsa lim f (x )= f (x 0 − 0) və

x→ x0 − 0

	f (x)= f (x 0 + 0) və hər üç ədəd f (x 0 − 0), f (x 0 + 0),		f (x 0 ) bərabərdir
x→ x0 + 0
öz aralarında, sonra x 0		birinci növ kəsilmə nöqtəsi adlanır.
	Xüsusilə, əgər x 0 nöqtəsində funksiyanın sol və sağ sərhədləri		arasında bərabərdir
	özünüz, amma	bu nöqtədə funksiya dəyərinə bərabər deyil:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , onda x 0 çıxarıla bilən kəsilmə nöqtəsi adlanır.

Bu halda, f (x 0 )= A təyin etməklə, x 0 nöqtəsində funksiyanı dəyişdirə bilərsiniz

davamlı olması üçün ( funksiyanı davamlılıqla yenidən təyin edin). f (x 0 + 0)− f (x 0 − 0) fərqi deyilir bir nöqtədə funksiyanın atlanması x 0.

Çıxarılan kəsilmə nöqtəsində funksiya atlaması sıfırdır.

2) Birinci növ kəsilmə nöqtələri olmayan kəsilmə nöqtələri deyilir ikinci növ kəsilmə nöqtələri. İkinci növ kəsilmə nöqtələrində f (x 0 − 0) və f (x 0 + 0) birtərəfli hədlərindən ən azı biri mövcud deyil və ya sonsuzdur.

Bir nöqtədə davamlı funksiyaların xassələri.

		f(x)	və g (x) x 0 nöqtəsində fasiləsizdir, sonra funksiyalar
f(x)±g(x),	f(x)g(x) və	f(x)	(burada g (x)≠ 0) da x nöqtəsində davamlıdır.
		g(x)

2) u (x) funksiyası x 0 nöqtəsində fasiləsizdirsə və f (u) funksiyası davamlıdırsa.

u 0 = u (x 0) nöqtəsində, onda f (u (x)) kompleks funksiyası x 0 nöqtəsində fasiləsizdir.

3) Bütün əsas elementar funksiyalar (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) hər birində fasiləsizdir.

onların tərif sahələrinə qədər.

1)–3) xassələrindən belə nəticə çıxır ki, bütün elementar funksiyalar (sonlu sayda arifmetik əməliyyatlardan və kompozisiya əməliyyatlarından istifadə etməklə əsas elementar funksiyalardan əldə edilən funksiyalar) öz təyinat sahələrinin hər bir nöqtəsində də davamlıdır.

İntervalda davamlı funksiyaların xassələri.

1) (aralıq qiymət teoremi) f(x) funksiyası təyin olunsun

üzərində və [a;b] seqmentində davamlıdır. Sonra hər hansı C nömrəsi üçün

f (a) və f (b), (f (a) rəqəmləri arasında< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Bolzano-Koşi teoremi

[a;b] seqmentində fasiləsizdir və uclarında müxtəlif işarələrin qiymətlərini alır.

Onda ən azı bir x 0 [ a b ] nöqtəsi var ki, f (x 0 )= 0 ;

3) (1-ci Weierstrass teoremi) f (x) funksiyası təyin olunsun və

[a;b] seqmentində cırılmışdır. Sonra bu funksiya bu seqmentdə məhduddur.

4) (2 Weierstrass teoremi) f (x) funksiyası təyin olunsun və

seqmentə tələsin		[a;b] . Sonra bu funksiya [ a b ] intervalına çatır;
ən böyük		ən azı	dəyərlər, yəni.	mövcüd olmaq
x1, x2 [a; b] ,		hər hansı üçün	x [a;b] nöqtələri	ədalətli	bərabərsizliklər

f (x 1 )≤ f (x )≤ f (x 2 ) .

Misal 5.17. Davamlılığın tərifindən istifadə edərək, y = 3x 2 + 2x − 5 funksiyasının ədəd xəttinin ixtiyari x 0 nöqtəsində kəsilməz olduğunu sübut edin.

Həlli: Metod 1: X 0 ədəd oxundakı ixtiyari nöqtə olsun. Sən-

Funksiyaların cəmi və hasilinin həddi ilə bağlı teoremləri tətbiq edərək əvvəlcə f (x) funksiyasının limitini x → x 0 kimi hesablayırıq:

lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2							− 5.
x→x0	x→x0	x→x0	x→x0
Sonra x:f (x)= 3x 2 nöqtəsində funksiyanın qiymətini hesablayırıq							− 5 .
Əldə edilən nəticələri müqayisə edərək görürük				lim f (x)= f (x 0) uyğun olaraq
				x→x0

tərifi və x 0 nöqtəsində baxılan funksiyanın davamlılığını bildirir.

Metod 2: Qoy		x – 0 nöqtəsində arqumentin artımı. Gəlin yazışmaları tapaq
uyğun	artım			y = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
İndi arqumentin artımı zamanı funksiyanın artımının limitini hesablayaq
		çalışır

	y = lim (6x + 2)		x + (x )2 = (6x + 2) lim		x + (limx)2 = 0.
x→ 0	x→ 0			x→ 0	x→ 0

Beləliklə, lim y = 0, tərifinə görə davamlılıq deməkdir

x→ 0

istənilən x 0 R üçün funksiyalar.

Misal 5.18. f (x) funksiyasının kəsilmə nöqtələrini tapın və onların növünü təyin edin. IN

Çıxarılan kəsilmə halında, funksiyanı davamlılıqla təyin edin:

1) x-də f (x) = 1− x 2< 3;

x ≥ 3 olduqda 5x

2) f (x)= x 2 + 4 x + 3;

x+1

	f(x)=
		x4 (x− 2)
	f(x)= arktan
			(x − 5)

Həlli: 1) Bu funksiyanın təyin olunma sahəsi tam ədəddir

y oxu (−∞ ;+∞ ) . (−∞ ;3) ,(3;+∞ ) intervallarında funksiya fasiləsizdir. Fasilə yalnız funksiyanın analitik spesifikasiyasının dəyişdiyi x = 3 nöqtəsində mümkündür.

Göstərilən nöqtədə funksiyanın birtərəfli hədlərini tapaq:

f (3− 0)= lim (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= lim 5x = 15.

x →3 +0

Görürük ki, sol və sağ hədlər sonludur, ona görə də x = 3
qırılma I			f(x). Funksiyaya keçid
f (3+ 0)− f (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , buna görə də nöqtədə		x = 3

f(x) düz davamlıdır.

2) Funksiya nöqtədən başqa bütün say xəttində fasiləsizdir x = − 1, hansı ki, müəyyən edilməyib. Numeratoru genişləndirərək f (x) üçün ifadəni çevirək

fraksiyaları faktorlara ayırır:		f(x)=			4 x +3			(x + 1)(x + 3)	x ≠ − 1 üçün X + 3.
					x+1			x+1
x = − 1 nöqtəsində funksiyanın birtərəfli hədlərini tapaq:
	f(x)=lim	f (x )= lim(x + 3)= 2 .
x →−1−0	x →−1 +0		x →−1

Biz öyrəndik ki, tədqiq olunan nöqtədə funksiyanın sol və sağ hədləri mövcuddur, sonlu və bir-birinə bərabərdir, ona görə də x = − 1 çıxarıla bilən nöqtədir.

düz xətti y = x + 3 “deşilmiş” M nöqtəsi ilə (− 1;2) . Funksiyanın qalıcı olması üçün

fasiləsiz, f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 qoymalıyıq.

Beləliklə, f (x) -i x = − 1 nöqtəsində davamlılıqla daha da təyin edərək, təyinetmə oblastı (−∞ ;+∞ ) olan f * (x)= x + 3 funksiyasını əldə etdik.

3) Bu funksiya hər kəs üçün müəyyən edilmiş və davamlıdır x nöqtələri istisna olmaqla

x = 0,x = 2, burada kəsrin məxrəci sıfıra çevrilir.

x = 0 nöqtəsini nəzərə alın:

Kifayət qədər kiçik sıfır qonşuluğunda funksiya yalnız götürür

	mənfi qiymətlər üçün f (− 0)= lim			= −∞ = f (+0)	Bunlar. nöqtə
			(x − 2)
	x →−0
	x = 0 ikinci növ funksiyanın kəsilmə nöqtəsidir		f(x).

İndi x = 2 nöqtəsini nəzərdən keçirin:

Funksiya nəzərə alınanın soluna yaxın mənfi dəyərlər alır

	nöqtə və müsbət olanlar sağdadır, buna görə də				f (2− 0)=			= −∞,
							x4 (x− 2)
						x →2 −0
	f (2+ 0)= lim			= +∞ . Əvvəlki vəziyyətdə olduğu kimi, nöqtədə x = 2
			(x − 2)
	x →2 +0

nin nə sol, nə də sağ sonlu hədləri yoxdur, yəni. bu anda II tip qırılmaya məruz qalır.

x = 5.

f (5− 0)= lim arktan

π ,f (5+ 0)= lim arktan

x = 5

(x − 5)

(x − 5)

x →5 −0

x →5 +0

qırılma

f (5+ 0)− f (5− 0)=

π − (−

π )= π (bax. Şəkil 5.2).

Müstəqil həll ediləcək problemlər

5.174. Yalnız tərifdən istifadə edərək f (x) funksiyasının davamlılığını sübut edin

hər nöqtə x 0 R:

a) f(x) = c= const;		b) f (x)= x;
c) f (x)= x 3;		d) f (x)= 5x 2 − 4x + 1;
e) f (x)= sinx.
5.175. funksiyası olduğunu sübut edin	f(x) = x2	x ≥ 0 olduqda 1,	davam edir
		1-də x< 0
bütün nömrə xətti. Bu funksiyanın qrafikini qurun.
5.176. funksiyası olduğunu sübut edin	f(x) = x2	x ≥ 0 olduqda 1,	davamlı deyil
		0-da x< 0

x = 0 nöqtəsində, lakin bu nöqtədə düz davamlıdır. f(x) funksiyasının qrafikini çəkin.

x = nöqtəsində sarsıdıcı

Ancaq bu nöqtədə solda davamlıdır. Qrafik qurun

f(x) funksiyaları.

5.178. Qrafik funksiyalar

a) y =

x+1

b) y= x+

x+1

x+1

x+1

Bu funksiyaların kəsilmə nöqtələrində davamlılıq şərtlərindən hansı təmin edilir, hansılar təmin edilmir?

5.179. Funksiyanın kəsilmə nöqtəsini təyin edin

günah x		x ≠ 0 üçün
		x = 0-da

Davamlılıq şərtlərindən hansı bu nöqtədə təmin edilir və hansılar yerinə yetirilmir?

Tərif funksiyanın qırılma nöqtələri onların növləri isə funksiyanın davamlılığı mövzusunun davamıdır. Davamlılıq anlayışından fərqli olaraq funksiyanın qırılma nöqtələrinin mənasının əyani (qrafik) izahı da verilir. Gəlin funksiyanın kəsilmə nöqtələrini tapmağı və onların növlərini təyin etməyi öyrənək. Bizimkilər isə bu işdə bizə kömək edəcəklər sadiq dostlar- sol və sağ həddlər, ümumiyyətlə birtərəfli limitlər adlanır. Kiminsə birtərəfli məhdudiyyətlərdən qorxusu varsa, biz onu tezliklə aradan qaldıracağıq.

Qrafikdə bir-biri ilə əlaqəsi olmayan nöqtələrə deyilir funksiyanın qırılma nöqtələri . Aşağıdakı şəkildə x=2 - - nöqtəsində kəsilməyə məruz qalan belə funksiyanın qrafiki.

Yuxarıdakıların ümumiləşdirilməsi aşağıdakı tərifdir. Funksiya bir nöqtədə davamlı deyilsə, bu nöqtədə kəsikliyə malikdir və nöqtənin özü adlanır. qırılma nöqtəsi . Çatışmazlıqlar birinci və ikinci növdür .

Müəyyən etmək üçün qırılma nöqtələrinin növləri (xarakteri). funksiyaları inamla tapmaq lazımdır məhdudiyyətlər, buna görə də müvafiq dərsi yeni pəncərədə açmaq yaxşı fikirdir. Ancaq kəsilmə nöqtələri ilə əlaqədar olaraq, bizdə yeni və vacib bir şey var - birtərəfli (sol və sağ) məhdudiyyətlər. Ümumiyyətlə, onlar yazılır (sağ hədd) və (sol hədd). Ümumiyyətlə limit vəziyyətində olduğu kimi, funksiyanın limitini tapmaq üçün funksiyanın ifadəsində X-i X-in meyl etdiyi şeylə əvəz etmək lazımdır. Ancaq, bəlkə də, soruşursunuz ki, sağ və sol hədlər necə fərqlənəcək, əgər sağda X-ə bir şey əlavə olunarsa, lakin bu, sıfırdır və solda bir şey X-dən çıxarılırsa, lakin bu bir şey - həm də sıfır? Və haqlı olacaqsan. Əksər hallarda.

Lakin funksiyanın kəsilmə nöqtələrinin axtarışı və onların növünün müəyyən edilməsi praktikasında sağ və sol hədlərin bərabər olmadığı iki tipik hal var:

• funksiyada x-in aid olduğu say xəttinin hissəsindən asılı olaraq iki və ya daha çox ifadə var (bu ifadələr adətən sonra əyri mötərizədə yazılır. f(x)= );
• X-in meyl etdiyini əvəz etmək nəticəsində məxrəcində ya üstəgəl sıfır (+0) və ya mənfi sıfır (-0) qalan kəsr alırıq və buna görə də belə bir kəsr ya üstəgəl sonsuzluq, ya da mənfi sonsuzluq deməkdir və bunlar tamamilə fərqli şeylər.

Birinci növ kəsilmə nöqtələri

Birinci növ qırılma nöqtəsi: funksiyanın həm sonlu (yəni sonsuzluğa bərabər olmayan) sol həddi, həm də sonlu sağ həddi var, lakin funksiya nöqtədə müəyyən edilməyib və ya sol və sağ hədlər fərqlidir (bərabər deyil).

Birinci növ çıxarıla bilən kəsilmə nöqtəsi. Sol və sağ sərhədlər bərabərdir. Bu halda, bir nöqtədə funksiyanı əlavə olaraq təyin etmək mümkündür. Bir nöqtədə funksiyanı təyin etmək, sadə desək, sol və sağ sərhədlərin bir-birinə bərabər olduğu nöqtələrin əlaqəsini təmin etmək deməkdir. Bu halda, əlaqə funksiyanın dəyərinin tapılmalı olduğu yalnız bir nöqtəni təmsil etməlidir.

Misal 1. Funksiyanın qırılma nöqtəsini və kəsilmə nöqtəsinin tipini (xarakterini) təyin edin.

İkinci növ kəsilmə nöqtələri

İkinci növ qırılma nöqtəsi: hüdudlardan ən azı birinin (sol və ya sağ) sonsuz (sonsuzluğa bərabər) olduğu nöqtə.

Misal 3.

Həll. Gücün ifadəsindən e nöqtədə funksiyanın müəyyən edilmədiyi aydındır. Bu nöqtədə funksiyanın sol və sağ hədlərini tapaq:

Sərhədlərdən biri sonsuzluğa bərabərdir, ona görə də nöqtə ikinci növ kəsilmə nöqtəsidir. Qırılma nöqtəsi olan funksiyanın qrafiki nümunənin altındadır.

Funksiyanın kəsilmə nöqtələrinin tapılması ya müstəqil tapşırıq, ya da onun bir hissəsi ola bilər Tam funksiyalı tədqiqat və qrafika .

Misal 4. Funksiyanın qırılma nöqtəsini və funksiya üçün kəsilmə nöqtəsinin tipini (xarakterini) təyin edin

Həll. 2-də güc ifadəsindən aydın olur ki, funksiya nöqtədə təyin olunmayıb. Bu nöqtədə funksiyanın sol və sağ hədlərini tapaq.

Çıxarılan boşluq.

Tərif. Nöqtə a funksiyanın çıxarıla bilən kəsilmə nöqtəsi adlanır y=f(x), funksiyanın limiti olarsa f(x) bu nöqtədə var, amma nöqtədə a funksiyası f(x) ya müəyyən edilməyib, ya da özəl məna daşıyır f(a), limitdən fərqlidir f(x) Bu nöqtədə.

Misal. Məsələn, funksiya

nöqtəsində var x=0 təmir edilə bilən boşluq. Həqiqətən, nöqtədə bu funksiyanın məhdudlaşdırıcı dəyəri x=0 1-ə bərabərdir. Qismən qiymət 2-yə bərabərdir.

Əgər funksiyası f(x) nöqtəsində var açıxarıla bilən boşluq, o zaman bu boşluq funksiyanın dəyərindən başqa nöqtələrdə dəyişdirilmədən aradan qaldırıla bilər a. Bunun üçün funksiyanın qiymətini nöqtəyə qoymaq kifayətdir a bu nöqtədə onun limit dəyərinə bərabərdir. Beləliklə, yuxarıda nəzərdən keçirilən nümunədə qoymaq kifayətdir f(0)=1 daha sonra , yəni. funksiyası f(x) nöqtəsində davamlı olacaq x=0.

Birinci növ pozuntu.

Tərif. Nöqtə a bu nöqtədə funksiya varsa, birinci növ kəsilmə nöqtəsi adlanır f(x) sonlu, lakin qeyri-bərabər sağ və sol sərhədlərə malikdir

Bir neçə misal verək.

Misal. Funksiya y=sgn x nöqtəsində var x=0 birinci növ qırılma. Doğrudan da, bu həddlər bir-birinə bərabər deyil.

Misal. Funksiya , nöqtədən başqa hər yerdə müəyyən edilir x=1, nöqtəsində var x=1 birinci növ qırılma. Doğrudan da, .

İkinci növ pozuntu.

Tərif. Nöqtə a bu nöqtədə funksiya varsa, ikinci növ kəsilmə nöqtəsi adlanır f(x) birtərəfli hədlərdən ən azı birinə malik deyilsə və ya birtərəfli hədlərdən ən azı biri sonsuzdursa.

Misal. Funksiya f(x)=tan x, aydındır ki, hər nöqtədə ikinci növ fasiləsizliyə malikdir x k =π/2+π k, k=0, ± 1, ± 2,…, çünki hər belə nöqtədə

Misal. Funksiya nöqtədə ikinci növ fasiləsizliyə malikdir x=0, çünki bu nöqtədə onun nə sağ, nə də sol sərhədləri var.

Seqmentdə funksiyanın davamlılığı

Tərif. Funksiya intervalda müəyyən edilmişdir və onun hər bir nöqtəsində fasiləsiz olaraq bu seqmentdə davamlı deyilir.

Üstəlik, nöqtədə davamlılıq altında a sağda davamlılıq, bir nöqtədə isə davamlılıq kimi başa düşülür b- solda davamlılıq.

Funksiyasını deyəcəyik y=f(x), setdə müəyyən edilmişdir (x) onun üzərində yuxarı (aşağı) kənarına çatır , əgər belə bir nöqtə varsa x 0 ∈(x), Nə f(x 0)=β (f(x 0)=α).

[Weierstrass] Teoremi. İntervalda davamlı olan hər bir funksiya məhduddur və onun yuxarı sərhədinə və onun üzərindəki aşağı sərhədinə çatır.

Teorem [Bolzano-Cauchy]. Əgər funksiyası y=f(x) seqmentdə davamlıdır Və f(a)=A, f(b)=B, sonra hər hansı biri üçün C, arasında bağlandı A Və B, belə bir məqam var ξ∈ , Nə f(ξ)=C.

Başqa sözlə desək, intervalda fasiləsiz olan funksiya hər hansı iki qiymət alaraq onların arasında yerləşən istənilən qiyməti də alır.

Nəticə. Əgər funksiya seqmentdə davamlıdırsa və onun uclarında müxtəlif işarələrin qiymətlərini alırsa, bu seqmentdə funksiyanın yox olduğu ən azı bir nöqtə var.

Nəticə. Qoy funksiya olsun y=f(x) seqmentdə davamlıdır Və , . Sonra funksiya f(x) seqmentdən bütün dəyərləri götürür və yalnız bu dəyərlər.

Beləliklə, müəyyən bir seqmentdə verilmiş və davamlı olan funksiyanın bütün dəyərlərinin çoxluğu da bir seqmentdir.

Funksiyanın davamlılığı. Qırılma nöqtələri.

Öküz gedir, yırğalanır, ah-nalə çəkir:
- Oh, lövhə tükənir, indi yıxılacağam!

Bu dərsdə biz funksiyanın davamlılığı anlayışını, kəsilmə nöqtələrinin təsnifatını və ümumi praktiki problemi araşdıracağıq. funksiyaların davamlılığının tədqiqi. Mövzunun adından çoxları intuitiv olaraq nəyin müzakirə olunacağını təxmin edir və materialın olduqca sadə olduğunu düşünür. Bu doğrudur. Ancaq ən çox laqeydliyə və onların həllinə səthi yanaşmaya görə cəzalandırılan sadə vəzifələrdir. Buna görə də, məqaləni çox diqqətlə öyrənməyi və bütün incəlikləri və texnikaları tutmağı məsləhət görürəm.

Nəyi bilmək və bacarmaq lazımdır?Çox deyil. Dərsi yaxşı öyrənmək üçün onun nə olduğunu başa düşmək lazımdır funksiyanın limiti. ilə oxucular aşağı səviyyə məqaləni başa düşmək üçün hazırlıq kifayətdir Funksiya məhdudiyyətləri. Həll nümunələri və baxmaq həndəsi məna təlimatda məhdudiyyət Elementar funksiyaların qrafikləri və xassələri. Bununla da tanış olmaq məsləhətdir qrafiklərin həndəsi çevrilmələri, çünki təcrübə əksər hallarda rəsm çəkməyi əhatə edir. Perspektivlər hər kəs üçün nikbindir və hətta tam bir çaydan da yaxın və ya iki saat ərzində öz başına işin öhdəsindən gələ biləcək!

Funksiyanın davamlılığı. Kəsmə nöqtələri və onların təsnifatı

Funksiyanın davamlılığı anlayışı

Bütün say xəttində fasiləsiz olan bəzi funksiyaları nəzərdən keçirək:

Və ya daha qısa desək, funksiyamız davamlıdır (həqiqi ədədlər çoxluğu).

Davamlılığın “filist” meyarı nədir? Aydındır ki, cədvəl davamlı funksiya qələmi kağızdan qaldırmadan çəkmək olar.

Bu vəziyyətdə iki sadə anlayışı aydın şəkildə ayırmaq lazımdır: funksiyanın domeni Və funksiyanın davamlılığı. IN ümumi hal eyni şey deyil. Misal üçün:

Bu funksiya bütün say xəttində müəyyən edilir, yəni hər kəs“X” mənasının öz “y” mənası var. Xüsusilə, əgər , onda . Qeyd edək ki, digər nöqtədə durğu işarəsi qoyulur, çünki funksiyanın tərifinə görə arqumentin dəyəri uyğun olmalıdır yeganə şey funksiya dəyəri. Beləliklə, domen funksiyamız: .

Lakin bu funksiya davamlı deyil! Bu nöqtədə onun əziyyət çəkdiyi aydındır boşluq. Termin həm də olduqca başa düşülən və vizualdır, burada hər halda, qələmi kağızdan qoparmaq lazımdır; Bir az sonra kəsilmə nöqtələrinin təsnifatına baxacağıq.

Bir nöqtədə və intervalda funksiyanın davamlılığı

Müəyyən bir riyazi məsələdə bir nöqtədə funksiyanın davamlılığından, intervalda funksiyanın davamlılığından, yarım intervaldan və ya seqmentdəki funksiyanın davamlılığından danışmaq olar. Yəni, "sadəcə davamlılıq" yoxdur– funksiya HƏR YERDƏ davamlı ola bilər. Və hər şeyin əsas "tikinti bloku"dur funksiyanın davamlılığı nöqtədə .

Nəzəriyyə riyazi analiz“delta” və “epsilon” məhəllələrindən istifadə edərək bir nöqtədə funksiyanın davamlılığının tərifini verir, lakin praktikada daha çox diqqət yetirəcəyimiz başqa bir tərif istifadə olunur.

Əvvəlcə xatırlayaq birtərəfli məhdudiyyətlər ilk dərsdə həyatımıza girənlər funksiya qrafikləri haqqında. Gündəlik vəziyyəti nəzərdən keçirin:

Oxa nöqtəyə yaxınlaşsaq sol(qırmızı ox), sonra "oyunların" müvafiq dəyərləri ox boyunca nöqtəyə (qırmızı ox) gedəcəkdir. Riyazi olaraq, bu fakt istifadə edərək müəyyən edilir sol həddi:

Girişə diqqət yetirin ("x solda ka'ya meyllidir" oxuyur). "Əlavə" "mənfi sıfır" simvollaşdırır , mahiyyətcə bu o deməkdir ki, biz rəqəmə sol tərəfdən yaxınlaşırıq.

Eynilə, əgər “ka” nöqtəsinə yaxınlaşsanız sağda(mavi ox), sonra "oyunlar" eyni dəyərə gələcək, lakin yaşıl ox boyunca və sağ əl həddi aşağıdakı kimi formatlaşdırılacaq:

"Əlavə" simvollaşdırır , və girişdə deyilir: "x sağda ka-ya meyl edir."

Birtərəfli limitlər sonlu və bərabərdirsə(bizim vəziyyətimizdə olduğu kimi): , onda ÜMUMİ limitin olduğunu deyəcəyik. Çox sadədir, ümumi hədd bizim “adi”mizdir. funksiyanın limiti, sonlu ədədə bərabərdir.

Qeyd edək ki, əgər funksiya (punktur qara nöqtə qrafik filialında), onda yuxarıdakı hesablamalar qüvvədə qalır. Artıq bir neçə dəfə, xüsusən də məqalədə qeyd edildiyi kimi sonsuz kiçik funksiyalar haqqında, ifadələr "x" deməkdir sonsuz yaxın ikən nöqtəyə yaxınlaşır FƏRQİ YOXDUR, funksiyanın özünün verilmiş nöqtədə müəyyən edilib-edilməməsi. Yaxşı nümunə funksiya təhlil edildikdə növbəti paraqrafda görünəcək.

Tərif: verilmiş nöqtədə funksiyanın həddi həmin nöqtədəki funksiyanın qiymətinə bərabər olarsa, funksiya kəsilməzdir: .

Tərif ətraflı şəkildə verilmişdir aşağıdakı şərtlər:

1) Funksiya nöqtədə müəyyən edilməlidir, yəni qiymət mövcud olmalıdır.

2) Funksiyanın ümumi həddi olmalıdır. Yuxarıda qeyd edildiyi kimi, bu, birtərəfli məhdudiyyətlərin mövcudluğunu və bərabərliyini nəzərdə tutur: .

3) Verilmiş nöqtədə funksiyanın həddi bu nöqtədəki funksiyanın qiymətinə bərabər olmalıdır: .

Əgər pozulubsa ən azı birüç şərtdən, onda funksiya nöqtədə davamlılıq xassəsini itirir.

Funksiyanın interval üzərində davamlılığı dahiyanə və çox sadə şəkildə tərtib edilmişdir: funksiya verilmiş intervalın hər bir nöqtəsində davamlıdırsa, intervalda davamlıdır.

Xüsusilə, bir çox funksiyalar sonsuz intervalda, yəni həqiqi ədədlər çoxluğunda fasiləsizdir. Bu xətti funksiya, polinomlar, eksponensial, sinus, kosinus və s. Və ümumiyyətlə, hər hansı elementar funksiyaüzərində davamlıdır tərif sahəsi məsələn, loqarifmik funksiya intervalında davamlıdır. Mən ümid edirəm bu dəqiqəəsas funksiyaların qrafiklərinin necə göründüyü barədə kifayət qədər yaxşı təsəvvürünüz var. Daha çox ətraflı məlumat onların davamlılığını öyrənmək olar mehriban insan Fichtengolts soyadı ilə.

Bir seqmentdə və yarım intervallarda funksiyanın davamlılığı ilə hər şey çətin deyil, lakin bu barədə sinifdə danışmaq daha məqsədəuyğundur. seqmentdə funksiyanın minimum və maksimum qiymətlərinin tapılması haqqında, amma hələlik bundan narahat olmayaq.

Qırılma nöqtələrinin təsnifatı

Funksiyaların füsunkar həyatı hər cür xüsusi məqamlarla zəngindir və qırılma nöqtələri onların tərcümeyi-halının səhifələrindən yalnız biridir.

Qeyd : hər halda, elementar bir məqam üzərində dayanacağam: qırılma nöqtəsi həmişədir tək nöqtə– “ard-arda bir neçə qırılma nöqtəsi” yoxdur, yəni “fasilə intervalı” deyə bir şey yoxdur.

Bu nöqtələr öz növbəsində ikiyə bölünür böyük qruplar: birinci növ qırılmalar Və ikinci növ qırılmalar. Hər bir boşluq növü öz xüsusiyyətlərinə malikdir xüsusiyyətləri indi baxacağımız:

Birinci növ kəsilmə nöqtəsi

Bir nöqtədə davamlılıq şərti pozulursa və birtərəfli məhdudiyyətlər sonlu , sonra çağırılır birinci növ kəsilmə nöqtəsi.

Ən optimist hadisə ilə başlayaq. Dərsin orijinal ideyasına görə, mən nəzəriyyəni “in ümumi görünüş”, lakin materialın reallığını nümayiş etdirmək üçün konkret personajlarla seçim üzərində qərar verdim.

Əbədi məşəl fonunda yeni evlənənlərin fotoşəkili kimi kədərlidir, lakin aşağıdakı çəkiliş ümumiyyətlə qəbul edilir. Rəsmdə funksiyanın qrafikini təsvir edək:


Bu funksiya nöqtədən başqa bütün say xəttində davamlıdır. Və əslində məxrəc sıfıra bərabər ola bilməz. Halbuki hədd mənasına uyğun olaraq, edə bilərik sonsuz yaxın"sıfır"a həm soldan, həm də sağdan yaxınlaşın, yəni birtərəfli məhdudiyyətlər mövcuddur və açıq şəkildə üst-üstə düşür:
(2 nömrəli davamlılıq şərti təmin edilir).

Lakin funksiya nöqtədə müəyyən edilməyib, ona görə də 1 nömrəli davamlılıq şərti pozulur və funksiya bu nöqtədə kəsilməyə məruz qalır.

Bu tip fasilə (mövcud ümumi hədd) adlandırılır təmir edilə bilən boşluq. Niyə çıxarıla bilər? Çünki funksiya edə bilər yenidən müəyyən etmək qırılma nöqtəsində:

Qəribə görünür? Ola bilər. Ancaq belə bir funksiya qeydi heç bir şeyə zidd deyil! İndi boşluq bağlandı və hamı xoşbəxtdir:


Rəsmi yoxlama aparaq:

2) - ümumi məhdudiyyət var;
3)

Beləliklə, hər üç şərt yerinə yetirilir və bir nöqtədə funksiyanın davamlılığının tərifi ilə funksiya bir nöqtədə davamlıdır.

Bununla belə, matan nifrətçiləri funksiyanı pis şəkildə təyin edə bilər, məsələn :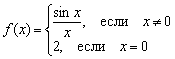


Maraqlıdır ki, burada ilk iki davamlılıq şərti təmin edilir:
1) – funksiya verilmiş nöqtədə müəyyən edilir;
2) - Ümumi məhdudiyyət var.

Amma üçüncü sərhəd keçilməmişdir: , yəni nöqtədə funksiyanın həddi bərabər deyil verilmiş nöqtədə verilmiş funksiyanın qiyməti.

Beləliklə, bir nöqtədə funksiya kəsilməyə məruz qalır.

İkinci, daha kədərli hal adlanır birinci növ qırılma atlama ilə. Kədər isə birtərəfli məhdudiyyətlərlə oyanır sonlu və fərqlidir. Bir nümunə dərsin ikinci rəsmində göstərilmişdir. Belə bir boşluq adətən zaman baş verir hissə-hissə müəyyən edilmiş funksiyalar, artıq məqalədə qeyd edilmişdir qrafik çevrilmələri haqqında.

Parça-parça funksiyasını nəzərdən keçirin və biz onun rəsmini tamamlayacağıq. Qrafiki necə qurmaq olar? Çox sadə. Yarım intervalda parabolanın bir parçasını çəkirik ( yaşıl rəng), intervalda – düz xətt seqmenti (qırmızı) və yarım intervalda – düz xətt ( Mavi rəng).

Üstəlik, bərabərsizlik səbəbiylə dəyər müəyyən edilir kvadrat funksiya(yaşıl nöqtə) və bərabərsizlik səbəbiylə , dəyəri təyin edilir xətti funksiya(mavi nöqtə):

Ən çətin vəziyyətdə, qrafikin hər bir parçasının nöqtə-nöqtəli qurulmasına müraciət etməlisiniz (birinciyə bax). funksiyaların qrafikləri haqqında dərs).

İndi bizi yalnız məqam maraqlandıracaq. Davamlılıq üçün onu yoxlayaq:

2) Birtərəfli limitləri hesablayaq.

Solda qırmızı xətt seqmentimiz var, buna görə də sol tərəfdəki limit:

Sağda mavi düz xətt və sağ tərəfdə sərhəd var:

Nəticədə aldıq sonlu ədədlər, və onlar bərabər deyil. Çünki birtərəfli məhdudiyyətlər sonlu və fərqlidir: , onda bizim funksiyamız dözür sıçrayışla birinci növ fasiləsizlik.

Məntiqlidir ki, boşluğu aradan qaldırmaq mümkün deyil - funksiya həqiqətən əvvəlki nümunədə olduğu kimi daha da müəyyən edilə və "bir-birinə yapışdırıla bilməz".

İkinci növ kəsilmə nöqtələri

Adətən, bütün digər qırılma halları ağıllı şəkildə bu kateqoriyaya təsnif edilir. Hər şeyi sadalamayacağam, çünki praktikada problemlərin 99% -ində qarşılaşacaqsınız sonsuz boşluq– solaxay və ya sağ əlli olduqda və daha tez-tez hər iki hədd sonsuzdur.

Və təbii ki, ən bariz şəkil sıfır nöqtəsindəki hiperboladır. Burada hər iki birtərəfli məhdudiyyətlər sonsuzdur: , buna görə də funksiya nöqtədə ikinci növ fasiləsizliyə məruz qalır.

Mən məqalələrimi mümkün qədər müxtəlif məzmunla doldurmağa çalışıram, ona görə də hələ rast gəlinməyən funksiyanın qrafikinə baxaq:

standart sxemə görə:

1) Məxrəc sıfıra getdiyi üçün bu nöqtədə funksiya müəyyən edilməyib.

Əlbəttə ki, biz dərhal belə nəticəyə gələ bilərik ki, funksiya nöqtədə kəsilməyə məruz qalır, lakin çox vaxt şərt tərəfindən tələb olunan kəsilmənin xarakterini təsnif etmək yaxşı olardı. Bunun üçün:

Nəzərinizə çatdırım ki, qeyd etməklə biz nəzərdə tuturuq sonsuz kiçik mənfi rəqəm , və girişin altında - sonsuz kiçik müsbət ədəd.

Birtərəfli məhdudiyyətlər sonsuzdur, yəni funksiya nöqtədə 2-ci növ fasiləsizliyə məruz qalır. y oxudur şaquli asimptot qrafik üçün.

Hər iki birtərəfli limitlərin mövcud olması qeyri-adi deyil, lakin onlardan yalnız biri sonsuzdur, məsələn:

Bu funksiyanın qrafikidir.

Davamlılıq üçün nöqtəni araşdırırıq:

1) Bu nöqtədə funksiya müəyyən edilməyib.

2) Birtərəfli limitləri hesablayaq:

Mühazirənin son iki nümunəsində bu cür birtərəfli hədlərin hesablanması üsulu haqqında danışacağıq, baxmayaraq ki, bir çox oxucu artıq hər şeyi görmüş və təxmin etmişdir.

Sol əl həddi sonludur və sıfıra bərabərdir (biz “nöqtənin özünə getmirik”), lakin sağ əl həddi sonsuzdur və qrafikin narıncı budağı sonsuz olaraq ona yaxınlaşır. şaquli asimptot, tənliklə verilmişdir (qara nöqtəli xətt).

Beləliklə, funksiya əziyyət çəkir ikinci növ fasiləsizlik nöqtədə.

1-ci növ fasiləsizliyə gəldikdə, funksiya kəsilmə nöqtəsinin özündə müəyyən edilə bilər. Məsələn, hissə-hissə funksiyası üçün Koordinatların başlanğıcına qara qalın nöqtə qoymaqdan çekinmeyin. Sağda hiperbolanın bir qolu, sağ tərəf isə sonsuzdur. Düşünürəm ki, demək olar ki, hər kəsin bu qrafikin necə göründüyü barədə bir fikri var.

Hər kəsin gözlədiyi şey:

Davamlılıq üçün funksiyanı necə yoxlamaq olar?

Bir nöqtədə davamlılıq funksiyasının tədqiqi üç fasiləsizliyin yoxlanılmasından ibarət olan artıq qurulmuş müntəzəm sxemə uyğun olaraq həyata keçirilir:

Misal 1

Funksiyanı araşdırın

Həll:

1) Əhatə dairəsinin yeganə nöqtəsi funksiyanın müəyyən edilmədiyi yerdir.

2) Birtərəfli limitləri hesablayaq:

Birtərəfli məhdudiyyətlər sonlu və bərabərdir.

Beləliklə, bu nöqtədə funksiya çıxarıla bilən fasilədən əziyyət çəkir.

Bu funksiyanın qrafiki necə görünür?

sadələşdirmək istərdim , və adi parabola alınmış kimi görünür. AMMA orijinal funksiya nöqtəsində müəyyən edilməyib, ona görə də aşağıdakı bənd tələb olunur:

Gəlin rəsm çəkək:

Cavab verin: funksiya çıxarıla bilən kəsilməyə məruz qaldığı nöqtədən başqa bütün say xəttində davamlıdır.

Funksiya daha yaxşı və ya o qədər də yaxşı olmayan şəkildə müəyyən edilə bilər, lakin şərtə görə bu tələb olunmur.

Siz deyirsiniz ki, bu çox uzaq bir nümunədir? Dəyməz. Bu, praktikada onlarla dəfə baş verib. Saytın demək olar ki, bütün tapşırıqları real müstəqil iş və testlərdən irəli gəlir.

Sevimli modullarımızdan xilas olaq:

Misal 2

Funksiyanı araşdırın davamlılıq üçün. Funksiya kəsiklərinin xarakterini, əgər varsa, müəyyən edin. Rəsmi icra edin.

Həll: Nədənsə tələbələr qorxur və modul ilə funksiyaları sevmirlər, baxmayaraq ki, onlar haqqında mürəkkəb bir şey yoxdur. Artıq dərsdə belə şeylərə bir az toxunmuşuq. Qrafiklərin həndəsi çevrilmələri. Modul mənfi olmadığı üçün aşağıdakı kimi genişləndirilir: , burada “alfa” bəzi ifadədir. IN bu halda, və funksiyamız hissə-hissə yazılmalıdır: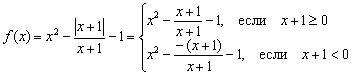

Lakin hər iki hissənin kəsirləri ilə azaldılmalıdır. Əvvəlki nümunədə olduğu kimi azalma nəticəsiz baş verməyəcək. Məxrəc sıfıra getdiyi üçün orijinal funksiya nöqtədə müəyyən edilmir. Beləliklə, sistem əlavə olaraq şərti təyin etməli və ilk bərabərsizliyi sərtləşdirməlidir:

İndi ÇOX haqqında FAYDALI qəbul həllər: qaralama üzərində tapşırığı tamamlamazdan əvvəl rəsm çəkmək (şərtlərin tələb edib-etməməsindən asılı olmayaraq) sərfəlidir. Bu, birincisi, davamlılıq nöqtələrini və kəsilmə nöqtələrini dərhal görməyə kömək edəcək və ikincisi, birtərəfli məhdudiyyətlər taparkən sizi səhvlərdən 100% qoruyacaq.

Gəlin rəsm çəkək. Hesablamalarımıza uyğun olaraq, nöqtənin solunda parabolanın bir parçasını (mavi rəng), sağda isə parabolanın bir parçasını (qırmızı rəng) çəkmək lazımdır, halbuki funksiya müəyyən edilməmişdir. özünə işarə edir:

Əgər şübhəniz varsa, bir neçə x dəyəri götürün və onları funksiyaya qoşun (modulun mümkün mənfi işarəni məhv etdiyini xatırlayaraq) və qrafiki yoxlayın.

Davamlılıq funksiyasını analitik olaraq araşdıraq:

1) Funksiya nöqtədə müəyyən edilməmişdir, ona görə də dərhal deyə bilərik ki, onun üzərində davamlı deyil.

2) Bunun üçün fasiləsizliyin xarakterini təyin edək, birtərəfli limitləri hesablayırıq;

Birtərəfli limitlər sonlu və fərqlidir, yəni funksiya nöqtədə sıçrayışla 1-ci növ fasiləsizliyə məruz qalır. Bir daha qeyd edək ki, limitləri taparkən, kəsilmə nöqtəsində funksiyanın müəyyən edilib-edilməməsinin əhəmiyyəti yoxdur.

İndi yalnız rəsmləri qaralamadan köçürmək (sanki tədqiqatın köməyi ilə hazırlanmışdır ;-)) və tapşırığı yerinə yetirməkdir:

Cavab verin: funksiya sıçrayışla birinci növ fasiləsizliyə məruz qaldığı nöqtə istisna olmaqla, bütün say xəttində davamlıdır.

Bəzən onlar fasiləsiz atlamanın əlavə göstəricisini tələb edirlər. Sadəcə hesablanır - sağ limitdən sol həddi çıxarmaq lazımdır: , yəni fasilə nöqtəsində funksiyamız 2 vahid aşağı sıçradı (mənfi işarənin bizə dediyi kimi).

Misal 3

Funksiyanı araşdırın davamlılıq üçün. Funksiya kəsiklərinin xarakterini, əgər varsa, müəyyən edin. Rəsm çəkin.

Bu, özünüz həll edə biləcəyiniz bir nümunə, dərsin sonunda nümunə həlldir.

Funksiya üç hissədən ibarət olduqda tapşırığın ən populyar və geniş yayılmış versiyasına keçək:

Misal 4

Funksiyanı fasiləsizliyə görə yoxlayın və funksiyanın qrafikini çəkin .

Həll: aydındır ki, funksiyanın hər üç hissəsi müvafiq intervallarda davamlıdır, ona görə də parçalar arasında yalnız iki “qovşaq” nöqtəsini yoxlamaq qalır. Əvvəlcə bir qaralama çəkək, məqalənin birinci hissəsində tikinti texnikasını kifayət qədər ətraflı şərh etdim; Yeganə odur ki, tək nöqtələrimizi diqqətlə izləməliyik: bərabərsizlik səbəbindən qiymət düz xəttə (yaşıl nöqtə), bərabərsizlik səbəbindən isə dəyər parabolaya (qırmızı nöqtə) aiddir:


Yaxşı, prinsipcə, hər şey aydındır =) Qərarın rəsmiləşdirilməsi qalır. İki "birləşmə" nöqtəsinin hər biri üçün biz standart olaraq 3 davamlılıq şərtini yoxlayırıq:

mən) Davamlılıq üçün nöqtəni araşdırırıq

1)

Birtərəfli limitlər sonlu və fərqlidir, yəni funksiya nöqtədə sıçrayışla 1-ci növ fasiləsizliyə məruz qalır.

Kesiklik sıçrayışını sağ və sol sərhədlər arasındakı fərq kimi hesablayaq:
, yəni qrafik bir vahid yuxarı qalxdı.

II) Davamlılıq üçün nöqtəni araşdırırıq

1) – funksiya verilmiş nöqtədə müəyyən edilir.

2) Birtərəfli məhdudiyyətləri tapın:

– birtərəfli limitlər sonlu və bərabərdir, yəni ümumi hədd var.

3) – bir nöqtədə funksiyanın həddi bu funksiyanın verilmiş nöqtədəki qiymətinə bərabərdir.

Son mərhələdə rəsmini son versiyaya köçürürük, bundan sonra son akkordu qoyuruq:

Cavab verin: funksiya sıçrayışla birinci növ fasiləsizliyə məruz qaldığı nöqtə istisna olmaqla, bütün say xəttində davamlıdır.

Misal 5

Funksiyanı fasiləsizliyə görə yoxlayın və onun qrafikini qurun .

Bu, özünüz həll etməyiniz üçün bir nümunədir, qısa həll və dərsin sonunda tapşırığın təxmini nümunəsi.

Sizdə belə bir təəssürat yarana bilər ki, bir nöqtədə funksiya davamlı olmalıdır, digərində isə fasilə olmalıdır. Praktikada bu həmişə belə olmur. Qalan nümunələri laqeyd etməməyə çalışın - bir neçə maraqlı və vacib xüsusiyyət olacaq:

Misal 6

Funksiya verilmişdir . Nöqtələrdə davamlılıq funksiyasını araşdırın. Qrafik qurun.

Həll: və yenidən dərhal qaralama üzərində rəsm icra edin:

Bu qrafikin özəlliyi ondan ibarətdir ki, hissə-hissə funksiyası absis oxunun tənliyi ilə verilir. Bu sahə burada çəkilib yaşıl, və notebookda adətən sadə qələmlə qalın hərflərlə vurğulanır. Və əlbəttə ki, qoçlarımızı unutma: dəyər tangens budağa (qırmızı nöqtə) aiddir və dəyər düz xəttə aiddir.

Rəsmdən hər şey aydındır - funksiya bütün nömrə xətti boyunca davamlıdır, yalnız 3-4 oxşar nümunədən sonra tam avtomatlaşdırmaya gətirilən həlli rəsmiləşdirmək qalır:

mən) Davamlılıq üçün nöqtəni araşdırırıq

1) – funksiya verilmiş nöqtədə müəyyən edilir.

2) Birtərəfli limitləri hesablayaq:

, yəni ümumi limit var.

İstənilən halda, sizə cüzi bir faktı xatırlatmağa icazə verin: sabitin həddi sabitin özünə bərabərdir. Bu halda, sıfırın həddi sıfırın özünə bərabərdir (sol əlli həddi).

3) – bir nöqtədə funksiyanın həddi bu funksiyanın verilmiş nöqtədəki qiymətinə bərabərdir.

Beləliklə, bir nöqtədə funksiyanın davamlılığının təyini ilə bir nöqtədə fasiləsizdir.

II) Davamlılıq üçün nöqtəni araşdırırıq

1) – funksiya verilmiş nöqtədə müəyyən edilir.

2) Birtərəfli məhdudiyyətləri tapın:

Və burada - birinin həddi vahidin özünə bərabərdir.

- Ümumi məhdudiyyət var.

3) – bir nöqtədə funksiyanın həddi bu funksiyanın verilmiş nöqtədəki qiymətinə bərabərdir.

Beləliklə, bir nöqtədə funksiyanın davamlılığının təyini ilə bir nöqtədə fasiləsizdir.

Həmişə olduğu kimi, araşdırmadan sonra rəsmimizi son versiyaya köçürürük.

Cavab verin: funksiya nöqtələrdə davamlıdır.

Nəzərə alın ki, bir şərtlə ki, bizdən davamlılıq üçün bütün funksiyanın öyrənilməsi ilə bağlı heç nə tələb olunmayıb və formalaşdırmaq üçün yaxşı riyazi forma hesab olunur. dəqiq və aydın verilən sualın cavabı. Yeri gəlmişkən, əgər şərt sizdən qrafik qurmağı tələb etmirsə, deməli sizdə var hər haqqı onu qurmayın (baxmayaraq ki, müəllim sizi sonradan bunu etməyə məcbur edə bilər).

Bunu özünüz həll etmək üçün kiçik bir riyazi "dil bükmə":

Misal 7

Funksiya verilmişdir . Nöqtələrdə davamlılıq funksiyasını araşdırın. Əgər varsa, kəsilmə nöqtələrini təsnif edin. Rəsmi icra edin.

Bütün "sözləri" düzgün "tələffüz etməyə" çalışın =) Və qrafiki daha dəqiq çəkin, dəqiqlik, hər yerdə artıq olmaz;-)

Yadınızdadırsa, mən rəsmləri dərhal qaralama şəklində tamamlamağı tövsiyə etdim, lakin vaxtaşırı qrafikin nəyə bənzədiyini dərhal anlaya bilməyəcəyiniz nümunələrə rast gəlirsiniz. Buna görə də, bəzi hallarda, əvvəlcə birtərəfli hədləri tapmaq və yalnız bundan sonra, tədqiqata əsaslanaraq, budaqları təsvir etmək sərfəlidir. Son iki nümunədə bəzi birtərəfli limitlərin hesablanması texnikasını da öyrənəcəyik:

Misal 8

Funksiyanı fasiləsizliyə görə yoxlayın və onun sxematik qrafikini qurun.

Həll: pis nöqtələr göz qabağındadır: (göstəricinin məxrəcini sıfıra endirir) və (bütün kəsrin məxrəcini sıfıra endirir). Bu funksiyanın qrafikinin necə göründüyü aydın deyil, yəni əvvəlcə bəzi araşdırmalar aparmaq daha yaxşıdır.