Jak řešit soustavy lineárních rovnic Gaussovou metodou. Opačná metoda Gaussovy metody

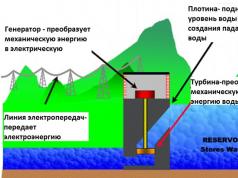
Zde můžete systém zdarma vyřešit lineární rovnice Gaussova metoda online velké velikosti v komplexních číslech s velmi podrobným řešením. Naše kalkulačka dokáže online řešit běžné určité i neurčité soustavy lineárních rovnic pomocí Gaussovy metody, která má nekonečný počet řešení. V tomto případě v odpovědi dostanete závislost některých proměnných přes jiné, volné. Konzistenci systému rovnic můžete také zkontrolovat online pomocí Gaussova řešení.

2 Velikost matice: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 93 343 31 4 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 89 75 88 83 77 78 75 8 80 78 79 80 80 90 91 92 93 94 95 96 97 98 20 100 X 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 3 53 3 3 4 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 84 83 81 81 91 92 93 94 95 96 97 98 99 100 101

O metodě

Při řešení soustavy lineárních rovnic online metoda Gauss jsou provedeny následující kroky.

1. Píšeme rozšířenou matici.
2. Ve skutečnosti je řešení rozděleno na kroky vpřed a vzad Gaussovy metody. Přímým přístupem Gaussovy metody je redukce matice na stupňovitou formu. Opakem Gaussovy metody je redukce matice na speciální stupňovitou formu. V praxi je ale pohodlnější okamžitě vynulovat to, co se nachází nad i pod dotyčným prvkem. Naše kalkulačka používá přesně tento přístup.
3. Je důležité si uvědomit, že při řešení pomocí Gaussovy metody je přítomnost alespoň jednoho nulového řádku v matici s NE nulou pravá strana(sloupec volných členů) označuje nekompatibilitu systému. Řešení lineární systém v tomto případě neexistuje.

Chcete-li co nejlépe pochopit, jak Gaussův algoritmus funguje online, zadejte libovolný příklad, vyberte „velmi podrobné řešení“ a prohlédněte si jeho řešení online.

Gaussova metoda, nazývaná také metoda sekvenční eliminace neznámé je následující. Pomocí elementárních transformací je soustava lineárních rovnic uvedena do takové podoby, že její matice koeficientů se ukáže jako lichoběžníkový (stejný jako trojúhelníkový nebo stupňovitý) nebo blízko lichoběžníkovému (přímý tah Gaussovy metody, dále - jednoduše přímý tah). Příklad takového systému a jeho řešení je na obrázku výše.

V takovém systému poslední rovnice obsahuje pouze jednu proměnnou a její hodnotu lze jednoznačně zjistit. Hodnota této proměnné se pak dosadí do předchozí rovnice ( inverzní ke Gaussově metodě , pak jen obráceně), ze které je nalezena předchozí proměnná a tak dále.

V lichoběžníkovém (trojúhelníkovém) systému, jak vidíme, třetí rovnice již neobsahuje proměnné y A X a druhá rovnice je proměnná X .

Poté, co matice systému nabyla lichoběžníkového tvaru, již není těžké porozumět problematice kompatibility systému, určit počet řešení a najít řešení samotná.

Výhody metody:

1. při řešení soustav lineárních rovnic s více než třemi rovnicemi a neznámými není Gaussova metoda tak těžkopádná jako Cramerova metoda, protože řešení Gaussovou metodou vyžaduje méně výpočtů;
2. Pomocí Gaussovy metody lze řešit neurčité soustavy lineárních rovnic, tedy mít společné rozhodnutí(a podíváme se na ně v této lekci), ale pomocí Cramerovy metody můžeme pouze konstatovat, že systém je nejistý;
3. můžete řešit soustavy lineárních rovnic, ve kterých počet neznámých není roven počtu rovnic (v této lekci je také rozebereme);
4. Metoda je založena na elementárních (školních) metodách - metodě dosazování neznámých a metodě sčítání rovnic, kterých jsme se dotkli v odpovídajícím článku.

Aby každý pochopil jednoduchost, s jakou se řeší lichoběžníkové (trojúhelníkové, stupňovité) soustavy lineárních rovnic, uvádíme řešení takové soustavy pomocí zpětného pohybu. Rychlé rozhodnutí Tento systém byl znázorněn na obrázku na začátku lekce.

Příklad 1 Vyřešte soustavu lineárních rovnic pomocí inverze:

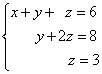
Řešení. V tomto lichoběžníkovém systému proměnná z lze jednoznačně nalézt ze třetí rovnice. Její hodnotu dosadíme do druhé rovnice a získáme hodnotu proměnné y:

Nyní známe hodnoty dvou proměnných - z A y. Dosadíme je do první rovnice a získáme hodnotu proměnné X:

Z předchozích kroků vypíšeme řešení soustavy rovnic:

Pro získání takovéto lichoběžníkové soustavy lineárních rovnic, kterou jsme řešili velmi jednoduše, je nutné použít dopředný zdvih spojený s elementárními transformacemi soustavy lineárních rovnic. Taky to není moc těžké.

Elementární transformace soustavy lineárních rovnic

Opakováním školní metody algebraického sčítání rovnic soustavy jsme zjistili, že k jedné z rovnic soustavy můžeme přidat další rovnici soustavy a každou z rovnic lze vynásobit nějakými čísly. Výsledkem je soustava lineárních rovnic ekvivalentní této soustavě. V něm již jedna rovnice obsahovala pouze jednu proměnnou, jejíž dosazením hodnoty do jiných rovnic dojdeme k řešení. Takové přidání je jedním z typů elementární transformace systému. Při použití Gaussovy metody můžeme použít několik typů transformací.

Animace výše ukazuje, jak se soustava rovnic postupně mění v lichoběžníkovou. Tedy ten, který jste viděli v úplně první animaci a přesvědčili se, že je snadné v něm najít hodnoty všech neznámých. Jak takovou transformaci provést a samozřejmě příklady budou diskutovány dále.

Při řešení soustav lineárních rovnic s libovolným počtem rovnic a neznámých v soustavě rovnic a v rozšířené matici soustavy Umět:

1. přeuspořádat řádky (to bylo zmíněno na samém začátku tohoto článku);
2. pokud jiné transformace vedou ke stejným nebo proporcionálním řádkům, lze je smazat, s výjimkou jednoho;
3. odstranit „nulové“ řádky, kde jsou všechny koeficienty rovny nule;
4. vynásobte nebo vydělte libovolný řetězec určitým číslem;
5. k libovolnému řádku přidejte další řádek, vynásobený určitým číslem.

Výsledkem transformací je soustava lineárních rovnic ekvivalentní této soustavě.

Algoritmus a příklady řešení soustavy lineárních rovnic se čtvercovou maticí soustavy pomocí Gaussovy metody

Uvažujme nejprve řešení soustav lineárních rovnic, ve kterých je počet neznámých roven počtu rovnic. Matice takového systému je čtvercová, to znamená, že počet řádků v ní se rovná počtu sloupců.

Příklad 2Řešte soustavu lineárních rovnic pomocí Gaussovy metody

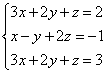
Při řešení soustav lineárních rovnic školními metodami jsme jednu z rovnic člen po členu násobili určitým číslem, takže koeficienty první proměnné v obou rovnicích byla opačná čísla. Při sčítání rovnic tato proměnná odpadá. Podobně funguje Gaussova metoda.

Pro zjednodušení vzhledřešení pojďme vytvořit rozšířenou matici systému:

V této matici jsou koeficienty neznámých umístěny vlevo před svislou čarou a volné členy jsou umístěny vpravo za svislou čarou.

Pro usnadnění dělení koeficientů pro proměnné (pro získání dělení jednotkou) Prohodíme první a druhý řádek systémové matice. Získáme systém ekvivalentní tomuto, protože v systému lineárních rovnic lze rovnice zaměňovat:

Pomocí nové první rovnice odstranit proměnnou X z druhé a všech následujících rovnic. K tomu přidáme do druhého řádku matice první řádek vynásobený (v našem případě ), do třetího řádku - první řádek vynásobený (v našem případě ).

To je možné, protože

Kdyby naše soustava rovnic měla více než tři, pak by bylo nutné do všech následujících rovnic přidat první řádek, vynásobený poměrem odpovídajících koeficientů, braný se znaménkem mínus.

V důsledku toho získáme matici ekvivalentní tomuto systému nového systému rovnic, ve kterém všechny rovnice počínaje druhým neobsahují proměnnou X :

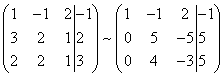
Pro zjednodušení druhého řádku výsledného systému jej vynásobte a znovu získáte matici soustavy rovnic ekvivalentní této soustavě:

Nyní ponecháme první rovnici výsledného systému nezměněnou, pomocí druhé rovnice eliminujeme proměnnou y ze všech následujících rovnic. K tomu přidáme ke třetímu řádku systémové matice druhý řádek, vynásobený (v našem případě ).

Pokud by v našem systému bylo více než tři rovnice, pak bychom ke všem následujícím rovnicím museli přidat druhý řádek, vynásobený poměrem odpovídajících koeficientů braných se znaménkem mínus.

Výsledkem je, že opět získáme matici systému ekvivalentního tomuto systému lineárních rovnic:

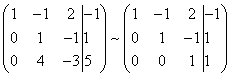
Získali jsme ekvivalentní lichoběžníkový systém lineárních rovnic:

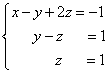
Pokud je počet rovnic a proměnných větší než v našem příkladu, pak proces postupného odstraňování proměnných pokračuje, dokud se matice systému nestane lichoběžníkovým, jako v našem ukázkovém příkladu.

Najdeme řešení „od konce“ - zpětný pohyb. Pro tohle z poslední rovnice určíme z:
.
Dosazením této hodnoty do předchozí rovnice najdeme y:

Z první rovnice najdeme X:

Odpověď: řešení této soustavy rovnic je .

: v tomto případě bude dána stejná odpověď, pokud má systém jedinečné řešení. Pokud má systém nekonečný počet řešení, pak toto bude odpověď a to je předmětem páté části této lekce.

Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody sami a pak se podívejte na řešení

Opět zde máme příklad konzistentního a určitého systému lineárních rovnic, ve kterém je počet rovnic roven počtu neznámých. Rozdíl oproti našemu ukázkovému příkladu z algoritmu je ten, že již existují čtyři rovnice a čtyři neznámé.

Příklad 4. Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody:

Nyní musíte použít druhou rovnici k odstranění proměnné z následujících rovnic. Pojďme provést přípravné práce. Aby to bylo s poměrem koeficientů pohodlnější, musíte jeden dostat do druhého sloupce druhého řádku. Chcete-li to provést, odečtěte třetí od druhého řádku a výsledný druhý řádek vynásobte -1.

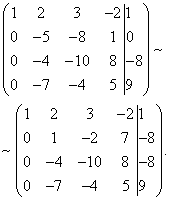
Proveďme nyní vlastní eliminaci proměnné ze třetí a čtvrté rovnice. Chcete-li to provést, přidejte druhý řádek, vynásobený , ke třetímu řádku a druhý, násobený , ke čtvrtému řádku.

Nyní pomocí třetí rovnice odstraníme proměnnou ze čtvrté rovnice. Chcete-li to provést, přidejte třetí řádek ke čtvrtému řádku, vynásobený . Získáme rozšířenou lichoběžníkovou matrici.

Získali jsme soustavu rovnic, která je ekvivalentní tento systém:

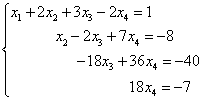
Výsledné a dané systémy jsou tedy kompatibilní a jednoznačné. Konečné rozhodnutí najdeme „od konce“. Ze čtvrté rovnice můžeme přímo vyjádřit hodnotu proměnné „x-čtyři“:

Tuto hodnotu dosadíme do třetí rovnice soustavy a dostaneme

,

,

Nakonec substituce hodnot

První rovnice dává

,

kde najdeme „x první“:

Odpověď: tato soustava rovnic má jedinečné řešení .

Řešení systému můžete také zkontrolovat na kalkulačce Cramerovou metodou: v tomto případě bude stejná odpověď poskytnuta, pokud má systém jedinečné řešení.

Řešení aplikovaných úloh pomocí Gaussovy metody na příkladu úlohy na slitinách

Systémy lineárních rovnic se používají k modelování reálných objektů ve fyzickém světě. Pojďme vyřešit jeden z těchto problémů - slitiny. Podobné problémy - problémy na směsích, náklady popř specifická gravitace jednotlivé zboží ve skupině produktů a podobně.

Příklad 5. Tři kusy slitiny mají celkovou hmotnost 150 kg. První slitina obsahuje 60% mědi, druhá - 30%, třetí - 10%. Navíc ve druhé a třetí slitině dohromady je o 28,4 kg mědi méně než v první slitině a ve třetí slitině je o 6,2 kg méně mědi než ve druhé. Najděte hmotnost každého kusu slitiny.

Řešení. Sestavíme soustavu lineárních rovnic:

Vynásobíme druhou a třetí rovnici 10, získáme ekvivalentní systém lineárních rovnic:

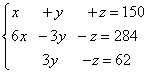
Vytvoříme rozšířenou matici systému:

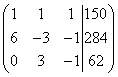
Pozor, přímo vpřed. Přičtením (v našem případě odečtením) jednoho řádku vynásobeného číslem (aplikujeme dvakrát) dochází s rozšířenou maticí systému k následujícím transformacím:

Přímý tah je u konce. Získali jsme expandovanou lichoběžníkovou matrici.

Aplikujeme zpětný pohyb. Najdeme řešení od konce. To vidíme.

Z druhé rovnice zjistíme

Ze třetí rovnice -

Řešení systému můžete také zkontrolovat na kalkulačce Cramerovou metodou: v tomto případě bude stejná odpověď poskytnuta, pokud má systém jedinečné řešení.

O jednoduchosti Gaussovy metody svědčí i to, že německému matematikovi Carlu Friedrichu Gaussovi trvalo její vynalezení pouhých 15 minut. Kromě po něm pojmenované metody je z Gaussových děl známé rčení „Neměli bychom zaměňovat to, co se nám zdá neuvěřitelné a nepřirozené, s naprosto nemožným“ – jakýsi druh stručné pokyny dělat objevy.

V mnoha aplikovaných úlohách nemusí existovat třetí omezení, tedy třetí rovnice, pak musíte řešit soustavu dvou rovnic o třech neznámých pomocí Gaussovy metody, nebo naopak neznámých je méně než rovnic. Nyní začneme takové soustavy rovnic řešit.

Pomocí Gaussovy metody můžete určit, zda je některý systém kompatibilní nebo nekompatibilní n lineární rovnice s n proměnné.

Gaussova metoda a soustavy lineárních rovnic s nekonečným počtem řešení

Dalším příkladem je konzistentní, ale neurčitý systém lineárních rovnic, to znamená, že má nekonečný počet řešení.

Po provedení transformací v rozšířené matici systému (přeuspořádání řádků, násobení a dělení řádků určitým číslem, přidání dalšího k jednomu řádku) se mohly objevit řádky formuláře

Pokud ve všech rovnicích majících tvar

Volné členy se rovnají nule, to znamená, že systém je neurčitý, to znamená, že má nekonečně mnoho řešení a rovnice tohoto typu jsou „nadbytečné“ a ze systému je vyřazujeme.

Příklad 6.

Řešení. Vytvořme rozšířenou matici systému. Potom pomocí první rovnice odstraníme proměnnou z následujících rovnic. Chcete-li to provést, přidejte do druhého, třetího a čtvrtého řádku první, vynásobený:

Nyní přidáme druhý řádek ke třetímu a čtvrtému.

V důsledku toho se dostáváme k systému

Poslední dvě rovnice se změnily na rovnice tvaru. Tyto rovnice jsou splněny pro jakoukoli hodnotu neznámých a lze je vyřadit.

Abychom splnili druhou rovnici, můžeme zvolit libovolné hodnoty pro a , pak bude hodnota pro určena jednoznačně: . Z první rovnice je hodnota pro také nalezena jednoznačně: .

Daný i poslední systém jsou konzistentní, ale nejisté, a vzorce

pro libovolné a dejte nám všechna řešení daného systému.

Gaussova metoda a soustavy lineárních rovnic bez řešení

Dalším příkladem je nekonzistentní systém lineárních rovnic, tedy takový, který nemá řešení. Odpověď na takové problémy je formulována takto: systém nemá řešení.

Jak již bylo zmíněno v souvislosti s prvním příkladem, po provedení transformací se v rozšířené matici systému mohly objevit řádky formuláře

odpovídající rovnici tvaru

Pokud mezi nimi existuje alespoň jedna rovnice s nenulovým volným členem (tj. ), pak je tato soustava rovnic nekonzistentní, to znamená, že nemá řešení a její řešení je úplné.

Příklad 7. Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody:

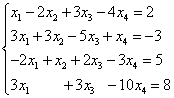
Řešení. Skládáme rozšířenou matici systému. Pomocí první rovnice vyloučíme proměnnou z následujících rovnic. Chcete-li to provést, přidejte první řádek vynásobený druhým řádkem, první řádek vynásobený třetím řádkem a první řádek vynásobený čtvrtým řádkem.

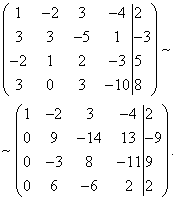
Nyní musíte použít druhou rovnici k odstranění proměnné z následujících rovnic. Abychom získali celočíselné poměry koeficientů, prohodíme druhý a třetí řádek rozšířené matice systému.

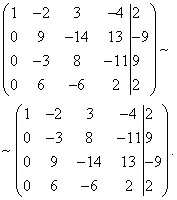
Chcete-li vyloučit třetí a čtvrtou rovnici, přidejte druhou vynásobenou , na třetí řádek a druhou násobenou , do čtvrtého řádku.

Nyní pomocí třetí rovnice odstraníme proměnnou ze čtvrté rovnice. Chcete-li to provést, přidejte třetí řádek ke čtvrtému řádku, vynásobený .

Daný systém je tedy ekvivalentní následujícímu:

Výsledný systém je nekonzistentní, protože jeho poslední rovnice nemůže být splněna žádnými hodnotami neznámých. Proto tento systém nemá řešení.

Gaussova metoda ideální pro řešení soustav lineárních algebraických rovnic (SLAE). Ve srovnání s jinými metodami má řadu výhod:

• za prvé, není třeba nejprve zkoumat konzistenci soustavy rovnic;
• za druhé, Gaussova metoda dokáže řešit nejen SLAE, ve kterých se počet rovnic shoduje s počtem neznámých proměnných a hlavní matice systému je nesingulární, ale také soustavy rovnic, ve kterých se počet rovnic neshoduje s počet neznámých proměnných nebo determinant hlavní matice je roven nule;
• za třetí, Gaussova metoda vede k výsledkům s relativně malým počtem výpočetních operací.

Stručný přehled článku.

Nejprve uvedeme potřebné definice a zavedeme notaci.

Dále popíšeme algoritmus Gaussovy metody pro nejjednodušší případ, tedy pro soustavy lineárních algebraických rovnic, počet rovnic, ve kterých se shoduje s počtem neznámých proměnných a determinantem hlavní matice soustavy je nerovná se nule. Při řešení takových soustav rovnic je nejzřetelněji patrná podstata Gaussovy metody, kterou je sekvenční eliminace neznámých proměnných. Proto se Gaussově metodě říká také metoda sekvenční eliminace neznámých. Ukážeme si detailní řešení několika příkladů.

Na závěr budeme uvažovat o řešení Gaussovou metodou systémů lineárních algebraických rovnic, jejichž hlavní matice je buď pravoúhlá nebo singulární. Řešení takových systémů má některé vlastnosti, které si podrobně prověříme na příkladech.

Navigace na stránce.

Základní definice a zápisy.

Uvažujme soustavu p lineárních rovnic s n neznámými (p se může rovnat n):

Kde jsou neznámé proměnné, jsou čísla (reálná nebo komplexní) a jsou volné členy.

Li , pak se nazývá soustava lineárních algebraických rovnic homogenní, v opačném případě - heterogenní.

Nazývá se množina hodnot neznámých proměnných, pro které se všechny rovnice systému stávají identitami rozhodnutí SLAU.

Pokud existuje alespoň jedno řešení soustavy lineárních algebraických rovnic, pak se nazývá kloub, v opačném případě - nespojující.

Pokud má SLAE jedinečné řešení, pak se nazývá určitý. Pokud existuje více než jedno řešení, zavolá se systém nejistý.

Říkají, že systém je napsaný souřadnicový tvar, pokud má formu
.

Tento systém v matricový formulář záznamů má tvar , kde - hlavní matice SLAE, - matice sloupce neznámých proměnných, - matice volných členů.

Přidáme-li k matici A jako (n+1)-tý sloupec matici-sloupec volných členů, dostaneme tzv. rozšířená matice soustav lineárních rovnic. Rozšířená matice je obvykle označena písmenem T a sloupec volných výrazů je oddělen svislou čarou od zbývajících sloupců, tj.

Čtvercová matice A se nazývá degenerovat, je-li jeho determinant nulový. Jestliže , pak se volá matice A nedegenerované.

Je třeba poznamenat následující bod.

Provedeme-li se soustavou lineárních algebraických rovnic následující akce

• prohodit dvě rovnice,
• vynásobte obě strany libovolné rovnice libovolným a nenulovým reálným (nebo komplexním) číslem k,
• k oběma stranám libovolné rovnice přidejte odpovídající části jiné rovnice, vynásobené libovolným číslem k,

pak dostanete ekvivalentní systém, který má stejná řešení (nebo stejně jako ten původní nemá žádná řešení).

Pro rozšířenou matici systému lineárních algebraických rovnic budou tyto akce znamenat provedení elementárních transformací s řádky:

• prohození dvou řádků,
• vynásobením všech prvků libovolné řady matice T nenulovým číslem k,
• přičtení k prvkům libovolného řádku matice odpovídající prvky jiného řádku, vynásobené libovolným číslem k.

Nyní můžeme přistoupit k popisu Gaussovy metody.

Řešení soustav lineárních algebraických rovnic, ve kterých je počet rovnic roven počtu neznámých a hlavní matice soustavy je nesingulární, pomocí Gaussovy metody.

Co bychom dělali ve škole, kdybychom dostali za úkol najít řešení soustavy rovnic? .

Někteří by to udělali.

Všimněte si, že přidávání na levou stranu druhé rovnice levá strana nejprve a na pravé straně - na pravé straně se můžete zbavit neznámých proměnných x 2 a x 3 a okamžitě najít x 1:

Nalezenou hodnotu x 1 =1 dosadíme do první a třetí rovnice soustavy:

Pokud obě strany třetí rovnice soustavy vynásobíme -1 a přičteme je k odpovídajícím částem první rovnice, zbavíme se neznámé proměnné x 3 a můžeme najít x 2:

Výslednou hodnotu x 2 = 2 dosadíme do třetí rovnice a najdeme zbývající neznámou proměnnou x 3:

Jiní by to udělali jinak.

Vyřešme první rovnici soustavy vzhledem k neznámé proměnné x 1 a výsledný výraz dosadíme do druhé a třetí rovnice soustavy, abychom z nich tuto proměnnou vyloučili:

Nyní vyřešme druhou rovnici systému pro x 2 a výsledný výsledek dosadíme do třetí rovnice, abychom z ní odstranili neznámou proměnnou x 2:

Ze třetí rovnice soustavy je zřejmé, že x 3 =3. Z druhé rovnice zjistíme a z první rovnice dostaneme .

Známá řešení, že?

Nejzajímavější na tom je, že druhá metoda řešení je v podstatě metoda sekvenční eliminace neznámých, tedy Gaussova metoda. Když jsme vyjádřili neznámé proměnné (nejprve x 1, v další fázi x 2) a dosadili je do zbývajících rovnic systému, tím jsme je vyloučili. Prováděli jsme eliminaci, dokud v poslední rovnici nezůstala pouze jedna neznámá proměnná. Proces postupného odstraňování neznámých se nazývá přímou Gaussovou metodou. Po dokončení tah vpřed nyní máme možnost vypočítat neznámou proměnnou v poslední rovnici. S jeho pomocí najdeme další neznámou proměnnou z předposlední rovnice a tak dále. Proces postupného hledání neznámých proměnných při přechodu od poslední rovnice k první se nazývá inverzní ke Gaussově metodě.

Je třeba poznamenat, že když vyjádříme x 1 pomocí x 2 a x 3 v první rovnici a poté dosadíme výsledný výraz do druhé a třetí rovnice, vedou následující akce ke stejnému výsledku:

Takový postup skutečně také umožňuje eliminovat neznámou proměnnou x 1 z druhé a třetí rovnice systému:

Nuance s eliminací neznámých proměnných pomocí Gaussovy metody vznikají tehdy, když rovnice systému neobsahují nějaké proměnné.

Například v SLAU v první rovnici není žádná neznámá proměnná x 1 (jinými slovy koeficient před ní je nula). Nemůžeme tedy vyřešit první rovnici soustavy pro x 1, abychom tuto neznámou proměnnou odstranili ze zbývajících rovnic. Cesta z této situace je prohození rovnic systému. Protože uvažujeme soustavy lineárních rovnic, jejichž determinanty hlavních matic jsou odlišné od nuly, vždy existuje rovnice, ve které je proměnná, kterou potřebujeme, přítomna, a tuto rovnici můžeme přeskupit do požadované polohy. Pro náš příklad stačí prohodit první a druhou rovnici soustavy , pak můžete vyřešit první rovnici pro x 1 a vyloučit ji ze zbývajících rovnic systému (ačkoli x 1 již ve druhé rovnici není).

Doufáme, že pochopíte podstatu.

Pojďme si popsat Algoritmus Gaussovy metody.

Předpokládejme, že potřebujeme vyřešit systém n lineárních algebraických rovnic s n neznámými proměnné formuláře , a nechť je determinant jeho hlavní matice odlišný od nuly.

Budeme předpokládat, že , protože toho můžeme vždy dosáhnout přeskupením rovnic soustavy. Vynechme neznámou proměnnou x 1 ze všech rovnic soustavy, počínaje druhou. Abychom to udělali, ke druhé rovnici soustavy přidáme první, vynásobenou , ke třetí rovnici přidáme první, vynásobenou a tak dále, k n-té rovnici přidáme první, vynásobenou . Systém rovnic po takových transformacích nabude tvaru

kde a .

Ke stejnému výsledku bychom dospěli, kdybychom x 1 vyjádřili pomocí jiných neznámých proměnných v první rovnici soustavy a výsledný výraz dosadili do všech ostatních rovnic. Proměnná x 1 je tedy vyloučena ze všech rovnic, počínaje druhou.

Dále postupujeme obdobně, ale pouze s částí výsledné soustavy, která je vyznačena na obrázku

Abychom to udělali, ke třetí rovnici soustavy přidáme druhou, vynásobenou , ke čtvrté rovnici přidáme druhou, vynásobenou , atd., k n-té rovnici přidáme druhou, vynásobenou . Systém rovnic po takových transformacích nabude tvaru

kde a . Proměnná x 2 je tedy vyloučena ze všech rovnic, počínaje třetí.

Dále přistoupíme k eliminaci neznámého x 3, přičemž obdobně postupujeme s částí systému vyznačenou na obrázku

Pokračujeme tedy v přímém postupu Gaussovy metody, dokud systém nezíská formu

Od tohoto okamžiku začínáme obráceně Gaussovy metody: x n vypočítáme z poslední rovnice jako , pomocí získané hodnoty x n zjistíme x n-1 z předposlední rovnice atd., zjistíme x 1 z první rovnice .

Podívejme se na algoritmus na příkladu.

Příklad.

Gaussova metoda.

Řešení.

Koeficient a 11 je nenulový, přistoupíme tedy k přímé progresi Gaussovy metody, tedy k vyloučení neznámé proměnné x 1 ze všech rovnic soustavy kromě první. Chcete-li to provést, přidejte k levé a pravé straně druhé, třetí a čtvrté rovnice levou a pravou stranu první rovnice vynásobené , resp. A :

Neznámá proměnná x 1 byla eliminována, přejděme k eliminaci x 2 . K levé a pravé straně třetí a čtvrté rovnice soustavy přidáme levou a pravou stranu druhé rovnice, vynásobené příslušně A :

Abychom dokončili dopřednou progresi Gaussovy metody, musíme z poslední rovnice systému odstranit neznámou proměnnou x 3. Přidejme k levé a pravé straně čtvrté rovnice, respektive k levé a pravé straně třetí rovnice, vynásobené :

Můžete začít obráceně Gaussovy metody.

Z poslední rovnice, kterou máme ,
ze třetí rovnice dostaneme,
od druhého,
z toho prvního.

Pro kontrolu můžete získané hodnoty neznámých proměnných dosadit do původní soustavy rovnic. Všechny rovnice se změní na identity, což naznačuje, že řešení pomocí Gaussovy metody bylo nalezeno správně.

Odpovědět:

Nyní uveďme řešení stejného příkladu pomocí Gaussovy metody v maticovém zápisu.

Příklad.

Najděte řešení soustavy rovnic Gaussova metoda.

Řešení.

Rozšířená matice systému má tvar . V horní části každého sloupce jsou neznámé proměnné, které odpovídají prvkům matice.

Přímý přístup Gaussovy metody zde zahrnuje redukci rozšířené matice systému do lichoběžníkového tvaru pomocí elementárních transformací. Tento proces je podobný eliminaci neznámých proměnných, kterou jsme provedli se systémem v souřadnicové formě. Nyní uvidíte toto.

Transformujme matici tak, aby všechny prvky v prvním sloupci, počínaje druhým, byly nulové. Za tímto účelem k prvkům druhého, třetího a čtvrtého řádku přidáme odpovídající prvky prvního řádku vynásobené , a podle toho:

Dále transformujeme výslednou matici tak, aby ve druhém sloupci všechny prvky, počínaje třetím, byly nulové. To by odpovídalo eliminaci neznámé proměnné x 2 . Za tímto účelem k prvkům třetího a čtvrtého řádku přidáme odpovídající prvky prvního řádku matice, vynásobené resp. A :

Zbývá vyloučit neznámou proměnnou x 3 z poslední rovnice soustavy. Za tímto účelem k prvkům posledního řádku výsledné matice přidáme odpovídající prvky předposledního řádku, vynásobené :

Je třeba poznamenat, že tato matice odpovídá soustavě lineárních rovnic

který byl získán dříve po pohybu vpřed.

Je čas se vrátit. V maticovém zápisu inverze ke Gaussově metodě zahrnuje transformaci výsledné matice tak, aby matice označená na obrázku

se stal diagonálním, to znamená, že nabyl tvaru

kde jsou nějaká čísla.

Tyto transformace jsou podobné dopředným transformacím Gaussovy metody, ale neprovádějí se od prvního řádku k poslednímu, ale od posledního k prvnímu.

Přidejte k prvkům třetího, druhého a prvního řádku odpovídající prvky posledního řádku, vynásobené , dál a dál respektive:

Nyní přidejte k prvkům druhého a prvního řádku odpovídající prvky třetího řádku, vynásobené respektive:

V posledním kroku reverzní Gaussovy metody k prvkům prvního řádku přidáme odpovídající prvky druhého řádku, vynásobené:

Výsledná matice odpovídá soustavě rovnic , odkud najdeme neznámé proměnné.

Odpovědět:

POZNÁMKA.

Při použití Gaussovy metody k řešení soustav lineárních algebraických rovnic je třeba se vyhnout přibližným výpočtům, protože to může vést ke zcela nesprávným výsledkům. Doporučujeme nezaokrouhlovat desetinná místa. Lepší od desetinná místa jít do obyčejné zlomky.

Příklad.

Vyřešte soustavu tří rovnic pomocí Gaussovy metody .

Řešení.

Všimněte si, že v tomto příkladu mají neznámé proměnné jiné označení (ne x 1, x 2, x 3, ale x, y, z). Přejděme k obyčejným zlomkům:

Vynechme neznámou x z druhé a třetí rovnice soustavy:

Ve výsledném systému neznámá proměnná y chybí ve druhé rovnici, ale y je přítomna ve třetí rovnici, proto prohoďme druhou a třetí rovnici:

Tím je přímá progrese Gaussovy metody dokončena (není nutné vyloučit y ze třetí rovnice, protože tato neznámá proměnná již neexistuje).

Začněme opačným pohybem.

Z poslední rovnice najdeme ,
od předposledního


z první rovnice, kterou máme

Odpovědět:

X = 10, y = 5, z = -20.

Řešení soustav lineárních algebraických rovnic, ve kterých se počet rovnic neshoduje s počtem neznámých nebo je hlavní matice soustavy singulární, pomocí Gaussovy metody.

Soustavy rovnic, jejichž hlavní matice je pravoúhlá nebo čtvercová singulární, nemusí mít žádná řešení, mohou mít jediné řešení nebo mohou mít nekonečný počet řešení.

Nyní pochopíme, jak nám Gaussova metoda umožňuje stanovit kompatibilitu či nekonzistenci soustavy lineárních rovnic a v případě její kompatibility určit všechna řešení (nebo jediné řešení).

V zásadě zůstává proces eliminace neznámých proměnných v případě takových SLAE stejný. Nicméně stojí za to se podrobně zabývat některými situacemi, které mohou nastat.

Přejděme k nejdůležitější fázi.

Předpokládejme tedy, že systém lineárních algebraických rovnic po dokončení dopředné progrese Gaussovy metody získá tvar a ani jedna rovnice nebyla zredukována (v tomto případě bychom dospěli k závěru, že systém je nekompatibilní). Nabízí se logická otázka: „Co dělat dál“?

Zapišme si neznámé proměnné, které jsou na prvním místě ve všech rovnicích výsledného systému:

V našem příkladu to jsou x 1, x 4 a x 5. Na levých stranách rovnic soustavy ponecháme pouze ty členy, které obsahují zapsané neznámé proměnné x 1, x 4 a x 5, zbývající členy přeneseme na pravou stranu rovnic s opačným znaménkem:

Dejme neznámým proměnným, které jsou na pravé straně rovnic, libovolné hodnoty, kde - libovolná čísla:

Poté pravé strany všech rovnic našeho SLAE obsahují čísla a můžeme přistoupit k obrácení Gaussovy metody.

Z poslední rovnice soustavy, kterou máme, z předposlední rovnice najdeme, z první rovnice dostaneme

Řešením soustavy rovnic je množina hodnot neznámých proměnných

Dávání čísel různé hodnoty, získáme různá řešení soustavy rovnic. To znamená, že náš systém rovnic má nekonečně mnoho řešení.

Odpovědět:

Kde - libovolná čísla.

Pro konsolidaci materiálu podrobně rozebereme řešení několika dalších příkladů.

Příklad.

Rozhodni se homogenní systém lineární algebraické rovnice Gaussova metoda.

Řešení.

Vynechme neznámou proměnnou x z druhé a třetí rovnice soustavy. Za tímto účelem k levé a pravé straně druhé rovnice přidáme levou a pravou stranu první rovnice, vynásobené , a k levé a pravé straně třetí rovnice přidáme levou a pravou stranu první rovnice. pravé strany první rovnice, vynásobené:

Nyní vynechme y ze třetí rovnice výsledné soustavy rovnic:

Výsledný SLAE je ekvivalentní systému .

Na levé straně rovnic soustavy ponecháme pouze členy obsahující neznámé proměnné x a y a členy s neznámou proměnnou z přesuneme na pravou stranu:

Dvě soustavy lineárních rovnic se nazývají ekvivalentní, pokud se množina všech jejich řešení shoduje.

Elementární transformace soustavy rovnic jsou:

1. Vymazání triviálních rovnic ze systému, tzn. ty, u nichž jsou všechny koeficienty rovny nule;
2. Násobení libovolné rovnice číslem jiným než nula;
3. Přidání libovolné j-té rovnice vynásobené libovolným číslem k libovolné i-té rovnici.

Proměnná x i se nazývá volná, pokud tato proměnná není povolena, ale je povolen celý systém rovnic.

Teorém. Elementární transformace transformují soustavu rovnic na ekvivalentní.

Smyslem Gaussovy metody je transformovat původní systém rovnic a získat ekvivalentní vyřešený nebo ekvivalentní nekonzistentní systém.

Gaussova metoda se tedy skládá z následujících kroků:

1. Podívejme se na první rovnici. Zvolme první nenulový koeficient a vydělme jím celou rovnici. Získáme rovnici, do které vstupuje nějaká proměnná x i s koeficientem 1;
2. Odečteme tuto rovnici od všech ostatních a vynásobíme ji takovými čísly, aby koeficienty proměnné x i ve zbývajících rovnicích byly nulové. Získáme systém vyřešený vzhledem k proměnné x i a ekvivalentní původní;
3. Vzniknou-li triviální rovnice (zřídka, ale stává se to; např. 0 = 0), vyškrtneme je ze soustavy. Výsledkem je, že existuje o jednu rovnici méně;
4. Předchozí kroky opakujeme maximálně nkrát, kde n je počet rovnic v soustavě. Pokaždé vybereme pro „zpracování“ novou proměnnou. Pokud vzniknou nekonzistentní rovnice (například 0 = 8), systém je nekonzistentní.

Výsledkem je, že po několika krocích získáme buď vyřešený systém (případně s volnými proměnnými), nebo nekonzistentní. Povolené systémy spadají do dvou případů:

1. Počet proměnných se rovná počtu rovnic. To znamená, že systém je definován;
2. Počet proměnných další číslo rovnic. Shromáždíme všechny volné proměnné vpravo - získáme vzorce pro povolené proměnné. Tyto vzorce jsou napsány v odpovědi.

To je vše! Soustava lineárních rovnic vyřešena! Jedná se o poměrně jednoduchý algoritmus a pro jeho zvládnutí nemusíte kontaktovat vyššího učitele matematiky. Podívejme se na příklad:

Úkol. Řešte soustavu rovnic:

Popis kroků:

1. Odečtěte první rovnici od druhé a třetí – dostaneme povolenou proměnnou x 1;
2. Druhou rovnici vynásobíme (−1), třetí vydělíme (−3) - dostaneme dvě rovnice, do kterých vstupuje proměnná x 2 s koeficientem 1;
3. Druhou rovnici přidáme k první a odečteme od třetí. Dostaneme povolenou proměnnou x 2 ;
4. Nakonec odečteme třetí rovnici od první – dostaneme povolenou proměnnou x 3;
5. Obdrželi jsme schválený systém, napište odpověď.

Obecné řešení simultánního systému lineárních rovnic je nový systém, ekvivalentní původnímu, ve kterém jsou všechny povolené proměnné vyjádřeny jako volné.

Kdy může být potřeba obecné řešení? Pokud musíte udělat méně kroků než k (k je počet rovnic). Nicméně důvody, proč proces končí v některém kroku l< k , может быть две:

1. Po l. kroku jsme získali soustavu, která neobsahuje rovnici s číslem (l + 1). Ve skutečnosti je to dobře, protože... autorizovaný systém je stále získán - dokonce o několik kroků dříve.
2. Po 1. kroku jsme dostali rovnici, ve které jsou všechny koeficienty proměnných rovny nule a volný koeficient je jiný než nula. Toto je protichůdná rovnice, a proto je systém nekonzistentní.

Je důležité pochopit, že vznik nekonzistentní rovnice pomocí Gaussovy metody je dostatečným základem pro nekonzistenci. Zároveň podotýkáme, že v důsledku l. kroku nemohou zůstat žádné triviální rovnice - všechny jsou přímo v procesu proškrtány.

Popis kroků:

1. Odečtěte první rovnici vynásobenou 4 od druhé. První rovnici také přidáme do třetí - dostaneme povolenou proměnnou x 1;
2. Odečtěte třetí rovnici vynásobenou 2 od druhé – dostaneme protichůdnou rovnici 0 = −5.

Systém je tedy nekonzistentní, protože byla objevena nekonzistentní rovnice.

Úkol. Prozkoumejte kompatibilitu a najděte obecné řešení systému:

Popis kroků:

1. První rovnici odečteme od druhé (po vynásobení dvěma) a třetí - dostaneme povolenou proměnnou x 1;
2. Odečtěte druhou rovnici od třetí. Protože všechny koeficienty v těchto rovnicích jsou stejné, třetí rovnice se stane triviální. Současně vynásobte druhou rovnici číslem (−1);
3. Od první rovnice odečteme druhou – dostaneme povolenou proměnnou x 2. Celý systém rovnic je nyní také vyřešen;
4. Protože proměnné x 3 a x 4 jsou volné, přesuneme je doprava, abychom vyjádřili povolené proměnné. Toto je odpověď.

Systém je tedy konzistentní a neurčitý, protože existují dvě povolené proměnné (x 1 a x 2) a dvě volné (x 3 a x 4).