Jak zjistit, zda má soustava rovnic řešení. Online kalkulačka

Řešení lineárních soustav algebraické rovnice(SLAE) je bezpochyby nejdůležitějším tématem kurzu lineární algebry. Velké množství problémy ze všech odvětví matematiky jsou redukovány na systémy řešení lineární rovnice. Tyto faktory vysvětlují důvod tohoto článku. Materiál článku je vybrán a strukturován tak, abyste s jeho pomocí mohli

• zvolit optimální metodu pro řešení vašeho systému lineárních algebraických rovnic,
• studovat teorii zvolené metody,
• vyřešte svůj systém lineárních rovnic zvážením podrobných řešení typických příkladů a problémů.

Stručný popis materiálu článku.

Nejprve uvedeme všechny potřebné definice, pojmy a zavedeme notaci.

Dále se budeme zabývat metodami řešení soustav lineárních algebraických rovnic, ve kterých je počet rovnic roven počtu neznámých proměnných a které mají jednoznačné řešení. Zaprvé se zaměříme na Cramerovu metodu, zadruhé si ukážeme maticovou metodu řešení takových soustav rovnic, zatřetí rozebereme Gaussovu metodu (metoda sekvenční eliminace neznámé proměnné). Pro upevnění teorie určitě vyřešíme několik SLAE různými způsoby.

Poté přejdeme k řešení soustav lineárních algebraických rovnic obecný pohled, ve kterém se počet rovnic neshoduje s počtem neznámých proměnných nebo je hlavní matice systému singulární. Pojďme formulovat Kronecker-Capelliho teorém, který nám umožňuje stanovit kompatibilitu SLAE. Analyzujme řešení systémů (jsou-li kompatibilní) pomocí konceptu minoritní báze matice. Zvážíme také Gaussovu metodu a podrobně popíšeme řešení příkladů.

Určitě se zastavíme u struktury obecného řešení homogenních a nehomogenních soustav lineárních algebraických rovnic. Uveďme koncept základního systému řešení a ukažme, jak psát společné rozhodnutí SLAE pomocí vektorů základního systému řešení. Pro lepší pochopení se podívejme na pár příkladů.

Na závěr budeme uvažovat o soustavách rovnic, které lze redukovat na lineární různé úkoly, při jejichž řešení vznikají SLAE.

Navigace na stránce.

Definice, pojmy, označení.

Budeme uvažovat soustavy p lineárních algebraických rovnic s n neznámými proměnnými (p se může rovnat n) tvaru

Neznámé proměnné - koeficienty (některé reálné popř komplexní čísla), - volné členy (také reálná nebo komplexní čísla).

Tato forma záznamu se nazývá SLAE koordinovat.

V matricový formulář zápis tohoto systému rovnic má tvar,
Kde - hlavní matice systému, - sloupcová matice neznámých proměnných, - sloupcová matice volných členů.

Přidáme-li k matici A jako (n+1)-tý sloupec matici-sloupec volných členů, dostaneme tzv. rozšířená matice soustav lineárních rovnic. Rozšířená matice je obvykle označena písmenem T a sloupec volných výrazů je oddělen svislou čarou od zbývajících sloupců, tj.

Řešení soustavy lineárních algebraických rovnic nazvaný množina hodnot neznámých proměnných, která mění všechny rovnice systému na identity. Maticová rovnice pro dané hodnoty neznámých proměnných se také stává identitou.

Pokud má soustava rovnic alespoň jedno řešení, pak se nazývá kloub.

Pokud soustava rovnic nemá řešení, pak se nazývá nespojující.

Pokud má SLAE jedinečné řešení, pak se nazývá určitý; pokud existuje více než jedno řešení, pak – nejistý.

Jsou-li volné členy všech rovnic soustavy rovny nule , pak je zavolán systém homogenní, v opačném případě - heterogenní.

Řešení elementárních soustav lineárních algebraických rovnic.

Pokud se počet rovnic systému rovná počtu neznámých proměnných a determinant jeho hlavní matice není roven nule, pak se takové SLAE budou nazývat základní. Takové soustavy rovnic mají jedinečné řešení a v případě homogenní systém všechny neznámé proměnné jsou nulové.

Takové SLAE jsme začali studovat na střední škole. Při jejich řešení jsme vzali jednu rovnici, vyjádřili jednu neznámou proměnnou jinými a dosadili ji do zbývajících rovnic, pak vzali další rovnici, vyjádřili další neznámou proměnnou a dosadili ji do jiných rovnic a tak dále. Nebo použili metodu sčítání, to znamená, že přidali dvě nebo více rovnic, aby odstranili nějaké neznámé proměnné. Těmito metodami se nebudeme podrobně zabývat, protože jde v podstatě o modifikace Gaussovy metody.

Hlavními metodami řešení elementárních soustav lineárních rovnic jsou Cramerova metoda, maticová metoda a Gaussova metoda. Pojďme je roztřídit.

Řešení soustav lineárních rovnic Cramerovou metodou.

Předpokládejme, že potřebujeme vyřešit soustavu lineárních algebraických rovnic

ve kterém je počet rovnic roven počtu neznámých proměnných a determinant hlavní matice systému je odlišný od nuly, tedy .

Nechť je determinant hlavní matice systému a - determinanty matic, které jsou získány z A nahrazením 1., 2., …, n sloupec respektive sloupec volných členů:

S tímto zápisem se neznámé proměnné počítají pomocí vzorců Cramerovy metody as . Takto je pomocí Cramerovy metody nalezeno řešení soustavy lineárních algebraických rovnic.

Příklad.

Cramerova metoda .

Řešení.

Hlavní matice systému má tvar . Vypočítejme jeho determinant (pokud je to nutné, viz článek):

Protože determinant hlavní matice systému je nenulový, má systém jedinečné řešení, které lze nalézt Cramerovou metodou.

Pojďme si složit a vypočítat potřebné determinanty (determinant získáme nahrazením prvního sloupce v matici A sloupcem volných členů, determinant nahrazením druhého sloupce sloupcem volných členů a nahrazením třetího sloupce matice A sloupcem volných členů) :

Hledání neznámých proměnných pomocí vzorců :

Odpovědět:

Hlavní nevýhodou Cramerovy metody (pokud ji lze nazvat nevýhodou) je složitost výpočtu determinantů při počtu rovnic v soustavě větším než tři.

Řešení soustav lineárních algebraických rovnic maticovou metodou (pomocí inverzní matice).

Nechť je dán systém lineárních algebraických rovnic v maticovém tvaru, kde matice A má rozměr n x n a její determinant je nenulový.

Protože je matice A invertibilní, to znamená, že existuje inverzní matice. Pokud obě strany rovnosti vynásobíme levou, dostaneme vzorec pro nalezení matice-sloupce neznámých proměnných. Takto jsme získali řešení soustavy lineárních algebraických rovnic maticová metoda.

Příklad.

Řešení soustavy lineárních rovnic maticová metoda.

Řešení.

Přepišme soustavu rovnic do maticového tvaru:

Protože

pak lze SLAE vyřešit pomocí maticové metody. Používáním inverzní maticeřešení tohoto systému lze nalézt jako .

Sestrojme inverzní matici pomocí matice z algebraické sčítání prvky matice A (pokud je to nutné, viz článek):

Zbývá vypočítat matici neznámých proměnných vynásobením inverzní matice do maticového sloupce volných členů (v případě potřeby viz článek):

Odpovědět:

nebo v jiném zápisu x 1 = 4, x 2 = 0, x 3 = -1.

Hlavním problémem při hledání řešení soustav lineárních algebraických rovnic maticovou metodou je složitost hledání inverzní matice, zejména pro čtvercové matice vyššího než třetího řádu.

Řešení soustav lineárních rovnic Gaussovou metodou.

Předpokládejme, že potřebujeme najít řešení systému n lineárních rovnic s n neznámými proměnnými
determinant hlavní matice je odlišný od nuly.

Podstata Gaussovy metody spočívá v postupném odstraňování neznámých proměnných: nejprve je x 1 vyloučeno ze všech rovnic systému, počínaje druhou, pak je x 2 vyloučeno ze všech rovnic, počínaje třetí, a tak dále, dokud nezůstane pouze neznámá proměnná x n v poslední rovnici. Tento proces transformace systémových rovnic k postupné eliminaci neznámých proměnných se nazývá přímou Gaussovou metodou. Po dokončení tah vpřed pomocí Gaussovy metody se z poslední rovnice zjistí x n, pomocí této hodnoty se z předposlední rovnice vypočítá x n-1 a tak dále se z první rovnice zjistí x 1. Proces výpočtu neznámých proměnných při přechodu od poslední rovnice systému k první se nazývá inverzní ke Gaussově metodě.

Pojďme si stručně popsat algoritmus pro eliminaci neznámých proměnných.

Budeme předpokládat, že , protože toho můžeme vždy dosáhnout přeskupením rovnic soustavy. Vynechme neznámou proměnnou x 1 ze všech rovnic soustavy, počínaje druhou. Abychom to udělali, ke druhé rovnici soustavy přidáme první, vynásobenou , ke třetí rovnici přidáme první, vynásobenou a tak dále, k n-té rovnici přidáme první, vynásobenou . Systém rovnic po takových transformacích nabude tvaru

kde a .

Ke stejnému výsledku bychom dospěli, kdybychom x 1 vyjádřili pomocí jiných neznámých proměnných v první rovnici soustavy a výsledný výraz dosadili do všech ostatních rovnic. Proměnná x 1 je tedy vyloučena ze všech rovnic, počínaje druhou.

Dále postupujeme obdobně, ale pouze s částí výsledné soustavy, která je vyznačena na obrázku

Abychom to udělali, ke třetí rovnici soustavy přidáme druhou, vynásobenou , ke čtvrté rovnici přidáme druhou, vynásobenou , atd., k n-té rovnici přidáme druhou, vynásobenou . Systém rovnic po takových transformacích nabude tvaru

kde a . Proměnná x 2 je tedy vyloučena ze všech rovnic, počínaje třetí.

Dále přistoupíme k eliminaci neznámého x 3, přičemž obdobně postupujeme s částí systému vyznačenou na obrázku

Pokračujeme tedy v přímém postupu Gaussovy metody, dokud systém nezíská formu

Od této chvíle začínáme zpětný zdvih Gaussova metoda: z poslední rovnice vypočítáme x n jako , pomocí získané hodnoty x n zjistíme x n-1 z předposlední rovnice a tak dále, z první rovnice zjistíme x 1.

Příklad.

Řešení soustavy lineárních rovnic Gaussova metoda.

Řešení.

Vynechme neznámou proměnnou x 1 z druhé a třetí rovnice soustavy. Za tímto účelem k oběma stranám druhé a třetí rovnice přidáme odpovídající části první rovnice, vynásobené a respektive:

Nyní odstraníme x 2 ze třetí rovnice tak, že k její levé a pravé straně přidáme levou a pravou stranu druhé rovnice, vynásobíme:

Tím je dopředný zdvih Gaussovy metody dokončen, začínáme zpětný zdvih.

Z poslední rovnice výsledné soustavy rovnic zjistíme x 3:

Z druhé rovnice dostaneme .

Z první rovnice najdeme zbývající neznámou proměnnou a tím dokončíme opak Gaussovy metody.

Odpovědět:

Xi = 4, x 2 = 0, x 3 = -1.

Řešení soustav lineárních algebraických rovnic obecného tvaru.

V obecný případ počet rovnic soustavy p se neshoduje s počtem neznámých proměnných n:

Takové SLAE nemusí mít žádná řešení, mít jediné řešení nebo mít nekonečně mnoho řešení. Toto tvrzení platí také pro soustavy rovnic, jejichž hlavní matice je čtvercová a singulární.

Kroneckerova-Capelliho věta.

Před nalezením řešení soustavy lineárních rovnic je nutné zjistit její kompatibilitu. Odpověď na otázku, kdy je SLAE kompatibilní a kdy nekonzistentní, dává Kroneckerova-Capelliho věta:
Aby soustava p rovnic s n neznámými (p se může rovnat n) byla konzistentní, je nutné a postačující, aby hodnost hlavní matice soustavy byla rovna hodnosti rozšířené matice, tzn. , Pořadí (A) = Pořadí (T).

Uvažujme jako příklad aplikaci Kronecker-Capelliho věty pro určení kompatibility soustavy lineárních rovnic.

Příklad.

Zjistěte, zda má soustava lineárních rovnic řešení.

Řešení.

. Použijme metodu ohraničení nezletilých. Minor druhého řádu odlišný od nuly. Podívejme se na nezletilé třetího řádu, kteří s tím sousedí:

Protože všechny hraničící nezletilé třetího řádu jsou rovny nule, hodnost hlavní matice se rovná dvěma.

Na druhé straně hodnost rozšířené matice se rovná třem, protože menší je třetího řádu

odlišný od nuly.

Tím pádem, Rang(A) tedy s použitím Kronecker-Capelliho věty můžeme dojít k závěru, že původní systém lineárních rovnic je nekonzistentní.

Odpovědět:

Systém nemá řešení.

Naučili jsme se tedy stanovit nekonzistenci systému pomocí Kronecker-Capelliho teorému.

Ale jak najít řešení pro SLAE, pokud je prokázána jeho kompatibilita?

K tomu potřebujeme koncept minoritní báze matice a větu o hodnosti matice.

Méně důležitý nejvyššího řádu nazývá se matice A odlišná od nuly základní.

Z definice základu minor vyplývá, že jeho pořadí se rovná hodnosti matice. Pro nenulovou matici A může být několik základů minor, vždy je jeden základ minor.

Vezměme si například matici .

Všechny minoritní hodnoty třetího řádu této matice jsou rovny nule, protože prvky třetího řádku této matice jsou součtem odpovídajících prvků prvního a druhého řádku.

Následující nezletilí druhého řádu jsou základní, protože jsou nenulové

Nezletilí nejsou základní, protože se rovnají nule.

Věta o hodnosti matice.

Je-li hodnost matice řádu p x n rovna r, pak všechny řádkové (a sloupcové) prvky matice, které netvoří zvolený základ minor, jsou lineárně vyjádřeny pomocí odpovídajících řádkových (a sloupcových) prvků tvořících základ minor.

Co nám říká teorém o hodnosti matice?

Pokud jsme podle Kronecker-Capelliho věty stanovili kompatibilitu systému, pak zvolíme libovolnou menší bázu hlavní matice systému (její řád je roven r) a vyloučíme ze systému všechny rovnice, které netvoří vybraný základ moll. Takto získaný SLAE bude ekvivalentní původnímu, protože vyřazené rovnice jsou stále nadbytečné (podle teorému o pořadí matice jsou lineární kombinací zbývajících rovnic).

V důsledku toho jsou po vyřazení nepotřebných rovnic systému možné dva případy.

Pokud je počet rovnic r ve výsledné soustavě roven počtu neznámých proměnných, pak bude definitivní a jediné řešení lze nalézt Cramerovou metodou, maticovou metodou nebo Gaussovou metodou.

Příklad.

.

Řešení.

Hodnost hlavní matice systému se rovná dvěma, protože menší je druhého řádu odlišný od nuly. Rozšířená hodnost Matrix se také rovná dvěma, protože jediný minor třetího řádu je nula

a výše zmíněný moll druhého řádu se liší od nuly. Na základě Kronecker-Capelliho teorému můžeme tvrdit kompatibilitu původního systému lineárních rovnic, protože Rank(A)=Rank(T)=2.

Jako základ menší bereme . Je tvořena koeficienty první a druhé rovnice:


Třetí rovnice soustavy se nepodílí na tvorbě báze minor, proto ji ze soustavy na základě věty o hodnosti matice vyloučíme:


Takto jsme získali elementární systém lineárních algebraických rovnic. Pojďme to vyřešit pomocí Cramerovy metody:


Odpovědět:

x 1 = 1, x 2 = 2.

Pokud je počet rovnic r ve výsledném SLAE menší než počet neznámých proměnných n, pak na levých stranách rovnic ponecháme členy tvořící základ menší a zbývající členy přeneseme na pravé strany rovnice. rovnice soustavy s opačným znaménkem.

Neznámé proměnné (z nich r), které zůstávají na levé straně rovnic, se nazývají hlavní.

Volají se neznámé proměnné (existuje n - r kusů), které jsou na pravé straně volný, uvolnit.

Nyní věříme, že volné neznámé proměnné mohou nabývat libovolných hodnot, zatímco r hlavních neznámých proměnných bude vyjádřeno prostřednictvím volných neznámých proměnných jedinečným způsobem. Jejich vyjádření lze nalézt řešením výsledného SLAE pomocí Cramerovy metody, maticové metody nebo Gaussovy metody.

Podívejme se na to na příkladu.

Příklad.

Řešte soustavu lineárních algebraických rovnic .

Řešení.

Pojďme najít hodnost hlavní matice systému metodou ohraničení nezletilých. Vezměme a 1 1 = 1 jako nenulovou moll prvního řádu. Začněme hledat nenulovou moll druhého řádu hraničící s touto moll:


Takto jsme našli nenulovou moll druhého řádu. Začněme hledat nenulovou hraniční moll třetího řádu:


Hodnost hlavní matice je tedy tři. Hodnost rozšířené matice je také rovna třem, to znamená, že systém je konzistentní.

Za základ bereme nalezený nenulový moll třetího řádu.

Pro názornost uvádíme prvky, které tvoří základ moll:


Ponecháme členy obsažené v základu moll na levé straně rovnic soustavy a zbytek přeneseme z opačné znaky na pravé strany:


Volným neznámým proměnným x 2 a x 5 dáme libovolné hodnoty, tedy akceptujeme , kde jsou libovolná čísla. V tomto případě bude mít SLAE formu


Vyřešme výsledný elementární systém lineárních algebraických rovnic Cramerovou metodou:


Proto, .

V odpovědi nezapomeňte uvést volné neznámé proměnné.

Odpovědět:

Kde jsou libovolná čísla.

Shrnout.

Při řešení systému obecných lineárních algebraických rovnic nejprve určíme jeho kompatibilitu pomocí Kronecker-Capelliho věty. Pokud se hodnost hlavní matice nerovná hodnosti rozšířené matice, docházíme k závěru, že systém je nekompatibilní.

Pokud se hodnost hlavní matice rovná hodnosti rozšířené matice, vybereme základ menší a zahodíme rovnice systému, které se nepodílejí na tvorbě vybrané základny vedlejší.

Pokud je řád menšího základu roven počtu neznámých proměnných, pak má SLAE jedinečné řešení, které lze nalézt jakoukoli nám známou metodou.

Pokud je řád menšího základu menší než počet neznámých proměnných, pak na levé straně systémových rovnic ponecháme členy s hlavními neznámými proměnnými, převedeme zbývající členy na pravé strany a dáme libovolné hodnoty volné neznámé proměnné. Z výsledné soustavy lineárních rovnic najdeme hlavní neznámé proměnné pomocí Cramerovy metody, maticové metody nebo Gaussovy metody.

Gaussova metoda pro řešení soustav lineárních algebraických rovnic obecného tvaru.

Gaussovu metodu lze použít k řešení systémů lineárních algebraických rovnic jakéhokoli druhu, aniž by bylo nutné nejprve testovat jejich konzistenci. Proces sekvenční eliminace neznámých proměnných umožňuje učinit závěr o kompatibilitě i nekompatibilitě SLAE, a pokud existuje řešení, umožňuje jej najít.

Z výpočetního hlediska je výhodnější Gaussova metoda.

Bacha Detailní popis a analyzoval příklady v článku Gaussova metoda pro řešení soustav lineárních algebraických rovnic obecného tvaru.

Zápis obecného řešení homogenních a nehomogenních lineárních algebraických systémů pomocí vektorů základního systému řešení.

V této části promluvime si o simultánních homogenních a nehomogenních soustavách lineárních algebraických rovnic s nekonečným počtem řešení.

Pojďme se nejprve zabývat homogenními systémy.

Základní systém řešení homogenní soustava p lineárních algebraických rovnic s n neznámými proměnnými je sbírka (n – r) lineárně nezávislých řešení této soustavy, kde r je řád menší báze hlavní matice soustavy.

Označíme-li lineárně nezávislá řešení homogenní SLAE jako X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) jsou sloupcové matice dimenze n o 1) , pak je obecné řešení tohoto homogenního systému reprezentováno jako lineární kombinace vektorů fundamentálního systému řešení s libovolnými konstantními koeficienty C 1, C 2, ..., C (n-r), tedy .

Co znamená pojem obecné řešení homogenní soustavy lineárních algebraických rovnic (oroslau)?

Význam je jednoduchý: vzorec nastavuje vše možné řešení původní SLAE, jinými slovy, vezmeme-li libovolnou množinu hodnot libovolných konstant C 1, C 2, ..., C (n-r), podle vzorce získáme jedno z řešení původního homogenního SLAE.

Pokud tedy najdeme fundamentální systém řešení, můžeme všechna řešení tohoto homogenního SLAE definovat jako .

Ukažme si proces konstrukce základního systému řešení homogenního SLAE.

Z původní soustavy lineárních rovnic vybereme minoritní báze, vyloučíme ze soustavy všechny ostatní rovnice a všechny členy obsahující volné neznámé proměnné přeneseme na pravé strany soustav rovnic s opačnými znaménky. Dejme zdarma neznámé proměnné hodnoty 1,0,0,…,0 a vypočítat hlavní neznámé řešením výsledné elementární soustavy lineárních rovnic libovolným způsobem, např. Cramerovou metodou. Výsledkem bude X (1) - první řešení základního systému. Pokud dáte zdarma neznámé hodnoty 0,1,0,0,…,0 a spočteme hlavní neznámé, dostaneme X (2) . A tak dále. Pokud volným neznámým proměnným přiřadíme hodnoty 0,0,…,0,1 a vypočteme hlavní neznámé, dostaneme X (n-r) . Tímto způsobem bude sestaven základní systém řešení homogenního SLAE a jeho obecné řešení lze zapsat ve tvaru .

Pro nehomogenní systémy lineárních algebraických rovnic je obecné řešení reprezentováno ve tvaru , kde je obecné řešení odpovídajícího homogenního systému a je partikulárním řešením původního nehomogenního SLAE, které získáme tak, že volným neznámým dáme hodnoty ​​0,0,...,0 a výpočet hodnot hlavních neznámých.

Podívejme se na příklady.

Příklad.

Najděte základní soustavu řešení a obecné řešení homogenní soustavy lineárních algebraických rovnic .

Řešení.

Hodnost hlavní matice homogenních soustav lineárních rovnic je vždy rovna hodnosti rozšířené matice. Pomocí metody ohraničení nezletilých najdeme hodnost hlavní matice. Jako nenulový moll prvního řádu vezmeme prvek a 1 1 = 9 hlavní matice systému. Pojďme najít hraniční nenulovou moll druhého řádu:

Byl nalezen moll druhého řádu, odlišný od nuly. Pojďme si projít nezletilé třetího řádu, které s ním sousedí, a hledat nenulovou jedničku:

Všichni hraniční nezletilí třetího řádu se rovnají nule, proto se hodnost hlavní a rozšířené matice rovná dvěma. Pojďme vzít . Pro přehlednost si všimněme prvků systému, které jej tvoří:

Třetí rovnice původního SLAE se nepodílí na tvorbě základu moll, proto ji lze vyloučit:

Členy obsahující hlavní neznámé ponecháme na pravých stranách rovnic a členy s volnými neznámými přeneseme na pravé strany:

Sestavme základní soustavu řešení původní homogenní soustavy lineárních rovnic. Základní systém řešení tohoto SLAE se skládá ze dvou řešení, protože původní SLAE obsahuje čtyři neznámé proměnné a řád jeho základny minor je roven dvěma. Abychom našli X (1), dáme volným neznámým proměnným hodnoty x 2 = 1, x 4 = 0, pak najdeme hlavní neznámé ze soustavy rovnic
.

§1. Soustavy lineárních rovnic.

Zobrazit systém

nazývaný systém m lineární rovnice s n neznámý.

Tady
- neznámý, - koeficienty pro neznámé,
- volné členy rovnic.

Pokud jsou všechny volné členy rovnic rovny nule, systém se nazývá homogenní.Rozhodnutím systém se nazývá sbírka čísel
, při jejich dosazení do systému místo neznámých se všechny rovnice promění v identity. Systém se nazývá kloub, pokud má alespoň jedno řešení. Kompatibilní systém, který má jedinečné řešení, se nazývá určitý. Tyto dva systémy se nazývají ekvivalent, pokud se množiny jejich řešení shodují.

Systém (1) může být reprezentován v maticové formě pomocí rovnice

(2)

.

§2. Kompatibilita soustav lineárních rovnic.

Nazvěme rozšířenou matici systému (1) maticí

Kronecker-Capelliho věta. Systém (1) je konzistentní tehdy a pouze tehdy, když se hodnost systémové matice rovná hodnosti rozšířené matice:

.

§3. Systémové řešenín lineární rovnice sn neznámý.

Uvažujme nehomogenní systém n lineární rovnice s n neznámý:

(3)

Cramerův teorém.Pokud je hlavní determinant systému (3)
, pak má systém jedinečné řešení určené vzorcem:

těch.
,

Kde - determinant získaný z determinantu výměna, nahrazení sloupec do sloupce volných členů.

Li
a alespoň jeden z nich ≠0, pak systém nemá žádná řešení.

Li
, pak má systém nekonečně mnoho řešení.

Systém (3) lze řešit pomocí jeho maticového tvaru (2). Pokud je matice hodnost A rovná se n, tj.
, pak matice A má inverzní
. Násobení maticové rovnice
do matice
vlevo dostaneme:

.

Poslední rovnost vyjadřuje způsob řešení soustav lineárních rovnic pomocí inverzní matice.

Příklad.Řešte soustavu rovnic pomocí inverzní matice.

Řešení. Matice
nedegenerované, od
, což znamená, že existuje inverzní matice. Pojďme vypočítat inverzní matici:
.

,

Cvičení. Systém řešte Cramerovou metodou.

§4. Řešení libovolných soustav lineárních rovnic.

Nechť je dána nehomogenní soustava lineárních rovnic tvaru (1).

Předpokládejme, že systém je konzistentní, tzn. podmínka Kronecker-Capelliho věty je splněna:
. Pokud je matice hodnost
(počet neznámých), pak má systém unikátní řešení. Li
, pak má systém nekonečně mnoho řešení. Nech mě to vysvětlit.

Nechť hodnost matice r(A)= r< n. Protože
, pak je tam nějaký nenulový moll řádu r. Říkejme tomu základní moll. Neznámé, jejichž koeficienty tvoří menší základ, budeme nazývat základní proměnné. Zbývající neznámé nazýváme volné proměnné. Přeuspořádejme rovnice a přečíslujeme proměnné tak, aby tato vedlejší byla umístěna v levém horním rohu systémové matice:

.

První rčáry jsou lineárně nezávislé, zbytek je vyjádřen jejich prostřednictvím. Proto lze tyto řádky (rovnice) zahodit. Dostaneme:

Dejme volným proměnným libovolné číselné hodnoty: . Ponechme pouze základní proměnné na levé straně a volné přesuneme na pravou stranu.

Mám systém r lineární rovnice s r neznámý, jehož determinant je odlišný od 0. Má jedinečné řešení.

Tato soustava se nazývá obecné řešení soustavy lineárních rovnic (1). Jinak: nazývá se vyjádření základních proměnných prostřednictvím volných obecné rozhodnutí systémy. Z toho můžete získat nekonečné množství soukromá řešení, dává volným proměnným libovolné hodnoty. Zavolá se konkrétní řešení získané z obecného pro nulové hodnoty volných proměnných základní řešení. Počet různých základních řešení nepřesahuje
. Volá se základní řešení s nezápornými složkami vedlejší systémové řešení.

Příklad.

,r=2.

Proměnné
- základní,
- volný, uvolnit.

Sečteme rovnice; pojďme se vyjádřit
přes
:

- společné rozhodnutí.

- soukromé řešení pro
.

- základní řešení, reference.

§5. Gaussova metoda.

Gaussova metoda je univerzální metodou pro studium a řešení libovolných soustav lineárních rovnic. Spočívá v redukci systému na diagonální (nebo trojúhelníkovou) formu postupným odstraňováním neznámých pomocí elementárních transformací, které neporušují ekvivalenci systémů. Proměnná se považuje za vyloučenou, pokud je obsažena pouze v jedné rovnici systému s koeficientem 1.

Elementární transformace systémy jsou:

Násobení rovnice číslem jiným než nula;

Přidání rovnice vynásobené libovolným číslem jinou rovnicí;

Přeskupení rovnic;

Odmítnutí rovnice 0 = 0.

Elementární transformace lze provádět nikoli na rovnicích, ale na rozšířených maticích výsledných ekvivalentních systémů.

Příklad.

Řešení. Zapišme si rozšířenou matici systému:

.

Provedením elementárních transformací zredukujeme levou stranu matice na jednotkový tvar: na hlavní diagonále vytvoříme jedničky a mimo ni nuly.

Komentář. Jestliže při provádění elementárních transformací získáme rovnici tvaru 0 = k(Kde Na0), pak je systém nekonzistentní.

Řešení soustav lineárních rovnic metodou sekvenční eliminace neznámých lze zapsat ve tvaru tabulky.

Levý sloupec tabulky obsahuje informace o vyloučených (základních) proměnných. Zbývající sloupce obsahují koeficienty neznámých a volné členy rovnic.

Rozšířená matice systému je zaznamenána ve zdrojové tabulce. Dále začneme provádět Jordanovy transformace:

1. Vyberte proměnnou , který se stane základem. Odpovídající sloupec se nazývá klíčový sloupec. Vyberte rovnici, ve které tato proměnná zůstane a bude vyloučena z ostatních rovnic. Odpovídající řádek tabulky se nazývá klíčový řádek. Součinitel , stojící na průsečíku klíčové řady a klíčového sloupce, se nazývá klíč.

2. Prvky klíčového řetězce jsou rozděleny na klíčový prvek.

3. Klíčový sloupec je vyplněn nulami.

4. Zbývající prvky se vypočítají pomocí pravidla obdélníku. Sestavte obdélník, na jehož protilehlých vrcholech je klíčový prvek a přepočítaný prvek; od součinu prvků umístěných na diagonále obdélníku s klíčovým prvkem se odečte součin prvků druhé diagonály a výsledný rozdíl se vydělí klíčovým prvkem.

Příklad. Najděte obecné řešení a základní řešení soustavy rovnic:

Řešení.

Obecné řešení systému:

Základní řešení:
.

Jediná substituční transformace umožňuje přejít z jedné báze systému na druhou: místo jedné z hlavních proměnných je do báze zavedena jedna z volných proměnných. Chcete-li to provést, vyberte klíčový prvek ve sloupci volné proměnné a proveďte transformace podle výše uvedeného algoritmu.

§6. Hledání řešení podpory

Referenční řešení soustavy lineárních rovnic je základní řešení, které neobsahuje záporné složky.

Referenční řešení soustavy se nalézají Gaussovou metodou při splnění následujících podmínek.

1. V původním systému musí být všechny volné termíny nezáporné:
.

2. Klíčový prvek je vybrán z kladných koeficientů.

3. Má-li proměnná zavedená do báze několik kladných koeficientů, pak klíčová linie je ta, ve které je poměr volného členu ke kladnému koeficientu nejmenší.

Poznámka 1. Pokud se v procesu eliminace neznámých objeví rovnice, ve které jsou všechny koeficienty kladné a volný člen
, pak systém nemá žádná nezáporná řešení.

Poznámka 2. Pokud ve sloupcích koeficientů pro volné proměnné není jediný kladný prvek, není přechod na jiné referenční řešení možný.

Příklad.

V praxi jsou však rozšířeny další dva případy:

– Systém je nekonzistentní (nemá žádná řešení);
– Systém je konzistentní a má nekonečně mnoho řešení.

Poznámka : Termín „konzistence“ znamená, že systém má alespoň nějaké řešení. U řady problémů je nutné nejprve prověřit kompatibilitu systému, jak na to, viz článek o hodnost matrik.

Pro tyto systémy se používá nejuniverzálnější ze všech způsobů řešení - Gaussova metoda. Ve skutečnosti k odpovědi povede také „školní“ metoda, ale ve vyšší matematice je zvykem používat Gaussovu metodu postupného odstraňování neznámých. Ti, kteří nejsou obeznámeni s algoritmem Gaussovy metody, si prosím nejprve prostudujte lekci Gaussova metoda pro figuríny.

Samotné transformace elementární matice jsou naprosto stejné, rozdíl bude v zakončení řešení. Nejprve se podívejme na pár příkladů, kdy systém nemá žádná řešení (nekonzistentní).

Příklad 1

Co vás na tomto systému okamžitě upoutá? Počet rovnic je menší než počet proměnných. Pokud je počet rovnic menší než počet proměnných, pak můžeme rovnou říci, že systém je buď nekonzistentní, nebo má nekonečně mnoho řešení. A nezbývá než to zjistit.

Začátek řešení je úplně obyčejný - zapíšeme rozšířenou matici soustavy a pomocí elementárních transformací ji uvedeme do stupňovité podoby:

(1) V levém horním kroku potřebujeme získat +1 nebo –1. V prvním sloupci žádná taková čísla nejsou, takže přeskupení řádků nic nedá. Jednotka se bude muset organizovat sama, a to lze provést několika způsoby. Udělal jsem toto: K prvnímu řádku přidáme třetí řádek, vynásobený –1.

(2) Nyní dostaneme dvě nuly v prvním sloupci. Ke druhému řádku přidáme první řádek vynásobený 3. Ke třetímu řádku přidáme první řádek vynásobený 5.

(3) Po dokončení transformace je vždy vhodné podívat se, zda je možné výsledné řetězce zjednodušit? Umět. Druhý řádek vydělíme 2 a zároveň získáme požadovanou –1 na druhém kroku. Vydělte třetí řádek číslem –3.

(4) Přidejte druhý řádek ke třetímu řádku.

Pravděpodobně každý si všiml špatné linie, která vyplynula z elementárních transformací: . Je jasné, že to tak být nemůže. Přepišme výslednou matici zpět k soustavě lineárních rovnic:

Pokud se v důsledku elementárních transformací získá řetězec tvaru, kde je číslo jiné než nula, pak je systém nekonzistentní (nemá řešení).

Jak zapsat konec úkolu? Nakreslime bílou křídou: „jako výsledek elementárních transformací se získá řetězec tvaru , kde “ a dáme odpověď: systém nemá řešení (nekonzistentní).

Pokud je podle podmínky požadováno ZKOUMAT kompatibilitu systému, pak je nutné formalizovat řešení v pevnějším stylu pomocí konceptu hodnost matice a Kronecker-Capelliho teorém.

Vezměte prosím na vědomí, že zde nedochází k žádnému obrácení Gaussova algoritmu – neexistují žádná řešení a jednoduše není co najít.

Příklad 2

Řešte soustavu lineárních rovnic

Toto je příklad pro nezávislé rozhodnutí. Kompletní řešení a odpověď na konci lekce. Znovu vám připomínám, že vaše řešení se může lišit od mého řešení, Gaussův algoritmus nemá silnou „rigiditu“.

Další technická vlastnost řešení: elementární transformace lze zastavit Najednou, jakmile řádek jako , kde . Uvažujme podmíněný příklad: předpokládejme, že po první transformaci je získána matice . Matice ještě nebyla zredukována na echelonovou formu, ale není potřeba dalších elementárních transformací, protože se objevila linie formy, kde . Okamžitě je třeba odpovědět, že systém je nekompatibilní.

Když systém lineárních rovnic nemá řešení, je to téměř dar, protože se získá krátké řešení, někdy doslova ve 2-3 krocích.

Ale všechno na tomto světě je vyvážené a problém, ve kterém má systém nekonečně mnoho řešení, je prostě delší.

Příklad 3

Řešte soustavu lineárních rovnic

Existují 4 rovnice a 4 neznámé, takže systém může mít buď jediné řešení, nebo nemá řešení, nebo může mít nekonečně mnoho řešení. Ať je to jak chce, Gaussova metoda nás v každém případě dovede k odpovědi. To je jeho všestrannost.

Začátek je opět standardní. Zapišme si rozšířenou matici systému a pomocí elementárních transformací ji uveďme do stupňovité podoby:

To je vše a báli jste se.

(1) Vezměte prosím na vědomí, že všechna čísla v prvním sloupci jsou dělitelná 2, takže 2 je v kroku vlevo nahoře v pořádku. Ke druhému řádku přidáme první řádek, vynásobený –4. Ke třetímu řádku přidáme první řádek, vynásobený –2. Ke čtvrtému řádku přidáme první řádek, vynásobený –1.

Pozornost! Mnohé může zlákat čtvrtý řádek odčítat první řada. To lze provést, ale není to nutné, zkušenost ukazuje, že pravděpodobnost chyby ve výpočtech se několikanásobně zvyšuje. Stačí přidat: Ke čtvrtému řádku přidejte první řádek vynásobený –1 – přesně tak!

(2) Poslední tři řádky jsou poměrné, dva z nich lze smazat.

Zde musíme znovu ukázat zvýšená pozornost, ale jsou čáry skutečně proporcionální? Pro jistotu (zejména u čajové konvice) by bylo dobré vynásobit druhý řádek číslem –1 a čtvrtý řádek vydělit dvěma, čímž vzniknou tři stejné řádky. A teprve potom odstranit dva z nich.

V důsledku elementárních transformací je rozšířená matice systému redukována na stupňovitý tvar:

Při psaní úkolu do sešitu je vhodné si pro názornost dělat stejné poznámky tužkou.

Přepišme odpovídající soustavu rovnic:

Zde není cítit „obyčejné“ jediné řešení systému. Neexistuje ani špatná linie. To znamená, že jde o třetí zbývající případ – systém má nekonečně mnoho řešení. Někdy je podle podmínky potřeba prozkoumat kompatibilitu systému (tedy dokázat, že nějaké řešení vůbec existuje), o tom se dočtete v posledním odstavci článku Jak zjistit hodnost matice? Ale teď pojďme na základy:

Nekonečná množina řešení soustavy je stručně zapsána ve formě tzv obecné řešení systému .

Obecné řešení soustavy najdeme pomocí inverze Gaussovy metody.

Nejprve musíme definovat, jaké proměnné máme základní a jaké proměnné volný, uvolnit. Nemusíte se obtěžovat pojmy lineární algebry, jen si pamatujte, že takové existují základní proměnné A volné proměnné.

Základní proměnné vždy „sedí“ striktně na stupních matice.
V tomto příkladu jsou základní proměnné a

Volné proměnné jsou vším zbývající proměnné, které nedostaly krok. V našem případě jsou dvě: – volné proměnné.

Nyní potřebujete Všechno základní proměnné vyjádřit pouze skrz volné proměnné.

Opačná strana Gaussova algoritmu tradičně funguje zdola nahoru.
Z druhé rovnice soustavy vyjádříme základní proměnnou:

Nyní se podívejte na první rovnici: . Nejprve do něj dosadíme nalezený výraz:

Zbývá vyjádřit základní proměnnou pomocí volných proměnných:

Nakonec jsme dostali, co jsme potřebovali - Všechno jsou vyjádřeny základní proměnné ( a ). pouze skrz volné proměnné:

Ve skutečnosti je obecné řešení připraveno:

Jak správně napsat obecné řešení?
Volné proměnné se do obecného řešení zapisují „sami“ a striktně na svá místa. V v tomto případě volné proměnné by měly být zapsány na druhé a čtvrté pozici:
.

Výsledné výrazy pro základní proměnné a samozřejmě musí být napsáno na první a třetí pozici:

Poskytování volných proměnných libovolné hodnoty, najdete jich nekonečně mnoho soukromá řešení. Nejoblíbenějšími hodnotami jsou nuly, protože konkrétní řešení je nejjednodušší získat. Dosadíme do obecného řešení:

– soukromé řešení.

Další sladká dvojice jsou jedničky, dosadíme je do obecného řešení:

– další soukromé řešení.

Je snadné vidět, že systém rovnic má nekonečně mnoho řešení(protože můžeme dát volné proměnné žádný hodnoty)

Každý konkrétní řešení musí splňovat ke každému rovnice systému. To je základ pro „rychlou“ kontrolu správnosti řešení. Vezměte si například konkrétní řešení a dosaďte ho na levou stranu každé rovnice původního systému:

Všechno se musí sejít. A s jakýmkoli konkrétním řešením, které obdržíte, by také mělo vše souhlasit.

Ale přísně vzato je kontrola konkrétního řešení někdy klamavá, tzn. nějaké konkrétní řešení může vyhovět každé rovnici systému, ale samotné obecné řešení je ve skutečnosti nalezeno nesprávně.

Proto je ověření obecného řešení důkladnější a spolehlivější. Jak zkontrolovat výsledné obecné řešení ?

Není to těžké, ale docela zdlouhavé. Musíme přijmout výrazy základní proměnné, v tomto případě a , a dosaďte je na levou stranu každé rovnice systému.

Na levou stranu první rovnice soustavy:

Na levou stranu druhé rovnice soustavy:


Získá se pravá strana původní rovnice.

Příklad 4

Soustavu řešte Gaussovou metodou. Najděte obecné řešení a dvě konkrétní. Zkontrolujte obecné řešení.

Toto je příklad, který můžete vyřešit sami. Zde je mimochodem opět počet rovnic menší než počet neznámých, což znamená, že je okamžitě jasné, že systém bude buď nekonzistentní, nebo bude mít nekonečný počet řešení. Co je důležité v samotném rozhodovacím procesu? Pozor a ještě jednou pozornost. Úplné řešení a odpověď na konci lekce.

A pár dalších příkladů pro posílení materiálu

Příklad 5

Řešte soustavu lineárních rovnic. Pokud má systém nekonečně mnoho řešení, najděte dvě konkrétní řešení a zkontrolujte obecné řešení

Řešení: Zapišme si rozšířenou matici systému a pomocí elementárních transformací ji uveďme do stupňovité podoby:

(1) Přidejte první řádek k druhému řádku. Ke třetímu řádku přidáme první řádek vynásobený 2. Ke čtvrtému řádku přidáme první řádek vynásobený 3.
(2) Ke třetímu řádku přidáme druhý řádek, vynásobený –5. Ke čtvrtému řádku přidáme druhý řádek, vynásobený –7.
(3) Třetí a čtvrtý řádek jsou stejné, jeden z nich smažeme.

Tohle je taková nádhera:

Základní proměnné sedí na stupních, tedy - základní proměnné.
Existuje pouze jedna volná proměnná, která nezískala krok:

Zvrátit:
Vyjádřeme základní proměnné pomocí volné proměnné:
Ze třetí rovnice:

Uvažujme druhou rovnici a dosadíme do ní nalezený výraz:

Uvažujme první rovnici a dosaďte nalezené výrazy a do ní:

Ano, kalkulačka, která počítá běžné zlomky, je stále pohodlná.

Takže obecné řešení je:

Ještě jednou, jak to dopadlo? Volná proměnná je sama na svém oprávněném čtvrtém místě. Výsledné výrazy pro základní proměnné zaujaly také svá pořadová místa.

Pojďme okamžitě zkontrolovat obecné řešení. Práce je pro černochy, ale už jsem to udělal, tak se toho chytněte =)

Do levé strany každé rovnice systému dosadíme tři hrdiny , :

Získají se odpovídající pravé strany rovnic, takže obecné řešení je nalezeno správně.

Nyní z nalezeného obecného řešení dostaneme dvě konkrétní řešení. Jedinou volnou proměnnou je zde kuchař. Není třeba si lámat hlavu.

Nechte to být – soukromé řešení.
Nechte to být – další soukromé řešení.

Odpovědět: Společné rozhodnutí: , soukromá řešení: , .

Neměl jsem si vzpomínat na černochy... ...protože se mi v hlavě vyrojily nejrůznější sadistické motivy a vzpomněl jsem si na slavný photoshop, ve kterém Ku Klux Klansmen v bílých hábitech běží po hřišti za černým fotbalistou. Sedím a tiše se usmívám. Víš, jak ruší...

Spousta matematiky škodí, takže podobný závěrečný příklad k vyřešení sám.

Příklad 6

Najděte obecné řešení soustavy lineárních rovnic.

Obecné řešení jsem již zkontroloval, odpověď lze věřit. Vaše řešení se může lišit od mého řešení, hlavní je, že obecná řešení se shodují.

Mnoho lidí si pravděpodobně všimlo nepříjemného momentu v řešeních: velmi často jsme si při obrácení Gaussovy metody museli pohrát s obyčejné zlomky. V praxi tomu tak skutečně je, případy, kdy žádné zlomky nejsou, jsou mnohem méně časté. Buďte připraveni psychicky a hlavně technicky.

Pozastavím se u některých vlastností řešení, které nebyly v řešených příkladech nalezeny.

Obecné řešení systému může někdy obsahovat konstantu (nebo konstanty), například: . Zde se jedna ze základních proměnných rovná konstantnímu číslu: . Na tom není nic exotického, to se stává. Je zřejmé, že v tomto případě bude každé konkrétní řešení obsahovat pětku na první pozici.

Zřídka, ale existují systémy, ve kterých počet rovnic je větší než počet proměnných. Gaussova metoda funguje v nejtěžších podmínkách, rozšířenou matici systému je třeba v klidu redukovat do stupňovité podoby pomocí standardního algoritmu. Takový systém může být nekonzistentní, může mít nekonečně mnoho řešení a kupodivu může mít jediné řešení.

Gaussova metoda, nazývaná také metoda sekvenční eliminace neznámých, je následující. Pomocí elementárních transformací je soustava lineárních rovnic uvedena do takové podoby, že její matice koeficientů se ukáže jako lichoběžníkový (stejný jako trojúhelníkový nebo stupňovitý) nebo blízko lichoběžníkovému (přímý tah Gaussovy metody, dále - jednoduše přímý tah). Příklad takového systému a jeho řešení je na obrázku výše.

V takovém systému poslední rovnice obsahuje pouze jednu proměnnou a její hodnotu lze jednoznačně zjistit. Hodnota této proměnné se pak dosadí do předchozí rovnice ( inverzní ke Gaussově metodě , pak jen obráceně), ze které je nalezena předchozí proměnná a tak dále.

V lichoběžníkovém (trojúhelníkovém) systému, jak vidíme, třetí rovnice již neobsahuje proměnné y A X a druhá rovnice je proměnná X .

Poté, co matice systému nabyla lichoběžníkového tvaru, již není těžké porozumět problematice kompatibility systému, určit počet řešení a najít řešení samotná.

Výhody metody:

1. při řešení soustav lineárních rovnic s více než třemi rovnicemi a neznámými není Gaussova metoda tak těžkopádná jako Cramerova metoda, protože řešení Gaussovou metodou vyžaduje méně výpočtů;
2. Gaussova metoda dokáže řešit neurčité soustavy lineárních rovnic, tedy takové, které mají obecné řešení (a ty si v této lekci rozebereme) a pomocí Cramerovy metody můžeme pouze konstatovat, že soustava je neurčitá;
3. můžete řešit soustavy lineárních rovnic, ve kterých počet neznámých není roven počtu rovnic (v této lekci je také rozebereme);
4. Metoda je založena na elementárních (školních) metodách - metodě dosazování neznámých a metodě sčítání rovnic, kterých jsme se dotkli v odpovídajícím článku.

Aby každý pochopil jednoduchost, s jakou se řeší lichoběžníkové (trojúhelníkové, stupňovité) soustavy lineárních rovnic, uvádíme řešení takové soustavy pomocí zpětného pohybu. Rychlé rozhodnutí Tento systém byl znázorněn na obrázku na začátku lekce.

Příklad 1 Vyřešte soustavu lineárních rovnic pomocí inverze:

Řešení. V tomto lichoběžníkovém systému proměnná z lze jednoznačně nalézt ze třetí rovnice. Její hodnotu dosadíme do druhé rovnice a získáme hodnotu proměnné y:

Nyní známe hodnoty dvou proměnných - z A y. Dosadíme je do první rovnice a získáme hodnotu proměnné X:

Z předchozích kroků vypíšeme řešení soustavy rovnic:

Pro získání takovéto lichoběžníkové soustavy lineárních rovnic, kterou jsme řešili velmi jednoduše, je nutné použít dopředný zdvih spojený s elementárními transformacemi soustavy lineárních rovnic. Taky to není moc těžké.

Elementární transformace soustavy lineárních rovnic

Opakováním školní metody algebraického sčítání rovnic soustavy jsme zjistili, že k jedné z rovnic soustavy můžeme přidat další rovnici soustavy a každou z rovnic lze vynásobit nějakými čísly. Výsledkem je soustava lineárních rovnic ekvivalentní této soustavě. V něm již jedna rovnice obsahovala pouze jednu proměnnou, jejíž dosazením hodnoty do jiných rovnic dojdeme k řešení. Takové přidání je jedním z typů elementární transformace systému. Při použití Gaussovy metody můžeme použít několik typů transformací.

Animace výše ukazuje, jak se soustava rovnic postupně mění v lichoběžníkovou. Tedy ten, který jste viděli v úplně první animaci a přesvědčili se, že je snadné v něm najít hodnoty všech neznámých. Jak takovou transformaci provést a samozřejmě příklady budou diskutovány dále.

Při řešení soustav lineárních rovnic s libovolným počtem rovnic a neznámých v soustavě rovnic a v rozšířené matici soustavy Umět:

1. přeuspořádat řádky (to bylo zmíněno na samém začátku tohoto článku);
2. pokud jiné transformace vedou ke stejným nebo proporcionálním řádkům, lze je smazat, s výjimkou jednoho;
3. odstranit „nulové“ řádky, kde jsou všechny koeficienty rovny nule;
4. vynásobte nebo vydělte libovolný řetězec určitým číslem;
5. k libovolnému řádku přidejte další řádek, vynásobený určitým číslem.

Výsledkem transformací je soustava lineárních rovnic ekvivalentní této soustavě.

Algoritmus a příklady řešení soustavy lineárních rovnic se čtvercovou maticí soustavy pomocí Gaussovy metody

Uvažujme nejprve řešení soustav lineárních rovnic, ve kterých je počet neznámých roven počtu rovnic. Matice takového systému je čtvercová, to znamená, že počet řádků v ní se rovná počtu sloupců.

Příklad 2Řešte soustavu lineárních rovnic pomocí Gaussovy metody

Při řešení soustav lineárních rovnic školními metodami jsme jednu z rovnic člen po členu násobili určitým číslem, takže koeficienty první proměnné v obou rovnicích byla opačná čísla. Při sčítání rovnic tato proměnná odpadá. Podobně funguje Gaussova metoda.

Pro zjednodušení vzhledřešení pojďme vytvořit rozšířenou matici systému:

V této matici jsou koeficienty neznámých umístěny vlevo před svislou čarou a volné členy jsou umístěny vpravo za svislou čarou.

Pro usnadnění dělení koeficientů pro proměnné (pro získání dělení jednotkou) Prohodíme první a druhý řádek systémové matice. Získáme systém ekvivalentní tomuto, protože v systému lineárních rovnic lze rovnice zaměňovat:

Pomocí nové první rovnice odstranit proměnnou X z druhé a všech následujících rovnic. K tomu přidáme do druhého řádku matice první řádek vynásobený (v našem případě ), do třetího řádku - první řádek vynásobený (v našem případě ).

To je možné, protože

Kdyby naše soustava rovnic měla více než tři, pak by bylo nutné do všech následujících rovnic přidat první řádek, vynásobený poměrem odpovídajících koeficientů, braný se znaménkem mínus.

V důsledku toho získáme matici ekvivalentní tomuto systému nový systém rovnice, ve kterých jsou všechny rovnice, počínaje druhým neobsahují proměnnou X :

Pro zjednodušení druhého řádku výsledného systému jej vynásobte a znovu získáte matici soustavy rovnic ekvivalentní této soustavě:

Nyní ponecháme první rovnici výsledného systému nezměněnou, pomocí druhé rovnice eliminujeme proměnnou y ze všech následujících rovnic. K tomu přidáme ke třetímu řádku systémové matice druhý řádek, vynásobený (v našem případě ).

Pokud by v našem systému bylo více než tři rovnice, pak bychom ke všem následujícím rovnicím museli přidat druhý řádek, vynásobený poměrem odpovídajících koeficientů braných se znaménkem mínus.

Výsledkem je, že opět získáme matici systému ekvivalentního tomuto systému lineárních rovnic:

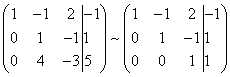
Získali jsme ekvivalentní lichoběžníkový systém lineárních rovnic:

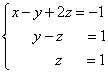
Pokud je počet rovnic a proměnných větší než v našem příkladu, pak proces postupného odstraňování proměnných pokračuje, dokud se matice systému nestane lichoběžníkovým, jako v našem ukázkovém příkladu.

Najdeme řešení „od konce“ - zpětný pohyb. Pro tohle z poslední rovnice určíme z:
.
Dosazením této hodnoty do předchozí rovnice najdeme y:

Z první rovnice najdeme X:

Odpověď: řešení této soustavy rovnic je .

: v tomto případě bude dána stejná odpověď, pokud má systém jedinečné řešení. Pokud má systém nekonečný počet řešení, pak toto bude odpověď a to je předmětem páté části této lekce.

Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody sami a pak se podívejte na řešení

Opět zde máme příklad konzistentního a určitého systému lineárních rovnic, ve kterém je počet rovnic roven počtu neznámých. Rozdíl oproti našemu ukázkovému příkladu z algoritmu je ten, že již existují čtyři rovnice a čtyři neznámé.

Příklad 4. Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody:

Nyní musíte použít druhou rovnici k odstranění proměnné z následujících rovnic. Pojďme provést přípravné práce. Aby to bylo s poměrem koeficientů pohodlnější, musíte jeden dostat do druhého sloupce druhého řádku. Chcete-li to provést, odečtěte třetí od druhého řádku a výsledný druhý řádek vynásobte -1.

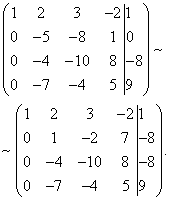
Proveďme nyní vlastní eliminaci proměnné ze třetí a čtvrté rovnice. Chcete-li to provést, přidejte druhý řádek, vynásobený , ke třetímu řádku a druhý, násobený , ke čtvrtému řádku.

Nyní pomocí třetí rovnice odstraníme proměnnou ze čtvrté rovnice. Chcete-li to provést, přidejte třetí řádek ke čtvrtému řádku, vynásobený . Získáme rozšířenou lichoběžníkovou matrici.

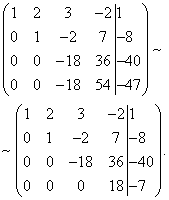
Získali jsme soustavu rovnic, kterým je daná soustava ekvivalentní:

Výsledné a dané systémy jsou tedy kompatibilní a jednoznačné. Konečné rozhodnutí najdeme „od konce“. Ze čtvrté rovnice můžeme přímo vyjádřit hodnotu proměnné „x-čtyři“:

Tuto hodnotu dosadíme do třetí rovnice soustavy a dostaneme

,

,

Nakonec substituce hodnot

První rovnice dává

,

kde najdeme „x první“:

Odpověď: tato soustava rovnic má jedinečné řešení .

Řešení systému můžete také zkontrolovat na kalkulačce Cramerovou metodou: v tomto případě bude stejná odpověď poskytnuta, pokud má systém jedinečné řešení.

Řešení aplikovaných úloh pomocí Gaussovy metody na příkladu úlohy na slitinách

Systémy lineárních rovnic se používají k modelování reálných objektů ve fyzickém světě. Pojďme vyřešit jeden z těchto problémů - slitiny. Podobné problémy - problémy na směsích, náklady popř specifická gravitace jednotlivé zboží ve skupině produktů a podobně.

Příklad 5. Tři kusy slitiny mají celkovou hmotnost 150 kg. První slitina obsahuje 60% mědi, druhá - 30%, třetí - 10%. Navíc ve druhé a třetí slitině dohromady je o 28,4 kg mědi méně než v první slitině a ve třetí slitině je o 6,2 kg méně mědi než ve druhé. Najděte hmotnost každého kusu slitiny.

Řešení. Sestavíme soustavu lineárních rovnic:

Vynásobíme druhou a třetí rovnici 10, získáme ekvivalentní systém lineárních rovnic:

Vytvoříme rozšířenou matici systému:

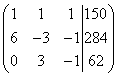
Pozor, přímo vpřed. Přičtením (v našem případě odečtením) jednoho řádku vynásobeného číslem (aplikujeme dvakrát) dochází s rozšířenou maticí systému k následujícím transformacím:

Přímý tah je u konce. Získali jsme expandovanou lichoběžníkovou matrici.

Aplikujeme zpětný pohyb. Najdeme řešení od konce. To vidíme.

Z druhé rovnice zjistíme

Ze třetí rovnice -

Řešení systému můžete také zkontrolovat na kalkulačce Cramerovou metodou: v tomto případě bude stejná odpověď poskytnuta, pokud má systém jedinečné řešení.

O jednoduchosti Gaussovy metody svědčí i to, že německému matematikovi Carlu Friedrichu Gaussovi trvalo její vynalezení pouhých 15 minut. Kromě po něm pojmenované metody je z Gaussových děl známé rčení „Neměli bychom zaměňovat to, co se nám zdá neuvěřitelné a nepřirozené, s naprosto nemožným“ – jakýsi druh stručné pokyny dělat objevy.

V mnoha aplikovaných úlohách nemusí existovat třetí omezení, tedy třetí rovnice, pak musíte řešit soustavu dvou rovnic o třech neznámých pomocí Gaussovy metody, nebo naopak neznámých je méně než rovnic. Nyní začneme takové soustavy rovnic řešit.

Pomocí Gaussovy metody můžete určit, zda je některý systém kompatibilní nebo nekompatibilní n lineární rovnice s n proměnné.

Gaussova metoda a soustavy lineárních rovnic s nekonečným počtem řešení

Dalším příkladem je konzistentní, ale neurčitý systém lineárních rovnic, to znamená, že má nekonečný počet řešení.

Po provedení transformací v rozšířené matici systému (přeuspořádání řádků, násobení a dělení řádků určitým číslem, přidání dalšího k jednomu řádku) se mohly objevit řádky formuláře

Pokud ve všech rovnicích majících tvar

Volné členy se rovnají nule, to znamená, že systém je neurčitý, to znamená, že má nekonečně mnoho řešení a rovnice tohoto typu jsou „nadbytečné“ a ze systému je vyřazujeme.

Příklad 6.

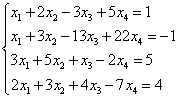
Řešení. Vytvořme rozšířenou matici systému. Potom pomocí první rovnice odstraníme proměnnou z následujících rovnic. Chcete-li to provést, přidejte do druhého, třetího a čtvrtého řádku první, vynásobený:

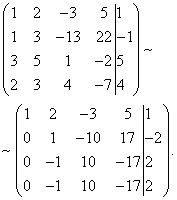
Nyní přidáme druhý řádek ke třetímu a čtvrtému.

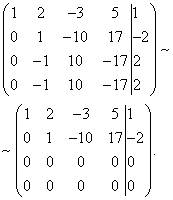
V důsledku toho se dostáváme k systému

Poslední dvě rovnice se změnily na rovnice tvaru. Tyto rovnice jsou splněny pro jakoukoli hodnotu neznámých a lze je vyřadit.

Abychom splnili druhou rovnici, můžeme zvolit libovolné hodnoty pro a , pak bude hodnota pro určena jednoznačně: . Z první rovnice je hodnota pro také nalezena jednoznačně: .

Daný i poslední systém jsou konzistentní, ale nejisté, a vzorce

pro libovolné a dejte nám všechna řešení daného systému.

Gaussova metoda a soustavy lineárních rovnic bez řešení

Dalším příkladem je nekonzistentní systém lineárních rovnic, tedy takový, který nemá řešení. Odpověď na takové problémy je formulována takto: systém nemá řešení.

Jak již bylo zmíněno v souvislosti s prvním příkladem, po provedení transformací se v rozšířené matici systému mohly objevit řádky formuláře

odpovídající rovnici tvaru

Pokud mezi nimi existuje alespoň jedna rovnice s nenulovým volným členem (tj. ), pak je tato soustava rovnic nekonzistentní, to znamená, že nemá řešení a její řešení je úplné.

Příklad 7. Vyřešte soustavu lineárních rovnic pomocí Gaussovy metody:

Řešení. Sestavíme rozšířenou matici systému. Pomocí první rovnice vyloučíme proměnnou z následujících rovnic. Chcete-li to provést, přidejte první řádek vynásobený druhým řádkem, první řádek vynásobený třetím řádkem a první řádek vynásobený čtvrtým řádkem.

Nyní musíte použít druhou rovnici k odstranění proměnné z následujících rovnic. Abychom získali celočíselné poměry koeficientů, prohodíme druhý a třetí řádek rozšířené matice systému.

Chcete-li vyloučit třetí a čtvrtou rovnici, přidejte druhou vynásobenou , na třetí řádek a druhou násobenou , do čtvrtého řádku.

Nyní pomocí třetí rovnice odstraníme proměnnou ze čtvrté rovnice. Chcete-li to provést, přidejte třetí řádek ke čtvrtému řádku, vynásobený .

Daný systém je tedy ekvivalentní následujícímu:

Výsledný systém je nekonzistentní, protože jeho poslední rovnice nemůže být splněna žádnými hodnotami neznámých. Proto tento systém nemá řešení.

Obsah lekce

Lineární rovnice ve dvou proměnných

Školák má 200 rublů na oběd ve škole. Dort stojí 25 rublů a šálek kávy stojí 10 rublů. Kolik dortů a šálků kávy si můžete koupit za 200 rublů?

Označme počet dortů podle X a počet prolitých šálků kávy y. Potom bude cena dortů označena výrazem 25 X a náklady na šálky kávy za 10 y .

25X- cena X koláče
10y — cena yšálky kávy

Celková částka by měla být 200 rublů. Pak dostaneme rovnici se dvěma proměnnými X A y

25X+ 10y= 200

Kolik kořenů má tato rovnice?

Vše závisí na chuti studenta. Pokud si koupí 6 dortů a 5 šálků kávy, pak kořeny rovnice budou čísla 6 a 5.

Dvojice hodnot 6 a 5 jsou považovány za kořeny rovnice 25 X+ 10y= 200. Zapsáno jako (6; 5), přičemž první číslo je hodnota proměnné X a druhá - hodnota proměnné y .

6 a 5 nejsou jediné kořeny, které obracejí rovnici 25 X+ 10y= 200 k identitě. Pokud je to žádoucí, za stejných 200 rublů si student může koupit 4 koláče a 10 šálků kávy:

V tomto případě kořeny rovnice 25 X+ 10y= 200 je dvojice hodnot (4; 10).

Školák si navíc nemusí kupovat kávu vůbec, ale kupovat dorty za celých 200 rublů. Pak kořeny rovnice 25 X+ 10y= 200 budou hodnoty 8 a 0

Nebo naopak, nekupujte dorty, ale kupujte kávu za celých 200 rublů. Pak kořeny rovnice 25 X+ 10y= 200, hodnoty budou 0 a 20

Zkusme vyjmenovat všechny možné kořeny rovnice 25 X+ 10y= 200. Shodněme se, že hodnoty X A y patří do množiny celých čísel. A nechť jsou tyto hodnoty větší nebo rovné nule:

X∈Z y∈ Z;
x ≥ 0, y ≥ 0

To bude výhodné pro samotného studenta. Je výhodnější koupit celé dorty než například několik celých dortů a půl dortu. Je také pohodlnější brát kávu v celých šálcích než například několik celých šálků a půl šálku.

Všimněte si, že pro liché X za žádných okolností není možné dosáhnout rovnosti y. Pak hodnoty X následující čísla budou 0, 2, 4, 6, 8. A vědět X lze snadno určit y

Získali jsme tedy následující dvojice hodnot (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Tyto dvojice jsou řešeními nebo kořeny rovnice 25 X+ 10y= 200. Udělají z této rovnice identitu.

Rovnice formuláře ax + by = c volal lineární rovnice se dvěma proměnnými. Řešením nebo kořeny této rovnice je dvojice hodnot ( X; y), která ji promění v identitu.

Všimněte si také, že pokud je lineární rovnice se dvěma proměnnými zapsána ve tvaru ax + b y = c , pak říkají, že je to napsané kanonický(normální) forma.

Některé lineární rovnice ve dvou proměnných lze redukovat na kanonickou formu.

Například rovnice 2(16X+ 3y − 4) = 2(12 + 8X − y) lze připomenout ax + by = c. Otevřeme závorky na obou stranách této rovnice a dostaneme 32X + 6y − 8 = 24 + 16X − 2y . Seskupujeme členy obsahující neznámé na levé straně rovnice a členy bez neznámých - na pravé straně. Pak dostaneme 32x− 16X+ 6y+ 2y = 24 + 8 . Uvedeme podobné členy na obou stranách, dostaneme rovnici 16 X+ 8y= 32. Tato rovnice je redukována do tvaru ax + by = c a je kanonický.

Rovnice 25 diskutovaná dříve X+ 10y= 200 je také lineární rovnice se dvěma proměnnými v kanonickém tvaru. V této rovnici parametry A , b A C se rovnají hodnotám 25, 10 a 200.

Vlastně rovnice ax + by = c má nespočet řešení. Řešení rovnice 25X+ 10y= 200, jeho kořeny jsme hledali pouze na množině celých čísel. V důsledku toho jsme získali několik párů hodnot, které tuto rovnici proměnily v identitu. Ale na mnoha racionální čísla rovnice 25 X+ 10y= 200 bude mít nekonečně mnoho řešení.

Chcete-li získat nové páry hodnot, musíte použít libovolnou hodnotu pro X, pak se vyjádři y. Vezměme si například proměnnou X hodnota 7. Pak dostaneme rovnici s jednou proměnnou 25×7 + 10y= 200 ve kterém se dá vyjádřit y

Nechat X= 15. Pak rovnice 25X+ 10y= 200 se změní na 25 × 15 + 10y= 200. Odtud to zjistíme y = −17,5

Nechat X= -3. Pak rovnice 25X+ 10y= 200 se změní na 25 × (-3) + 10y= 200. Odtud to zjistíme y = −27,5

Soustava dvou lineárních rovnic se dvěma proměnnými

Pro rovnici ax + by = c můžete vzít libovolné hodnoty, kolikrát chcete X a najít hodnoty pro y. Vzato samostatně, bude mít taková rovnice nespočet řešení.

Ale také se stává, že proměnné X A y spojené ne jednou, ale dvěma rovnicemi. V tomto případě tvoří tzv soustava lineárních rovnic ve dvou proměnných. Takový systém rovnic může mít jeden pár hodnot (nebo jinými slovy: „jedno řešení“).

Může se také stát, že systém nemá vůbec žádná řešení. Systém lineárních rovnic může mít ve vzácných a výjimečných případech nespočet řešení.

Dvě lineární rovnice tvoří systém, kdy hodnoty X A y zadejte do každé z těchto rovnic.

Vraťme se k úplně první rovnici 25 X+ 10y= 200. Jednou z dvojic hodnot pro tuto rovnici byla dvojice (6; 5) . To je případ, kdy si za 200 rublů můžete koupit 6 dortů a 5 šálků kávy.

Formulujme úlohu tak, aby se dvojice (6; 5) stala jediným řešením rovnice 25 X+ 10y= 200. Chcete-li to provést, vytvořte další rovnici, která by spojovala totéž X koláče a yšálky kávy.

Uveďme text problému takto:

„Student koupil několik dortů a několik šálků kávy za 200 rublů. Dort stojí 25 rublů a šálek kávy stojí 10 rublů. Kolik dortů a šálků kávy si student koupil, pokud je známo, že počet dortů je o jednotku větší než počet šálků kávy?

První rovnici už máme. Toto je rovnice 25 X+ 10y= 200. Nyní vytvoříme rovnici pro podmínku „počet dortů je o jednotku větší než počet šálků kávy“ .

Počet dortů je X, a počet šálků kávy je y. Tuto frázi můžete napsat pomocí rovnice x-y= 1. Tato rovnice bude znamenat, že rozdíl mezi dorty a kávou je 1.

x = y+ 1. Tato rovnice znamená, že počet dortů je o jeden větší než počet šálků kávy. Pro dosažení rovnosti se k počtu šálků kávy přidá jedna. To lze snadno pochopit, pokud použijeme model měřítek, který jsme uvažovali při studiu nejjednodušších problémů:

Máme dvě rovnice: 25 X+ 10y= 200 a x = y+ 1. Vzhledem k tomu, že hodnoty X A y, konkrétně 6 a 5 jsou zahrnuty v každé z těchto rovnic, pak dohromady tvoří systém. Pojďme si tento systém zapsat. Pokud rovnice tvoří systém, pak jsou orámovány znakem systému. Symbol systému je složená závorka:

Pojďme se rozhodnout tento systém. To nám umožní vidět, jak se dostáváme k hodnotám 6 a 5. Existuje mnoho metod pro řešení takových systémů. Podívejme se na nejoblíbenější z nich.

Substituční metoda

Název této metody mluví sám za sebe. Její podstatou je dosazení jedné rovnice do druhé, která předtím vyjádřila jednu z proměnných.

V našem systému není třeba nic vyjadřovat. Ve druhé rovnici X = y+ 1 proměnná X již vyjádřeno. Tato proměnná se rovná výrazu y+ 1. Pak můžete tento výraz dosadit do první rovnice místo proměnné X

Po dosazení výrazu y+ 1 do první rovnice místo toho X, dostaneme rovnici 25(y+ 1) + 10y= 200 . Toto je lineární rovnice s jednou proměnnou. Tato rovnice je poměrně snadno řešitelná:

Zjistili jsme hodnotu proměnné y. Nyní dosadíme tuto hodnotu do jedné z rovnic a najdeme hodnotu X. K tomu je vhodné použít druhou rovnici X = y+ 1. Dosadíme do něj hodnotu y

To znamená, že dvojice (6; 5) je řešením soustavy rovnic, jak jsme zamýšleli. Zkontrolujeme a ujistíme se, že dvojice (6; 5) vyhovuje systému:

Příklad 2

Dosadíme první rovnici X= 2 + y do druhé rovnice 3 x− 2y= 9. V první rovnici proměnná X rovná se výrazu 2 + y. Dosadíme tento výraz do druhé rovnice místo X

Nyní najdeme hodnotu X. Chcete-li to provést, dosaďte hodnotu y do první rovnice X= 2 + y

To znamená, že řešením systému je párová hodnota (5; 3)

Příklad 3. Řešit substitucí následující systém rovnice:

Zde na rozdíl od předchozích příkladů není jedna z proměnných vyjádřena explicitně.

Chcete-li nahradit jednu rovnici jinou, musíte nejprve .

Je vhodné vyjádřit proměnnou, která má koeficient jedna. Proměnná má koeficient jedna X, který je obsažen v první rovnici X+ 2y= 11. Vyjádřeme tuto proměnnou.

Po proměnné výraz X, náš systém bude mít následující podobu:

Nyní dosadíme první rovnici do druhé a najdeme hodnotu y

Pojďme nahradit y X

To znamená, že řešením systému je dvojice hodnot (3; 4)

Samozřejmě můžete vyjádřit i proměnnou y. Tím se nezmění kořeny. Ale pokud se vyjádříte y, Výsledkem není příliš jednoduchá rovnice, jejíž řešení zabere více času. Bude to vypadat takto:

Vidíme, že v tomto příkladu vyjadřujeme X mnohem pohodlnější než vyjádření y .

Příklad 4. Vyřešte následující soustavu rovnic pomocí substituční metody:

Vyjádřeme se v první rovnici X. Poté bude mít systém podobu:

y

Pojďme nahradit y do první rovnice a najděte X. Můžete použít původní rovnici 7 X+ 9y= 8, nebo použijte rovnici, ve které je proměnná vyjádřena X. Použijeme tuto rovnici, protože je vhodná:

To znamená, že řešením systému je dvojice hodnot (5; −3)

Způsob sčítání

Metoda sčítání spočívá v přidávání rovnic zahrnutých v systému po členech. Výsledkem tohoto přidání je nová rovnice s jednou proměnnou. A řešení takové rovnice je celkem jednoduché.

Pojďme vyřešit následující soustavu rovnic:

Přidejme levou stranu první rovnice k levé straně druhé rovnice. A pravá strana první rovnice s pravá strana druhá rovnice. Dostaneme následující rovnost:

Podívejme se na podobné pojmy:

Ve výsledku jsme dostali nejjednodušší rovnici 3 X= 27, jehož kořen je 9. Znát hodnotu X můžete najít hodnotu y. Dosadíme hodnotu X do druhé rovnice x-y= 3. Dostáváme 9 − y= 3. Odtud y= 6 .

To znamená, že řešením systému je dvojice hodnot (9; 6)

Příklad 2

Přidejme levou stranu první rovnice k levé straně druhé rovnice. A pravá strana první rovnice s pravou stranou druhé rovnice. Ve výsledné rovnosti uvádíme podobné pojmy:

Ve výsledku jsme dostali nejjednodušší rovnici 5 X= 20, jehož kořen je 4. Znát hodnotu X můžete najít hodnotu y. Dosadíme hodnotu X do první rovnice 2 x+y= 11. Dáme 8+ y= 11. Odtud y= 3 .

To znamená, že řešením systému je dvojice hodnot (4;3)

Proces přidávání není podrobně popsán. Musí se to zvládnout psychicky. Při sčítání je třeba obě rovnice zredukovat na kanonickou formu. To je mimochodem ac + by = c .

Z uvažovaných příkladů je zřejmé, že hlavním účelem sčítání rovnic je zbavit se jedné z proměnných. Ale ne vždy je možné okamžitě vyřešit soustavu rovnic metodou sčítání. Nejčastěji je systém nejprve uveden do formy, ve které lze přidat rovnice obsažené v tomto systému.

Například systém lze řešit ihned přidáním. Při sečtení obou rovnic jsou členy y A −y zmizí, protože jejich součet je nula. V důsledku toho je vytvořena nejjednodušší rovnice 11 X= 22, jehož kořen je 2. Poté bude možné určit y rovný 5.

A soustava rovnic Metodu sčítání nelze vyřešit okamžitě, protože to nepovede ke zmizení jedné z proměnných. Sečtením vznikne rovnice 8 X+ y= 28, který má nekonečný počet řešení.

Pokud se obě strany rovnice vynásobí nebo vydělí stejným číslem, které se nerovná nule, dostanete rovnici ekvivalentní dané jedničce. Toto pravidlo platí i pro soustavu lineárních rovnic se dvěma proměnnými. Jednu z rovnic (nebo obě rovnice) lze vynásobit libovolným číslem. Výsledkem bude ekvivalentní systém, jehož kořeny se budou shodovat s předchozím.

Vraťme se k úplně prvnímu systému, který popisoval, kolik dortů a šálků kávy si školák koupil. Řešením tohoto systému byla dvojice hodnot (6; 5).

Vynásobme obě rovnice obsažené v této soustavě nějakými čísly. Řekněme, že vynásobíme první rovnici 2 a druhou 3

V důsledku toho jsme získali systém
Řešením tohoto systému je stále dvojice hodnot (6; 5)

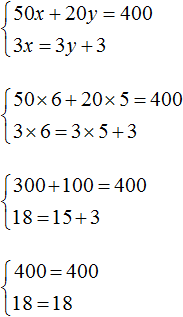
To znamená, že rovnice obsažené v systému lze zredukovat na formu vhodnou pro aplikaci sčítací metody.

Vraťme se k systému , kterou jsme nedokázali vyřešit pomocí sčítací metody.

Vynásobte první rovnici 6 a druhou −2

Pak dostaneme následující systém:

Sečtěte rovnice obsažené v této soustavě. Přidání komponent 12 X a -12 X výsledkem bude 0, sčítání 18 y a 4 y dá 22 y a sečtením 108 a −20 dostaneme 88. Pak dostaneme rovnici 22 y= 88, odtud y = 4 .

Pokud je zpočátku těžké sečíst rovnice v hlavě, můžete si napsat, jak se to sčítá levá strana první rovnice s levou stranou druhé rovnice a pravá strana první rovnice s pravou stranou druhé rovnice:

S vědomím, že hodnota proměnné y rovná se 4, můžete najít hodnotu X. Pojďme nahradit y do jedné z rovnic, například do první rovnice 2 X+ 3y= 18. Pak dostaneme rovnici s jednou proměnnou 2 X+ 12 = 18. Přesuneme 12 na pravou stranu a změníme znaménko, dostaneme 2 X= 6, odtud X = 3 .

Příklad 4. Vyřešte následující soustavu rovnic metodou sčítání:

Vynásobme druhou rovnici −1. Poté bude mít systém následující podobu:

Sečteme obě rovnice. Přidávání komponent X A −x výsledkem bude 0, sčítání 5 y a 3 y dá 8 y a sečtením 7 a 1 dostaneme 8. Výsledkem je rovnice 8 y= 8, jehož kořen je 1. S vědomím, že hodnota y rovná se 1, můžete najít hodnotu X .

Pojďme nahradit y do první rovnice, dostaneme X+ 5 = 7, tedy X= 2

Příklad 5. Vyřešte následující soustavu rovnic metodou sčítání:

Je žádoucí, aby termíny obsahující stejné proměnné byly umístěny pod sebou. Proto ve druhé rovnici platí členy 5 y a -2 X Pojďme si vyměnit místa. V důsledku toho bude mít systém podobu:

Vynásobme druhou rovnici 3. Pak bude systém mít tvar:

Nyní sečteme obě rovnice. Výsledkem sčítání dostaneme rovnici 8 y= 16, jehož kořen je 2.

Pojďme nahradit y do první rovnice dostaneme 6 X− 14 = 40. Posuňme člen −14 na pravou stranu, změníme znaménko, a dostaneme 6 X= 54. Odtud X= 9.

Příklad 6. Vyřešte následující soustavu rovnic metodou sčítání:

Zbavme se zlomků. Vynásobte první rovnici 36 a druhou 12

Ve výsledném systému první rovnici lze vynásobit −5 a druhou 8

Sečteme rovnice ve výsledné soustavě. Pak dostaneme nejjednodušší rovnici −13 y= -156. Odtud y= 12. Pojďme nahradit y do první rovnice a najděte X

Příklad 7. Vyřešte následující soustavu rovnic metodou sčítání:

Uveďme obě rovnice do normálního tvaru. Zde je vhodné použít pravidlo proporce v obou rovnicích. Pokud je v první rovnici pravá strana reprezentována jako a pravá strana druhé rovnice jako , pak bude mít systém tvar:

Máme poměr. Vynásobme její extrémní a střední pojmy. Poté bude mít systém podobu:

Vynásobme první rovnici −3 a otevřeme závorky ve druhé:

Nyní sečteme obě rovnice. V důsledku sečtení těchto rovnic dostaneme rovnost s nulou na obou stranách:

Ukazuje se, že systém má nespočet řešení.

Ale nemůžeme si jen tak vzít libovolné hodnoty z nebe X A y. Můžeme zadat jednu z hodnot a druhá bude určena v závislosti na hodnotě, kterou určíme. Například ať X= 2. Dosadíme tuto hodnotu do systému:

Výsledkem řešení jedné z rovnic je hodnota pro y, který splní obě rovnice:

Výsledná dvojice hodnot (2; −2) uspokojí systém:

Pojďme najít další pár hodnot. Nechat X= 4. Dosadíme tuto hodnotu do systému:

Hodnotu poznáte pouhým okem y rovná se nule. Pak dostaneme dvojici hodnot (4; 0), která vyhovuje našemu systému:

Příklad 8. Vyřešte následující soustavu rovnic metodou sčítání:

Vynásobte první rovnici 6 a druhou 12

Přepišme, co zbylo:

Vynásobme první rovnici −1. Poté bude mít systém podobu:

Nyní sečteme obě rovnice. V důsledku sčítání se vytvoří rovnice 6 b= 48, jehož kořen je 8. Dosaz b do první rovnice a najděte A

Systém lineárních rovnic se třemi proměnnými

Lineární rovnice se třemi proměnnými zahrnuje tři proměnné s koeficienty, stejně jako intercept term. V kanonické formě to může být zapsáno takto:

ax + by + cz = d

Tato rovnice má nespočet řešení. Zadáním dvou proměnných různých hodnot lze nalézt třetí hodnotu. Řešením je v tomto případě trojice hodnot ( X; y; z), který změní rovnici na identitu.

Pokud proměnné x, y, z jsou propojeny třemi rovnicemi, pak vzniká soustava tří lineárních rovnic se třemi proměnnými. K řešení takového systému můžete použít stejné metody, které platí pro lineární rovnice se dvěma proměnnými: substituční metodu a metodu sčítání.

Příklad 1. Vyřešte následující soustavu rovnic pomocí substituční metody:

Vyjádřeme se ve třetí rovnici X. Poté bude mít systém podobu:

Nyní provedeme substituci. Variabilní X se rovná výrazu 3 − 2y − 2z . Dosadíme tento výraz do první a druhé rovnice:

Otevřeme závorky v obou rovnicích a představíme podobné pojmy:

Dospěli jsme k soustavě lineárních rovnic se dvěma proměnnými. V tomto případě je vhodné použít metodu sčítání. V důsledku toho proměnná y zmizí a můžeme najít hodnotu proměnné z

Nyní najdeme hodnotu y. K tomu je vhodné použít rovnici − y+ z= 4. Dosaďte do něj hodnotu z

Nyní najdeme hodnotu X. K tomu je vhodné použít rovnici X= 3 − 2y − 2z . Dosadíme do něj hodnoty y A z

Trojice hodnot (3; −2; 2) je tedy řešením našeho systému. Kontrolou se ujistíme, že tyto hodnoty vyhovují systému:

Příklad 2. Soustavu řešte sčítací metodou

Sečteme první rovnici s druhou, vynásobíme −2.

Pokud se druhá rovnice vynásobí −2, dostane tvar −6X+ 6y − 4z = −4 . Nyní to přidáme k první rovnici:

Vidíme, že v důsledku elementárních transformací byla určena hodnota proměnné X. Rovná se jedné.

Vraťme se k hlavnímu systému. Sečtěme druhou rovnici s třetí, vynásobenou −1. Pokud se třetí rovnice vynásobí −1, dostane tvar −4X + 5y − 2z = −1 . Nyní to přidáme do druhé rovnice:

Dostali jsme rovnici x− 2y= -1. Dosadíme do něj hodnotu X které jsme našli dříve. Potom můžeme určit hodnotu y

Nyní známe významy X A y. To vám umožní určit hodnotu z. Použijme jednu z rovnic obsažených v systému:

Trojice hodnot (1; 1; 1) je tedy řešením našeho systému. Kontrolou se ujistíme, že tyto hodnoty vyhovují systému:

Problémy skládání soustav lineárních rovnic

Úloha skládání soustav rovnic je řešena zadáním několika proměnných. Dále jsou na základě podmínek úlohy sestaveny rovnice. Ze sestavených rovnic tvoří soustavu a řeší ji. Po vyřešení systému je nutné zkontrolovat, zda jeho řešení splňuje podmínky problému.

Problém 1. Z města do JZD vyjelo auto Volha. Vracela se zpět po jiné silnici, která byla o 5 km kratší než ta první. Celkem auto ujelo 35 km tam a zpět. Kolik kilometrů je dlouhá každá cesta?

Řešení

Nechat X- délka první cesty, y- délka druhého. Pokud auto ujelo 35 km tam a zpět, pak lze první rovnici napsat jako X+ y= 35. Tato rovnice popisuje součet délek obou cest.

Auto se prý vrátilo po silnici, která byla o 5 km kratší než ta první. Pak lze druhou rovnici zapsat jako X− y= 5. Tato rovnice ukazuje, že rozdíl mezi délkami silnic je 5 km.

Nebo lze druhou rovnici napsat jako X= y+ 5. Použijeme tuto rovnici.

Protože proměnné X A y v obou rovnicích označují stejné číslo, pak z nich můžeme sestavit systém:

Pojďme tento systém vyřešit pomocí některé z dříve studovaných metod. V tomto případě je vhodné použít substituční metodu, protože ve druhé rovnici proměnná X již vyjádřeno.

Dosaďte druhou rovnici do první a najděte y

Dosadíme nalezenou hodnotu y ve druhé rovnici X= y+ 5 a najdeme X

Délka první cesty byla určena pomocí proměnné X. Nyní jsme našli jeho význam. Variabilní X se rovná 20. To znamená, že délka první silnice je 20 km.

A délka druhé cesty byla označena y. Hodnota této proměnné je 15. To znamená, že délka druhé silnice je 15 km.

Pojďme zkontrolovat. Nejprve se ujistěte, že je systém správně vyřešen:

Nyní zkontrolujeme, zda řešení (20; 15) splňuje podmínky problému.

Auto prý ujelo celkem 35 km tam a zpět. Sečteme délky obou cest a dbáme na to, aby řešení (20; 15) vyhovovalo tento stav: 20 km + 15 km = 35 km

Následující podmínka: auto se vrátilo zpět po jiné silnici, která byla o 5 km kratší než ta první . Vidíme, že řešení (20; 15) také splňuje tuto podmínku, protože 15 km je kratší než 20 km o 5 km: 20 km − 15 km = 5 km

Při sestavování systému je důležité, aby proměnné reprezentovaly stejná čísla ve všech rovnicích obsažených v tomto systému.

Náš systém tedy obsahuje dvě rovnice. Tyto rovnice zase obsahují proměnné X A y, které představují v obou rovnicích stejná čísla, a to délky silnic 20 km a 15 km.

Problém 2. Na plošinu byly naloženy dubové a borovicové pražce, celkem 300 pražců. Je známo, že všechny dubové pražce vážily o 1 tunu méně než všechny borové pražce. Určete, kolik bylo zvlášť dubových a borových pražců, jestliže každý dubový pražec vážil 46 kg a každý borový 28 kg.

Řešení

Nechat X dub a y na plošinu byly naloženy borové pražce. Pokud by bylo celkem 300 pražců, pak lze první rovnici napsat jako x+y = 300 .

Všechny dubové pražce vážily 46 X kg a ty borové vážily 28 y kg. Protože dubové pražce vážily o 1 tunu méně než borové, lze druhou rovnici zapsat jako 28y − 46X= 1000 . Tato rovnice ukazuje, že rozdíl v hmotnosti mezi dubovými a borovicovými pražci je 1000 kg.

Tuny byly převedeny na kilogramy, protože hmotnost dubových a borových pražců byla měřena v kilogramech.

Výsledkem jsou dvě rovnice, které tvoří systém

Pojďme vyřešit tento systém. Vyjádřeme se v první rovnici X. Poté bude mít systém podobu:

Dosaďte první rovnici druhou a najděte y

Pojďme nahradit y do rovnice X= 300 − y a zjistit, co to je X

To znamená, že na plošinu bylo naloženo 100 dubových a 200 borových pražců.

Zkontrolujme, zda řešení (100; 200) splňuje podmínky úlohy. Nejprve se ujistěte, že je systém správně vyřešen:

Celkem prý bylo 300 pražců. Sečteme počet dubových a borovicových pražců a ujistíme se, že řešení (100; 200) splňuje tuto podmínku: 100 + 200 = 300.

Následující podmínka: všechny dubové pražce vážily o 1 tunu méně než všechny borové pražce . Vidíme, že řešení (100; 200) také splňuje tuto podmínku, protože 46 × 100 kg dubových pražců je lehčích než 28 × 200 kg borových pražců: 5600 kg − 4600 kg = 1000 kg.

Problém 3. Vzali jsme tři kusy slitiny mědi a niklu v hmotnostních poměrech 2: 1, 3: 1 a 5: 1. Vytavil se z nich kus o hmotnosti 12 kg s poměrem mědi a niklu 4:1. Najděte hmotnost každého původního kusu, pokud hmotnost prvního je dvojnásobkem hmotnosti druhého.